互联网金融风险度量模型选择研究
宋光辉,吴 超,吴 栩
(华南理工大学 工商管理学院,广东 广州 510640)
互联网金融风险度量模型选择研究
宋光辉,吴 超,吴 栩
(华南理工大学 工商管理学院,广东 广州 510640)
度量互联网金融风险非常重要,但传统的风险度量模型能否有效度量其风险,何种模型能更有效地度量其风险犹未可知。以余额宝的风险度量为例,分析了在90%和95%置信水平下的最优GARCH-VaR和GARCH-CVaR模型,作为对应置信水平下的VaR和CVaR的度量。结果表明,CVaR模型能更有效地度量互联网风险,其不仅可以很好地度量现有的风险水平,还对风险具有预测性。
互联网金融风险;GARCH模型;VaR;CVaR
一、问题的提出
2013年,余额宝拉开了互联网金融理财的序幕,带动了众多互联网企业在金融领域进行圈地运动,给传统的金融业带来前所未有的冲击。这些互联网理财产品凭借门槛低、流动性强、收益高的特点,迅速吸收了大量银行储蓄用户。尽管互联网金融较之传统金融,具有低成本、信息优势、高流动性、高收益等众多优势,但其仍面临着一些不容忽视的风险。而今,防范互联网金融风险的呼声已日益强烈。然而,防范互联网金融风险的前提在于对互联网金融风险进行度量;但遗憾的是,时至今日,学术界并没有统一的互联网金融风险度量模型,甚至空白。基于此,本文比较了传统的风险测度模型(Value atRisk,VaR)和(ConditionalValue atRisk,CVaR)在不同分布下对互联网金融的风险度量效果,研究两种模型在给定置信水平下的最优度量模型,根据两种模型对互联网金融风险度量的有效性进行模型选择,以期为互联网金融的风险管理提供有益参考。
二、方法介绍
(一)VaR与CVaR
1993年,G30集团在研究金融衍生品的基础上,首次提出了VaR方法,用来度量金融市场的风险,随后,VaR被金融界广泛采用。VaR方法可以全面地衡量包括利率风险、汇率风险、股票和商品价格风险以及金融衍生产品风险在内的各种市场风险,能够较为精确地计算交易风险的数值。VaR方法日益发展和普及,逐渐形成一个体系,成为金融风险管理的主流方法之一。然而,VaR方法本身也存在一定的局限性。事实上,Artzner(1997,1999)[1],Frittel(2002)[2],Giorgio(2002)[3]等的研究表明,一个行之有效的风险测量方法必须满足正齐性、次可加性、单调性和传递不变性,如果满足这些性质则称为一致性风险度量。而VaR在不服从正态分布的情况下不满足次可加性,即VaR不是一致性风险度量。
为了弥补VaR的缺陷,Rockafeller(2000,2001)[4-5]与Uryasev(1999,2000)[6]提出CVaR方法。CVaR测算的是在一定的置信水平下,损失超过VaR的潜在价值,或者是损失超过VaR的条件均值,代表了超额损失的平均水平,是一种有利于防范小概率极端金融风险的风险度量和优化工具[7]。根据CVaR的定义,用f(x,y)表示预期收益损失函数,x表示决策向量、代表金融资产的头寸或权重,y表示随机变量,代表对损失有影响的市场因素;则在给定置信度水平β下的CVaR可用如下(1)式表述
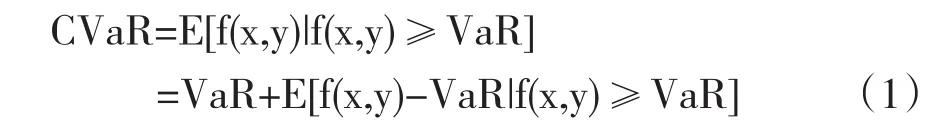
其中:f(x,y)是预期收益损失函数,x为决策向量,代表金融资产的头寸或权重,y是随机变量,代表对损失有影响的市场因素。
(二)GARCH模型
Bollerslev(1986)[8]在自回归条件异方差(Auto Regressive Conditional Heteroskedasticity,ARCH)模型的基础上提出了广义自回归条件异方差(GARCH)模型。GARCH模型有三种常见的分布形式:
(1)正态分布。正态分布的优点在于其具有对称性、可加性、相关性等容易测量的特点。但是简单正态分布存在缺陷,所以实际中多采用对数正态分布形式。(2)T分布。T分布的尾部要比标准正态分布厚,可以看成是广义的正态分布,但T分布缺乏正态分布良好的统计特征,而且多变量联合的T分布比较难估计。(3)广义误差(GED)分布。当GED分布的自由度(形状参数)为2时,其概率密度函数与标准正态分布的概率密度函数一致;当自由度小于2时,其有较正态分布更厚的尾部;当自由度大于2时,其尾部比正态分布的薄。一般GARCH模型的表现形式:

(2)式是均值方程,(3)式是条件方差方程。对于模型参数p,q的选取,本文采用AIC准则(Akaike information criterion),它可以权衡所估计模型的复杂度和此模型拟合数据的优良性,优先考虑的模型是AIC值最小的那一个。
(三)基于GARCH模型的VaR与CVaR计算
1.基于GARCH模型的VaR计算
我们可以利用GARCH族模型计算条件方差ht,进而可以得到相应的t时刻VaR的计算公式:

其中Pt-1表示滞后一期的资产价格,Z表示在给定置信水平α下的分位数。由公式(4)可得一个VaR序列,通过该序列既可以研究历史VaR值,也可以对未来VaR值进行预测。
2.基于GARCH模型的CVaR计算
根据CVaR的定义,可得基于GARCH模型的CVaR计算公式为:
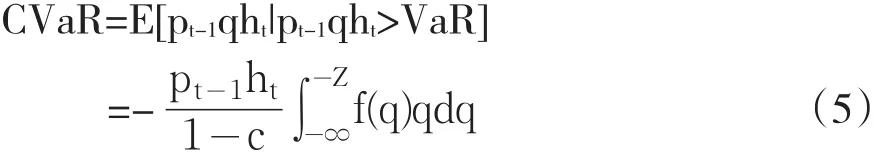
其中Pt-1表示滞后一期的资产价格,Z表示在给定置信水平α下的分位数,ht表示条件方差,f(q)表示汇率收益率序列服从分布的密度函数。分别将正态分布,T分布和GED分布的密度函数代入式(5),可得以下(6)、(7)、(8)所示的正态分布、T分布和GED分布下的CVaR的具体计算公式:
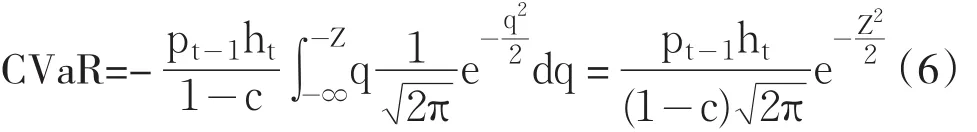
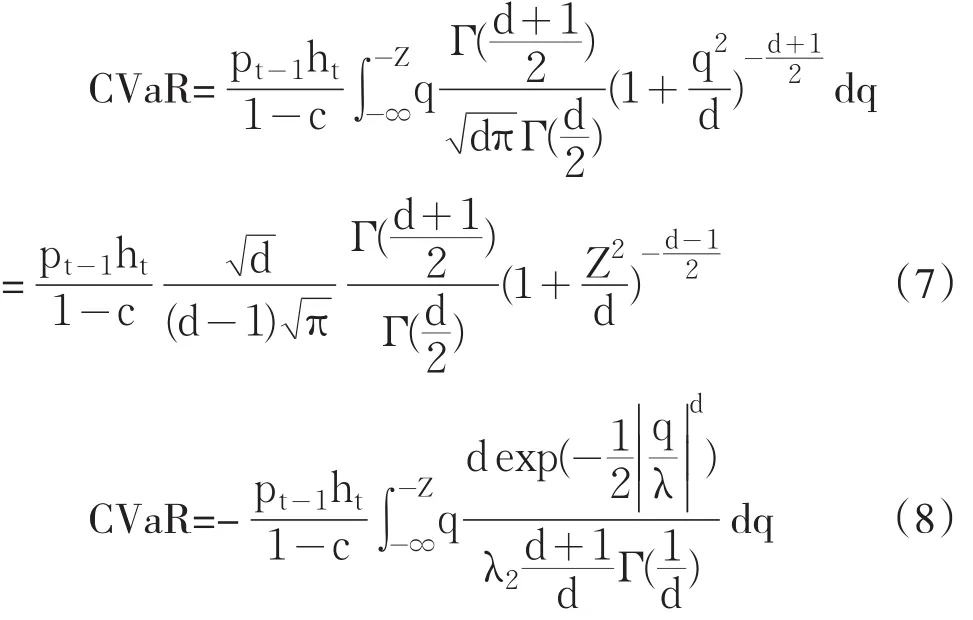
三、实证分析
(一)数据选取与处理
本文以余额宝为例,分析互联网理财产品的风险。选取余额宝对接的天弘增利宝基金的每日万份收益数据为研究对象。考虑样本数据的充足和有效性,本文选取2013年11月1日至2014年8月31日的基金每万份收益数据进行研究,数据来自聚源数据库,共有302个样本观测值。从统计角度上看,价格序列非平稳性等性质会给模型计算带来困难,相比而言,价格变动序列和回报序列具有更好的如遍历性、平稳性等统计性质,因此本文选取基金每日万份收益的对数收益率来刻画波动性,即Rt=lnPt-lnPt-1,式中Rt是基金每日万份收益的对数收益率,Pt是第t天的基金每日万份收益价格。余额宝的对数收益率的描述性统计和平稳性检验见表1,序列波动情况见下图1:

图1 余额宝的对数收益率序列

表1 余额宝的对数收益率的统计特征
由表1可知,余额宝的对数收益率JB统计量远远超过临界值,且峰度大于3,偏度为正,是右偏,所以不服从正态分布。而且由图1可以看出该序列具有明显的波动聚集性。采用ADF单位根检验方法对基金收益序列进行平稳性检验,得到ADF统计量小于1%水平下的检验标准值,所以在1%的水平下显著,说明该序列是平稳的。
对收益率序列进行异方差检验(ARCH-LM)和残差自相关检验,用拉格朗日乘数法(LM)对基金收益率序列的条件异方差进行ARCH效应统计检验,得到LM统计量均在1%的水平下显著,说明残差序列存在高阶的ARCH效应,即GARCH效应,可对收益率序列建立相应的GARCH族模型进行研究。
(二)GARCH模型的选择
本文考虑的是GARCH模型,分别在90%和95%两种置信水平下的正态分布,T分布和GED分布的情况,根据AIC信息准则进行选取,选取情况列于表2。

表2 不同分布下的GARCH模型选择
(三)VaR的计算
根据GARCH模型可求得T分布和GED分布的自由度,根据自由度可以求得分位数,再代入公式(4)计算得到VaR。VaR是一个统计估计值,其准确程度受到估计误差的影响,所以需要进行检验。我们构造一个LR统计量[9]
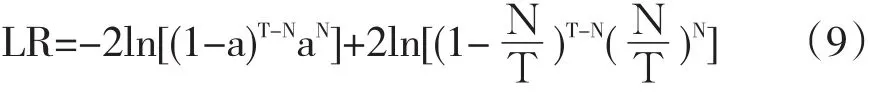
其中:T为样本长度,N为失败天数,即实际损失大于VaR值的天数,a为显著性水平。在Kupiec检验方法下,LR统计量服从自由度为1的χ2分布。非拒绝域为:

置信水平下为95%时,置信区间临界值分别为0和3.84,所以,如果在此置信度下计算出的LR统计量大于3.84,拒绝此模型;反之,则接受此模型。置信水平下为90%时,置信区间临界值分别为0.02和2.71,所以,如果在此置信水平下计算出的LR统计量大于2.71,拒绝此模型;反之,则接受此模型。
从表3可以看出,在90%和95%置信水平下,GARCH-GED模型的LR统计量是所有模型中最小的,且在模型接受域之内。GARCH-N和GARCH-T模型的LR统计量都在拒绝域内。所以GARCHGED模型对VaR的估计是合理的。

表3 VaR的计算结果
(四)CVaR的计算
根据GARCH模型可求得T分布和GED分布的自由度,根据自由度可以求得分位数,再代入公式(6)、(7)、(8)计算得到CVaR。
在对CVaR进行有效性返回检验时,我们关心的是失败时的VaR值与CVaR的差别有多大,因为CVaR在理论上是表示超过VaR的均值。于是我们定义一个检验统计量[10]:
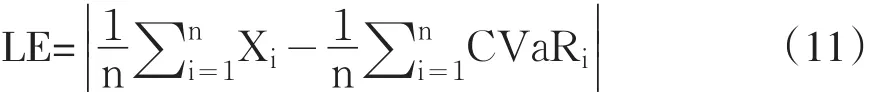

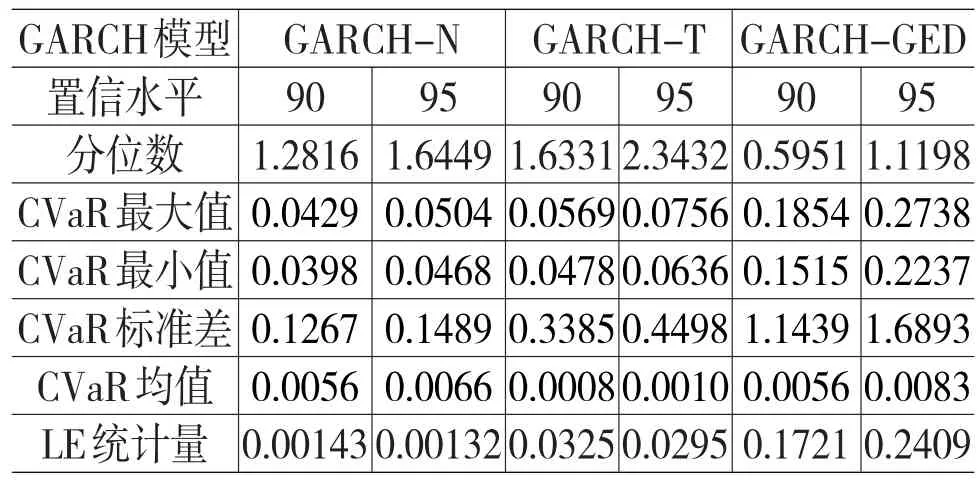
表4 CVaR的计算结果
从表4可以看出,在90%和95%置信水平下,GARCH-N模型的LE统计量是所有模型中最小的,GARCH-GED模型的LE统计量是所有模型中最大的。所以GARCH-N模型对CVaR的估计更好。
(五)确定最佳模型
从表3可以看出,在给定的置信水平下,只有GARCH-GED模型的LR统计量都在接受域之内。所以,GARCH-GED模型是最佳VaR模型。从表4可以看出,在给定的置信水平下,GARCH-N模型的LE统计量都是最小的,所以是最佳CVaR模型。得到分别在90%和95%置信水平下的最佳VaR和CVaR模型,列于表5:

表5 确定最佳模型
用最佳模型作为90%和95%置信水平下的VaR和CVaR的度量,如图2到图5所示。
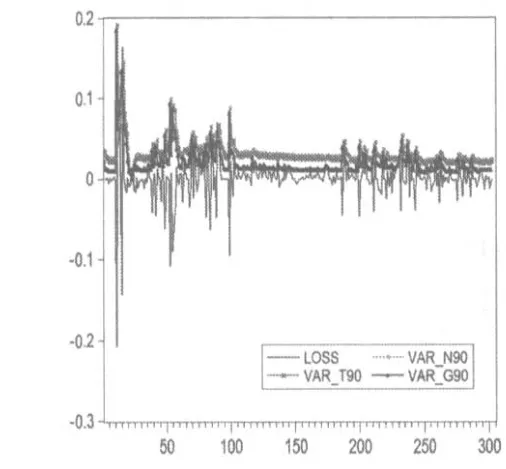
图2 90%置信水平下的VaR度量

图3 95%置信水平下的VaR度量
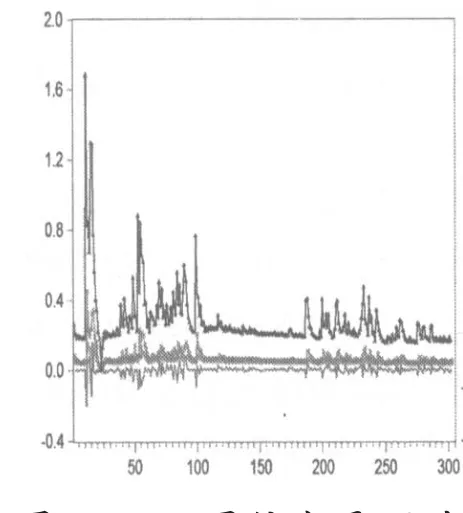
图4 90%置信水平下的CVaR度量

图5 95%置信水平下的CVaR度量
从图2到5看出,VaR和CVaR模型对对数收益的损失值有很好的度量。从图2、图3能看出GARCH-VaR-GED模型对损失值序列的度量最佳。从图4、图5能看出GARCH-CVaR-N模型对损失值序列的度量最佳。
四、结论
本文以余额宝每万份收益数据为研究样本,对我国互联网理财产品收益率的波动特点进行研究。结果表明GARCH模型可以很好地刻画收益率序列的波动性。在此基础上对互联网理财的风险进行度量,分别讨论了在90%和95%置信水平下服从正态分布,T分布和广义误差(GED)分布的GARCH-VaR和GARCH-CVaR模型。研究结果表明,对于GARCH-VaR模型在同一置信水平下,服从GED分布的模型效果最理想;对于GARCH-CVaR模型在同一置信水平下,服从N分布的模型效果最理想。对比VaR和CVaR模型,发现在相同的分布下,CVaR模型更能够包容VaR模型的失败值,能更好地覆盖可能损失的最大值,即对风险度量的效果更好。
由结果可知,目前互联网金融的风险可以用CVaR模型来很好地度量。这说明风险还处在可控范围之内,不过也不能小觑互联网金融的风险态势。由于互联网的广大受众面和极快传播速度,一旦风险失控,极易引起连锁反应,甚至冲击金融体系。CVaR模型可以作为互联网风险监控的模型之一,不仅可以度量现有的风险水平,还能发现风险失控的苗头并及时控制,对于构建风险管理体系意义重大。
[1]Artzner P,Delbaen F,Eber JH,Heah D.Coherent Measure of Risk[J].Mathematical Finance,1999, (3):203-228.
[2]Frittelli,Rosazza Gianin.Putting Order in Risk Measures[J].Journal of Banking&Finance,2002,(6): 372-379.
[3]Giorgio S.Measure ofRisk[J].Journalof Banking&Finance,2002,(26):1253-1272.
[4]Rockafeller R T.Uryasev S.Optimization of Conditional Value-at-Risk[J].The Journal of Risk, 2000,(3):21-41.
[5]Rockafeller R T.Uryasev S.Conditional Valueat-Risk for General Loss Distributions[J].Journal of Bankingand Finance,2001,(7):1443-1471.
[6]Uryasev S.Conditional value-at-risk:optimization algorithm and applications[J].Financial Engineering News,2000,(3):1-5.
[7]朱新玲,黎鹏.基于GARCH-VaR与GARCHCVaR的人民币汇率风险测度及效果对比研究[J].中南民族大学学报(自然科学版),2011,(6):129-134.
[8]Bollerslev T.Generalised autoregressive conditional heteroskedasticy[J].Journal of Econometrics, 1986,(31):307-327.
[9]JP Morgan.Riskmetrics-Technical document.3th Edition[M].New York:Morgan Guaranty Trust Company GlobalResearch,1994.
[10]黄向阳,陈学华,杨辉耀.基于条件风险价值的投资组合优化模型[J].西南交通大学学报,2004,(4):5151-5153.
(责任编辑:王淑云)
1003-4625(2014)12-0016-04
F832.39
A
2014-10-13
本文系教育部人文社科青年基金项目(13YJC790150);广东省哲学社会科学“十二五”规划项目(GD13YGL05);教育部高等学校博士学科点专项科研基金新教师类资助课题(20120172120050);中央高校基本科研业务费专项资金(2013ZB0016)。
宋光辉(1961-),男,河南信阳人,教授,博士生导师,研究方向:证券投资与分形市场;吴超(1991-),男,广东汕头人,硕士研究生,研究方向:金融工程与财务管理;吴栩(1986-),男,四川通江人,博士研究生,研究方向:证券投资与分形统计分析。

