Measurement and Correlation of Solid Drugs Solubility in Supercritical Systems

Mehdi Ardjmand, Mehrdad Mirzajanzadehand Fatemeh Zabihi*Islamic Azad University, South Tehran Branch, Graduate Faculty, Department of Chemical Engineering, Tehran, IranIslamic Azad University, Science and Research Branch, Department of Chemical Engineering, Tehran, IranIslamic Azad University, Ayatollah Amoli Branch, Department of Chemical Engineering, Amol, Iran

Measurement and Correlation of Solid Drugs Solubility in Supercritical Systems

Mehdi Ardjmand1, Mehrdad Mirzajanzadeh2and Fatemeh Zabihi3,*
1Islamic Azad University, South Tehran Branch, Graduate Faculty, Department of Chemical Engineering, Tehran, Iran2Islamic Azad University, Science and Research Branch, Department of Chemical Engineering, Tehran, Iran3Islamic Azad University, Ayatollah Amoli Branch, Department of Chemical Engineering, Amol, Iran

A dynamic experimental set-up was utilized to measure ibuprofen solubility in supercritical CO2at the pressure range of 8-13 MPa and the temperatures of 308, 313 and 318 K. Mole fraction values varied from 0.015×10−3to 3.261×10−3and correlated by using seven different semi empirical equations of state (Bartle, Modified Bartle, Mendez-Teja, Modified Mendez-Teja, Kumar-Johnson, Sung-shim and Gordillo) as well as seven cubic equations of state (van der Waals, Redlich-Kwong, Soave-Redlich-Kwong, Peng-Robinson, Stryjek-Vera, Patel-Teja-Valderana and Pazuki). Single and twin-parametric van der Walls mixing rules (vdW1, vdW2) were applied in order to estimate the supercritical solution properties. The physicochemical properties were also obtained using Joback, Lydersen and Ambrose methods. Absolute average relatives deviation (AARD) were calculated and compared for all the correlating systems. Results showed that among the cubic equations of state (EOSs) the Pazuki equation (AARD=19.85% using vdW1 and AARD=8.79% using vdW2) and SRK equation (AARD=19.20% using vdW1 and AARD=10.03% using vdW2) predicted the ibuprofen solubility in supercritical CO2with the least error in comparison to the others. Among the semi-empirical EOSs the most desirable deviation (AARD<10%) was obtained by using Modified Bartle and Modified Mendez-Teja equations in all the studied temperatures.

solubility measurement, supercritical fluids, cubic equations of state, phase equilibrium modeling, semi-empirical correlation

1 INTRODUCTION

Solubility data are the key pre-requisite of supercritical systems design and development. Since a solute solubility can be easily adjusted by changing the operational pressure and temperature, a large range of solubility database must be obtained for each solutesupercritical solvent system. Supercritical fluids technology presents a new and interesting approach for a lot of applications including extraction, purification, refinery, decontamination, particle formation, microencapsulation and many other bench, pilot plants and industrial scale processes [1-3]. rapid expansion of supercritical solutions (RESS), as an attractive and promising method, is suggested to produce fine (micro/ nano) and uniform distributed particles. Due to the solvent characteristics, this technique can be easily run in the moderate operational condition and consequently used for making fine pharmaceutics, biological and thermal degradable materials [4, 5]. A bulk solid was first dissolved in a supercritical solvent and then precipitated by depressurizing the supercritical solution to ambient pressure by passing through a heated capillary expansion device [6, 7]. Particles size distribution and morphology significantly depend upon the supercritical solution concentration. In the high solution concentration values the initial appeared nucleus aggregate immediately after precipitation due to the numerous inter-nuclear collisions. On the other hand, in the low concentrations large and widely distributed particles are initially appeared due to the low supersaturation ratio (S). Thus, acquiring a comprehensive understanding of phase behavior and equilibrium condition in supercritical binary or multi component systems is an inevitable necessity [8-10]. The solid solubility in supercritical fluid can be calculated by different thermodynamic models such as equal chemical potentials, activity coefficient, semi-empirical equations, liquid solutions and cluster solvent models. Each model is supported by some special simplifications and pre-assumptions and usually applied based on the type of processing materials and their physical properties availability [11]. In chemical potential equality model the fugacity of the solid component is taking to be equal at each phase in the equilibrium condition. An adequate equation of state (EOS) within a reliable mixing rule should be utilized for calculating the solute and supercritical solvent physical properties. Numerous equations of state are proposed in the literatures which their performance is entirely related to the operating condition range and the chemical components nature [12].

However the cubic EOSs are frequently used in fluid phase equilibrium models and the semi-empirical equations are also usefully applied owing to their easy of application and rare dependence to the material physical properties. The most common semi-empirical EOSs provide a correlation between solubility and density [13, 14]. At the current work, ibuprofen supercritical CO2solubility correlation was carried out by using equal chemical potentials model. Carbon dioxide is generally used in supercritical processes. It is an easy gas to handle, inert, nontoxic and nonflammable, and has a convenient critical condition [15]. The main goal of this paper was a general study on EOSs significancein supercritical systems solubility and equilibrium parameters estimation. Fourteen different EOSs (cubic and empirical) were utilized for solubility calculation. van der Waals (vdW), Redlich-Kwong (RK), Soave-Redlich-Kwong (SRK), Peng Robinson (PR), Stryjek-Vera (SV), Patel-Teja-Valderma (PTV) and Pazuki equations were used within single and twin-parametric van der Waals mixing rules. Then, some semi-empirical equations of states including Bartle, modified Bartle, Mendez-Santiago-Teja, modified Mendez-Teja, Gordillo, Sung-shim and Kumar-Johnson equations were applied for modeling the regression coefficients. Fitting parameters and standard deviation from experimental data were calculated using Matlab and Table curve 3D (v l.0) soft wares.

2 MATERIALS AND METHODS

2.1 Materials

Ibuprofen (Sina Daru, 99.99% purity) was used as the model component and CO2(Roham Gaz, 99.95%) was also used as the solvent. Ethanol (99.8%, Sigma Aldrich) was used in analytical grade form.

2.2 Experimental set-up and operation

A dynamic apparatus was applied to determine the ibuprofen solubility in SC-CO2. Operational system and method were explained entirely in our former work [16]. Fig. 1 illustrates that the system consists of two main parts: extraction unit and sampler loop. The liquid solvent is injected to the dissolution cells by using an HPLC pump (LC 6A, Shimadzu) in a determined pressure (±0.2%). Both cells are located in an air circulating bath after a preheater coil to control the temperature equilibrium (±0.1 °C). A 0.5 μm filter (Swage Lock) is located immediately after the equilibrium cells to prevent the solid particles to entrainment by the fluid flow. After getting to saturation point the supercritical solvent is purged to the atmosphere through a regulating valve (KPR Series, Swagelok) and a sampler coil (Stainless Steel, 3.175 mm i.d. and 1m length) in parallel, where the solute is precipitated from the solution. Saturated solubility point is determined based on the mass value of solute trapped in the sampler system and the corresponding CO2volume in each run. Experiments were accomplished in the pressure range of 8-13 MPa and three isotherms (308, 313 and 318K) conditions.

3 MODELING

3.1 Modeling based on cubic equations of state

3.1.1 Phase equilibrium modeling and solubility calculations

A supercritical fluid pressure is high enough to approximate it by compressed gas while the condensed (solid) phase is assumed in a pure state. The non-ideal behavior of the system is only limited to the supercritical phase [17]. The subscripts 1 and 2 show the supercritical phase and solid solute, respectively. The objective is calculation of the solute solubility (y2) in the fluid phase at a given temperature (T) and pressure (P). The solubility of a non-volatile pure solid solute in a supercritical fluid is given by Eq. (1) derived from equi-fugacity pre-assumption [13-15]:

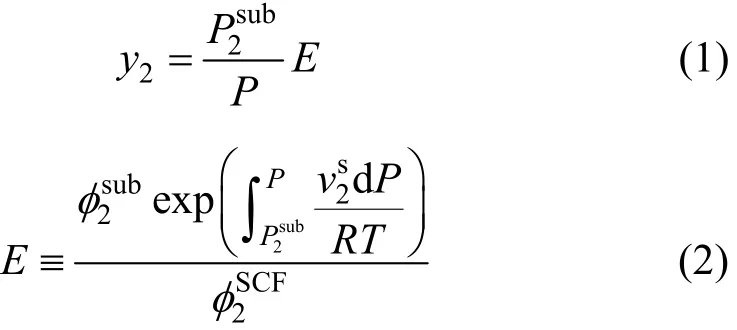
Figure 1 Schematic diagram of experimental apparatus

where the superscript s and SCF denote the solid and supercritical phase, correspondingly. The other notations include: P equilibrium pressure, T equilibriumtemperature,

3.1.2 Cubic EOSs and mixing rules All the utilized equations of state and the related mixing rules are represented in Tables 1 and 2 [19-21].

3.1.3 Component fugacity coefficient

The fugacity coefficient of a species in a solution can be calculated using Eq. (4):

Table 1 Summary of the cubic EOSs used in the present work

Table 2 Summary of the utilized mixing and combining rules

Table 3 Different sets of estimated critical and physicochemical properties of ibuprofen and physical properties of carbon dioxide

A new approach was introduced by Jiawen Hu et al. to estimate the ˆ lniφ using the lnφ. The proposed method has been used in the present study and applied in cubic equation of state and the other pressure-explicit equations [25, 26]

3.1.4 Estimation of physicochemical properties (Contribution group methods)

Three different sets of methods are used to estimate the compounds physical properties (See Table 3) [27-29]. The differences of physical property values are due to the different applied estimation methods. The accuracy and reliability of model are directly impacted by the methods used for physical properties estimation. For instance, Joback method ends to some errors in critical pressure calculation for the large molecules and organic acids [30-33]. The physicochemical properties of CO2are presented in Table 3 [34-36].

3.1.5 Objective function

In all runs of correlation AARD was considered as the objective function. According to Eq. (6) this parameter designates the mean difference between the experimental and calculated values of molar solubility (yi).

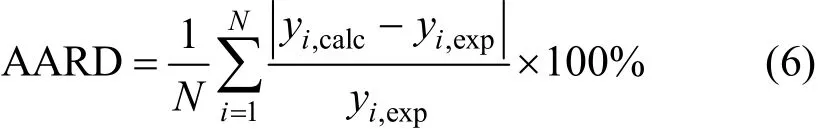
Where N, yi,expand yi,calcare the number of experimental data points, experimental and calculated values of the solubility, respectively.

3.2 Semi-empirical EOSs

Table 4 represents the equations of state used in this modeling, where2y, T,1ρ,sub2P,refP andrefρsupercritical fluid density, the sublimation pressure of the solute, the reference pressure (0.1 MPa) and reference density (700 kg·m−3), respectively. Parameters A, B and so on are the constant values obtained through the regression of experimental data (Table 4). The pressure and temperature are in Pascal and

Kelvin and y2 is the saturated mole fraction value of ibuprofen in supercritical phase. 1 ρ and ρref units in Mendez-Teja, the modified Mendez-Teja, Bartle and the modified Bartle equations are kg·m−3 and mol·L−1 for Kumar-Johnson and Sung-Shim equations. The values of sub P2 for three isotherms of Mendez-Teja equations for ibuprofen are given in Table 3. Density values for SC-CO2 are obtained from references and interpolation is applied for unreported values [37-39].

Table 4 Summary of the density-based models used in this work

4 RESULTS AND DISCUSSION

4.1 Solubility results

The solubilities obtained for ibuprofen-SC CO2system have been represented in Table 5. Molar fraction of ibuprofen in SC-CO2is indicated by y. The minimum and maximum solubility are obtained as 0.0115×10−3and 3.2610×10−3, respectively. The solubility data show a good accordance with those obtained in earlier works [40]. The latter was reported at 308, 313 and 318 K at the pressure range of 8 to 22 MPa.

Pressure increasing leads to increase the CO2density. Thus, more interactions occur between ibuprofen and CO2molecules, resulting in increasing solubility. Different trends in different isotherms are achieved. The crossover region is observed at the pressure range of 11 to 13 MPa. This may be interpreted by Eq. (3) as at a constant pressure, bothand E values affect the solubility and at the pressure less than that of crossover point. Besides, E is more effective thanin a constant pressure value. Increasing the temperature decreases the CO2-ibuprofen molecular co-covering and E value, consequently [Eq. (3)]. Above the crossover pressures value,is the most effective parameter on the solubility and E effect goes too weak, due to the considerable increase insub2P. Thus, any increase in temperature will lead to increase solubility above the crossover pressures.

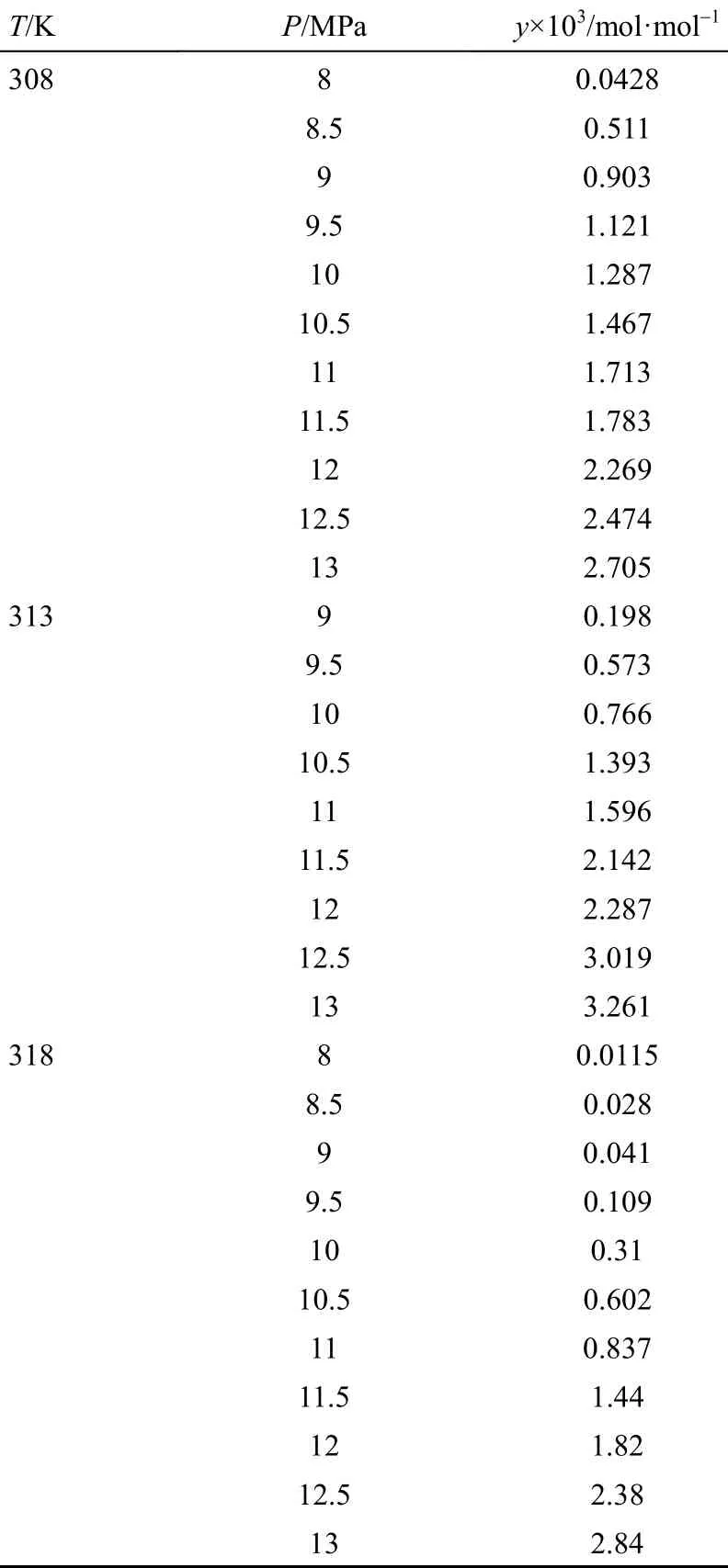
Table 5 Experimental solubility data (solid mole fraction in SC-CO2) at 308, 313 and 318 K, and 8 to 13 MPa

Normal Melting point of ibuprofen was measured by differential scanning calorimeter (DSC) system on the pressure range of 9-18.4 MPa. The solid sample was loaded into a tube cell equipped with a high resistance translucent gap. The system was placed into a water bath. CO2was gradually pumped into the cell and the melting point recorded immediately after observation of the liquid ibuprofen droplets. Table 6 shows the pressure influences on the pure ibuprofen normal melting point.

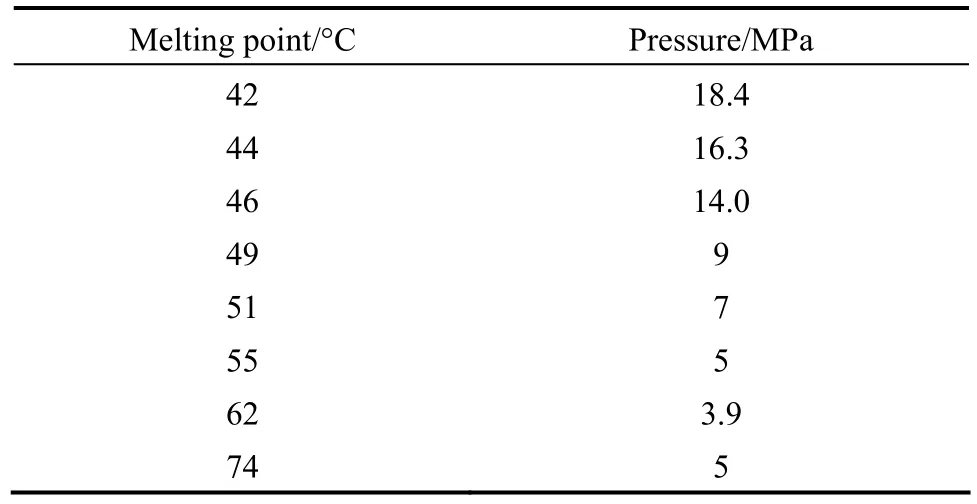
Table 6 Normal melting point variations for ibuprofen versus operating pressure

Taking into consider the melting point proves that the solute melting never occurs in our operational pressure and temperature. For the higher pressures the solute would be probably melted according to the table presented data. For pressure higher than 13 MPa, ibuprofen melting points are less than 318 K, Therefore, the pressure above 13 MPa is not valuable in operation.

4.2 Semi-empirical equations

Table 7 shows ibuprofen-SC CO2solubility correlation using seven different semi-empirical correlations in supercritical CO2extraction.

The overall AARD (averages for three isotherms) obtained using the semi-empirical equations have been presented in Fig. 2.

According to the overall AARD values, the modified Mendez-Teja and modified Bartle equations end to the most accurate correlation results (less than 10% for overall AARD) although AARD values for the Bartle equation are less than that of the modified Mendez-Teja equation for all isotherms. This advantage could be due to the specific pressure term in both equations which has not been considered in Gordillo, Kumar-Johnston and Sung-Shim equations. Moreover, sublimation pressure is removed in the M-T and modified Bartle equations term and a 1/T term is appeared instead.

Actually, considering the sublimation pressure as an adjustable parameter imposes extra errors to the calculations system. Fig. 3 shows the linear fitting in all temperatures using modified M-T. In 313 K the solubility values are predicted.

Table 7 Results of semi-empirical modeling

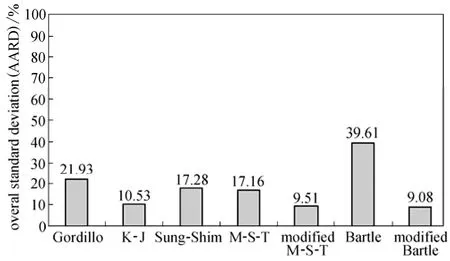
Figure 2 Overall AARD of semi-empirical models

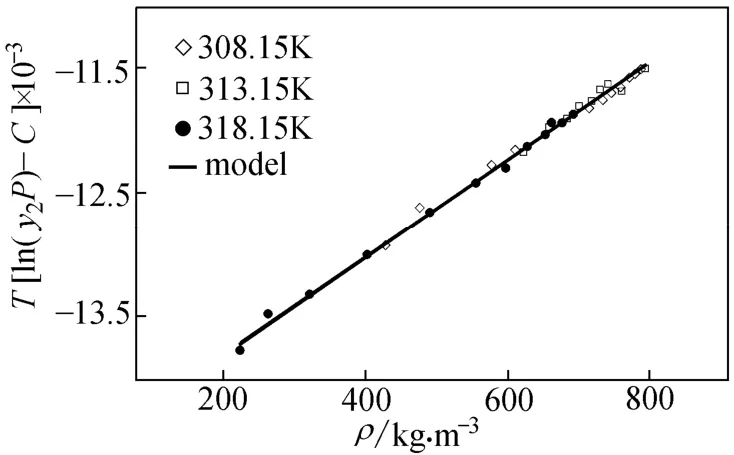
Figure 3 Comparison between the experimental data and the values calculated by modified M-S-T model

Kumar-Johnston equation representing a logarithmic form of solute mole fraction versus the SC-CO2fluid density is also more accurate than the Sung-Shim equation having the solute mole fraction logarithm term versus the supercritical fluid density logarithm.

4.3 Cubic EOSs

The solubility modeling results using seven different cubic EOSs and two different mixing rules for three isotherms at three different sets of physical properties estimation methods have been shown in Table 8.

For all the cubic EOSs in three isotherms within single parameter mixing rules, the results show that the Lydersen method is the most trustful contribution group set for physical properties estimation, except for the Pazuki EOS which results in the maximum error with Lydersen method and the minimum with Ambrose method in all the isotherms. Identical trend of results with lower AARD values are also achieved by vdW2. However, with vdW2 mixing rules, the effect of the contribution group methods type become rather inconsiderable. Actually, Table 8 shows that using vdW2 mixing rules increases the compatibility of EOSs and decreases the physical properties estimation errors in all temperatures.

Figure 4 shows the experimental solubility data correlated by PTV EOS at 313 K for three sets of physical properties using van der Waals mixing rules with one and two parameters.

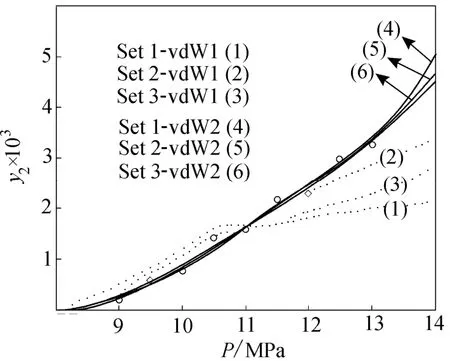
Figure 4 Solubility data correlated by PTV EOS at 313K, using three sets of physical properties and one and two parameters, van der Waals mixing rules

Contrariwise, it can be claimed that for ibuprofen-SC CO2system, data correlation by Pazuki EOS ends to authentic results at all temperatures, while the physical properties are estimated by Joback method. SRK EOS and Lydersen-Ambrose methods also show appropriate results as are applied together. By using the single parametric mixing rules at 308 and 318 K for Sets 1 and 3, Pazuki EOS for the same temperatures and Set 2, SRK EOS for 313 K, and PR EOS resulted in minimum error of correlation.

Table 8 also shows that using the single parametric mixing rules within PTV, RK and vdW EOSs at 308 and 318 K, reduces the correlation accuracy in comparison with the PR, SRK, RK and Pazuki EOSs, while by using two parametric mixing rules only vdW EQS yields a considerable deviation from experimental results of solubility data, especially for 308 and 318 K isotherms.

Inclusion of α factor in SRK equation causes error reduction comparing to RK equation. α is a function of both temperature and acentric factor. Hence, the good accuracy obtained from SRK in comparison with vdW and RK can be due to the combining role of attraction term (a) and acentric factor. Nevertheless, α factor is also observed in PR EQS. The outstanding role of b parameter (molecular volume factor) in PR indicates that this EQS is probably adequate for the large molecules. On the other hand,

the dual effect of temperature and sublimation pressure in Pazuki equation has been embedded as β factor by the term of molecular volume (b) [41-43]. The general form of SV and PR equations (except for the difference in attraction term) are quite similar, and thus AARD and corresponding parameters values are almost the same. The structure of PTV equation is basically different from the others. It includes an additional term (c parameter). Besides, the critical compressibility factor in PTV equations is never considered as a constant value. Thus, a, b and c parameters are functions of the F and the critical compressibility factors consequently.

Table 8 Correlation results for ibuprofen solubility in SC-CO, with the vdW, RK, SRK, PR, SV, PTV and Pazuki EOSs combined with the vdW1, vdW2 mixing rules by three different sets of solid component physical properties at T=308.15, 313.15 and 318.15 K

5 CONCLUSIONS

The experimental results show that increasing pressure causes increase in the ibuprofen solubility in supercritical CO2at a determined temperature, however, the existence of a crossover point at the range of 11 to 13 MPa can be based on the temperature influence on the sublimation pressure of ibuprofen.

Pressure and temperature combined effects on saturated solubility were investigated for ibuprofen-SC CO2system by using thermodynamic modeling and the calculated results were compared with the experimental data. Equal fugacity model was applied for data correlation. Fourteen equations of state were checked in the model. Two kinds of mixing rules and three different sets of group contribution methods were utilized for estimating the material physical properties. The main goal was to propose a comprehensive model including the most reliable EOS, mixing rule and group contribution set for calculating the ibuprofen solubility in SCCO2. Mean values of absolute standard deviations (AARD) were used to judge and verify the correlation accuracy.

Among semi-empirical EOSs the modified Bartle and Mendez-Teja equations with three adjustable parameters showed the minimum deviation in comparison to the other equations. In both of these equations the sublimation pressure effect was considered as a temperature dependent term. Gordillo equation has a fundamental difference with the others on which the solubility value is only a function of operating temperature and pressure and no dependency on the sublimation pressure of solid compound is observed. This claim verifies easily by perceiving the large amount of AARD resulted from correlation. Sun and Shim attempted to represent a semi-log relation between molar solubility and density in their model. Our results proved that this pattern is a weak anticipation ibuprofen-SC CO2system behavior.

The accuracy of the modeling using by cubic EOSs significantly depends on the method used to estimate the physiochemical and critical properties of both fluid and solid species. Results showed that by vdW2 approaches for all the isotherms, Lydersen method results have had trustable agreement with the empirical data in contrast to the Ambrose method. Conversely, the results of Ambrose caused less error in comparison with the Joback method. The latter method was unreliable when the single parametric rules were used. In general, two parametric mixing rules worked well for all the cubic EOSs. Pazuki and SRK equations were the most reliable EOSs for approving our experimental data. PR and SV equations almost made good correlation and the most deviations were resulted by the vdW and RK equations. PTV equation applied within the vdW2 and vdW1 ended to middle amounts of overall AARD (13% and 34%) correspondingly.

NOMENCLATURE

REFERENCES

1 Chitanvis, M.S., Physics of RESS Solutions: A First Approach, Theoritical Divisions, MSB268, Los Alamos National Laboratory, New Mexico (2007).

2 Yildiz, N., Tuna, S., Duker, O., Calimi, A., “Micronization of salicylic acid and taxol (paclitaxel) by rapid expansion of supercritical fluids (RESS)”, J. Supercrit. Fluid, 41, 440-451 (2007).

3 Defne, K., Akman, U., Hortacsu, O., “Micronization of ibuprofen by RESS”, J. Supercrit. Fluids, 26, 17-31 (2006).

4 Atila, C., Yıldız, N., Alımlı, A.C., “Particle size design of digitoxin in supercritical fluids”, J. Supercrit. Fluids, 51, 404-411 (2010).

5 Türk, M., Lietzow, R., “Formation and stabilization of submicron particles via rapid expansion processes”, J. Supercrit. Fluids, 45, 346-355 (2008).

6 Hirunsit, P., Huang, Z., Srinophakon, T., Charoenchaitrakool, M., Kawi, S., “Particle formation of ibuprofen-supercritical CO2system from rapid expansion of supercritical solution”, J. Powder Tech., 154, 83-94 (2005).

7 Fages, J., Luchard, H., Letorneau, J., Sauceau, M., “A three step supercritical process to improve the dissolution rate of eflucimibe”, J. Powder Tech., 141, 219-226 (2004).

8 Zabihi, F., Akbarnejad, M.M., Vaziri, A., Arjomand, M., Seyfkordi, A.A., “Drug nano-particles formation by supercritical rapid expansion method—operational condition effects investigation”, IJCCE, 30, 441-449 (2009).

9 Zabihi, F., Vaziri, A., Akbarnejad, M.M., Arjomand, M., Otady, M., Bozorgmanesh, A.R., “A novel mathematical method for prediction of rapid expansion of supercritical solution (RESS) processed ibuprofen powder size distribution”, Korean J. Chem. Eng., 27, 1601-1607 (2010).

10 Bae, H., Jeon, J., Lee, H., “Influence of Co-solvent on dye solubility in supercritical carbon dioxide”, Fluid Phase Equilibria, 222-223, 119-125 (2004).

11 Kong-Wei, C., Muoi, T., Yan-Ping, C., “Calculations of solid solubility in supercritical fluids using a simplified cluster solvation model”, Fluid Phase Equilib., 214, 169-186 (2003).

12 Matias, A.A., Nunes, A.V.M., Casimiro, T., Duarte, M.M.C., “Solubility of coenzyme Q10in supercritical carbon dioxide”, J. Supercrit. Fluids, 28, 201-206 (2004).

13 Coimbra, P., Duarte, C.M.M., de Susa, H.C., “Cubic equation-of-state correlation of the solubility of some anti-inflammatory drugs in supercritical carbon dioxide”, J. Fluid Phase Equilib., 239, 188-199 (2006).

14 Sparks, D.L., Hernandez, R., Estevez, L.A., “Evaluation of density-based models for the solubility of solids in supercritical carbon dioxide and formulation of a new model”, J. Chem. Eng. Sci., 63, 4292-4301 (2008).

15 Prausntz, J.M., Lichtenthaler, R.N., Molecular Thermodynamics of Fluid Phase Equilibria., 3rd ed., Prentice Hall PTR, New Jersey (1986).

16 Mirzajanzadeh, M., Zabihi, F., Ardjmand, M., “Measurement and correlation of ibuprofen in supercritical carbon dioxide using Stryjek and Vera EOS”, IJChE, 7, 42-49 (2010).

17 Madras, G., “Thermodynamic modeling of the solubilities of fatty acids in supercritical fluids”, Fluid Phase Equilibria, 220, 167-169 (2004).

18 Nobre, P.B., Luisa, G., Matos, P.G.S., Cristino, A.F., Palavra, A.F., Mendes, R.L., “Supercritical extraction of lycopene from tomato industrial wastes with ethane”, J. Molecules, 17, 8397-8407 (2012).

19 Reddy, S.N., Giridhar, M., “A new semi-empirical model for correlating the solubilities of solids in supercritical carbon dioxide with cosolvents”, J. Fluid Phase Equilib., 310, 207-212 (2011).

20 Yermakova, A., Anikeev, V.I., “Thermodynamic calculations in the modeling of multiphase processes and reactors”, Ind. Eng. Chem. Res., 39, 1453-1472 (2000).

21 Dashtizadeh, A., Pazuki, G.R., Taghikhani, V., Ghotbi, C., “A new two-parameter cubic equation of state for predicting phase behavior of pure compounds and mixtures”, J. Fluid Phase Equilib., 242, 19-28 (2004).

22 Ashoura, I., Almehaideba, R., Fateenb, S.E., Aly, G., “Representation of solid-supercritical fluid phase equilibria using cubic equations of state”, J. Fluid Phase Equilib., 167 (1), 41-61 (2000).

23 Duan, Z., Hu, J., “A new cubic equation of state and its applications to the modeling of vapor-liquid equilibria and volumetric properties”, Geochim. Cosmochim. Acta, 68, 2997-3003 (2004).

24 Abildskova, J., Martin, C., Ellegaarda, D., O’Connel, J.P., “Correlation of phase equilibria and liquid densities for gases with ionic liquids”, J. Fluid Phase Equilib., 286 (1), 95-106 (2009).

25 Lyman, W.J., Reehl, W.F., Rosenblatt, D.H., Hand Book of Chemical Property Estimation Methods, McGraw-Hill, NY (1982).

26 Zekovic, Z., Lepojevic, Z., Tolic, A., “Modeling of the thyme-supercritical carbon dioxide extraction system: the influence of extraction time and carbon dioxide pressure”, J. Sep. Sci. Tech., 38, 1161-1184 (2003).

27 Reid, R.C., Prausnitz, J.M., Poling, B.E., The Properties of Gases and Liquids, 4th ed., McGraw-Hill, NY (1987).

28 Poling, B.E., Prausnitz, J.M., O’Connell, J.P., The Properties of Gases and Liquids, 5th ed., McGraw-Hill, NY (2001).

29 Karim, A.M., Kassim, D.M., Hameed, M.S., “Phase equilibrium study for the separation of solid components using supercritical carbon dioxide”, The Open Thermodynamics J., 4, 201-212 (2010).

30 Li, Q.S., Zhang, Z., Zhong, C., Liu, Y., Zhou, Q., “Modeling of the solubility of solid solutes in supercritical CO2with and without cosolvent using solution theory”, J. Fluid Phase Equilibria, 207, 183-192 (2003).

31 Huang, S.Y., Tang, M., Ho, S.L., Chen, Y.P., “Solubilities of N-phenylacetamide, 2-methyl-N-phenylacetamide and 4-methyl-N-phenylacetamide in Supercritical carbon dioxide”, J. Supercrit. Fluids, 42, 165-316 (2007).

32 Teja, A.S., Eckert, C.A., “Commentary on supercritical fluids: research and application”, Ind. Eng. Chem. Res. 39, 4442-4452 (2000).

33 Mehdizadeh, B., Movagharnejad, K., “A comparison between neural network method and semi empirical equations to predict the solubility of different compounds in supercritical carbon dioxid”, J. Fluid Phase Equilib., 41, 187-194 (2007).

34 Jafari Nejad, S., Khansary, M.A., Amiri, F., “Modeling of solubility of disperse blue dyes in supercritical carbon dioxide using equation of states (EOSs)”, Int. J. Chem. Eng. App., 2 (4), 272-277 (2011).

35 Catchpole, O.J., Tallon, S.J., Dyer, P.J., Lan, J.S., Jensen, B.,“Measurement and modeling of urea solubility in supercritical CO2and CO2+ ethanol mixtures”, J. Fluid Phase Equilib., 237, 12-218 (2011).

36 Huang, Z., Lu, W.D., Kawi, S., Chiew, Y.C., “Solubility of aspirin in supercritical carbon dioxide with and without acetone”, J. Chem. Eng. Data, 49, 1323-1327 (2004).

37 Charoenchaitrakool, M., Dehghani, F., Foster, N.R., “Micronization by rapid expansion of supercritical solution to enhance the dissolution rate of poorly water-soluble pharmaceuticals”, Ind. Eng. Chem. Res., 39, 4794-4802 (2000).

38 Su, C.S., Chen, Y.P., “Correlation for the solubilities of pharmaceutical compounds in supercritical carbon dioxide”, J. Fluid Phase Equilib., 254, 167-173 (2007).

39 Cheng, K.W., Tang, M., Chen, Y.P., “Calculations of solid solubility in supercritical fluids using a simplified cluster solvation model”, J. Fluid Phase Equilib., 214, 169-181 (2003).

40 Issaoui, A., Moussa, A.B., Ksibi, H., “Correlation of the binary interaction factor for polar solutes dissolved in supercritical carbon dioxide”, Int. J. Thermodynamics, 14 (1), 37-42 (2011).

41 Kraska, T., Leonhard, K.O., Tuma, D., Schneider, G.M., “Correlation of the solubility of low-volatile organic compounds in near- and supercritical fluids. Part I: Applications to adamantane and β-carotene”, J. Supercrit. Fluids, 23 (3), 209-224 (2002).

42 Hosaindokht, M.R., Bozorgmehr, M.R., “Calculation of solubility of methimazole, phenazopyridine and propranolol in supercritical carbon dioxide”, J. Supercritical Fluids, 43, 390-397 (2008).

43 Schultz, A.J., Shaul, K.P.S., Shu, Y., Kofke, D.A., “Modeling solubility in supercritical fluids via the virial equation of state”, J. Supercritical Fluids, 55, 479-484 (2010).

2012-11-14, accepted 2013-05-16.

* To whom correspondence should be addressed. E-mail: elyze_125@hotmail.com