Determination and Correlation of Solubility for D-Xylose in Volatile Fatty Acid Solvents*
Determination and Correlation of Solubility for D-Xylose in Volatile Fatty Acid Solvents*
LI Tao (李涛), CHEN Feixiong (陈飞雄), JIANG Zhenxi (江振西) and REN Baozeng (任保增)**
School of Chemical Engineering and Energy, Zhengzhou University, Zhengzhou 450001, China
The solubility of D-xylose in formic acid and binary solvents of formic acid with formic acid and acetic acid, propionic acid, n-butyric acid or isobutyric acid was measured in the temperature range from 300.35 to 325.05 K using the synthetic method by a laser monitoring technique at atmospheric pressure. The solid-liquid equilibrium data will provide essential support for industrial design and further theoretical study. The experimental data show that the solubility of D-xylose in formic acid and in the mixtures of formic acid + acetic acid (1︰1), formic acid + propionic acid (1︰1), formic acid + n-butyric acid (1︰1), and formic acid + isobutyric acid (1︰1) increases with temperature. The Apelblat equation, the λh model, and the ideal solution equation correlate the solubility data well.
solid-liquid equilibrium, solubility, D-xylose
1 INTRODUCTION
Shift of the dependence from fossil-based resources to biomass-based resources is important for a sustainable industrial society and reduction of greenhouse gas emissions [1]. In recent years, biomass processing for the production of value-added chemicals has come to the forefront of research on biological and chemical engineering [2, 3]. D-xylose is a pentoses present abundantly in lignocellulosic biomass, which can be converted into useful producs such as D-xylonic acid, ethanol, xylitol, bacterial cellulose, and D-xylonate [4-7]. The yield and quality of D-xylose depend on the purity of raw materials. For purification of D-xylose, solubility data are required. The solubility data for D-xylose in formic acid and formic acid with other volatile fatty acids have not been reported. In this study, we measure the solubility of D-xylose in formic acid and binary solvent systems with formic acid and acetic acid, propionic acid, n-butyric acid or isobutyric acid from 300.35 to 325.05 K by a laster monitoring technique. The experimental data are correlated with the Apelblat equation, the λh model, and the ideal solution equation.
2 EXPERIMENTAL
2.1 Materials
A white crystalline powder of D-xylose (C5H10O5, molecular mass 150.14) used in the experiments was obtained from Shanghai Hualan Chemical Technology Co., Ltd., China, with mass fraction purity higher than 99.0%, determined by HPLC (type Agilent 1200, Agilent Technologies). It was dried in vacuum at 313.15 K for 24 h and stored in a desiccator. Formic acid (mass fraction purity ≥98%) was purchased from Tianjin Guangfu Fine Chemical Research Institute. Acetic acid (mass fraction purity ≥99.5%) was purchased from Yantai Shuangshuang Chemical Co., Ltd. Propionic acid (mass fraction purity ≥99%) was purchased from Tianjin Kermel Chemical Reagent Development Center. N-Butyric acid (mass fraction purity≥99%) was purchased from Tianjin Bodi Chemical Holding Co., Ltd. Isobutyric acid (mass fraction purity≥99.5%) was purchased from Tianjin Kermel Chemical Reagent Co., Ltd. All the solvents used in the experiments are of AR grade and checked by gas chromatography.
2.2 Experimental procedure
The solubility of a solid in a solvent was determined by synthetic method [8-10]. The apparatus and method were described in our previous work [9]. To verify the uncertainty of the measurement, the solubility data for benzoic acid in water were compared with the values in literature [11]. The average relative error was less than 0.03, so this experimental technique was reliable.
3 RESULTS AND DISCUSSION
The relationship between solubility and temperature is generally expressed as the Apelblat equation, which can be deduced from Clausius-Clapeyron equation [12-15]

where A, B and C are empirical constants, χ is the solubility in mole fraction at system temperature T (K).
The λh model developed by Buchowski et al. [8, 16] is a semi-empirical equation,

where λ and h are the model parameters determined by experimental data, χ is the solubility in mole fraction, and Tmis the normal melting temperature.
A universal equation for solid-liquid equilibrium [17, 18] based on thermodynamic principles is

where ΔHi, Ttp,i, ΔCp,i, Ptp,i, and λiare, respectively, molar enthalpy of fusion, triple-point temperature, difference of heat capacities between sub-cooled liquid and solid, triple point pressure, and activity coefficient for component i, χiis the solubility (mole fraction) of component i at system temperature T and pressure p, and R is the universal gas constant.
Equation (3) is frequently simplified by replacing the triple-point temperature (Ttp,i) with the normal melting temperature (Tm,i). It can be further simplified by neglecting the last two terms on the right-hand side [19]. The contribution of heat-capacity difference is often minor and there is no solid-to-solid conversion from T to Ttp. Eq. (3) becomes
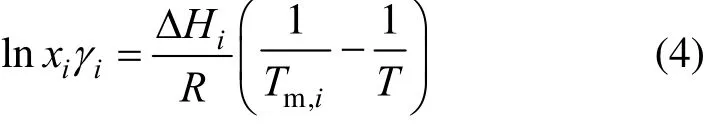
For ideal solutions (γi=1), simplified form [20, 21]

where A and B are the model parameters.
The solubility data of D-xylose in different solvents are listed in Table 1. The parameters in Eqs. (1), (2), and (5) are listed in Table 2, where χ(alp), χ(λh)and χ(ideal) are the calculation values of the Apelblat equation, the λh model and the ideal solution equation, respectively. The experimental points and calculated values are shown in Figs. 1-3. The ADD is the relative error defined as

Table 1 Mole fraction solubility χ of D-xylose in different solvents
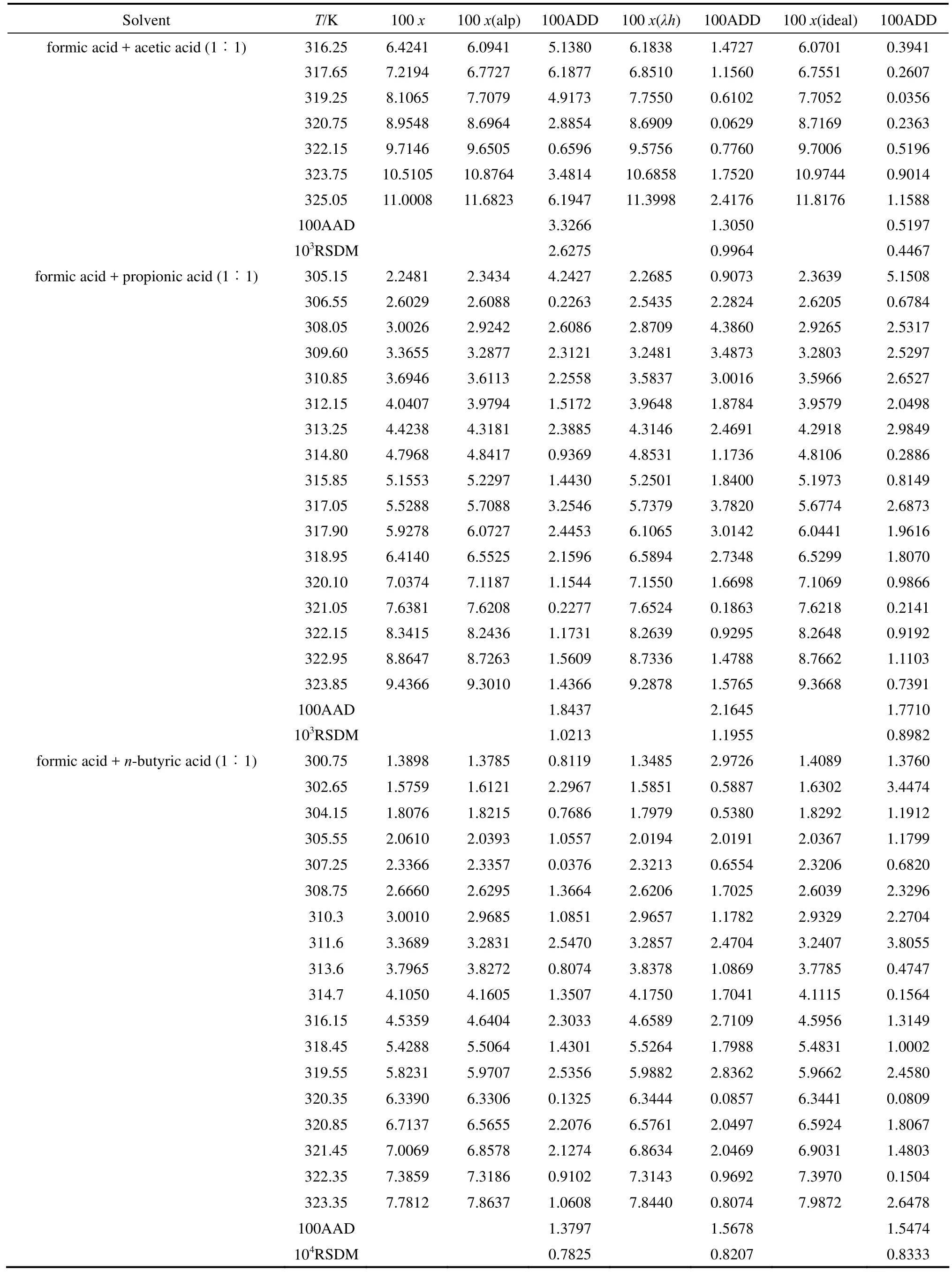
Table 1 (Continued)

Table 1 (Continued)

Table 2 Parameters of Eqs. (1), (2) and (5) for D-xylose in different solvents
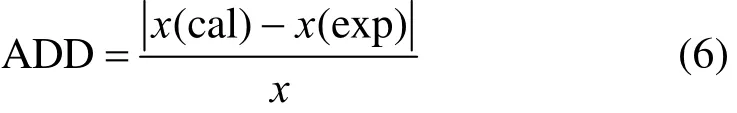
The average absolute deviation (AAD) is

The root-mean square deviation (RMSD) is defined as
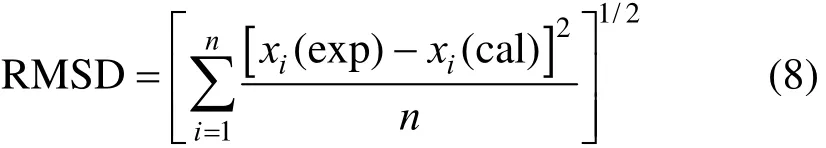
where n is the number of experimental points, χ(exp) and χ(cal) are the experimental and calculated solubility, respectively.
Tables 1 and 2 and Figs. 1 to 3 showed that (i) the solubility curves are similar and the solubility increases with temperature rapidly; (ii) the Apelblat equation is more accurate than the other two models for systems of formic acid, formic acid + n-butyric acid, and formic acid + isobutyric acid, while the ideal solution model is better for systems of formic acid + acetic acid and formic acid + propionic acid; (iii) the solubility of D-xylose follows the order: formic acid> formic acid + acetic acid (1︰1)>formic acid + propionic acid (1︰1)>formic acid + n-butyric acid (1︰1) and formic acid + isobutyric acid (1︰1) ; (iv) the solubility of D-xylose in the four binary solvents is far lower than that in formic acid, indicating that the solubility increases with the polarity of solvents. Since the solubility of D-xylose is low at low temperatures, the recrystallization of D-xylose is possible.
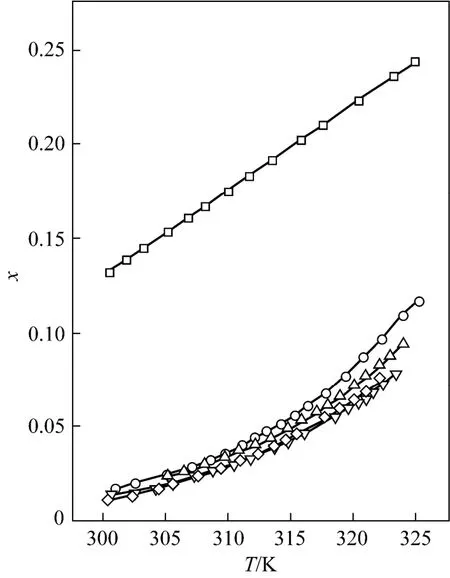
Figure 1 Mole fraction solubility χ against temperature for D-xylose in different solvents fitted with the Apelbalt equation□ formic acid; ○ formic acid + acetic acid (1︰1); △ formic acid + propionic acid (1︰1); ▽ formic acid + n-butyric acid (1︰1); ◇ formic acid + isobutyric acid (1︰1)
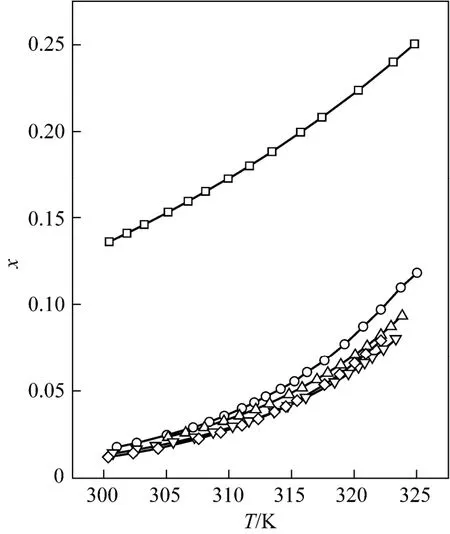
Figure 3 Mole fraction solubility χ against temperature for D-xylose in different solvents fitted with the ideal model□ formic acid; ○ formic acid + acetic acid (1︰1); △ formic acid + propionic acid (1︰1); ▽ formic acid + n-butyric acid (1︰1); ◇ formic acid + isobutyric acid (1︰1)
4 CONCLUSIONS

Figure 2 Mole fraction solubility χ against temperature for D-xylose in different solvents fitted with the λh model□ formic acid; ○ formic acid + acetic acid (1︰1); △ formic acid + propionic acid (1︰1); ▽ formic acid + n-butyric acid (1︰1); ◇ formic acid + isobutyric acid (1︰1)
New experimental results for the solubility of D-xylose in formic acid and binary mixed solvents with formic acid and acetic acid, propionic acid, n-butyric acid or isobutyric acid are presented. The solubility increases with temperature in the temperature range from 300.35 to 325.05 K and is in following order: formic acid>formic acid + acetic acid (1︰1)> formic acid + propionic acid (1︰1)>formic acid + n-butyric acid (1︰1) and formic acid + isobutyric acid (1︰1). The Apelblat equation is more accurate for systems of formic acid, formic acid + n-butyric acid (1︰1), and formic acid + isobutyric acid (1︰1), while the ideal solution model is better for systems of formic acid + acetic acid (1︰1) and formic acid + propionic acid (1︰1). These correlations can be used to calculate solubility data of D-xylose in industrial application. These volatile fatty acid solvents are beneficial for the recrystallization of D-xylose.
REFERENCES
1 Ragauska, A.J., Williams, C.K., Davison, B.H., Britovsek, G.., Cairney, J., Eckert, C.A., Frederick Jr., W.J., Hallett, J.P., Leak, D.J., Liott, C.L., Mielen, J.R., Murphy, R., Templer, R., Tschaplinski, T., “The path forward for biofuels and biomaterials”, Science, 311 (5760), 484-489 (2006).
2 FitzPatrick, M., Champagne, P., Cunningham, M.F., Whitney, R.A.,“A biorefinery processing perspective: Treatment of lignocellulosic materials for the production of value-added products”, Bioresour. Technol., 101 (23), 8915-8922 (2010).
3 Gao, P.F., Fan, D.D., Luo, Y.E., Ma, X.X., Ma, P., Hui, J.F., Zhu, C.H., “Efficient and comprehensive utilization of hemicellulose in the corn stover”, Chin. J. Chem. Eng., 17 (2), 350-354 (2009)
4 Nygard, Y., Toivari, M.H., Penttiä, M., Ruohonen, L., Wiebe, M.G.,“Bioconversion of D-xylose to D-xylonate with Kluyveromyces lactis”, Metabolic Engineering, 13 (4), 383-391 (2011).
5 Sánchez, S., Bravob, V., Moya., A.J., Castro, E., Camacho, F., “Influence of temperature on the fermentation of D-xylose by Pachysolen tannophilus to produce ethanol and xylitol”, Process Biochemistry, 39 (6), 673-679 (2004).
6 Ishihara, M., Matsunaga, M., Hayashi, N., Tišler, V., “Utilization of D-xylose as carbon source for production of bacterial cellulose”, Enzyme and Microbial Technology, 31 (7), 986-991 (2002).
7 Toivari, M.H., Ruohonen, L., Richard, P., Penttilä, M., Wiebe, M.G.,“Saccharomyces cerevisiae engineered to produce D-xylonate”, Appl. Microb. Biotechnol., 88 (3), 751-760 (2010).
8 Buchowski, H., Ksiazczak, A., Pietrzyk, S., “Solvent activity along a saturation line and solubility of hydrogen-bonding solids”, J. Phys. Chem., 84 (9), 975-979 (1980).
9 Chen, F.X., Zhao, M.R., Ren, B.Z., Zhou, C.R., Peng, F.F., “Solubility of diosgenin in different solvents”, J. Chem. Thermodyn., 47, 341-346 (2012).
10 Shi, X.H., Zhou, C.R., Gao, Y.G., Chen, X.Z., “Measurement and correlation for solubility of (S)-(+)-2,2-dimethylcyclopropane carbox amide in different solvents”, Chin. J. Chem. Eng., 14 (4), 547-550 (2006).
11 Liu, G.Q., Ma, L.X., Liu, J., Manual of Chemical and Physical Properties (Organic Volume), Chemical Industry Press, Beijing (2002).
12 Apelblat, A., Manzurola, E., “Solubilities of L-aspartic, DL-aspartic, DL-glutamic, p-hydroxybenzoic, o-anistic, p-anisic, and itaconic acids in water from T=278 K to T=345 K”, J. Chem. Thermodyn., 29, 1527-1533 (1997).
13 Apelblat, A., Manzurola, E., “Solubilities of oacetylsalicylic, 4-aminosalicylic, 3,5-dinitrosalicylic, and ptoluic acid, and magnesium DL aspartate in water from T=(278 to 348) K”, J. Chem. Thermodyn., 31, 85-91 (1999).
14 Manzurola, E., Apelblat, A., “Solubilities of L-glutamic acid, 3-nitrobenzoic acid, p-toluic acid, calcium-L-lactate, calcium gluconate, magnesium-DL-aspartate, and magnesium-L-lactate in water”, J. Chem. Thermodyn, 34, l127-l136 (2002).
15 Chen, F.X., Zhao, M.R., Liu, C.C., Peng, F.F., Ren, B.Z., “Determination and correlation of the solubility for diosgenin in alcohol solvents”, J. Chem. Thermodynamics, 50, 1-6 (2012).
16 Buchowski, H., “Solubility of solids in liquids: one-parameter solubility equation”, J. Fluid Phase Equilib., 25 (3), 273-278 (1986).
17 Stanley, M.W., Phase Equilibria in Chemical Engineering, Butterworth, New York, (1985).
18 Ksiazczak, A., Moorthi, K., Nagata, I., “Solid-solid transition and solubility of even n-alkanes”, Fluid Phase Equilib., 95, 15-29 (1994).
19 Prausnitz, J.M., Lichtenthaler, R.N., Molecular Thermodynamics of Fluid-Phase Equilibria, 2nd ed., Prentice-Hall, Englewood Cliffs, NJ (1986).
20 Li, Y., Wang, F.A., Ren, B.Z., “Measurement and correlation of solubilities of cefpirome sulfate in aqueous alcohol solution between (278.15 and 308.15) K”, J. Chem. Eng. Data, 55, 5375-5381 (2010).
21 Yang, J., Zhou, C.R., Shi, X.H., “Determination and correlation of the solubility for taurine in water and organic solvent systems”, J. Chem. Eng. Data, 55, 2620-2623 (2010).
2012-07-20, accepted 2013-01-30.
* Supported by Science and Technology Breakthrough Major Project in Henan Province (112101210200).
** To whom correspondence should be addressed. E-mail: renbz@zzu.edu.cn
 Chinese Journal of Chemical Engineering2014年4期
Chinese Journal of Chemical Engineering2014年4期
- Chinese Journal of Chemical Engineering的其它文章
- An Approach to Formulation of FNLP with Complex Piecewise Linear Membership Functions
- Effects of Assistant Solvents and Mixing Intensity on the Bromination Process of Butyl Rubber*
- Impacts of Power Density on Heavy Metal Release During Ultrasonic Sludge Treatment Process*
- One Step Preparation of Sulfonated Solid Catalyst and Its Effect in Esterification Reaction*
- Support Effects on Thiophene Hydrodesulfurization over Co-Mo-Ni/Al2O3and Co-Mo-Ni/TiO2-Al2O3Catalysts*
- Determination and Correlation of Solubilities of Four Novel Benzothiazolium Ionic Liquids with6PF−in Six Alcohols*
