基于四传感器方阵的地震动目标方位角估计*
谢 逍, 董大伟, 华春蓉, 闫 兵
(西南交通大学 机械工程学院,四川 成都 610031)
基于四传感器方阵的地震动目标方位角估计*
谢 逍, 董大伟, 华春蓉, 闫 兵
(西南交通大学 机械工程学院,四川 成都 610031)
针对地震动目标定位中的信号传播速度不确定性问题,提出了基于到达时间差的四传感器方阵目标方位角估计方法。从理论上推导出四传感器方阵下的目标方位角估计带边界及其最大带宽值,证明了信号传播速度与目标方位角估计之间的弱相关性。根据仿真计算深入探讨了信号传播速度和时延测量误差对目标方位角估计精度的影响。外场实验结果证明:这一方法的地震动目标方位角平均估计误差小于采用三轴地震动传感器的方法,具有一定的实用价值。
目标方位角估计; 地震动信号; 传播速度; 四传感器方阵
0 引 言
无人值守地面传感器 (unattended ground sensor,UGS) 系统作为地面目标侦察的一项关键技术在近些年来得到了迅速发展,并被广泛运用于军事和商用各领域。地震动传感器是其重要组成部分,具有抗电磁能力强、能耗和成本相对较低等优势,因此,重点参与了地面目标检测和识别分类的功能实现,然而通过地震动传感器进行精确的目标实时定位一直是研究难题。
在众多的目标定位方法中,基于到达时间差(time difference of arrival,TDOA)或时延的测向定位技术[1,2]因其抗干扰能力强,定位精度较高和设备要求简单等特点而成为了目前的研究热点。其基本原理是利用多个传感器测量信号时延,并联合信号传播速度对目标方位角进行估计,最后通过传感器阵列交叉定位[3]。目前针对测向定位中侧边区定位误差较大和现实信号环境中存在干扰信号和噪声等问题,文献[4~6]分别提出了改进的时延测向算法;文献[7]则推导了四传感器阵列的定向算法和最佳阵列布局。然而这些研究对于地震动信号传播速度的不确定性问题却没有涉及。另一方面,文献[8~10]分别通过建立带有主动参数校正的地震动信号传播模型和寻找在超定系统中最小二乘解的方法估计信号传播速度,但计算开销较大且估计结果不够精确。文献[11~13]尝试采用三轴地震动传感器在信号传播速度未知的情况下进行目标方位角估计,而实验结果显示其平均角度估计误差达到了20°。
本文提出了一种基于四传感器方阵的时延测向定位方法,能够在信号传播速度不定情况下准确估计目标方位角,对复杂未知地质状况下的地震动目标定位有一定指导意义和应用价值。
1 基于四传感器方阵的目标方位角估计
首先推导四传感器方阵下的定位方程。如图1所示,设一大小为l=2d的四传感器方阵位于坐标原点,目标源坐标(x,y),其关于阵列的方位角为θ,到阵列中心距离为r。
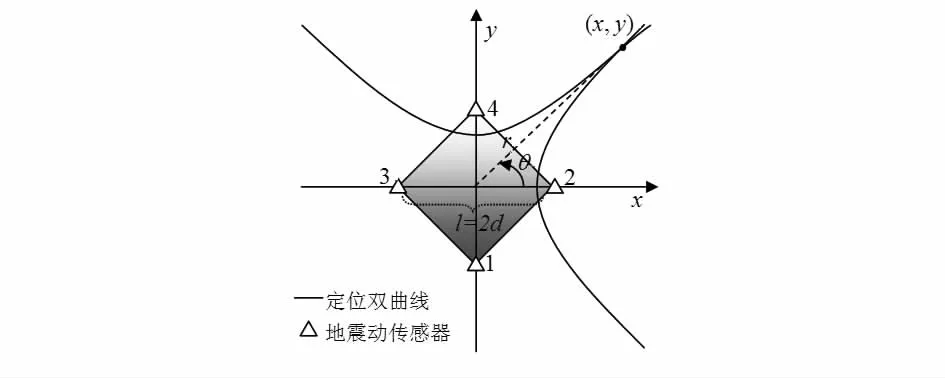
图1 四传感器方阵双曲线定位Fig 1 Hyperbolic localization using four-sensor square array
不失一般性,令目标源坐标位于第一象限,k为坐标斜率,其方位角θ可表示为
y=kx,k=tanθ≥0.
(1)
由传感器阵列的正交性,可知其标准定位双曲线方程为
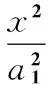
(2)
其中
式中τ1,4和τ3,2分别为两相应传感器间的时延,v为信号传播速度。容易解得目标源坐标
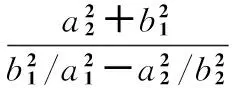
(3)
代入式(1)得到目标方位角估计
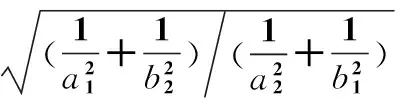
(4)
容易看出,目标源坐标及其方位角的估计值与时延,信号传播速度和阵列大小均有关系。在地震动目标定位中,时延可由广义互相关算法[14]计算得到,阵列大小为常数,而信号传播速度往往是无法精确测量的,因此,以式(3)直接确定目标源位置会产生较大偏差。但是通过理论分析能够证明,信号传播速度对式(4)中方位角估计值的影响十分有限。
2 目标方位角估计带及其带宽
现讨论两种目标定位情况:首先假设目标源位于距传感器阵列较远处,其地震动信号到达阵列时可近似为平行直线,如图2所示,r3,2和r1,4分别为目标源到相应传感器间的距离之差。由此时的几何关系容易推导出目标方位角估计中的远边界θfar,且这一边界只与时延有关而不受传播速度的影响。当目标靠近传感器阵列时,其地震动信号不能再被视为一系列的平行直线,此时通过联解方程(1)和(2)可以推导出目标方位角估计中的近边界θnear。省略具体推导过程,结合两个边界可得到目标方位角估计带的表达式
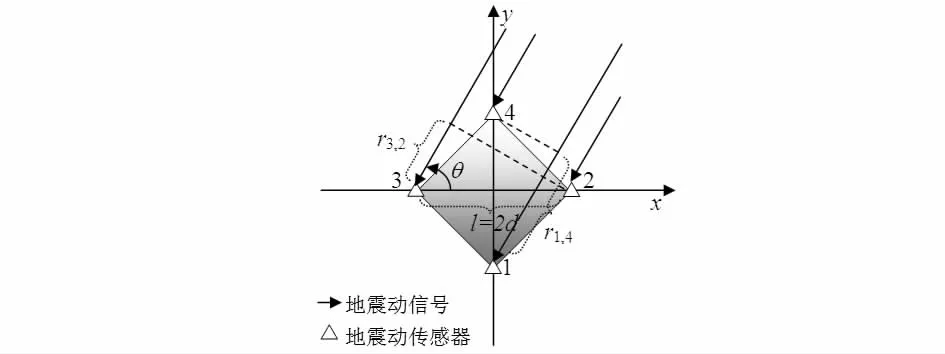
图2 四传感器方阵远距离目标定位Fig 2 Long distance target localization using four-sensor square array
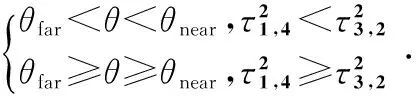
(5)
其中
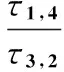

令两边界相减,并将knear用kfar表示,得到目标方位角估计带的带宽表达式
dθ=|θnear-θfar|=
(6)
解得目标方位角估计带的最大带宽
max dθ≈3.1650°.
(7)
由式(5)可知,对于一组给定时延值,目标真实方位角总是位于估计带之内,因此,在时延足够精确的情况下,不论信号传播速度如何,四传感器方阵关于目标方位角的估计误差都不会超过这一最大带宽值,从而证明了在四传感器方阵下信号传播速度和目标方位角估计的弱相关性。
3 仿真与实验
3.1 信号传播速度对目标方位角估计的影响
首先建立一个二维平面仿真测试环境,并在原点处布置一如图1所示,大小为l=21/2m的四传感器方阵。假设目标真实方位角θ= 20°,真实信号传播速度v=200 m/s。令目标距离r在1~20 m之内呈整数变化,并每次计算精确时延值。然后让传播速度估计值v′在10~240 m/s之间以10 m/s的步长变化取值,并根据真实时延值和v′依次对所有目标定位点进行方位角估计,得到如图3所示结果。图中的两条实线为目标方位角估计带边界,每条虚线为一组方位角估计结果,虚线编号对应计算时所采用的传播速度估计值v′。
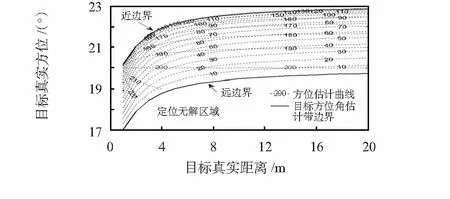
图3 信号传播速度对目标方位角估计影响曲线Fig 3 Curve of influence of signal propagation speed on target bearing estimation
从图中容易观察得出传播速度测量误差对定位结果的影响:当v′为一极小值时,目标方位估计的结果十分接近于远边界θfar;当传播速度逐渐增大,方位估计曲线也随之向上平移,直到在某一小于真实传播速度的v′处与近边界θnear重合,如本例中的130 m/s左右;随着v′的继续增大,曲线掉头向下,同时在近距离处收敛于目标真实方位角;整条曲线在传播速度测量值等同于真实值,即v′=v=200 m/s时变为一条恒等于真实目标方位角的直线;当v′大于真实的传播速度时,由于远边界θfar下方存在的定位无解区域而使得问题可能无实解。
3.2 时延误差对目标方位角估计的影响
在实际中,对信号时延的测量误差是不可避免的。由于目标方位角估计带的边界由时延确定,那么通过探讨时延误差与方位角估计带的关系便能间接得出其对目标方位角估计结果的影响。由方位角估计带边界的表达式(5)可知,这一问题的关键在于远边界θfar中两时延τ1,4和τ3,2的比值。在与之前相同的仿真测试环境下,已知9个预先设定的目标定位点坐标:(50,5),(40,10),(40,25),(25,10),(25,25),(10,25),(10,40),(25,40),(5,50)m。通过目标位置和真实传播速度可以计算出精确的时延值,然后对其加以20 %误差(θfar=0.8τ1,4/τ3,2),并以此计算目标方位角估计带边界,得到边界角度估计误差结果如表1所示。

表1 时延误差为20 %时边界角度估计误差Tab 1 Boundary angle estimation errors while time delay error is 20 %
表1中数据显示,远边界和近边界的方位角估计最大误差分别在7°和8°之内。由于目标方位角估计结果总是位于方位角估计带中,因而其估计误差也应介于两边界误差之间。由此可以预测,当时延误差在20%之内时,四传感器方阵目标方位角估计的最大误差在8°之内。
3.3 场地实验
在实际测试环境下设计了如下实验:在一块开阔平整的草地上布置一大小为l=21/2m的四地震动传感器方阵如图1所示,检测一人沿着以阵列为中心,半径10 m的圆圈行走的脚步信号。首先设地震动信号传播速度估计值为200 m/s,然后由式(4)得到目标方位角估计值,并由式(5)得到方位角估计带边界,其结果由图4所示。由图可知,四传感器方阵的目标方位角估计结果基本与实际情况相符,其平均估计误差3.43°远小于一般的三轴地震动传感器估计结果,由此证明了这一方法能够用于高精度的地震动目标方位角估计。
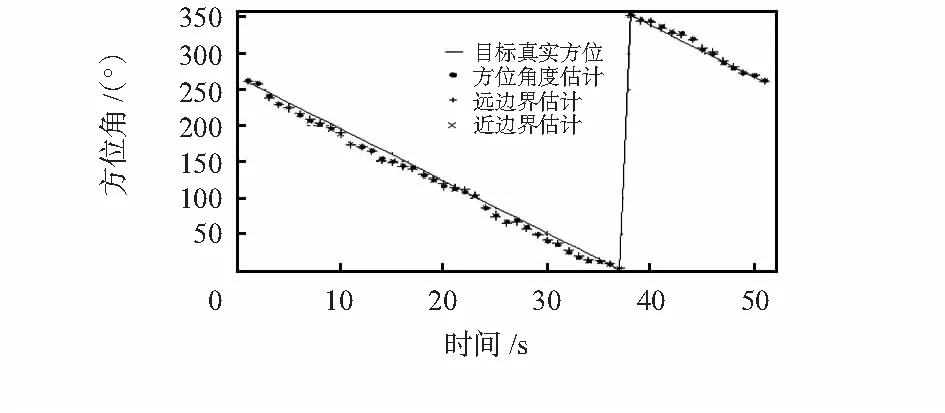
图4 人员走动目标方位角估计图Fig 4 Target bearing angle estimation of moving personnel
4 结 论
基于对四传感器方阵下目标方位角估计方法的研究,从理论上推导了目标方位角估计带并计算得出其最大理论带宽值为3.1650°,证明了这种阵列下信号传播速度与目标方位角估计之间的弱相关性。通过仿真计算分别探讨了信号传播速度和时延测量误差对目标方位角估计的影响。场地实验证明:四传感器方阵在实际应用中的目标方位角平均估计误差为3.43°,小于一般三轴地震动传感器的估计结果,因此,该方法适用于传播速度不定情况下的地震动目标测向定位。
[1] 朱庆厚.到达时间差( TDOA)测向定位研究[J].电讯技术,2007,47(1):53-56.
[2] 邓 平,李 莉,范平志.一种TDOA/AOA 混合定位算法及其性能分析[J].电波科学学报,2002,17(6):633-636.
[3] 仲祺琪,毛卫宁.利用DOA 的双基阵被动定位算法研究[J].声学与电子工程,2003,70(2):15-18.
[4] 陈 玲,李少洪.无源测向测时差定位算法研究[J].电子与信息学报,2003,25(6):771-776.
[5] 黄高明,杨绿溪,何振亚.基于典范相关分析的时差测向技术研究[J].电路与系统学报,2005,10(5):10-15.
[6] 李志宇,马昌萍.时延差优选估计声源定向算法[J].声学技术,2010,29(2):158-161.
[7] 黄国信,高 勇.四元传声器阵列定向算法及其结构优化[J].声学技术,2009,28(1):78-81.
[8] Yao K,Hudson R E,Reed C W,et al.Blind beamforming on a randomly distributed sensor array system[J].IEEE Journal on Selected Areas in Communications,1998,16:1555-1567.
[9] Zheng J,Lui K W,So H C.Accurate three-step algorithm for joint source position and propagation speed estimation[J].Signal Processing,2007,87:3096-3100.
[10] Chen J C,Yao K,Hudson R E.Source localization and beamfor-ming[J].IEEE Signal Processing Magazine,2002,19:30-39.
[11] Richman M S,Deadrick D S,Nation R J,et al.Personnel tracking using seismic sensors[C]∥Proc of the International Symposium on Aerospace/Defense Sensing,Simulation,and Controls,Orlando,USA,SPIE,2001:14-21.
[12] Pakhomov A,Sicignano A,Sandy M,et al.Single and three-axis geophone:Footstep detection with bearing estimation,localization,and tracking[C]∥Proc of Unattended Ground Sensor Technologies and Applications V,Orlando,USA:SPIE,2003:155-161.
[13] 张 磊.基于三轴地震动传感器的目标定向算法研究和硬件实现[D].南京:南京理工大学,2004.
[14] Knapp C,Carter G.The generalized correlation method for estimation of time delay[J].IEEE Transactions on Acoustics, Speech and Signal Processing,1976,24:320-327.
Seismic moving target bearing estimation based on four-sensor square array*
XIE Xiao, DONG Da-wei, HUA Chun-rong, YAN Bing
(School of Mechanical Engineering,Southwest Jiaotong University,Chengdu 610031,China)
A new approach in moving target bearing estimation based on time differences of arrival of seismic signals
at a four-sensor square array is proposed.The weak correlation between propagation speed of signals and bearing estimation under such sensor layout is exploited in theory,simple and explicit expressions of bearing margins as well as the maximum bearing estimation band range are deduced.Influence of signal propagation speed and time delay measurement errors on precision of bearing estimation is discussed according to simulation computation.It is eventually demonstrated through field experiment that this technique has a smaller bearing estimation error than the commonly used three-axis geophones and it has certain application value.
target bearing estimation; seismic moving signal; propagation speed; four-sensor square array
10.13873/J.1000—9787(2014)12—0042—03
2014—04—22
中央高校基本科研业务费专项资金资助项目(2682013CX020)
TN 971
A
1000—9787(2014)12—0042—03
谢 逍(1989-),男,四川成都人,硕士研究生,主要研究方向为地震动信号目标定位。

