姿态参数的模拟解算电路设计与分析*
王晓翠, 程为彬, 李 彬, 潘 萌
(西安石油大学 电子工程学院,陕西 西安 710065)
姿态参数的模拟解算电路设计与分析*
王晓翠, 程为彬, 李 彬, 潘 萌
(西安石油大学 电子工程学院,陕西 西安 710065)
根据姿态传感器输出与姿态参数之间的三角函数关系,设计了一种基于函数发生器的反三角函数电路,以减小模拟反三角函数解算误差,实现对姿态参数的直接解算。利用离散和连续2种方法对所设计电路进行测试,离散测试分析中采用多点拟合对实验数据进行处理,平均角度误差减小为0.11°,最大角度误差减小为2.87°;连续测试中对输入输出信号时域和频域特征进行了分析,测得输出波形的总谐波失真为8.14 %。结果表明:解算方案可行,可用于姿态参数的模拟解算。
模拟解算; 反正弦函数; 多点拟合; 频谱分析
0 引 言
在实时钻井中,井眼姿态参数对有效控制井眼轨迹起着至关重要的作用[1,2]。根据井下钻井工具姿态测量原理,三轴加速度计输出的是井斜角I、工具面角T和方位角A的三角函数关系[3],要得到姿态参数必须进行反三角函数的求解设计,求解方法有模拟求解和数字求解2种。数字求解反三角函数时,将数据直接输入单片机求解。若分辨率为1°时,双极性A/D的位数至少为14位,分辨率为0.5°时A/D的位数为16位,所以,数字求解对A/D的位数要求较高,同时要进行A/D转换、采样/保持等过程也会引入各种误差。而常见模拟反三角函数求解电路有2种方法:一是将反三角函数展开成级数,然后通过多次乘法和加法运算实现[4,5],函数展开成级数存在误差,且后续电路数据运算量大;二是利用余弦函数拟合电路或余弦函数电路与高精度运算放大器构成负反馈电路实现[6,7],这种方法的缺点是函数拟合时存在误差,而且实际中运算放大器的正负端电压并不完全相等。
为提高后续电路数据处理速度和解算精度,本文设计了一种能够直接实现姿态参数解算的电路。
1 模拟解算原理
根据三轴加速度计测量井眼轨迹的基本原理[7]可知,将重力加速度计向仪器坐标系投影,可以得出三轴加速度计的输出为[8]
(1)
由式(1)可知,要获得姿态参数,需对三轴加速度的输出进行解算。图1为2种工具面角模拟解算方案原理框图。
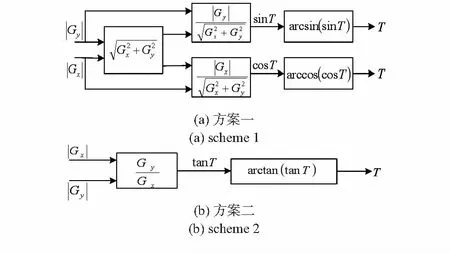
图1 工具面角模拟解算原理框图Fig 1 Principle block diagram of analog computation of tool face angle
井斜角可直接由模拟解算电路求解,当I′=90°-I时有
Gz=-gcosI=-gsinI′.
(2)
在工具面角T与井斜角I解算电路中都存在反正弦电路,本文以井斜角I为例,根据式(2)进行解算电路设计与测试分析。
2 模拟解算电路设计
AD 639是一种高精度单片函数转换器,通过引脚电压设置可以直接实现各种标准的三角函数和反三角函数,具有一致性好、转换速度快和谐波失真小等优点。
2.1 AD 639工作原理
根据AD 639内部原理框图,可知其最基本的功能函数为[9]

(3)
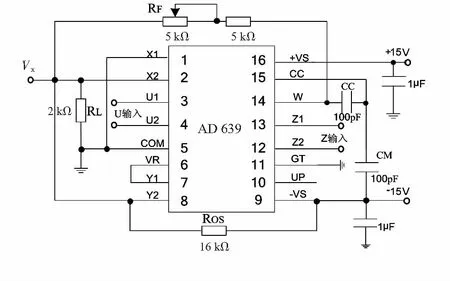
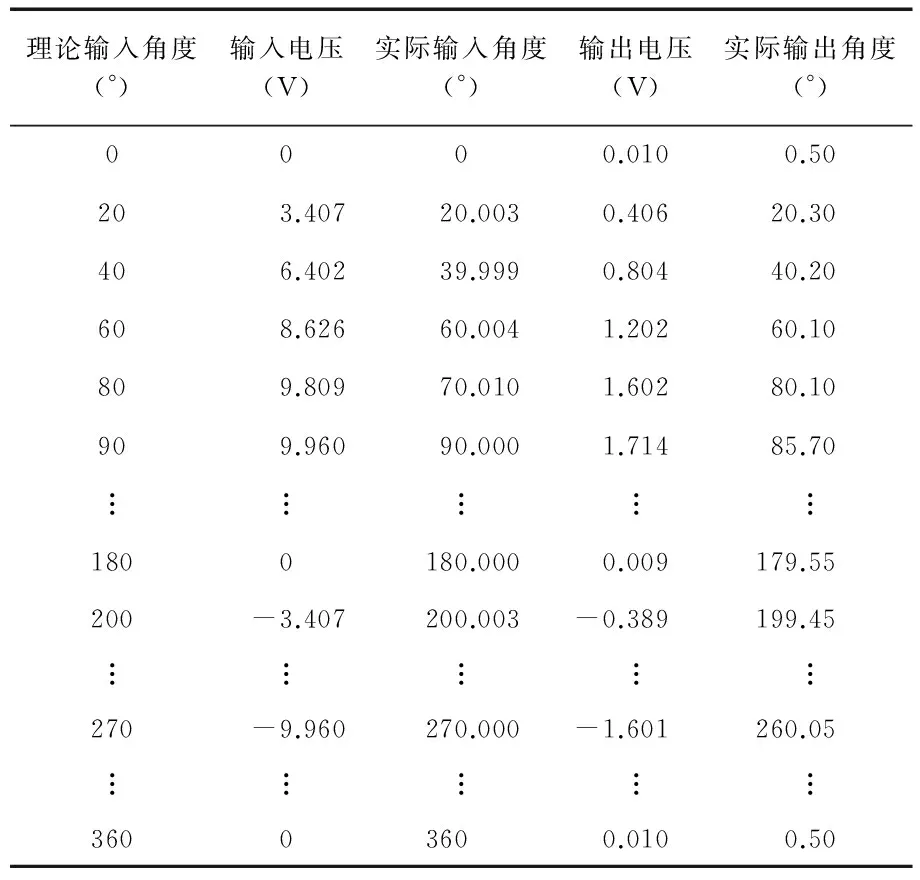
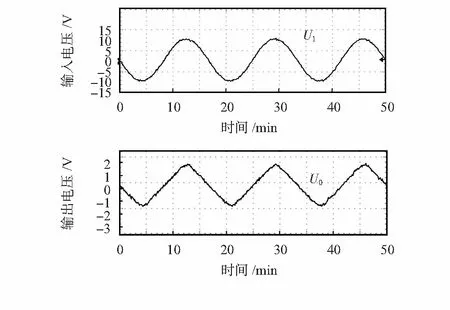
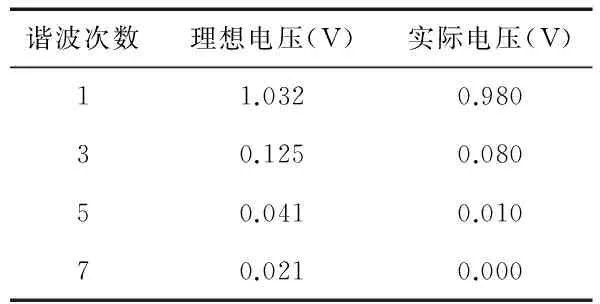
其中,AOL为输出放大器的开环增益(一般为85 dB);U=U1-U2+UP,U1,U2,UP为振幅控制电压,并且0 2.2 反正弦电路设计 要AD 639实现反函数模式,必须通过相应的正函数关闭输出放大器反馈环实现,则可得到 (4) AD 639的反三角函数模式中,应用最广泛的是反正切模式。将Z1,Z2端作为电路输入端,X2端作为电路输出端,即可实现2个差动模拟量比值的反正切运算,电路如图2所示。 图2 AD 639反正切工作方式Fig 2 Arctangent working mode of AD639 根据芯片各引脚电压值和式(4)可得 (5) 即 (6) 图2中CC和CM是为了实现相位补偿;ROS是为了补偿输入偏置电流,不会对I产生影响;RL是为了限制输出角度电压不超过±1.7 V(即±85°)。 反正弦电路与反正切电路连接方式相似。在反正弦电路中,CC和CM电容值可以减小或忽略。当Y2=0时,存在 (7) 则有 (8) 其具体的反正弦电路如图3所示。 图3 AD639反正弦工作方式Fig 3 Arcsine working mode of AD639 由式(2)可知, AD 639的反正弦工作方式可以实现对井斜角的直接模拟解算。 本文采用2种方法对解算电路进行测试分析:一种是离散测试分析,这种方法属于断点测量,并采用多点拟合对实验数据进行处理;另一种是连续信号频谱分析,既可测试电路解算精度,也可测试解算电路的实时响应性。 这种方法采用可调直流稳压电源输出作为电路的输入。电路幅度控制电压由引脚可编程的精密基准电压源提供,因为芯片精度问题,输出电压无法达到10 V,实际测量输出电压为9.960 V。由式(8)和图3可知,电路(Z1-Z2)端输入为9.960sinI时,电路输出为I。输入电压按9.960sinI计算得到,因为电路最大输出角度为85°,即1.7 V,在测试电路前电路输入9.960·sin 85°=9.922 V电压,调节RF使输出电压为1.7 V,输入角度I从0°开始逐渐递增至360°,步进间隔为5°,部分输出采样数据如表1所示。 表1 反正弦电路测试数据Tab 1 Test datas of arcsine circuit 3.1 数据分析 电路实验中,将理论输入角度对应下的输入电压保留到小数点后第三位作为电路的实际输入,所以,理论输入角度与实际的输入角度之间存在误差。在后续实验数据处理中,以实际的输入角度为基准进行计算,实验数据与误差曲线如图4所示。 在AD639的反函数模式中,X2端所接的2 kΩ电阻器是为了限制输出电压在±1.7 V(即±85°)之间,所以,电路在90°和270°附近存在饱和现象,这是反正切电路本身存在的问题,只能通过后续的数据处理减小误差。由实际输入角度与输出角度对比可看出:AD 639反正弦电路解算得到的角度值与理论角度值基本重合。角度误差曲线如图4(b)所示,平均角度误差为-0.19°,最大角度误差为-9.95°。 从上面的分析可以看出,本研究所选取的3个变量,即智力资本、战略柔性和创新能力的因子载荷基本满足要求;所设计调查问卷Cronbach系数都达到了0.7,说明因子变量基本符合要求,变量的描述性统计与相关性分析结果,如表4所示。 3.2 多点拟合 根据最小二乘原理,利用Matlab对实验数据进行拟合,得到拟合折线方程为 (9) 其中,y为电路实际输出电压值,x为实际输入电压对应的角度值。 将拟合折线计算得到的输出角度绘制曲线如图5(a)所示,误差如图5(b)所示。 图5 计算得到的输出角度与误差曲线Fig 5 Curves of calculated output angle and error 对比图4和图5可知,折线拟合得到的角度值的线性度比直接测量得到的角度值线性度好。经最小二乘法拟合处理的平均角度误差为0.11°,比直接测量的角度误差小。经过多点拟合法以后误差明显减小,最大角度误差为2.87°,比直接测量误差小。对于[0°,360°]之间的任意输入角度值,可以根据拟合折线方程计算得到对应的输出电压值。 这种方法采用连续信号作为电路的输入。在实时钻井中转盘的最高转速为300 r/min[10],即最高频率f为5 Hz,则姿态传感器的输出信号最高频率为5 Hz。实验电路中采用60 Hz信号对电路进行验证。 4.1 波形测试 当电路输入信号频率f为60 Hz、峰峰值电压VPP为19.92 V的正弦波时,理论输出应该为 arcsin(9.960sinx/9.960)=(-1)k(I-kπ). (10) 其中, (I-kπ) ∈[-π/2,π/2]。电路输出为电压值,按电压值与角度值之间的标度因数为20 mV/(°)计算,可知电路理论输出波形应为频率f为60 Hz、峰峰值电压VPP为3.6 V的三角波,电路实际输入输出波形采用TDS430A直接测量,波形如图6所示。 图6 实际输入输出波形图Fig 6 Waveforms of actual input and output 实际输出三角波频率f为60 Hz、最大电压为1.740 V,与理论波形基本吻合,也可以看出三角波在峰值处存在失真现象,即电路在90°和270°附近存在饱和现象。在90°时输出波形幅度相对误差为3.33 %。 4.2 时频分析 对频率f为60 Hz、峰峰值电压VPP为3.6 V的三角波进行仿真,得到傅里叶分析如图7(a)所示,实际输出三角波傅里叶分析如图7(b)所示。 图7 波形傅里叶分析Fig 7 Fourier analysis for waveforms 图7(a)中各次谐波的电压值为最大值,而利用示波器测得的各次谐波电压值UP为有效值,将所有电压值转换为有效值,各次谐波电压值如表2所示。 表2 三角波各次谐波电压峰值表Tab 2 Harmonics voltage peak value of triangle wave 钻井工具姿态测量属于动态测量[11],所以,连续信号频谱分析更接近于实际测量。 本文利用AD 639实现钻井姿态参数井斜角的直接解算。采用2种方法对电路进行了验证,离散测试中利用多点拟合法处理实验数据平均角度误差为0.11°,解算电路最大角度误差为2.87°;连续测试验证了电路的解算精度与实时响应性,电路输出波形总谐波失真为8.14 %,在90°时幅度相对误差为3.33 %。由于电路本身问题,在90°和270°附近误差较大,在90°和270°附近存在饱和现象。实验结果表明:解算方案可行,电路结构简单,实时性良好,可以实现姿态参数的模拟解算。 [1] 葛 亮,胡 泽,陈 平.井下工程参数随钻测试系统设计[J].传感器与微系统,2013,32(8):105-107. [2] 苏 毅,齐 昕,刘 阳,等.基于陀螺仪的随钻姿态测量新算法[J].传感器与微系统,2013,32(1):137-140. [3] 陈 琳.垂直钻井工具小角度姿态测量技术研究[D].西安:西安石油大学,2009. [4] 郑 勇,汉泽西,付鑫生,等.井姿态参数的工程算法设计[J].西安石油学院学报,1993,8(1):44-49. [5] 乐识非.陀螺罗盘定向测量中工具面角计算方法探讨[J].西安石油学院学报:自然科学版,2001,16(4):68-71. [6] 陈 琳,程为彬,郭颖娜,等.基于井下姿态测量的余弦函数模拟求解电路设计[J].电子器件,2009,32(1):104-107. [7] 周云凤.旋转导向钻井工具全角度姿态测量与解算技术研究[D].西安:西安石油大学,2010. [8] 张明菊,王 鹏,程为彬,等.旋转导向钻井工具姿态参数的模拟解算[J].西安石油大学:自然科学版,2009,24(4):54-59. [9] AD 639 Datasheet[DB/OL].1999—10—01.http:∥www.analog.com. [10] 邓忠彬,王 涛,王幼平.海洋钻井多参数仪系统设计研究[J].石油矿场机械,2010,39(7):54-59. [11] 王新宇.井斜动态测量理论与实验研究[D].武汉:武汉科技大学,2007. Design and analysis of analog computation circuit of attitude parameter* WANG Xiao-cui, CHENG Wei-bin, LI Bin, PAN Meng (School of Electronic Engineering, Xi’an Shiyou University,Xi’an 710065,China) According to trigonometric function relations between output of attitude sensors and attitude parameters,an inverse trigonometric function circuit based on function generator is designed,to reduce computation error of analog inverse trigonometric and realize directly computation of attitude parameters.Tests on the designed circuit with discrete and continuous methods are realized,in discrete test analysis,multi-point fitting is adopted to process experimental data,and the average angle error is reduced to 0.11° and the maximum angle error is reduced to 2.87°;in continuous measurement,features of the input and output signals in time-domain and frequency-domain are analyzed,total harmonics distortion of output waveform is 8.14 %.Experimental results show that the computation scheme is feasible,thus it can be used for analog computation of attitude parameters. analog computation; arcsine function; multi-point fitting; spectrum analysis 2013—10—09 国家自然科学基金资助项目(61174191);陕西省工业攻关计划资助项目(2011K06—27) TE 243; TP 274.2 A 1000—9787(2014)04—0072—04 王晓翠(1989-),女,陕西三原人,硕士研究生,主要研究方向为石油工程测试技术与仪器。

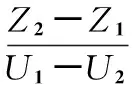

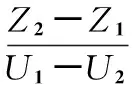
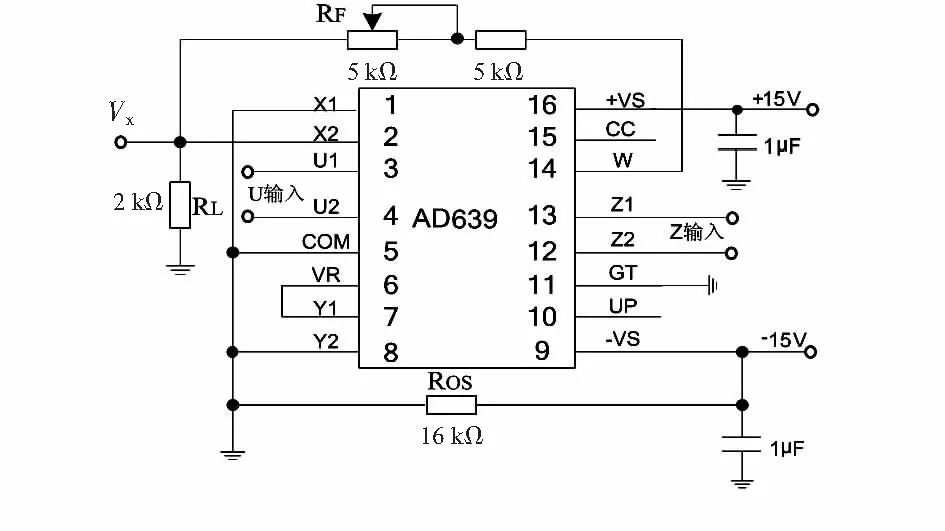
3 离散测试与分析


4 连续信号频谱分析
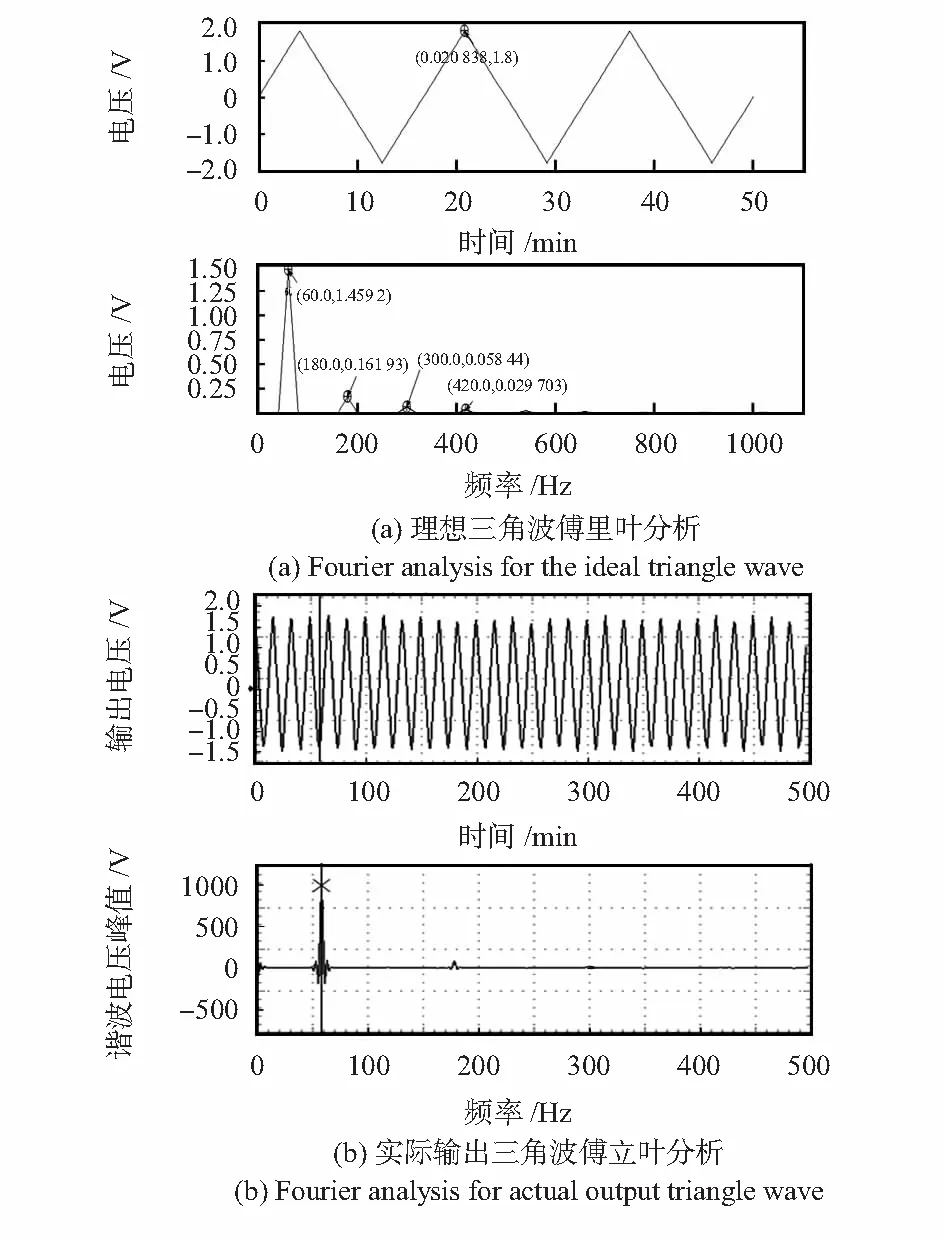
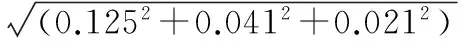
5 结 论

