基于ANSYS有限元法的电导率传感器分析*

陆贵荣， 吴玉晓， 陈树越

(1.常州大学 信息科学与工程学院，江苏 常州 213164；2.常州市过程感知与互联技术重点实验室,江苏 常州 213164)

基于ANSYS有限元法的电导率传感器分析*

陆贵荣1,2， 吴玉晓1， 陈树越1,2

(1.常州大学 信息科学与工程学院，江苏 常州 213164；2.常州市过程感知与互联技术重点实验室,江苏 常州 213164)

提出了一种结构简单的新型非接触电导率传感器。从原理出发，采用ANSYS有限元方法，通过建立有限元模型、定义材料属性、网格划分、设置边界条件、加载和求解等，得到了溶液电导率分别与传感器电感和电容之间的关系。利用该传感器对几种已知电导率溶液进行了测试，结果显示其测量的最大相对误差为0.64 %,从而证明所提出的传感器测量方法不仅测量精度可行，还提高了测量的冗余度和可靠性，具有很高的商业应用价值。

电导率传感器； 有限元法； 电容； 电感； 非接触检测

0 引 言

无论是在实验室还是工业领域，电解质溶液电导率的测量变得越来越重要。常用测量方法是将传感器的两电极直接与被测溶液接触，通过两电极间的电阻变化来测得溶液的电导率。这种方法不但测量范围窄，只能适用于测量比较纯净的水，而且对杂质多、腐蚀性强的液体，电极极可能被腐蚀，影响测量结果[1]。在这种情况下，非接触式电导率传感器就被提了出来，也有人研究了它的结构与测量方法[2～4]。比如:邱善乐设计的新型感应式电导率传感器，将2个线圈分别缠绕在2个磁环上，构成初级线圈与次级线圈，在其周围产生交流感应电动势，通过取压电阻器可以取到交流电压，从而根据该信号和电解液电导率之间的函数关系计算出溶液的电导率值[4]。由于这一类传感器弥补了传统测量方法的不足，得到了广泛的应用。

本文提出了一种结构简单的非接触式电导率传感器，有别于现有的非接触式电导率传感器的结构与原理，所提出的传感器利用2种方式，即电感和电容方式来同时评价未知溶液的电导率，结果显示，不但溶液的电导率得到了很好的评价，而且测量的冗余度和可靠性也得到了很大的提高。

1 结构与工作原理

本文提出的非接触电导率传感器的结构如图1所示，线圈密集地缠绕在塑料管1上，且紧密外套一个塑料管2，避免被测电解质溶液和线圈直接接触，塑料管3外套一个不锈钢管，其主要作用是和线圈构成电容传感器两电极板；在塑料管1内和塑料管2外与塑料管3内之间的空间注满被测溶液。

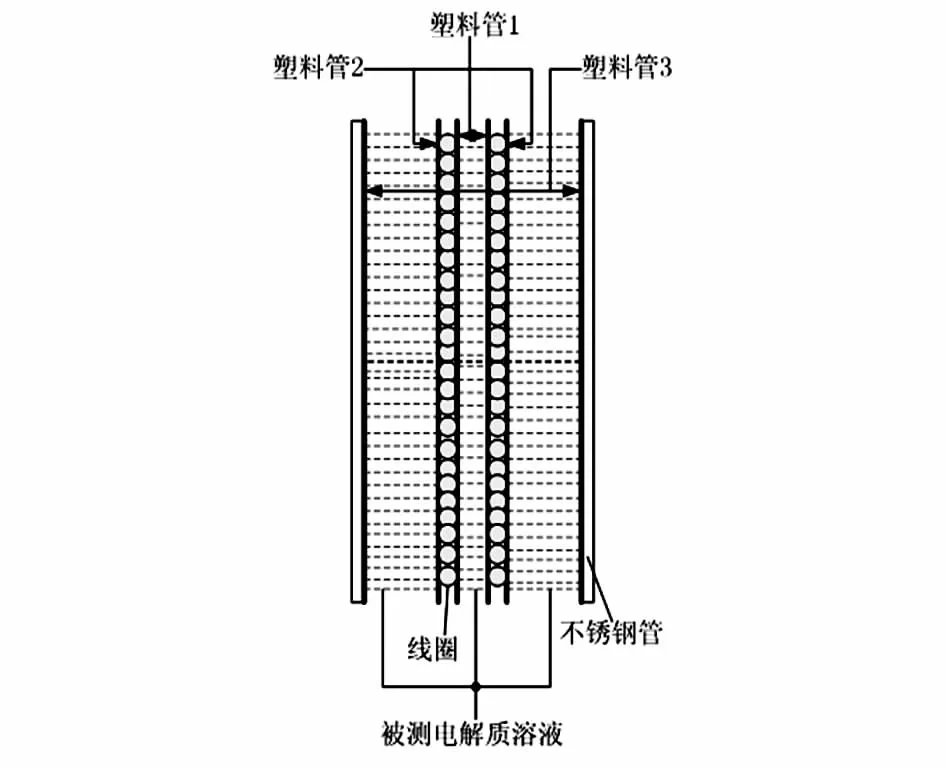
图1 传感器结构示意图Fig 1 Structure diagram of sensor

1.1 电容测量方式

当被测溶液流入塑料管2外和塑料管3内之间的空间时，线圈和不锈钢管组成的电容器极板之间的电解质介电常数发生改变，引起了它们之间的电容变化。这种电容的变化与被测电解液的电导率存在函数关系，因此，被测电解液的电导率信息被检测。电容值和电导率之间的关系可用如下的二次多项式来拟合

D(C)=β0+β1C+β2C2，

(1)

式中D为被测电解液的电导率，C为线圈和不锈钢的之间的电容；β0,β1,β2为系数，它们可利用各种已知电导率Dk(k=0,1,2,…,n)的电解液及其对应被测电容值Ck(k=0,1,2,…,n)之间的实验数据库回归计算得到，具体可由最小二乘曲线拟合方法计算如下：

假设实验过程中取n+1个观测数据点(Ck,Dk),k=0,1,2,…,n，则观测数据与拟合曲线式(1)偏差的平方和为

再由

解得β0,β1,β2。

1.2 电感测量方式

被测溶液是电解液，具有导电性，因此,当线圈通以高频交变的电流激励时，在线圈的周围就产生了交变磁场，电解液在该磁场范围内，在电解液中便产生了涡流,该涡流产生的反磁场又会抵削部分原磁场，就造成线圈电感量发生变化。线圈的电感随着被测溶液电导率的变化而改变，电感和电导率之间的函数关系同样可用实验的方法回归分析得到，从而电导率信息被评价。它们之间的关系可用如下的二次多项式来拟合

D(L)=α0+α1L+α2L2,

(2)

式中D为被测电解液的电导率，L为线圈的电感，α0,α1,α2为系数。它们也可利用各种已知电导率Dk(k=0,1,2,…,n)的电解液及其对应被测电感值Lk(k=0,1,2,…,n)之间的实验数据库回归分析，具体可由和上述类似的最小二乘曲线拟合方法计算得到。

2 ANSYS有限元分析

ANSYS软件可以进行各种分析，例如：结构分析、流体分析、电场分析、磁场分析、声场分析等[5]。根据传感器的结构和研究分析需要，这里考虑在二维电场和磁场2种情况下进行分析。虽然所有的物体都是三维的，但是在实际理论计算时首先考虑将它简化为二维平面问题或轴对称问题[6]。有实验结果说明,三维和二维建模方法均有效，只是模型的简化会使结果产生误差，但这误差均在工程允许的范围内[7]。由图1传感器结构示意图得知其为轴对称问题，所以，将其简化为二维模型进行有限元分析是完全可行的。

2.1 有限元模型的建立

根据图1所示传感器的结构，设计了电导率传感器有限元模型图，如图2。因为该电导率传感器为轴对称结构，所以，只取图形的一半进行建模。其中，A1和A5为被测电解液，A3为线圈，A7为不锈钢，A2，A4和A6为塑料管。

图2 传感器有限元模型图Fig 2 FEM diagram of sensor

1)定义单元类型

在二维谐波电磁场分析中，PLANE53多用于二维(平面和轴对称)磁场问题的建模，因此,用PLANE53来定义传感器有限元模型图中的各个面，但每个面所需单元类型的自由度不同。比如：要给线圈输入交变激励电压，需要耦合线圈所在区域所有节点的电流自由度，则其单元类型自由度为AZ,CURR；要在被测电解质溶液中显示电涡流的分布，则其单元类型自由度为AZ,CURR,EMF；塑料管和不锈钢，则只需选用AZ自由度[8]。

2)定义材料属性

线圈用铜线绕成，塑料管和不锈钢管采用普遍使用的材料。这3种介质的相对磁导率μr、常温下的电阻率ρ等材料属性参数见表1。

表1 材料属性参数表Tab 1 Property parameters of materials

注：真空中的磁导率μ0=4×10-7H/m

3)定义实常数

线圈需通过定义实常数来表示其几何形状和绕组特性，包括线圈的截面面积(CARE)、线圈的总匝数(TURN)和导电线圈的填充因子(FILL)。

4)网格划分

ANSYS提供了延伸划分、映射划分、自由划分和自适应划分4种网格划分方法。 分析中所使用模型为规则几何图形，可采用映射网格划分[9]。

2.2 定义边界条件

ANSYS通常使用2种边界条件，第一类边界条件——Dirichlet条件(Az约束)：磁通量平行于模型边界；第二类边界条件——Neumann条件(自然边界条件)：磁通量垂直于模型边界。根据模型的特点和分析需要，加载第一类边界条件[9]。

2.3 求 解

给线圈加交变电压15 V，选择谐波HARMONIC分析类型，并设置分析频率和载荷步，然后求解。

3 仿真结果

3.1 电磁场磁力线分布图

该模型中，线圈的内半径、外半径的取值分别为5.2，5.6 mm，整个模型的高为60 mm。

在ANSYS后处理器中，可观察到模型中电磁场磁力线分布图，如图3所示。从图中可以看出:其分布规律与理论分析结果[8]相符，说明该文对传感器结构所做的简化为二维模型是合理的。

图3 电磁场磁力线分布图Fig 3 Distribution lines of magnetic force of electromagnetic field

3.2 电感、电容分别与电导率之间的关系

通过理论分析可知，当溶液电导率不同时，从传感器得到的电感和电容值不同。在电场和磁场分析中，对表示被测液体的面A1和A5赋于不同材料属性，即不同的电导率属性，求解计算得到不同的电感和电容值；再将溶液电导率分别与对应的电感、电容值用最小二乘法拟合，得到了电感、电容分别与电导率之间的关系图及其关系式。

图4为在电磁场分析中，不同浓度的电解质溶液下，线圈的电感与电导率之间的关系图。理论分析可知，溶液电导率越大，产生的涡流就越大，对通以交变激励电流的线圈所产生的原磁场消减的就越多，因此，线圈的电感就会越小。从图中可以看出：随着溶液电导率的增加，电感值下降，这与理论分析相符。

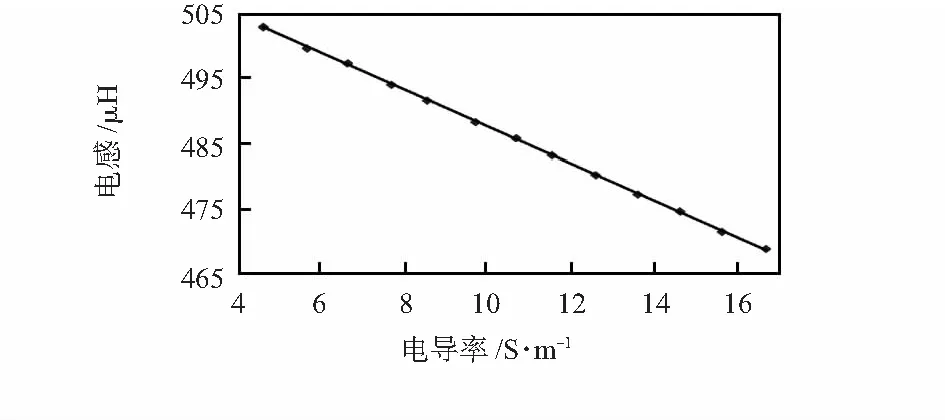
图4 溶液电导率与电感之间的关系Fig 4 Relationship between solution conductivity and inductance

用最小二乘法拟合，得到线圈的电感与电导率之间的线性关系式

σ=-0.351 2L+181.26.

(3)

图5为在电场分析中，不同浓度的电解质溶液下，线圈和不锈钢管之间的电容与电导率之间的关系图。理论分析可知，随着溶液电导率的变大，其介电常数变小[10]，而电容与介电常数之间同等变化，即介电常数变小，电容也变小，因此,当溶液电导率变大时，电容变小。从图中可以看出:随着溶液电导率的增加，线圈和不锈钢管之间的电容减小，与理论分析相符。

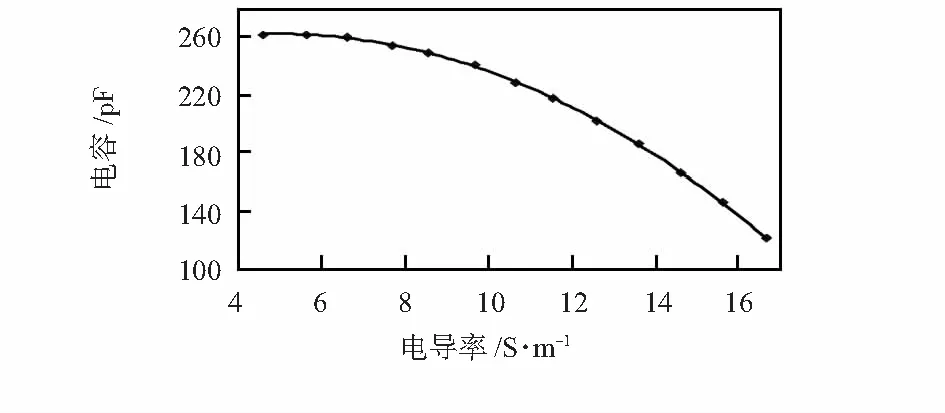
图5 溶液电导率与电容之间的关系Fig 5 Relationship between solution conductivity and capacitance

用最小二乘法拟合，得到电容和电导率之间的关系式

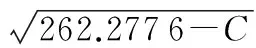
(4)

4 溶液电导率测试

为了验证仿真结果的可靠性，取3种已知电导率值的电解溶液分别注入传感器中，分别得到传感器的电感和电容值,再根据上述仿真结果中的2个关系式，计算得到溶液电导率值，然后将其与真实值做对比，结果如表2所示。

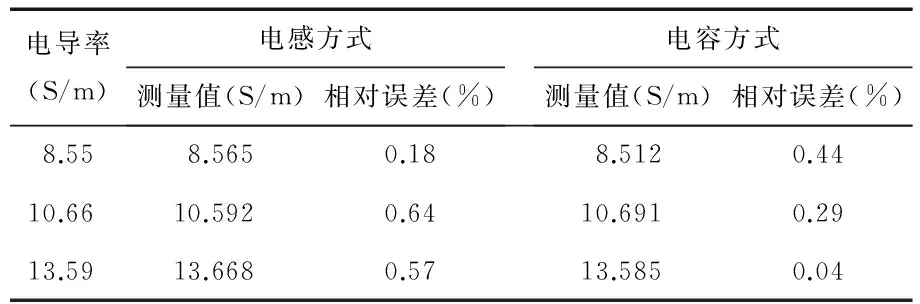
表2 传感器测试数据Tab 2 Test datas of sensor

从表中的测试数据结果看出:该传感器测量电导率的误差均在可接受的范围内，说明该传感器结构与测量原理的可行性，由于采用了2个独立的途径同时评价了电导率，从而提高了测量的冗余度和可靠性。

5 结 论

本文使用ANSYS有限元分析方法，通过建立有限元模型、定义材料属性、网格划分、设置边界条件、加载求解等，对被提出的非接触式电导率传感器结构和测量原理进行仿真分析，得到了溶液电导率分别与传感器输出电感和电容之间的关系。从测试结果中可知,该传感器测量电导率的最大相对误差是0.64 %,说明被提出的非接触式电导率传感器的原理是可行的，与目前已有的非接触式传感器相比，不仅很好地评价了溶液电导率，还提高了测量冗余度和可靠性，为传感器的制造提供了非常重要的理论指导。

[1] 陈培杰，汪志云.用自制非接触式液体电导率传感器测量液体的电导率[J].科技信息，2008(7):96-98.

[2] Ismail Abu Bakar Md,Shida Katsunori.Estimation of electrolytic concentration in aqueous solution with higher accuracy using electromagnetic multifunctional sensing[J].Sensors and Actuators A,2003，102:205-209.

[3] Kub P,Hauser P C.A review of the recent achievement in capacitively coupled contactless conductivity detection[J].Analytica Chimica Acta,2008,607(1):15-29.

[4] 邱善乐.一种新型感应式电导率传感器的设计[J].录井工程,2005,16(3):48-50.

[5] 王春兰，张 钢，董鲁宁，等.电涡流传感器的有限元仿真研究与分析[J].传感器与微系统,2006,25(2):41-46.

[6] 胡仁喜，孙明礼.ANSYS 13.0电磁学有限元分析从入门到精通[M].北京:机械工业出版社,2012.

[7] 于亚婷，杜平安.与被测材料无关的电涡流传感器基础理论与实现方法研究[D].成都：电子科技大学,2007.

[8] 于亚婷.电涡流传感器的电磁场仿真分析[D].成都：电子科技大学,2005.

[9] 杨 磊，韩邦成，孙津济.基于Ansys有限元法的电涡流位移传感器分析[J].传感器与微系统,2007,26(10):15-17.

[10] 高 悦，杨国胜，王 华，等.蒸馏水和NaCl溶液复介电常数的测量及修正[J].生物医学工程学杂志,2005,22(3):548-549.

Analysis of conductivity sensor based on FEM by ANSYS*

LU Gui-rong1,2, WU Yu-xiao1, CHEN Shu-yue1,2

(1.School of Information Science and Engineering,Changzhou University,Changzhou 213164,China;2.Key Laboratory for Process Perception and Interconnected Technology of Changzhou,Changzhou 213164,China)

A new type of non-contact conductivity sensor with simple structure is proposed.The relationship between solution conductivity with sensor inductance and capacitance can be obtained based on the theory and finite element method(FEM)by ANSYS,through setting up FEM,defining material property,meshing,establishing border conditions,loading,solving，and so on.Test on several known conductivity solution is carried out using the sensor,the results show that the maximum relative error of the measurement is 0.64 %,therefore it is proved that the proposed sensor measurement method not only has feasible measurement precision,but also improves measurement redundancy and reliability,and has high commercial application value.

conductivity sensor; finite element method (FEM); capacitance; inductance; non-contact detection

2013—09—30

国家自然科学基金项目资助 (51176016)

P 212

A

1000—9787(2014)04—0065—03

陆贵荣(1968-)，男，甘肃定西人，博士，副教授，主要研究方向为传感器技术与仪器仪表。