混合尺度聚类模型收敛性分析及仿真
王文庆, 薛 飞
(1.西安邮电大学 自动化学院, 陕西 西安 710121; 2.西安邮电大学 管理工程学院, 陕西 西安 710121)
混合尺度聚类模型收敛性分析及仿真
王文庆1, 薛 飞2
(1.西安邮电大学 自动化学院, 陕西 西安 710121; 2.西安邮电大学 管理工程学院, 陕西 西安 710121)
针对被分类对象属性多样性的客观实际,分析使用单一间隔尺度或名义尺度进行聚类的局限性,并提出一种混合尺度聚类模型。新模型以明氏距离及翻转距离为基础,引入混合尺度。利用下准则函数及逐步聚类算法可证新模型的收敛性。以某小区保安预警系统的采样数据为例,运用Matlab软件对新模型进行仿真验证,结果表明,新模型可应用于被分类对象具有多种特征属性的聚类问题。
混合尺度聚类;下准则函数;聚类收敛性
单一的间隔尺度或名义尺度聚类的研究已经非常深入[1-2]。但描述被分类对象的指标却非常的复杂、繁多,无论是间隔尺度指标还是名义尺度指标都无法完整的描述事物的特性。例如某一类物体具有如下指标(重量、数量、高度、形态、颜色、气味),要对其进行聚类,若用间隔尺度聚类,就会忽略形态、颜色、气味,若用名义尺度聚类就会忽略重量、数量、高度。这样,传统单一的间隔尺度或名义尺度聚类都不能满足人们对聚类的需求。因此,混合尺度(兼用间隔尺度和名义尺度)聚类就变得尤为重要。
文献[1]对名义尺度聚类问题进行了研究;文献[2]针对间隔尺度聚类提出了一种并行聚类算法,并使其构建在MapReduce并行框架上,以使得算法能够应用于大规模数据分类;文献[3]提到了混合聚类模型,但只对其做出了简单的理论说明,并未进行实际的证明;文献[4]提出判别模糊C-均值聚类算法以提高大样本数据的聚类速度;文献[5]主要讨论了聚类方法的发展状况,提出了基于有限维联合混合模型的聚类算法BGMMn;文献[6]给出了一种一般逐步聚类模型,并对其收敛性进行了证明;文献[7]提出了一种基于BIRCH算法的混合属性聚类算法;文献[8]对聚类分析进行了相关描述。
本文以文献[3,6]的研究工作为基础,着重分析混合尺度(间隔尺度和名义尺度相结合)聚类模型及其收敛性,并通过实际数据对模型进行仿真。文章提出的混合尺度聚类模型,就是要为人们在处理复杂事物时提供方便,把相似的事物更加精确的归为一类,差异较大的事物归在不同的类当中,以提高人们的工作或学习效率。
1 混合尺度聚类模型
设有
Y=P1,
Z=G1×G2×…×GP2,
其中
P1+P2=P
为描述被分类对象的指标数。P元变量
x=(y,z)T∈X
的前P1个分量y∈Y是间隔尺度变量,而后P2个分量z∈Z是名义尺度变量。以X表示所有的样品。设已取得N个样品
E={x1,x2,…,xN} (xi∈X),
为了消除量纲影响并使两种变量处于同等地位,假定其中各间隔尺度变量都已极差标准化,即以
(i=1,2,…,P;k=1,2,…,N)
(1)
代替原来的yik,将归一化后的E记为Λ,其中的样品记为
λ=(μ,ν)T∈Λ。
定义
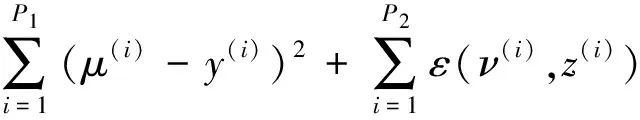
(2)
为描述两个样品各指标之间的距离,其中λ,x∈Λ为不同的样品,μ代表间隔尺度指标、ν代表名义尺度指标。
根据明氏(Minkowski)距离公式
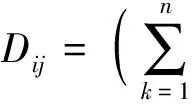
当q=2时,上式即为欧式距离
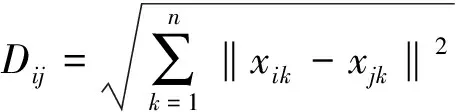

(3)
上式即为兼顾间隔尺度与名义尺度的混合尺度“距离”。以下将证明可作为聚类距离尺度。
2 收敛性分析
定义1(距离空间)[9]设C是某些元素组合的集合,如果对任何x,y∈C,按照一定的法则确定一个非负实数d(x,y),且满足
(ⅰ) 非负性:d(x,y)≥0, 且d(x,y)=0当且仅当x和y为C中同一个样本元素。
(ⅱ) 对称性:d(x,y)=d(y,x)。
(ⅲ) 三角不等式: 任给x,y,z∈C,有
d(x,y)≤d(x,z)+d(z,y)。
则d(x,y):C×C→2叫做C上的距离,C称为距离空间。
定义2(翻转距离) 名义尺度样本xi和xj之间的翻转距离|xi-xj|定义为xi=xj前的翻转次数。xi和xj的属性xik和xjk∈(k=1,2,…,n)。
事实上,根据Minkowski不等式
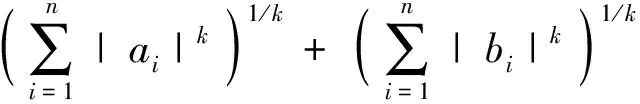
其中k≥1,ai,bi是实数或复数,可得
d(x,z)+d(z,y)。
3 算法仿真
某小区的保安预警系统,需要将门禁监控抓拍到的出入小区人员体貌特征,与近期公安系统发布的犯罪嫌疑人的体貌特征进行比对分析,以协助案件侦破并保证小区安全。这种人员体貌特征分析是一个典型的混合尺度聚类问题。为此,选取9个体貌特征数据{体重(kg),年龄(岁),身高(cm),性别,胖瘦,肤色,衣着,发型,脸型}进行聚类分析。其中,前三个特征属于间隔尺度,后六个特征属于名义尺度。对名义尺度做如下量化处理,如表1所示。

表1 名义尺度的量化
经一段时间采样获得数据如表2。
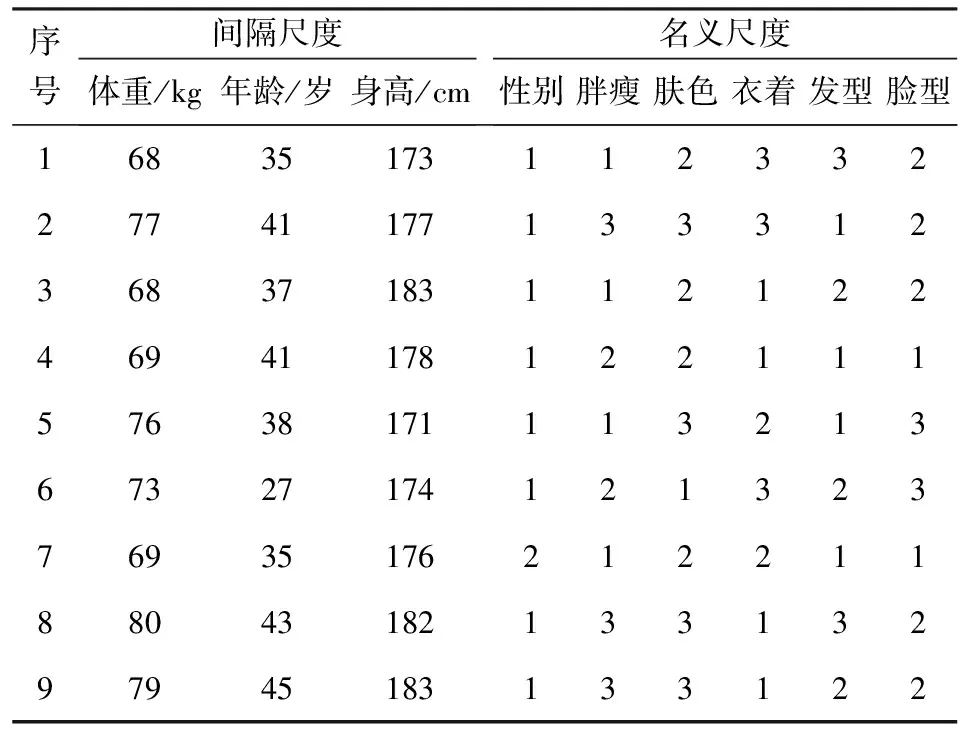
表2 采样所得原始数据
表2中的9号数据为公安系统发布的犯罪嫌疑人体貌特征,其余数据为采样获得的有待分析的数据。
应用聚类模型,具体步骤如下。
第1步 将间隔尺度转换为名义尺度,即体重:65~70kg用1替换,71~75kg用2替换,76~80kg用3替换;年龄:20~30 岁用1替换,31~40 岁用2替换,41~50 岁用3替换;身高:170~175cm用1替换,176~180cm用2替换,181~185cm用3替换。得出表3。
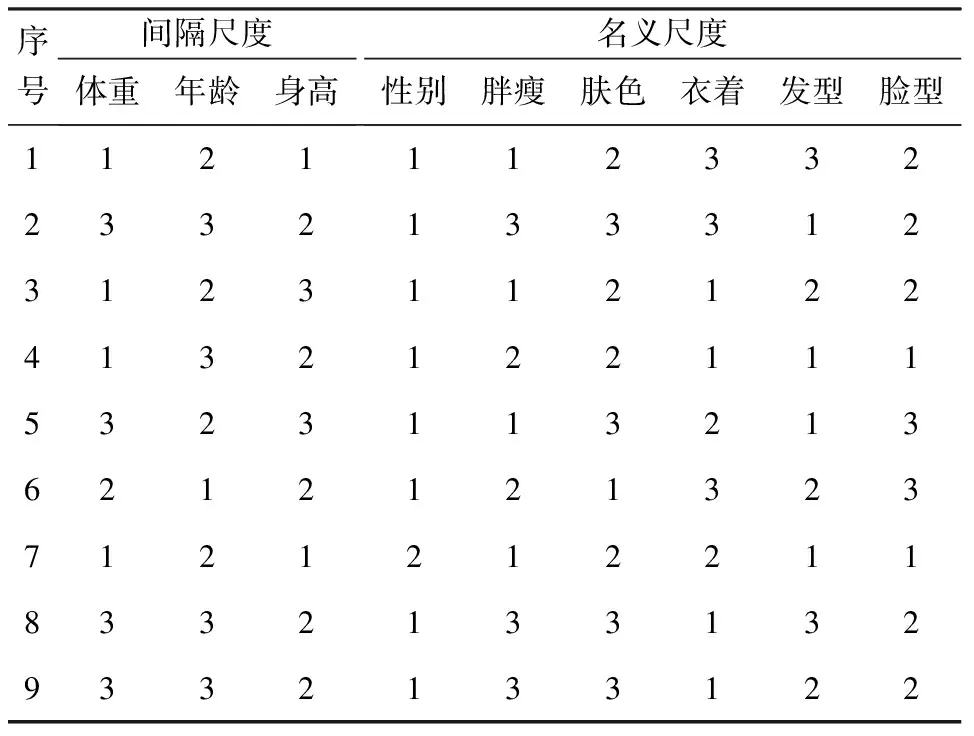
表3 间隔尺度转换为名义尺度后的数据
第2步 所有数据已转成名义尺度,用名义尺度的测量方法“翻转距离”对数据进行聚类。用Matlab软件对该例进行分析聚类[10](Matlab程序见附录),并输出聚类谱系图(图1)。
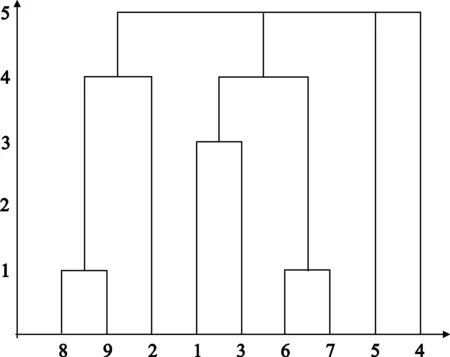
图1 Matlab聚类谱系图
用以聚类的Matlab程序流程如下。
(1) 判断每两行元素是否相同。
(2) 统计出不同元素的个数(数字越大距离越远)。
(3) 根据每两行之间的距离调用Matlab函数(dendrogram)画谱系图。
从聚类谱系图能够直观的得出8号数据与9号数据吻合度最高,可以确定8号数据对应的人员和公安系统所寻找的犯罪嫌疑人最为相似,所以8号应作为重点监控对象。
这里有几点需要特别说明。
(1) 将进、出小区人员体貌特征与犯罪嫌疑人体貌特征进行聚类分析,显然,这种聚类是一种混合尺度聚类问题,适合所提模型,所以能够验证该模型。
(2) 两种尺度的转换。把间隔尺度转换为名义尺度:给间隔尺度的某一取值范围附一变量作为名义尺度变量,名义尺度变量所代表的间隔尺度变量的取值范围可实时调节,以适应聚类的要求。(此类聚类中亦可将名义尺度变量转换为间隔尺度变量)。
(3) 不同需求的分类对各指标的侧重点要求不同,必要的情况下每个指标前还可以根据不同的需求附加不同的权值,以提高分类的实用性。
4 结 语
以前人的工作结果为前提,指出了传统的间隔尺度和名义尺度聚类已经不能满足日益发展的聚类需求,讨论了基于混合尺度(间隔尺度和名义尺度相结合)的聚类模型,证明了该模型的收敛性,用Matlab软件对论证了该模型实用性的实例进行了仿真。未来混合尺度聚类将会得到更广泛的应用,有关在间隔尺度和名义尺度之间转换的问题是本文今后继续研究的方向之一,以提高混合尺度聚类的有效性和实用性。
附录: 混合尺度聚类Matlab程序
A=[ 1 2 1 1 1 2 3 3 2
3 3 2 1 3 3 3 1 2
1 2 3 1 1 2 1 2 2
1 3 2 1 2 2 1 1 1
3 2 3 1 1 3 2 1 3
2 1 2 1 2 1 3 2 3
1 2 1 2 1 2 2 1 1
3 3 2 1 3 3 1 3 2
3 3 2 1 3 3 1 2 2]
t12=0;t13=0;t14=0;t15=0;t16=0;t17=0;t18=0;t19=0;
t23=0;t24=0;t25=0;t26=0;t27=0;t28=0;t29=0;
t34=0;t35=0;t36=0;t37=0;t38=0;t39=0;
t45=0;t46=0;t47=0;t48=0;t49=0;
t56=0;t57=0;t58=0;t59=0;
t67=0;t68=0;t69=0;
t78=0;t79=0;
t89=0;
for i=1
for j=1:9
n=i+1;
if A(i,j)~=A(n,j)
t12=t12+1;
end
end
for j=1:9
n=i+2;
if A(i,j)~=A(n,j)
t13=t13+1;
end
end
for j=1:9
n=i+3;
if A(i,j)~=A(n,j)
t14=t14+1;
end
end
for j=1:9
n=i+4;
if A(i,j)~=A(n,j)
t15=t15+1;
end
end
for j=1:9
n=i+5;
if A(i,j)~=A(n,j)
t16=t16+1;
end
end
for j=1:9
n=i+6;
if A(i,j)~=A(n,j)
t17=t17+1;
end
end
for j=1:9
n=i+7;
if A(i,j)~=A(n,j)
t18=t18+1;
end
end
for j=1:9
n=i+8;
if A(i,j)~=A(n,j)
t19=t19+1;
end
end
end
for i=2
for j=1:9
n=i+1;
if A(i,j)~=A(n,j)
t23=t23+1;
end
end
for j=1:9
n=i+2;
if A(i,j)~=A(n,j)
t24=t24+1;
end
end
for j=1:9
n=i+3;
if A(i,j)~=A(n,j)
t25=t25+1;
end
end
for j=1:9
n=i+4;
if A(i,j)~=A(n,j)
t26=t26+1;
end
end
for j=1:9
n=i+5;
if A(i,j)~=A(n,j)
t27=t27+1;
end
end
for j=1:9
n=i+6;
if A(i,j)~=A(n,j)
t28=t28+1;
end
end
for j=1:9
n=i+7;
if A(i,j)~=A(n,j)
t29=t29+1;
end
end
end
for i=3
for j=1:9
n=i+1;
if A(i,j)~=A(n,j)
t34=t34+1;
end
end
for j=1:9
n=i+2;
if A(i,j)~=A(n,j)
t35=t35+1;
end
end
for j=1:9
n=i+3;
if A(i,j)~=A(n,j)
t36=t36+1;
end
end
for j=1:9
n=i+4;
if A(i,j)~=A(n,j)
t37=t37+1;
end
end
for j=1:9
n=i+5;
if A(i,j)~=A(n,j)
t38=t38+1;
end
end
for j=1:9
n=i+6;
if A(i,j)~=A(n,j)
t39=t39+1;
end
end
end
for i=4
for j=1:9
n=i+1;
if A(i,j)~=A(n,j)
t45=t45+1;
end
end
for j=1:9
n=i+2;
if A(i,j)~=A(n,j)
t46=t46+1;
end
end
for j=1:9
n=i+3;
if A(i,j)~=A(n,j)
t47=t47+1;
end
end
for j=1:9
n=i+4;
if A(i,j)~=A(n,j)
t48=t48+1;
end
end
for j=1:9
n=i+5;
if A(i,j)~=A(n,j)
t49=t49+1;
end
end
end
for i=5
for j=1:9
n=i+1;
if A(i,j)~=A(n,j)
t56=t56+1;
end
end
for j=1:9
n=i+2;
if A(i,j)~=A(n,j)
t57=t57+1;
end
end
for j=1:9
n=i+3;
if A(i,j)~=A(n,j)
t58=t58+1;
end
end
for j=1:9
n=i+4;
if A(i,j)~=A(n,j)
t59=t59+1;
end
end
end
for i=6
for j=1:9
n=i+1;
if A(i,j)~=A(n,j)
t67=t68+1;
end
end
for j=1:9
n=i+2;
if A(i,j)~=A(n,j)
t68=t68+1;
end
end
for j=1:9
n=i+3;
if A(i,j)~=A(n,j)
t69=t69+1;
end
end
end
for i=7
for j=1:9
n=i+1;
if A(i,j)~=A(n,j)
t78=t78+1;
end
end
for j=1:9
n=i+2;
if A(i,j)~=A(n,j)
t79=t79+1;
end
end
end
for i=8
for j=1:9
n=i+1;
if A(i,j)~=A(n,j)
t89=t89+1;
end
end
end
w=[t12 t13 t14 t15 t16 t17 t18 t19 t23 t24 t25 t26 t27 t28 t29 t34 t35 t36 t37 t38 t39 t45 t46 t47 t48 t49 t56 t57 t58 t59 t67 t68 t69 t78 t79 t89] %翻转距离
B=squareform(w) %构成矩阵
Z = linkage(w); % 最短距离法
T = cluster(Z,5); %等价于 { T=clusterdata(X,3) }
find(T==3); % 第3类集合中的元素
[H,T]=dendrogram(Z); % 画聚类图
[1] 许洪波,卜东波,白硕.一种针对名义尺度变量的优化聚类算法[J].微电子学与计算机,2003(12):11-15.
[2] 卜东波.聚类分类理论研究及其在文本挖掘中的应用[D].北京:中国科学院计算机研究所,2000:22-35.
[3] 赵平.建设工程项目总承包风险管理研究[D].西安:西北工业大学,2010:31-40.
[4] 支晓斌,田溪.判别C-均值模糊聚类法[J].西安邮电大学学报,2013,18(5):26-30.
[5] 刘洋.基于混合模型聚类的方法[D].长春:东北师范大学,2010:30-37.
[6] 周光亚.逐步聚类的一般模型及其收敛性[J].吉林大学学报,1978(1):47-56.
[7] 李贤.混合属性聚类算法研究[D].长沙:长沙理工大学,2010:28-35.
[8] 何晓群.多元统计分析[M].3版.北京:中国人民大学出版社,2012:57-83.
[9] 李广民.应用泛函分析原理[M].西安:西安电子科技大学出版社,2003:35-42.
[10] 张继生,白秋颖.C语言程序设计[M].2版.北京:清华大学出版社,2011:127-186.
[责任编辑:王辉]
Convergence analysis and simulation of mixed-scale clustering model
WANG Wenqing1, XUE Fei2
(1. School of Automation, Xi’an University of Posts and Telecommunications, Xi’an 710121, China; 2. School of Management Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)
In order to classify the objectives with complex attributes, a novel mixed-scale clustering model is proposed after analyzing the limitation of both interval scales and nominal scale for clustering. This model is based on Minkowski’s distance and flip distance, and its convergence is proved with under criterion function and stepwise-clustering algorithm. Sample data collected form a security early-warning system of neighborhoods is used to verify the model with Matlab software. The results show that the model is valid to classify the objectives with complex attributes.
mixed-scale clustering, under criterion function, cluster convergence
10.13682/j.issn.2095-6533.2014.03.012
2014-03-08
国家自然科学基金资助项目(61305098)
王文庆(1964-),男,教授,从事智能信息处理研究。E-mail: wwq@xupt.edu.cn 薛飞(1986-),男,硕士研究生,研究方向为信息管理。E-mail: xuefeifei.good@163.com
TP301.6
A
2095-6533(2014)03-0058-06

