新型动摩擦实验装置的验证
卢玉斌 李 科 滕 骁
(西南科技大学制造过程测试技术教育部重点实验室 四川绵阳 621010)
在许多实验测试中滑动摩擦是不可忽略的,如在基于分离式霍普金森压杆(SHPB)进行材料的力学性能测试实验中,需要考虑SHPB压杆与试样端面之间的滑动摩擦,否则会引起测试结果的误差[1-2]。
如今在工程上有多种测试动摩擦系数的装置,但这些动摩擦系数测试装置所能达到的相对滑动速度大多局限于2.5 mm/s-2.54 m/s。利用这些装置研究冲击加载条件下较宽范围内的相对滑动速度对动摩擦系数的影响却很困难[3-5]。因此,笔者基于文献[6]设计了一套动摩擦试验装置,用于测量相对滑动速度在10 m/s以内的动摩擦系数,并且在材料的更换上更加简单方便。
笔者设计的动摩擦实验装置如图1所示。滑块在斜面上滑下,加速度计安装在加载重物上,可实时记录滑块的加速度,由斜面倾角和滑块加速度可计算得到动摩擦系数,以实现间接测量不同材料之间的滑动摩擦系数[7]。该实验装置具有构造简单、使用方便、适应性强等特点。在该实验装置中可以更换材料一和材料二,这样就可测试任意2种材料之间的滑动摩擦系数。并且该装置可以调节滑板和地面的角度以调节2种材料的相对滑动速度,从而可用于测量相对滑动速度在10 m/s以内的动摩擦系数。加速度计采用KISTLER 8303A1型,其技术参数如表1所示。基于该实验装置所测得的不同材料之间的动摩擦系数可用于修正SHPB测试中试样与压杆之间滑动摩擦产生的影响。

表1 KISTLER 8303A1加速计的技术参数[6]Table 1 The Technical parameters of KISTLER 8303A1 accelerometer[6]

图1 滑动摩擦试验装置模型Fig.1 The schematic of kinematic friction set- up
动摩擦实验中需要测量多种材料之间的滑动摩擦系数,更换材料需要花费较长时间,但在数值模拟中可避免这样的问题,更改材料属性即可更换材料,使测试过程快速高效,得到的加速度数据易于处理。本文将采用有限元商业软件ABAQUS对动摩擦实验装置的可靠性和实用性进行数值模拟验证[8]。
1 理论分析
动摩擦试验的摩擦系数随相对滑动速度的变化可分成4个阶段[6]。第一阶段两物体形成的是弹性变形阶段;第二阶段,两物体接触形成干摩擦状态,此时的摩擦系数在所有阶段中最大,但还存在一定的边界润滑状态;第三阶段,相对滑动速度随时间增加,两物体之间由于高速摩擦发热使材料之间形成微熔或者融化状态,形成局部流体润滑,很显然这样的熔化是很微观的,不易被察觉,此时的滑动摩擦系数将减小,相当于熔融物质在接触面之间形成了润滑作用;随着时间的进行,进入最后一个阶段,此时处在全面润滑状态并且熔融物质被两个面磨蚀掉,动摩擦系数稍微增加。归纳起来:滑动摩擦系数刚开始最大,随着相对滑动速度的增加,动摩擦系数快速下降,下降到一定阶段后随着相对滑动速度的增加动摩擦系数又缓慢增加,滑动摩擦系数随相对滑动速度的变化曲线如图2所示。
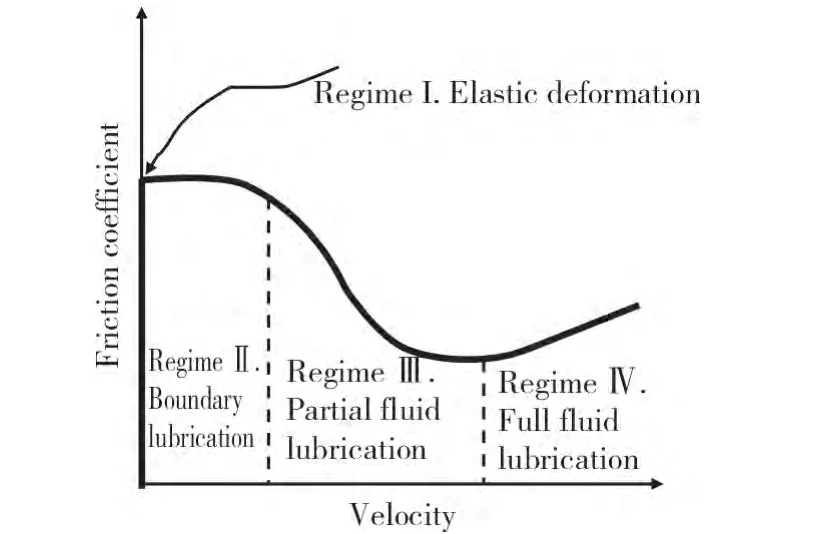
图2 滑动摩擦因数随速度变化图[6]Fig.2 The variation diagam of kinematic friction coefficient versus sliding velocity[6]
由上述滑动摩擦的理论模型可看出,在滑块滑动过程中,材料发生的变形主要是弹性变形,所以在确定试样材料后,仅需其杨氏模量、泊松比和密度。在工程上主要运用钢、铝合金、高聚物、混凝土等常用材料。因此,在有限元验证分析中选择常用材料可很好地验证所设计的动摩擦实验装置是否满足预期目标。材料参数和滑板坡度如表2所示。
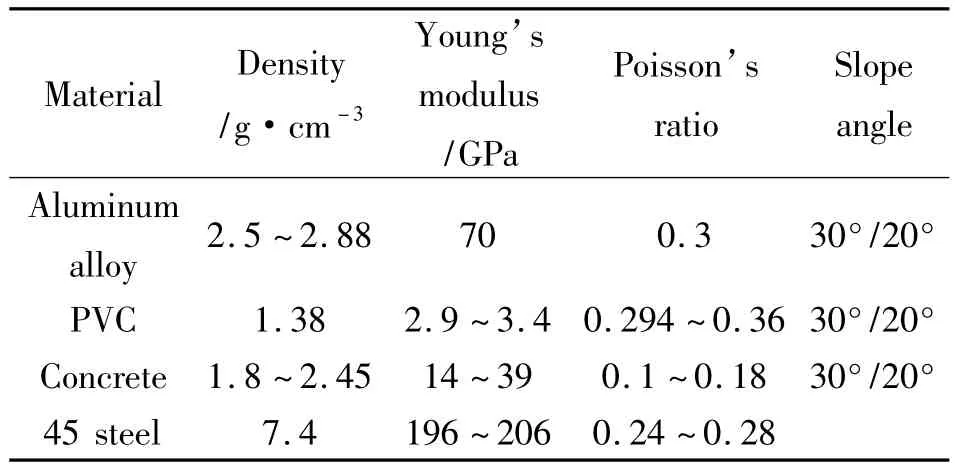
表2 数值模拟中的材料参数[9]Table 2 The material parameters in numerical simulations[9]
2 数值模拟及结果分析
基于有限元商业软件ABAQUS/CAE 6.11-1,采用Dynamic/Explicit模块进行分析,分析时间设置为1 s。滑块与滑板之间定义为surface-to-surface(Explicit)面面接触。将滑板定义为完全固支。在滑块上施加不同的加速度载荷进行分析。
基于所得到的滑块在滑板上的切向加速度数据a(t),根据下式得到动摩擦系数以及相对滑动速度,
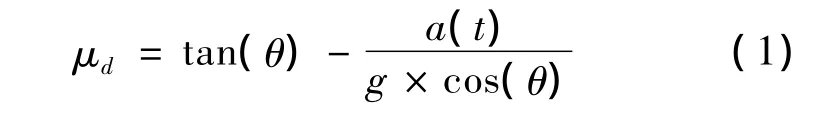
其中θ为滑板与水平面之间的夹角,本次分析中采用的是θ=30°或θ=20°;g为重力加速度。
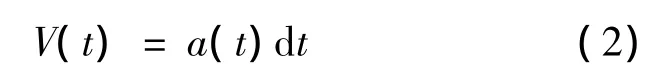
对数据进行处理得到数据图像,纵坐标为相对值,其中μs为静摩擦系数。图3为模拟具有不同材料参数的铝合金在45钢表面滑动所得的动静摩擦系数比值及相对滑动速度关系的数值结果与理论结果的对比。其中理论结果由文献[10]基于图2给出的如下式所示的表达式描述:

其中P1-P4为式(3)中的常数。由图3可知,数值分析得到的数据与理论数据吻合,说明该动摩擦实验装置可用于测量铝合金和45钢表面的滑动摩擦系数。
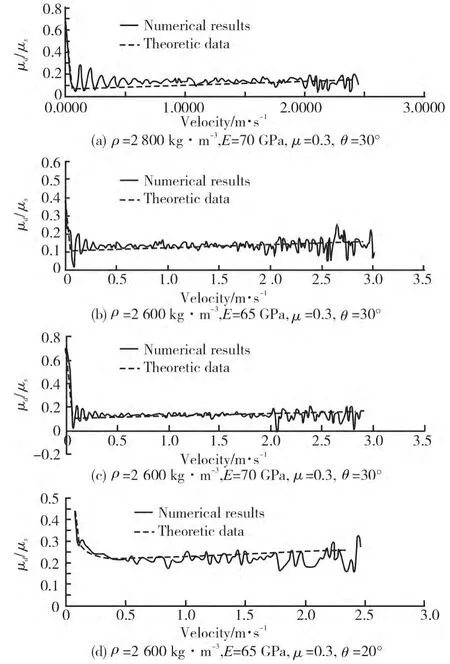
图3 具有不同参数的铝合金材料与45钢之间的滑动摩擦系数Fig.3 The kinematic friction coefficient between 45 steel and aluminum alloy with various material parameters
同样地,图4为具有不同材料属性的混凝土与45钢表面动摩擦实验的有限元分析数据和理论模型的对比。由图可知,混凝土材料与45钢之间的滑动摩擦关系符合滑动摩擦理论模型,证明混凝土材料的滑动摩擦系数的测量可在所设计的装置上进行。
最后,图5为具有不同材料参数的聚氯乙烯(PVC)在45钢表面滑动ABAQUS有限元分析数据和理论模型之间的对比。由图可知,PVC材料在45钢表面滑动的动摩擦系数和理论模型十分吻合,说明所设计的滑动摩擦试验装置能很好地测试PVC为代表的聚合物材料在45钢表面的滑动摩擦系数随相对滑动速度的变化关系。
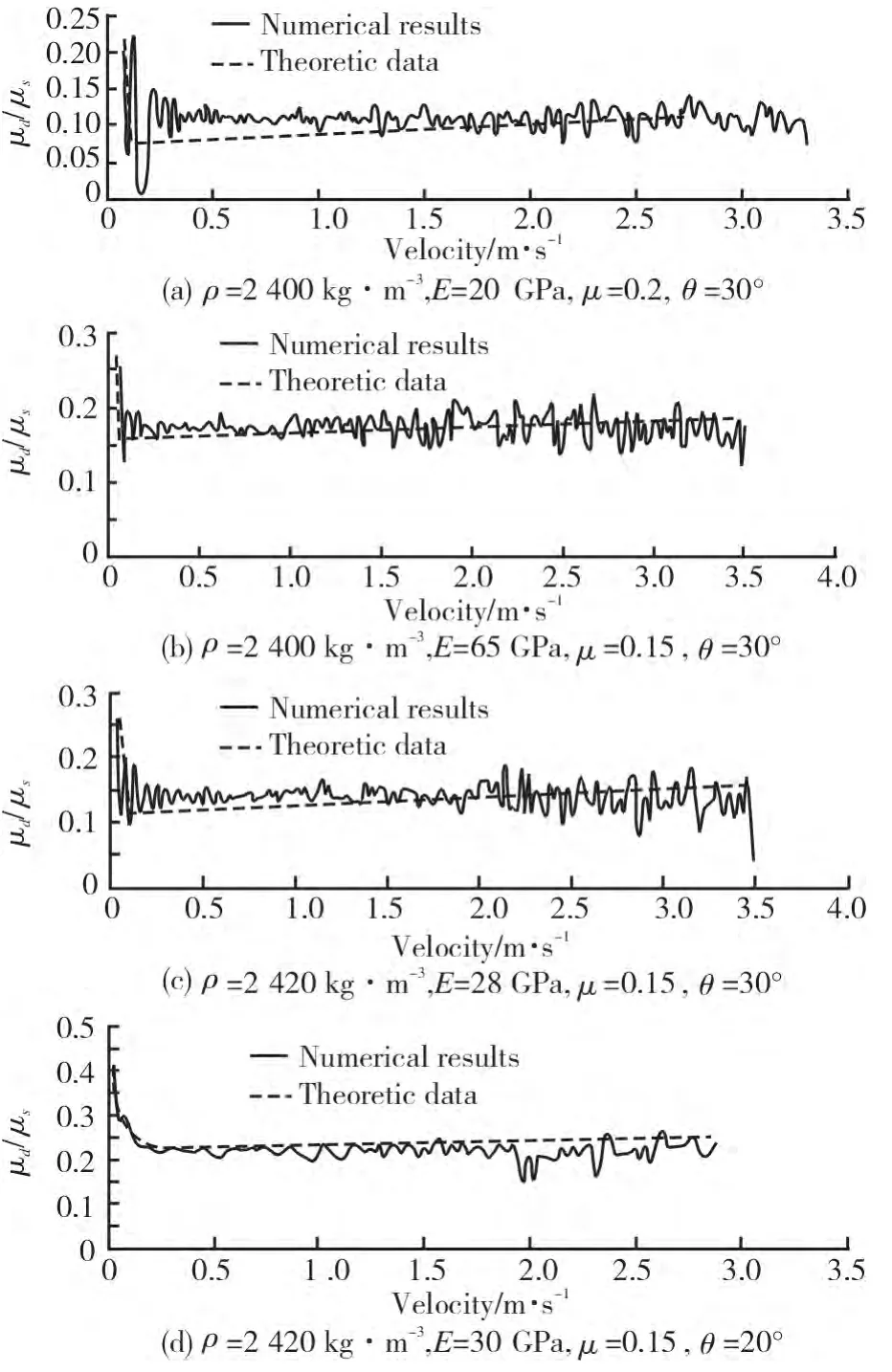
图4 具有不同参数的混凝土材料与45钢之间的滑动摩擦系数Fig.4 The kinematic friction coefficient between 45 steel and concrete with various material parameters
3 结论
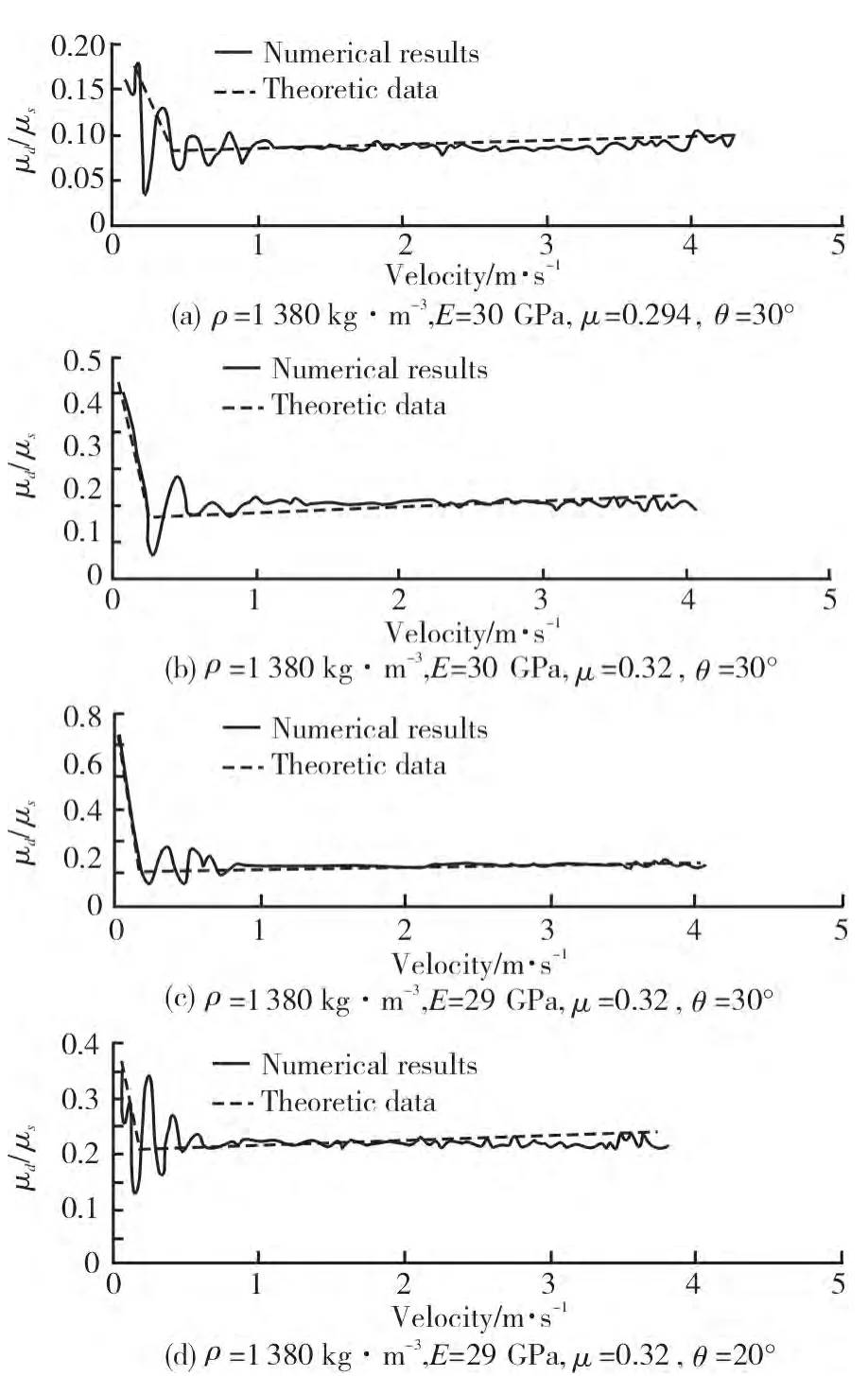
图5 具有不同参数的PVC材料与45钢之间的滑动摩擦系数Fig.5 The kinematic friction coefficient between 45 steel and PVC with various material parameters
以往大多动摩擦试验测试装置所能达到的相对滑动速度仅局限于 2.5 mm/s~2.54 m/s。然而,利用这些装置获得一个较宽范围内的相对滑动速度对动摩擦系数的影响关系却很困难。基于笔者设计的新型动摩擦试验装置,可测量相对滑动速度在10 m/s以内的动摩擦系数。本文通过数值模拟发现常见的3种材料(铝合金、混凝土、PVC)取不同参数条件下在45钢表面的滑动摩擦系数的模拟结果能很好地符合理论模型。说明3种材料所代表的金属材料、地质材料和高聚物材料在45钢表面的滑动摩擦系数随相对滑动速度的变化关系与理论模型吻合,验证了所设计的动摩擦实验装置的可靠性和实用性。
[1]林玉亮,卢芳云,崔云霄.冲击加载条件下材料之间摩擦系数的确定[J].摩擦学学报,2007,27(1):64-67.
[2]王晓燕,卢芳云,林玉亮.SHPB实验中端面摩擦效应的研究[J].爆炸与冲击,2006,26(2):134-139.
[3]钮瑛.利用模型法测定动摩擦因数的几种方法[J].物理教师,2012,33(10):69-72.
[4]李振学.动摩擦系数的一种计算方法[J].武汉化工学院学报,1998,20(3):80-82.
[5]龚中良,黄平.基于非连续能量耗散的滑动摩擦系数计算模型[J].物理学报,2011,2:1-6.
[6]MENG H.Numerical split Hopkinson pressure bar(NSHPB)test and its applications in the assessment and improvement of SHPB test results[D].Singapore:Nanyang Technological University,2003,75-103.
[7]施宝兴.用加速度传感器直接测量加速度的实验验证[J].南京体育学院学报,2001,15(1):4-6.
[8]石亦平,周玉蓉.ABAQUS有限元分析实例讲解[M].北京:机械工业出版社,2006,9-51,125-145.
[9]孙康宁,李爱菊.工程材料及其成形技术基础[M].北京:高等教育出版社,2009.
[10]卢玉斌,宋丹路,李庆明,等.分离式霍普金森压杆试验中工程材料端面摩擦模型的确定[J].振动与冲击,2012,31(3):18-22.

