基于谐波小波包变换的信号检测
侯铁双, 罗祖军, 周 有
(西安邮电大学 自动化学院, 陕西 西安 710121)
基于谐波小波包变换的信号检测
侯铁双, 罗祖军, 周 有
(西安邮电大学 自动化学院, 陕西 西安 710121)
利用二进离散小波变换检测周期性信号时,由于频带间的干扰,微弱成分易被强信号所淹没,为解决此问题,提出一种基于谐波小波包变换的周期性信号检测算法。利用谐波小波函数的盒形频谱结构,根据目标声信号的特点,选择合适的分解层数和分析带宽,由此避免分析频带之间的相互干扰。对实测数据的分析结果表明,谐波小波包变换对于低信噪比下的微弱线谱信号成分有一定的增强效果。
水声信号处理;信号增强;谐波小波包变换
在利用声纳等水声设备探测目标的过程中,目标辐射信号中的稳定线谱对应于目标上的一些周期性振动源,在一定程度上可用于确定目标的航速、类型,进而实现目标的检测与分类。
研究舰船的安静性技术方面一直是各国重点的研究方向并取得很大的成就,使得舰船声辐射能量有大幅度的下降,与此相反由于海上航运、海洋开发等活动的日益频繁,使得海洋环境噪声大幅度增加,这对采用被动技术的目标检测增加了技术难度,为了降低环境噪声对信号检测性能的影响,研究合适的线谱检测算法很有必要[1]。
检测水声目标信号中线谱成分的研究有两种方法:一是通过对调制的信号进行解调,得到低频线谱,这种方法主要用于调制比较明显的情况[2];二是直接对低通滤波后的信号进行变换,得到低频分量,这种方法用于调制信息不明确的情况[3]。这种方法在一定程度上可以检测出目标中的某些线谱成分,但是由于目标中的线谱成分可能分布于不同的频带内,这种分析方法可能会由于频带间干扰的存在使得能量较大的成分完全淹没能量较低的线谱成分。
谐波小波除具有通常意义下的小波变化的特点外,还具有自身的优势:小波函数具有明确的数学表达式,无需通过尺度函数迭代的方法构造;不受二进制限制,算法实现简单[4]。文献[5]通过算例和工程实例,实现了强噪声下微弱周期信号的提取,并证明了谐波小波函数在微弱信号的频域提取能力和精度上明显优于二进小波。随后的一些研究也都证明了谐波小波函数在检测微弱周期性信号中的有效性[6-9]。
本文从谐波小波函数的盒形(Box-like)频谱结构的性质出发,利用谐波小波包变换实现微弱周期性信号增强,并通过实测信号验证谐波小波包检测微弱周期性信号的有效性。
1 谐波小波变换
1.1 谐波小波函数
与通过双尺度方程构造小波函数不同,谐波小波以小波函数的频谱为出发点,构造具有盒形频谱的带通滤波器作为谐波小波函数的频谱,其表达式为[4]
(2)
对式(1)做傅里叶逆变换,就得到了谐波小波函数时域表达式
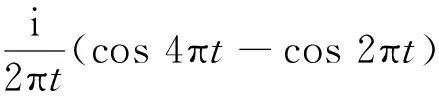
(2)
用变量(2jt-k)替换式(2)中的变量t,这样就得到了谐波小波ψ(t)的二进函数
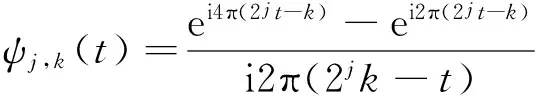
(3)
式中j是尺度参数,也称为小波的分解层,实现对式(2)所表示的ψ(t)压缩2j倍,k是位移参数,表示分析中心位于t=k。
图1所示为不同分解层上谐波小波的傅里叶变换的带宽与幅值关系[4],从中可以看出,随着j的增大,时间分辨率降低,频率分辨率增大。

图1 带宽与幅值的关系
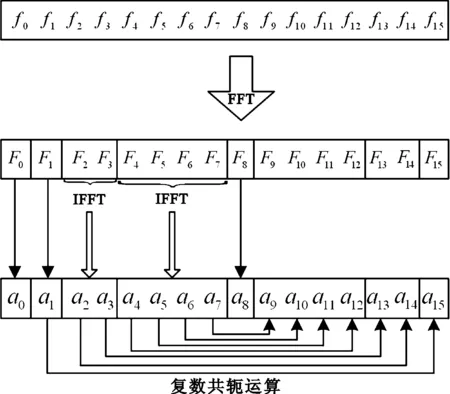
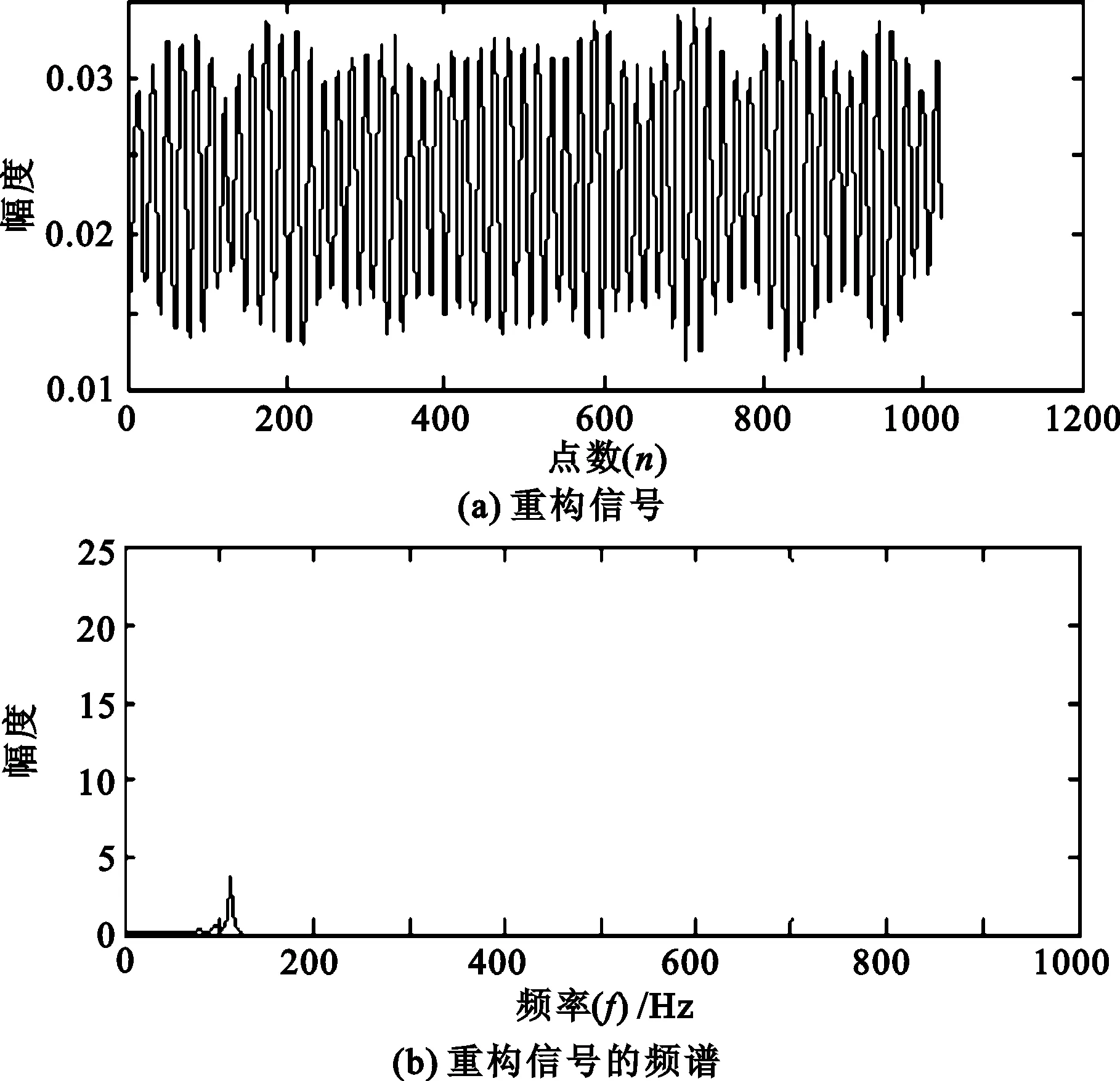
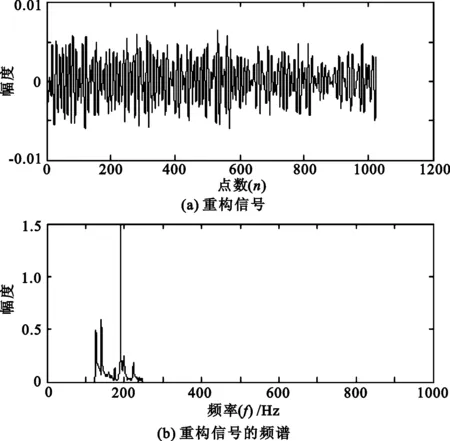
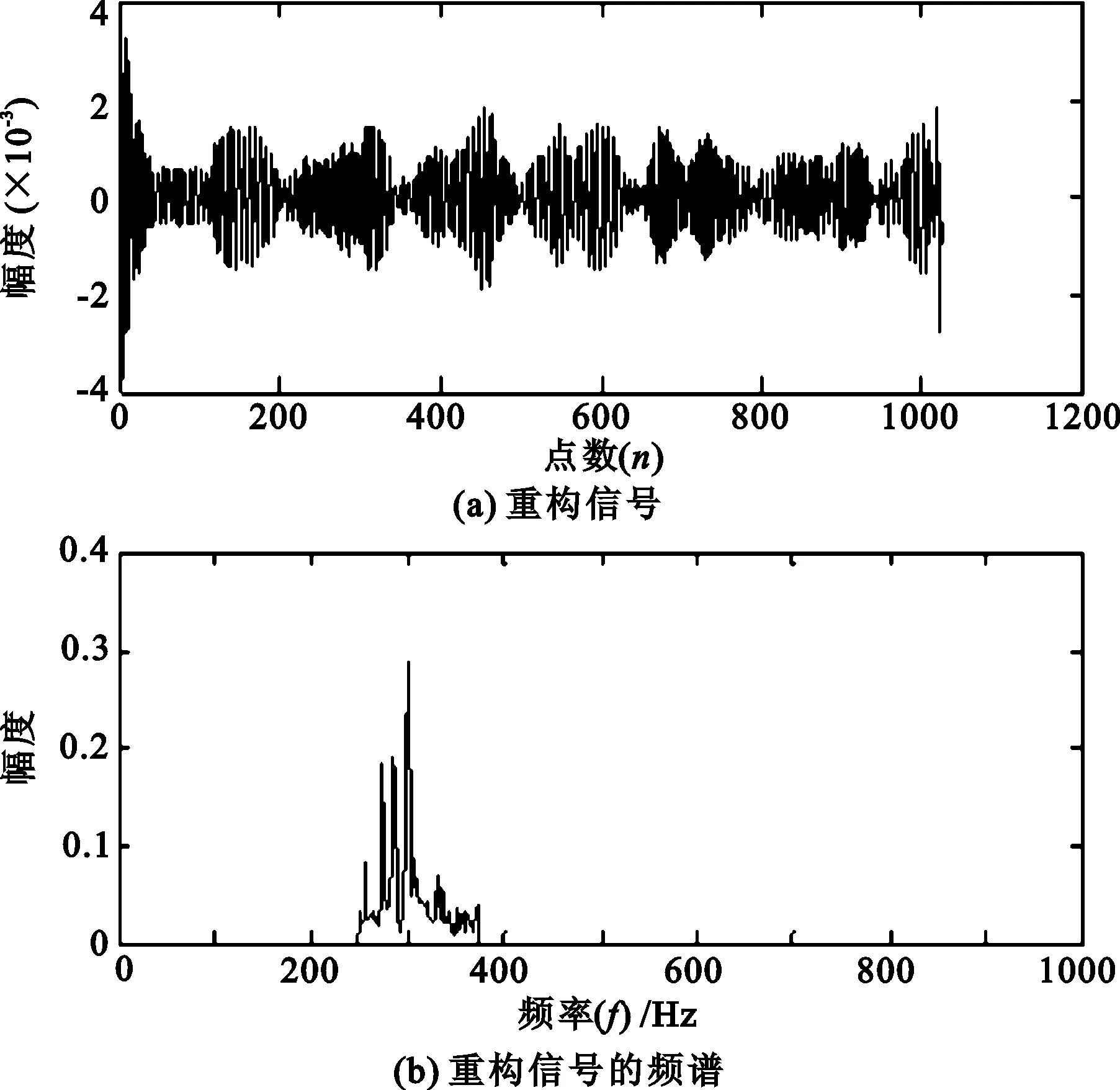
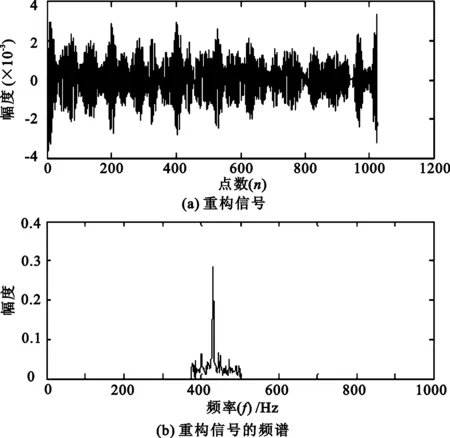
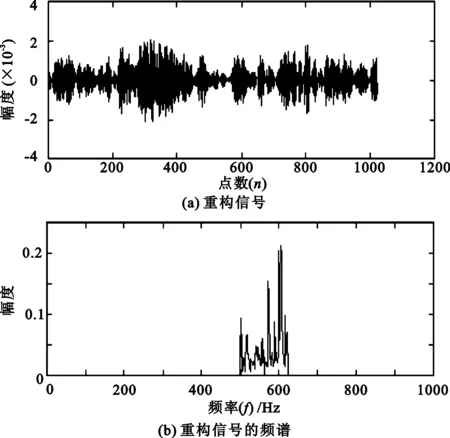
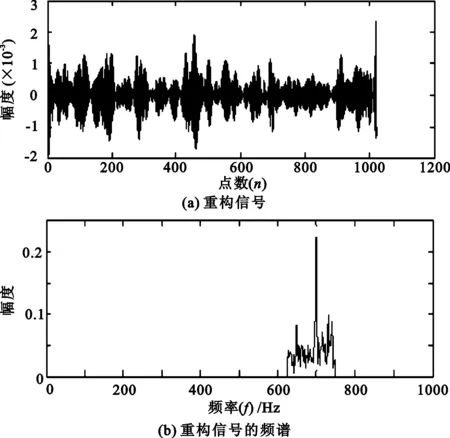
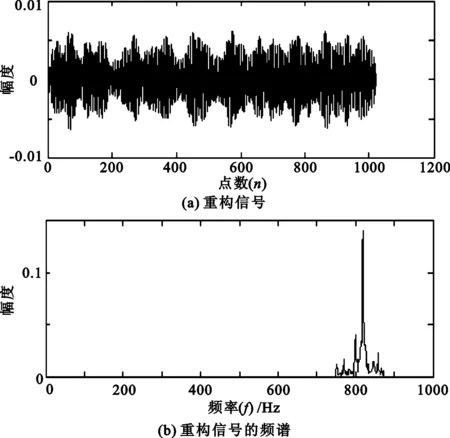
假设要分析的频带范围为[2πm,2πn](m (4) 此时小波函数在时域的表达式为 (5) (6) 分析式(6),可得到谐波小波函数的正交特性。 (1) 不重合的不同频带对应的小波函数相互正交。 (2) 同一频带内,不同非零k值对应的小波函数相互正交。 谐波小波函数的这种正交特性更具有普遍适用性,可以更加灵活地实现对信号的分析。利用谐波小波函数系ψm,n(t)构造成L2()的一组正交基,对信号作谐波小波分解时,可以将信号分解成许多无频段间干扰的独立频段,各频段内微弱的信号由于不受相邻频段的干扰而得以准确显示,这对于微弱信号的检测具有重要意义。 1.2 谐波小波变换快速算法 设有离散信号f(r)(r=0,1,…,N-1),对f(r)进行傅里叶变换得到傅立叶系数 (7) 根据傅里叶变换的性质,有 (8) 并且,N个傅里叶系数中,除F0与FN/2为实数外,其余一般均为复数。 假设相应的小波系数为as(s=0,1,…,N-1),由于小波系数类似于傅里叶系数,因此有 aN-s=as(s=1,2,…,N/2), (9) 并且除a0和aN/2外,其他系数一般为复数。 由图1可以看出,第j层中,2j个小波系数a2j+k(k=0,1,…,2j-1)对应于信号f(r)的傅里叶系数F2j+k(k=0,1,…,2j-1)。j层的第一个小波系数为a2j,具有1/2j的常谱密度,因此它对傅里叶系数Fm(2j≤m≤2j+1)的贡献为a2j/2j。j层的第二个小波系数为a2j+1,与上一个小波相比有1/2j平移,因此它的傅里叶变换也就比上一个小波有e-iωk/2j的偏移量,由于Fm对应于频率ω=2πm,因此a2j+1对Fm的贡献为a2j+1e-i2πm/2j/2j。将k=0,1,…,2j-1的所有贡献组合,得到 (10) 此式即为傅里叶系数与谐波小波系数之间的关系式。用n=2j和s=m-n对式(10)做变量代换,对于s=0,1,…,n-1有 (11) 以16个采样点的实信号为例,得到图2所示的小波系数计算示意图[4]。结合以上分析及图2可知,谐波小波系数可以通过对信号的傅里叶系数进行傅里叶逆变换得到,从而使得谐波小波相对于二进小波具有计算速度上的优势。谐波小波在许多领域都有应用[5-8]。 图2 16序列的实信号的谐波小波算法 基于傅里叶的谐波小波分解为谐波小波变换提供了快速算法,而有些情况下,需要对信号的高频部分得到与低频部分同等的分析效果,此时难以用小波变换处理,而小波包变换正好可以处理这类问题。 设第j层上各小波的分析带宽为 B=fh/2j-1, (12) 待分析频带的上、下限分别为 m=sB,n=(s+1)B (s=0,1,…,2j-1)。 (13) 谐波小波包分解的频域分布如图3所示。随着对信号分解的不断深入,谐波小波包{ψm,n(t)}就实现了信号整个频带的细化,直到达到分解要求为止。由图可以看出,我们可以根据对信号分析的需要选择感兴趣的频段,进而对相应频带进行小波包分解,并利用小波系数对信号进行重构。 图3 谐波小波包分解的频域分布 利用谐波小波包进行信号分析时,根据信号的特点可以很容易地选择合适的分解层数j和分析带宽B。由于没有计算小波包系数Wm,n,k的快速算法,不妨考虑采用循环卷积算法来求解。 为验证谐波小波包检测信号中微弱线谱成分的效果,将谐波小波包变换对海上实验所测得的某舰船的通过特性数据进行分析。对于待分析信号取采样频率fs=2 000 Hz,根据式(12)和式(13)确定信号的分析带宽B以及需要分解的层数j。取分解层数j=4,则分析带宽 图4至图11为对某舰船辐射声信号进行谐波小波包变换下各频带内的重构信号及频谱图。 可以看出,图4中的110 Hz、图5中的191 Hz、图7中的430 Hz、图9中的700 Hz、图10中的820 Hz线谱都很清晰地在各个频段突显出来。 与谐波小波时频图和功率谱图相比较,由于谐波小波包可以将需要分析的频带从整个频带范围内拿出来分析,减少了频带之间的相互干扰,使得各窄带内的分量表示地更清晰,对于淹没在强噪声背景下的微弱信号检测有重要意义。 图4 0~125 Hz频段的分析与重构结果 图5 125~250 Hz频段的分析与重构结果 图6 250~375 Hz频段的分析与重构结果 图7 375~500 Hz频段的分析与重构结果 图8 500~625 Hz频段的分析与重构结果 图9 625~750 Hz频段的分析与重构结果 图10 750~875 Hz频段的分析与重构结果 图11 875~1 000 Hz频段的分析与重构结果。 在介绍谐波小波变换的基础上,提出了水声目标辐射噪声信号的谐波小波包分析方法,并且利用谐波小波包变换检测出了藉助功率谱分析和谐波小波变换下不能检测出的线谱成分。对实验测量所得实测数据的分析表明,谐波小波包变换能够有效增强水声目标噪声中的微弱线谱成分。 [1] 侯铁双.基于小波变换和支持向量机的声引信信号检测研究[D]. 西安: 西北工业大学,2010. [2] 侯铁双.基于解析小波变换的信号包络检测[J].西安邮电学院学报,2011,16(3):18-21. [3] 陈敬军,孟昭文,陆佶人. 模糊专家系统在线谱检测中的应用研究[J].船舶工程,2006,26(6):67-70. [4] Newland D E. Harmonic wavelet analysis[J].Proceedings of the Royal Society A, 1993,443:203-225. [5] 李舜铭,许庆余. 微弱振动信号的谐波小波频域提取[J].西安交通大学学报,2004,38(1):51-55. [6] 娄琳,贾耀增.谐波小波自适应滤波技术研究[J].机械科学与技术,2012,31(9):1486-1489. [7] 李彦彦,华晨辉.谐波小波在旋转机械故障诊断中的应用[J].辽宁工程技术大学学报:自然科学版,2012,31(1):123-126. [8] 王冬云,张建刚,秦红义,等. 应用谐波小波包提取转子故障特征方法[J].哈尔滨工程大学学报,2012,33(7):875-880. [9] 田福庆,罗荣.改进的谐波小波包变换及其在微弱故障特征提取中的应用[J]. 震动与冲击,2013,32(17):29-34. [责任编辑:王辉] Signal detection based on harmonic wavelet packet transform HOU Tieshuang, LUO Zujun, ZHOU You (School of Automation, Xi’an University of Posts and Telecommunications, Xi’an 710121, China) The weak signal can be submerged in the strong signal or ambient noise because of the inter-band interference when the dyadic wavelet is used to detect the line spectrum. To solve this problem, a harmonic wavelet packet transform is proposed to detect the line spectrum. With box-like spectrum of the harmonic wavelet function and according to the nature of the target-radiated noise, the analysed level and bandwidth can be appropriately chosen; therefore the inter-band interference can be reduced. Results show that the harmonic wavelet packet transform can enhance the weak line spectrum components under the low signal-to-noise ratio. underwater signal processing, signal enhancement, harmonic wavelet packet transform 10.13682/j.issn.2095-6533.2014.05.012 2014-03-11 陕西省教育厅专项科研计划基金资助项目(2011JK0937) 侯铁双(1976-),男,博士,讲师,从事信号与信息处理研究。E-mail: htshuang@hotmail.com 罗祖军(1965-),男,博士,副教授,从事现代控制理论研究。E-mail:lzjpool@xupt.edu.cn TN911.7 A 2095-6533(2014)05-0061-05
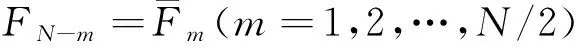
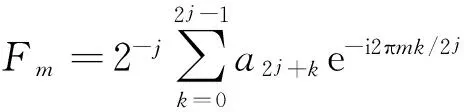
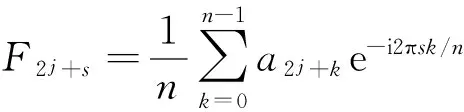
2 谐波小波包变换

3 谐波小波包分析的数据验证
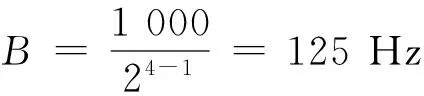

4 结 语

