模糊C-均值聚类图像分割算法的一种改进
李 琳, 范九伦, 赵 凤
(西安邮电大学 通信与信息工程学院, 陕西 西安 710121)
模糊C-均值聚类图像分割算法的一种改进
李 琳, 范九伦, 赵 凤
(西安邮电大学 通信与信息工程学院, 陕西 西安 710121)
针对传统模糊C-均值聚类算法对含噪图像分割时未充分考虑空间信息的问题,提出一种改进的模糊C-均值聚类算法,将图像的局部和非局部两种空间信息引入到模糊C-均值聚类算法的目标函数中,以使两种空间信息在含噪图像分割中发挥互补作用。将改进算法应用于不同含噪图像的分割实验,结果表明图像像素的均方误差均比改进前有所降低。
图像分割;模糊C-均值聚类;局部空间信息;非局部空间信息
图像分割[1]在许多领域都有着广泛的应用,例如医学影像、卫星图像中定位物体、人脸识别、指纹识别、交通控制系统、机器视觉等。现有的图像分割算法[2-3]主要包括基于阈值、基于边缘、基于区域和基于聚类等。在聚类算法中,硬C-均值(HCM)和模糊C-均值(FCM)[4-5]是最常用的聚类算法。与HCM聚类算法相比,FCM聚类算法为图像的每一个像素的归属引入了模糊性,使得FCM聚类算法可以更好的保留原始图像的信息。但是当图像被噪声污染后,FCM聚类算法的鲁棒性差,分割结果很不理想。究其原因在于它未充分考虑相邻像素之间存在的空间相关性。此外,FCM算法没有对样本特征进行优化,只是基于样本特征间的欧式距离进行聚类,所以这种方法依赖于输入样本的分布情况。
针对含噪图像的分割问题,近年来研究者们提出了许多FCM的改进算法。Ahmed等人[6]在FCM中引入了局部空间信息[7],他提出的算法被称为FCM-S。然而该算法在每一次迭代中都必须计算所添加的局部空间信息量,这就大大增加了聚类的时间。为了解决这一问题,陈松灿等人[8]提出了FCM-S1和FCM-S2,这两种算法引入了两种空间限制,一种是局部均值的空间限制,一种是局部中值的空间限制,这两种空间限制都是在聚类之前算出来的,这就节约了聚类的时间。但是,当图像被噪声严重污染时,像素的局部空间信息也可能会被污染。此时,像素的局部空间信息就会失去其在含噪图像分割中的指导作用。需要指出的是,对于每一个像素,图像中存在很多像素与它具有相似的邻域结构,且其对于含噪图像分割的指导作用比邻域空间信息的作用更为有效,将这种信息称为非局部空间信息[9]。鉴于此,赵凤等人[10]将非局部空间信息引入到FCM算法中,提出了一种基于非局部空间信息的模糊C-均值 (FCM-NLS) 聚类算法,与使用局部空间信息模糊C-均值聚类算法相比较,取得了更好的分割效果。
无论是FCM-S1和FCM-S2,还是FCM-NLS,这些改进算法都只是单一的利用了局部空间限制或非局部空间限制。一方面,当图像被噪声严重污染时,像素的邻域信息也可能被污染,此时利用局部邻域信息的FCM-S1和FCM-S2聚类算法的分割结果就会很不理想。另一方面,如果只是单一的利用非局部邻域信息对图像进行分割时,FCM-NLS聚类算法无法较好的保持图像的细节特征,也就无法获得更为满意的分割效果。
本文拟利用局部邻域信息和非局部邻域信息在图像分割方面各自的优点,将这两种邻域信息同时引入到FCM中,对模糊C-均值聚类图像分割算法给出一种改进,即基于局部和非局部邻域信息的FCM(FCM-S-NLS)。
1 基于局部和非局部邻域信息的FCM
对于一幅图像
X={x1,x2,…,xn},
其中xk(k=1,2,…,n)表示图像上第k个像素的灰度值,如果将图像X划分为个C区域,并用
V={v1,v2,…,vc}
表示C个区域的聚类中心,{uik}是隶属度矩阵,uik表示xk属于第i个区域的隶属度。
目标函数定义为
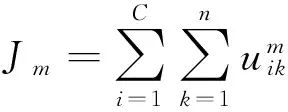
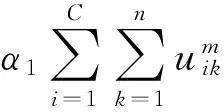
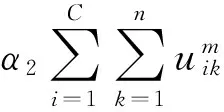
(1)
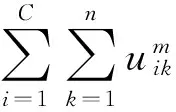
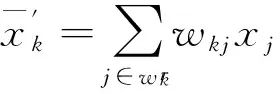
(2)
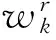
(3)
表示k与j的相似程度,且满足
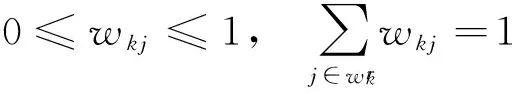

(4)
式(1)的约束条件为

且m为模糊性指数。若记
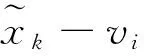
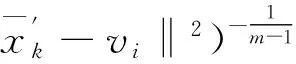
利用拉格朗日乘子法优化该目标函数,可得隶属度矩阵和聚类中心的更新公式
(5)
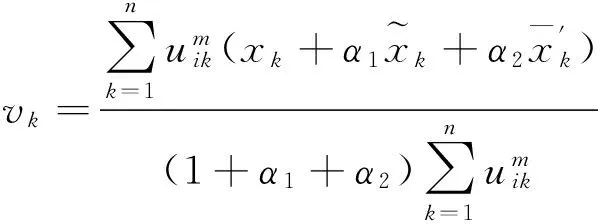
(6)
FCM-S-NLS算法的具体步骤如下,
步骤1 设定一个适当小的数ε<0和最大的迭代次数T。
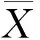
步骤3 初始化聚类中心
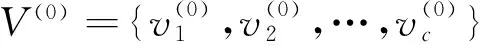
设定迭代参数t=0。
步骤4 利用式(5)更新隶属度矩阵U(t+1)。
步骤5 利用式(6)更新聚类中心V(t+1)。
步骤6 如果‖V(t+1)-V(t)‖<ε或者迭代次数t>T则停止。否则t=t+1返回到步骤4。
2 实验比较与结果分析
为了更好的验证FCM-S-NLS算法的有效性,实验采用了一幅人工合成图像、一幅自然图像和一幅医学图像进行图像分割实验,并对这三幅图像分别添加高斯噪声和椒盐噪声。对于添加高斯噪声的图片,实验中局部空间信息为邻域窗内像素灰度的均值;对于添加椒盐噪声时局部空间信息为邻域窗内像素灰度的中值。
2.1 合成图像的实验结果
2.1.1 合成图像添加椒盐噪声
对合成图像添加椒盐噪声,归一化方差为0.08,图像尺寸为256×256,分类数设置为2,图像所要设置的参数:NR=9(一个3×3的邻域窗),局部邻域信息中,参数取α=3.8,根据基于局部邻域信息的FCM算法[8],只要参数大于3,分割的结果都是比较理想的。对于非局部邻域信息,参数h=30,β=6,此时所得结果都是比较理想的[10]。用新算法(FCM-S-NLS)分割图1(a)时,取α1=3,α2=3, 结果比较理想。

图1 含椒盐噪声人工合成图像分割结果
2.1.2 合成图像添加高斯噪声
高斯噪声的归一化方差为0.8,其余的参数都与上面实验相同。实验结果如图2所示。

图2 含高斯噪声人工合成图像分割结果
2.2 自然图像的分割结果
自然图像添加椒盐噪声或高斯噪声,归一化方差都为0.8,图像尺寸为256×256,分类数设置为2,图像所要设置的参数:NR=9(一个3×3的邻域窗),h=30。在局部邻域信息中,参数α=3.8;在非局部邻域信息中,参数β=6。用FCM-S-NLS算法分割图3(a)和图4(a)时,取α1=3,α2=3.8,结果较理想。
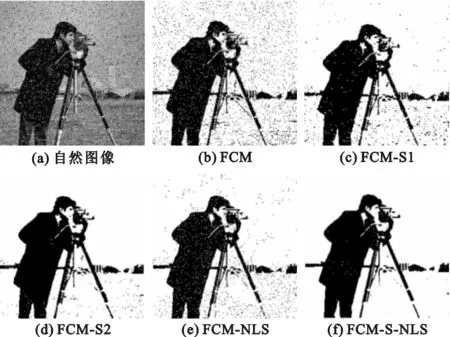
图3 含椒盐噪声自然图像分割结果

图4 含高斯噪声自然图像分割结果
2.3 医学图像的分割结果
对医学图像添加椒盐噪声或高斯噪声,归一化方差为0.008,图像尺寸为303×325,分类数设置为4,图像所要设置的参数:NR=9(一个3×3的邻域窗),h=30。在局部邻域信息中,参数α=3.8;在非局部邻域信息中,参数β=6。用FCM-S-NLS算法分割图5(a)和图6(a),取α1=3.8,α2=3,结果比较理想。
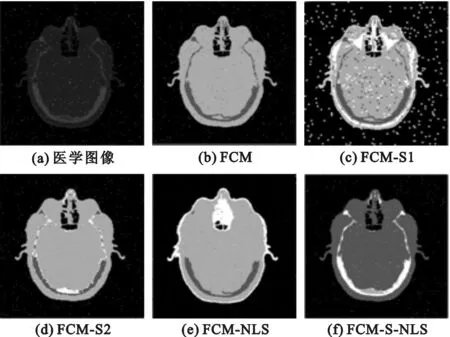
图5 含椒盐噪声医学图像分割结果
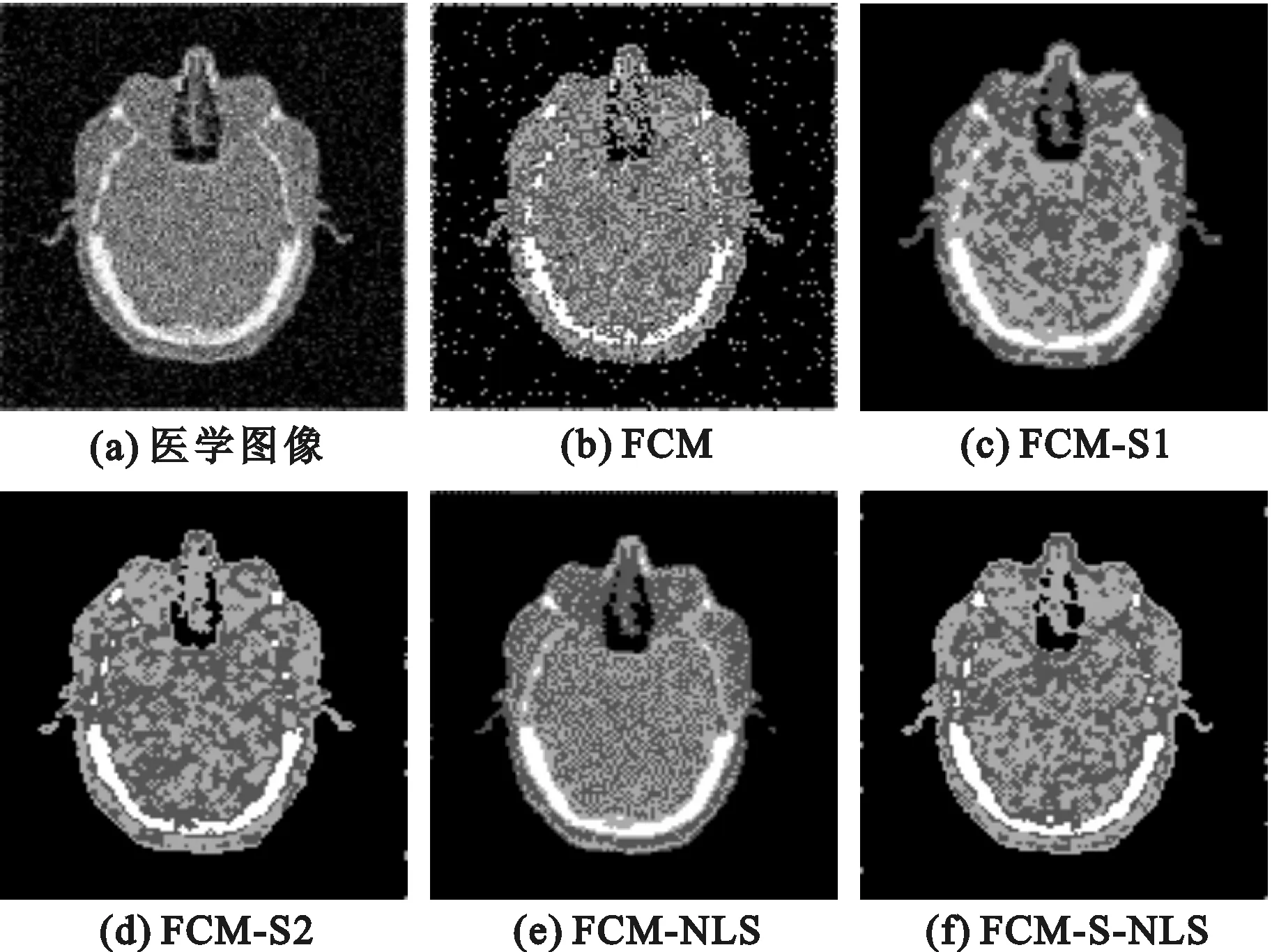
图6 含高斯噪声医学图像分割结果
实验结果展示了不同算法对3种图像的分割结果。从分割结果来看,FCM-S-NLS算法在整体分割效果和对噪声的鲁棒性上是5种算法中最优的,且能保留更多的图像细节息。
2.4 图像分割效果的客观质量评价
为了更好的比较图像分割算法的性能,需要对分割的效果进行客观的质量评价。上面的三组实验仅仅只能通过人的主观判断来评价图像分割的效果,这虽然是最朴素最直接的方法,但是由于人的视觉差异会导致对图像分割性能评价的不统一,故考虑通过图像统计误差中的均方误差(Mean Squared Error, MSE)[11]来实现对图像质量的评价。
令I1和I2分别表示理想图像和分割后的图像,则它们的均方误差公式可表示为

(7)
其中M和N分别表示图像维数的行数和列数。MSE的值EMS越小,则说明两幅图像的相似度越高,即分割效果越理想。
对图像分别添加椒盐噪声、高斯噪声或混合噪声,归一化方差都为0.08,分别用5种方法进行分割(用FCM-S-NLS算法对混合噪声进行分割时,采用局部均值空间限制),分割的结果与理想图像图7(d)比较。表1为像素点的均方误差。图像尺寸为256×256,分类数设置为2,图像所要设置的参数:NR=9(一个3×3的邻域窗),h=30。在局部邻域信息中,参数α=3.8;在非局部邻域信息中,参数β=6。在算法FCM-S-NLS中取参数α1=3,α2=3。

图7 含噪图像及理想分割
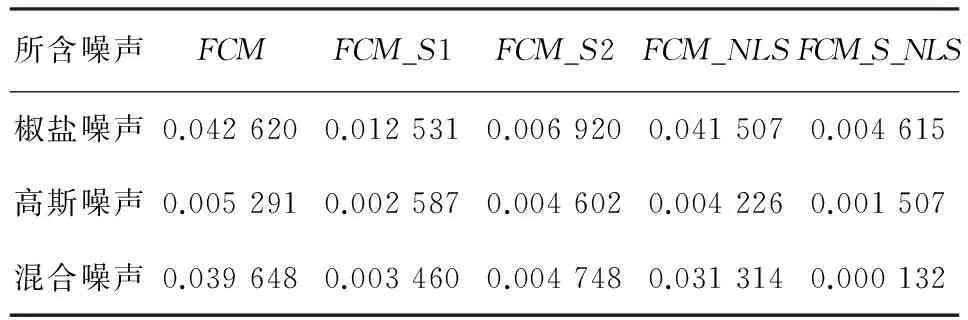
所含噪声FCMFCM_S1FCM_S2FCM_NLSFCM_S_NLS椒盐噪声0.0426200.0125310.0069200.0415070.004615高斯噪声0.0052910.0025870.0046020.0042260.001507混合噪声0.0396480.0034600.0047480.0313140.000132
3 结 语
给出模糊C-均值聚类图像分割算法的一种改进,利用图像的局部和非局部空间信息,可在一定程度上克服常见噪声对图像的影响。仿真实验表明所给FCM-S-NLS算法比已有算法对含噪图像具有更为理想的分割结果。需要指出的是,FCM-S-NLS算法获得局部空间信息和非局部空间信息需要人为的设置一些参数,而这些参数对分割的效果影响也很大,所以如何自适应的确定这些参数是下一步需要研究的内容。
[1] 章毓晋.图像分割[M].北京:科学出版社,2001:2-3.
[2] 李弼程,彭天强,彭波,等.智能图像处理技术[M].北京:电子工业出版社,2004:177-199.
[3] 何俊,葛红,王玉峰.图像分割算法研究综述[J].计算机工程与科学,2009,31(12):58-61.
[4] 李旭超,刘海宽,王飞,白春艳.图像分割中的模糊聚类方法[J].中国图象图形学报,2012,17(4):447-458.
[5] 范九伦.抑制式模糊C-均值聚类研究综述[J].西安邮电大学学报,2014,19(3):1-5.
[6] Ahmed M N, Yamany S M, Mohamed N, et al. A modified fuzzyc-means algorithm for bias field estimation and segmentation of MRI data[J]. IEEE Transactions on Medical Imaging, 2002, 21(3):193-199.
[7] Krinidis S, Chatzis V. A robust fuzzy local informationc-means clustering algorithm[J]. IEEE Transactions on Image Processing, 2010,19(5):1328-1337.
[8] Chen Songcan, Zhang Daoqiang. Robust image segmentation using FCM with spatial constraints based on new kernel-induce distance measure[J]. IEEE Transactions on System, Man and Cybernetics. Part B:Cybernetics, 2004, 34(4): 1907 -1916.
[9] Minh N D, Martin V. Wavelet-based texture retrieval using generalized Gaussian density and Kullback-Leibler distance[J]. IEEE Transactions on Image Processing, 2002,11(2):146-158.
[10] Zhao Feng, Jiao Licheng, Liu Hanqiang. Fuzzyc-means clustering with non local spatial information for noisy image segmentation[J]. Frontiers of Computer Science in China, 2011, 5(1): 45-56.
[11] 任应军,范九伦.一种DWT与背景重构相结合的运动目标分割方法[J].计算机科学,2012,39(10):290-293.
[责任编辑:王辉]
Improvement of fuzzyC-means clustering image segmentation algorithm
LI Lin, FAN Jiulu, ZHAO Feng
(School of Communication and Information Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)
In view of the problem that traditional fuzzyc-means (FCM) clustering segmentation algorithm does not consider the spatial information of noisy image sufficiently, an improved fuzzyc-means (FCM) clustering segmentation algorithm is proposed in this paper. The improved algorithm introduces both local and non-local spatial information into the objective function, and the two spatial information can then play a positive and complementary role in guiding noisy image segmentation.The improved algorithm cab be successfully used for different noisy image segmentation, and segmentation results show that the mean squared error of image pixels are greatly reduced.
image segmentation, fuzzyC-means clustering, local spatial information, non-local spatial information
10.13682/j.issn.2095-6533.2014.05.011
2014-03-12
国家自然科学基金资助项目(61102095,61340040);陕西省自然科学基础研究基金资助项目(2012JQ8045)
李琳(1989-),女,硕士研究生,研究方向为信息安全。E-mail: lin880125@163.com 范九伦(1964-),男,教授,博导,从事模式识别及信息安全研究。E-mail: jiulunf@163.com
TP 391
A
2095-6533(2014)05-0056-05

