不确定微机电混沌系统的反演自适应控制

肖 勇，戴跃洪，张 睿，陈 易

(电子科技大学 机械电子工程学院，成都 611731)

不确定微机电混沌系统的反演自适应控制

肖 勇，戴跃洪，张 睿，陈 易

(电子科技大学 机械电子工程学院，成都 611731)

简单分析了静电力驱动微机电谐振器的混沌特性，给出了系统位移随电压变化的分岔图及典型的混沌吸引子。针对含有不确定的微机电混沌系统，结合反演与自适应控制技术，提出了一种自适应反演混沌控制策略。该策略通过自适应方法在线估计系统中的不确定性，并通过反演控制来快速实现系统的镇定。最后，通过仿真实例验证了所提出的策略的有效性。

微机电系统；混沌；自适应反演控制；不确定性

0 引言

微机电系统是由弹簧、电阻、电容、电感及阻尼器等非线性元器件构成，是一种复杂的非线性系统[1-3]。已经有许多有关学者进行了有关微机电系统的非线性动态行为研究，诸如微机电系统频域响应曲线的弯曲度及跃变现象等[4]。混沌是非线性系统的一种特殊现象，它同样存在于微机电系统中[5]。文献[6]通过建模的方法来预测微机电系统中的混沌行为。文献[7]分析了响应共振条件下接近特定谐振分界线的微机电谐振系统的混沌运动。文献[9]通过Mathieu方程来对微机电振荡器进行建模，并对其非线性混沌特性进行了数字仿真与实验研究。文献[10]发现在开环和闭环的微机电悬臂梁系统中同样存在混沌现象。混沌现象表现为对初始条件的敏感性和不可预测性，在许多实际场合是有害的，必须得到抑制。文献[8]已成功将最优反馈控制控制策略应用于微机电谐振混沌系统，将其快速镇定到期望的周期轨道。文献[11]结合滑模控制与模糊控制，提出了一种存在不确定性的微机电系统谐振系统模糊滑模控制策略，该策略利用模糊方法在线估计系统的不确定性，并进行实时反馈补偿。文献[12]将模糊控制与快速终端滑模控制相结合，利用快速终端滑模控制进一步改善上文的相应能力。文献[13]成功将模糊控制与自适应控制相结合，实现了微机电谐振混沌系统的模糊自适应镇定控制。由于模糊控制结构复杂，且模糊规则的选择对人类的经验具有较强的依赖性，因此，该方法在实际的物理系统应用中有一定的难度。

针对含有不确定性的微机电谐振系统，综合自适应控制和反演控制的优点，提出一种微机电谐振混沌系统的自适应反演控制方法。该方法利用自适应控制来实现系统不确定性的在线估计，并通过反演控制来实现系统的快速镇定。

1 系统描述

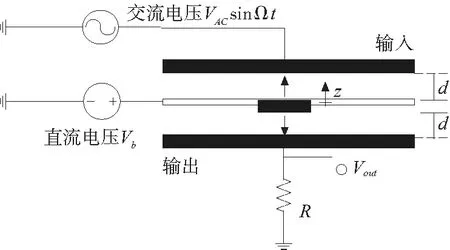
图1 静电力驱动微机械谐振器示意图

图1是静电力驱动微机电系统的结构图。图中，d代表的是微梁间距的初始宽度，z是横梁的垂直偏移量。作用在谐振器上的交流驱动电压和电极与谐振器之间直流偏置电压一起产生静电力驱动力。Vi=Vb+VAC·sinΩτ，其中Vb是直流偏置电压，VAC和Ω分别是交流电压幅值和频率。

假设交流驱动电压的幅值比偏置电压小很多，根据动力学平衡方程，微机电系统的数学模型可以表示为如下的无量纲运动方程：

(1)

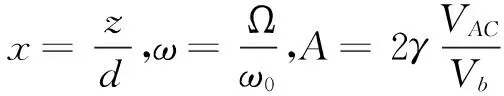
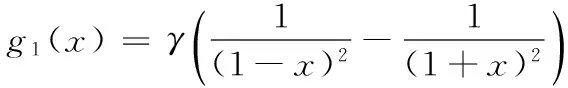
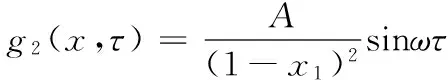
系统(1)可表示为：

(2)

上述无量纲的MEMS谐振系统模型(2)是一个多变量的非线性系统，在一些特定的参数和工作条件下会出现复杂的混沌运动。例如，取α=1,β=12,γ=0.338,μ=0.01,Vb=3.8,ω=0.5，初始状态为(x10,x20)=(0.01,0.1)，以交流电压幅值VAC作为分岔参数[14]可作出MEMS谐振系统的二维相图(图2)和分岔图(图3)所示。从图2可以看出，当VAC=0.1时，系统做周期运动；当VAC=0.15时，系统做准周期运动；当VAC=0.2时，系统做混沌运动。图3是以VAC作为分岔参数，x1和x2作为分岔参数作出的分岔图。

图2 MEMS谐振器的相图

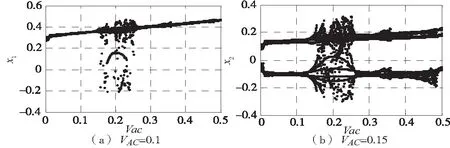
图3 MEMS谐振器的分叉图

2 反演自适应混沌控制

考虑具有如下形式的MEMS混沌系统：

(3)

式中：u是控制输入，δf=Δf(x1,x2)，Δf(x1,x2)为一与系统状态x1和x2有关的不确定项，它表示系统中未建模动态或结构的不确定性。一般假设此不确定项满足条件：|Δf(y)|≤δ，δ为不确定上界，是一个正常数。

假设期望的轨迹为xr，下面设计反演自适应混沌控制器，快速将状态x1镇定到期望轨迹xr，具体设计步骤如下：

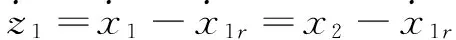
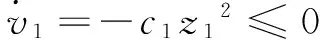
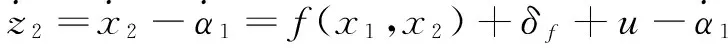
又δf为不可确定的，故取：

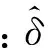
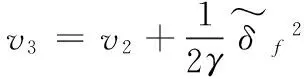
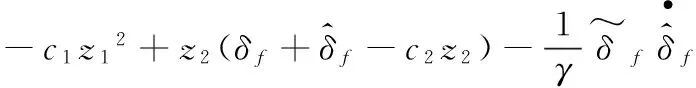
则v3=-c1z12-c2z22≤0。根据Lyapunov稳定理论可知，所设计的控制器是渐进稳定的。

3 仿真结果

为了验证本文所提出的反演自适应控制策略的有效性，对上述微机电谐振混沌系统进行仿真。仿真中采用四阶Runge-Kutta法，采样时间Ts=0.01s，初始条件(x10,x20)=(0.01,0.1)，其参数同第二部分，不再累述。本文的目的是控制状态位置使x其能够跟踪期望轨迹xr=0.2sin(0.5τ)。假定不确定元素Δf(x1,x2)=-0.05sin(x1)受条件|Δf(y1,y2)|≤ρ=0.05所约束。

控制器参数选择如下：c1=10,c2=2,γ=5。控制输入u在τ=200时起作用，图4给出了受控MEMS谐振混沌系统的状态响应及控制输入曲线。

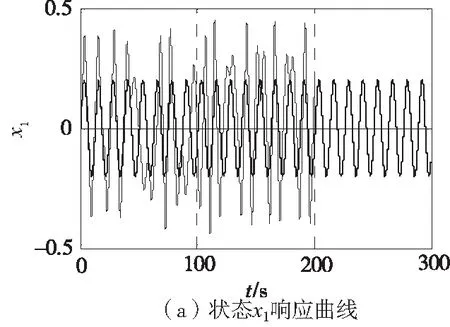
图4 控制作用前后MEMS谐振系统的 状态响应及控制输入曲线

从图4可以看出，未加入控制作用时，系处于混沌状态，在τ=200时加入控制作用，系统能快速的跟踪输入信号。即使系统中存在不确定性，所提出的控制策略仍能有效实现输入信号的跟踪。

4 总结

静电力驱动微谐振系统是一种复杂的非线性系统。本文首先对该系统的混沌特性进行了简单的分析与仿真，其次，针对含有不确定性的MEMS谐振混沌系统，提出了一种反演自适应控制策略。该方法不但结构简单，相应速度快，而且对系统的不确定性具有很强的鲁棒性，能够较好的满足系统性能的要求。最后，通过仿真实例验证了所提出的控制策略的有效性，具有一定的实际应用价值。

[1] M. Roukes. Nanoeletromechanical systems face the future[J]. Phys. World, 2001,14:25.

[2] H. Xie, G.Fedder. Vertical comb-finger capacitive actuation and sensing for coms-MEMS[J]. Sensors Actuators, 2002,95: 212-221.

[3] M.I. Younis, A.H. Nayfeh. A study of the nonlinear response of a resonant microbeam to an electric actuation[J].Nonlinear Dynam., 2003,31:91-117.

[4] R.M.C. Mestrom, R.H.B. Fey, J.T.M. van Beek, K.L. Phan, H. Nijmeijer. Modeling the dynamics of a MEMS resonator: simulations and experiments[J]. Sensors Actuators, 2007,142: 306-315.

[5] Y.C. Wang, S.G. Adams, J.S. Thorp, N.C. MacDonald, P. Hartwell, F. Bertsch. Chaos in MEMS,parameter estimation and its potential application[J]. IEEE Trans. Circuits Syst., 1998,145:1013-1020.

[6] S.K. De, N.R. Aluru. Complex nonlinear oscillations in electrostatically actuated microstructures[J].Microelectromech. Syst., 2005,15:355-369.

[7] A. Luo, F.Y. Wang. Chaotic motion in a micro-electro-mechanical system with non-linearity from capacitors[J]. Commun. Nonlinear Sci. Numer. Simul., 2002,7:31-49.

[8] F.R. Chavarette, J.M. Balthazar, J.L.P. Felix, M. Rafikov. A reducing of a chaotic movement to a periodic orbit of a micro-electro-mechanical system by using an optimal linear control design[J]. Commun. Nonlinear Sci. Numer. Simul., 2009,14: 1844-1853.

[9] E.Barry, M. De, E. Butterfield, J.Moehlis, K. Turner, Chaos for a microelectromechanical oscillator governed by the nonlinear Mathieu equation[J]. J.Microelectromech. Syst., 2007, 16:1314-1323.

[10] S. Liu, A. Davidson, Q. Lin. Simulation studies on nonlinear dynamics and chaos in a MEMS cantilever control system[J]. J.Micromech. Microeng., 2004,14:1064-1073.

[11] H.T. Yau, C.L. Kuo, J.J. Yan. Fuzzy sliding mode control for a class of chaos synchronization with uncertainties[J]. Int.J.Nonlinear Sci. Numer. Simul., 2006,7(2):333-338.

[12] C.L. Kuo. Design of an adaptive fuzzy sliding-mode controller for chaos synchronization[J]. Int.J.Nonlinear Sci. Numer. Simul., 2007,8(4):631-636.

[13] H.X. Li, Z.H. Miao, E.S. Lee. Variable universe stable adaptive fuzzy control of a nonlinear system[J]. Comput. Math. Appl., 2002,44(5-6):799-815.

[14] H.H. Haghighi, A.H.D. Markazi. Chaos prediction and control in MEMS resonators[J]. Commun. Nonlinear Sci. Numer. Simul., 2010,15(10):3091-3099.

[15] V.I. Utkin. Sliding Modes in Control Optimization[M]. Berlin: Springer-Verlag, 1992.

(编辑 李秀敏)

申请优先审稿须知

为振兴我国机械装备制造业，弘扬民族科学文化精神，提升期刊质量，本刊从即日起，凡是符合本刊报道范围且同时受到“国家863计划资助项目”、“国家自然科学基金资助项目”、“国家重点科技攻关资助项目”等国家级基金资助项目的原创论文，可申请优先审稿，一经录用，优先发表，欢迎业内人事、专家、学者踊跃投稿(来稿注明：“优先审稿”字样)。

注：1.本刊正常审稿时间一般为一个月，优先审稿时间为15-20天; 2.本刊正常发表文章周期为来稿后6-8个月，优先发表文章周期为5-6个月。

——本刊编辑部

Back-stepping Adaptive Control of Uncertain Micro-electro-mechanical Chaos System

XIAO Yong，DAI Yue-hong，ZHANG Rui，CHEN Yi

(School of Mechatronics Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China)

The paper analyzes the chaotic behavior of the electrostatically actuated micro-electro-mechanical resonators. The bifurcation diagram about system displacement change with voltage and the typical chaotic attractor are given. Combined with adaptive control and back-stepping approach, an adaptive back-stepping control scheme is proposed for micro-electro-mechanical systems (MEMS) with uncertainties. The uncertainties of the system is estimated using adaptive approach, then back-stepping control is used to stabilize the system as quickly as possible. Finally, simulation results verify that the proposed method is effective.

micro-electro-mechanical systems; chaos; adaptive back-stepping control; uncertainty

1001-2265(2014)07-0106-03

10.13462/j.cnki.mmtamt.2014.07.030

2013-11-04;

2013-12-10

肖勇(1987—)，男，湖北襄阳人，电子科技大学硕士研究生，研究方向机械制造及其自动化，(E-mail)493290092@qq.com。

TH166;TG69

A