缆索吊装系统主索的受力与变形计算

陈俊松，刘飞



缆索吊装系统主索的受力与变形计算

陈俊松，刘飞

（无锡城市职业技术学院 建筑工程系，江苏 无锡 214153）

针对目前悬索理论复杂、不便于施工技术人员掌握的特点，本文提出了一种计算缆索吊装结构受力和变形的简易方法，并应用该方法进行了案例分析，准确计算出主索系统的拉力、挠度和安全系数，验证了该方法的有效性. 本文提出的简易计算方法有助于施工单位设计缆索吊装系统，还可用作施工现场控制的依据，提高施工的安全性.

缆索吊装系统；主索；受力；变形

缆索吊装是常见的吊装系统，主要用在深谷、急流等地势险恶，不便于采用其他吊装方法的场地[1,2]. 近年来，这种施工方法除应用于传统的桥梁施工，也用于一些大型建筑物的施工. 缆索吊装系统由主索、起重索、牵引索、塔架和锚固系统构成，其中主索的受力和变形分析是整个缆索吊装系统的关键[3,4].

目前，对于主索的受力和变形计算一般采用基于悬索桥理论的解析法和有限元法[5-7]. 这两类方法的计算精度高，但比较复杂，不便于一线施工技术人员掌握，这也在一定程度上限制了此类施工方法的大规模应用. 本文基于悬索线型基本理论，采用静力平衡的方法提出一种简易的缆索吊装主索受力与变形的计算方法，以期为缆索吊装系统的设计和施工提供理论依据.

1 理论推导

首先忽略索的弹性变形，假设索型为抛物线型，按静力平衡方程，针对有荷载和无荷载两种情况，分别考虑索的受力和变形. 然后采用修正计算结果的方法来考虑索的弹性变形情况.

1.1 无载荷计算

1.1.1 单跨情况

假设悬索的自重沿水平轴均匀分布，并满足抛物线方程，见图1，则：

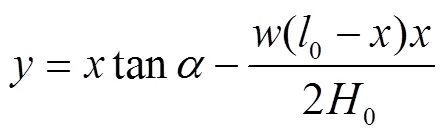
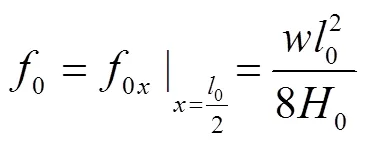
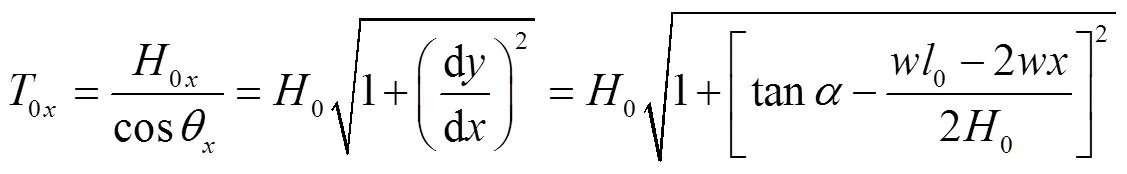
1.1.2 双跨情况

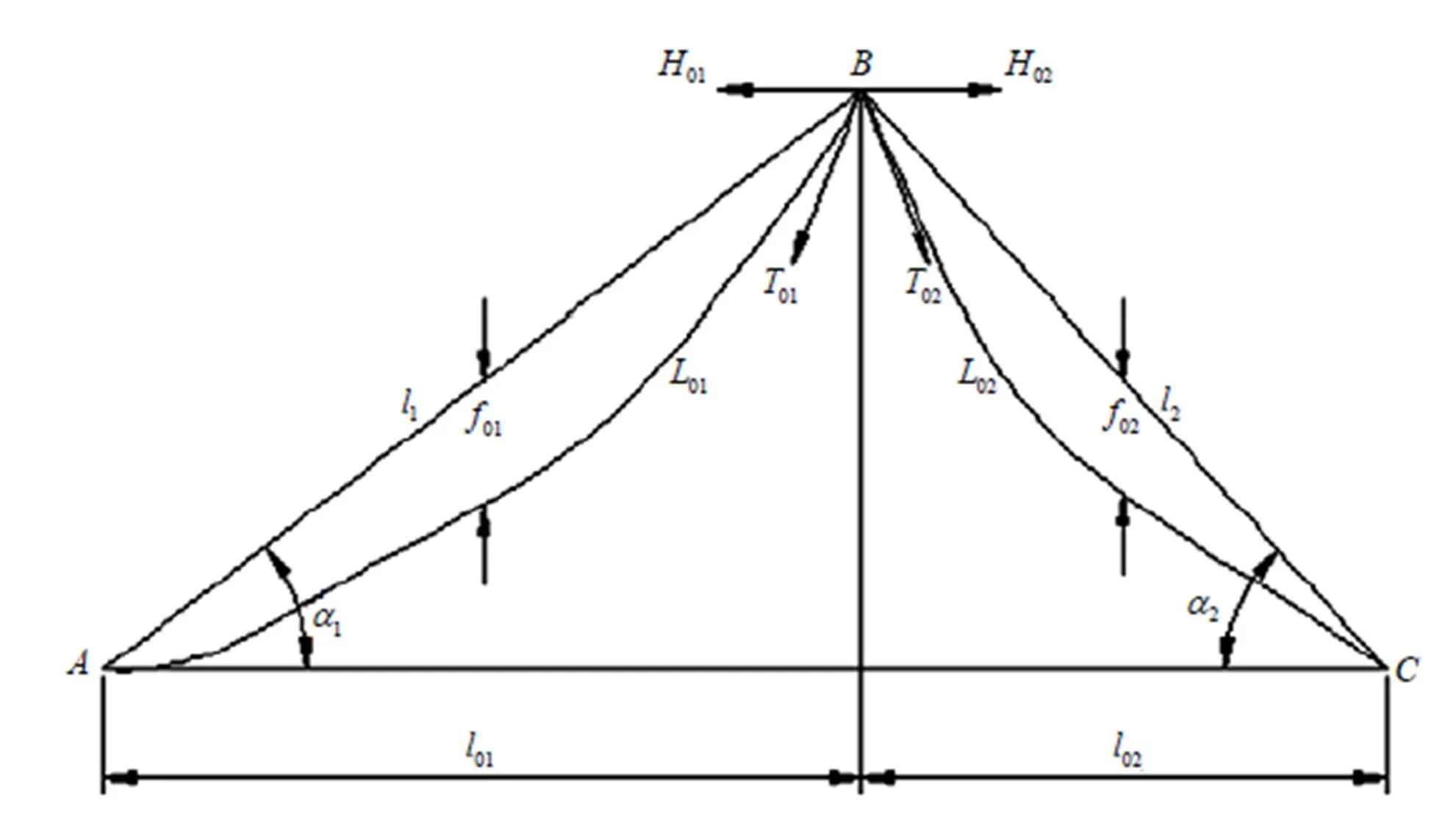
图2 双跨无荷条件下索的受力示意图

由公式（4），可得：

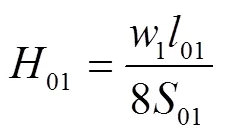
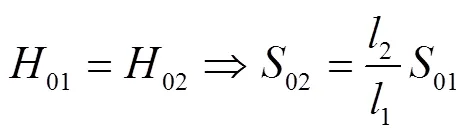
1.2 有荷载计算

1.2.1 单跨情况

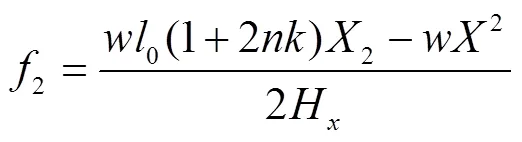
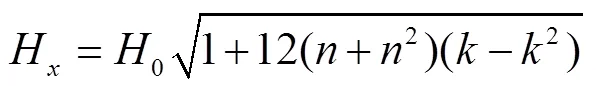
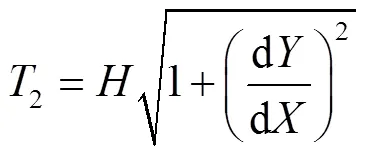
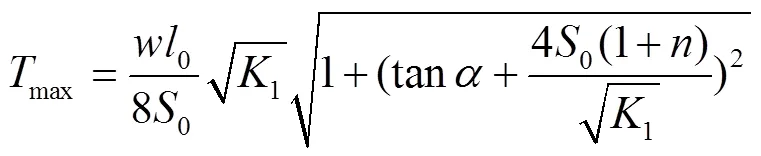
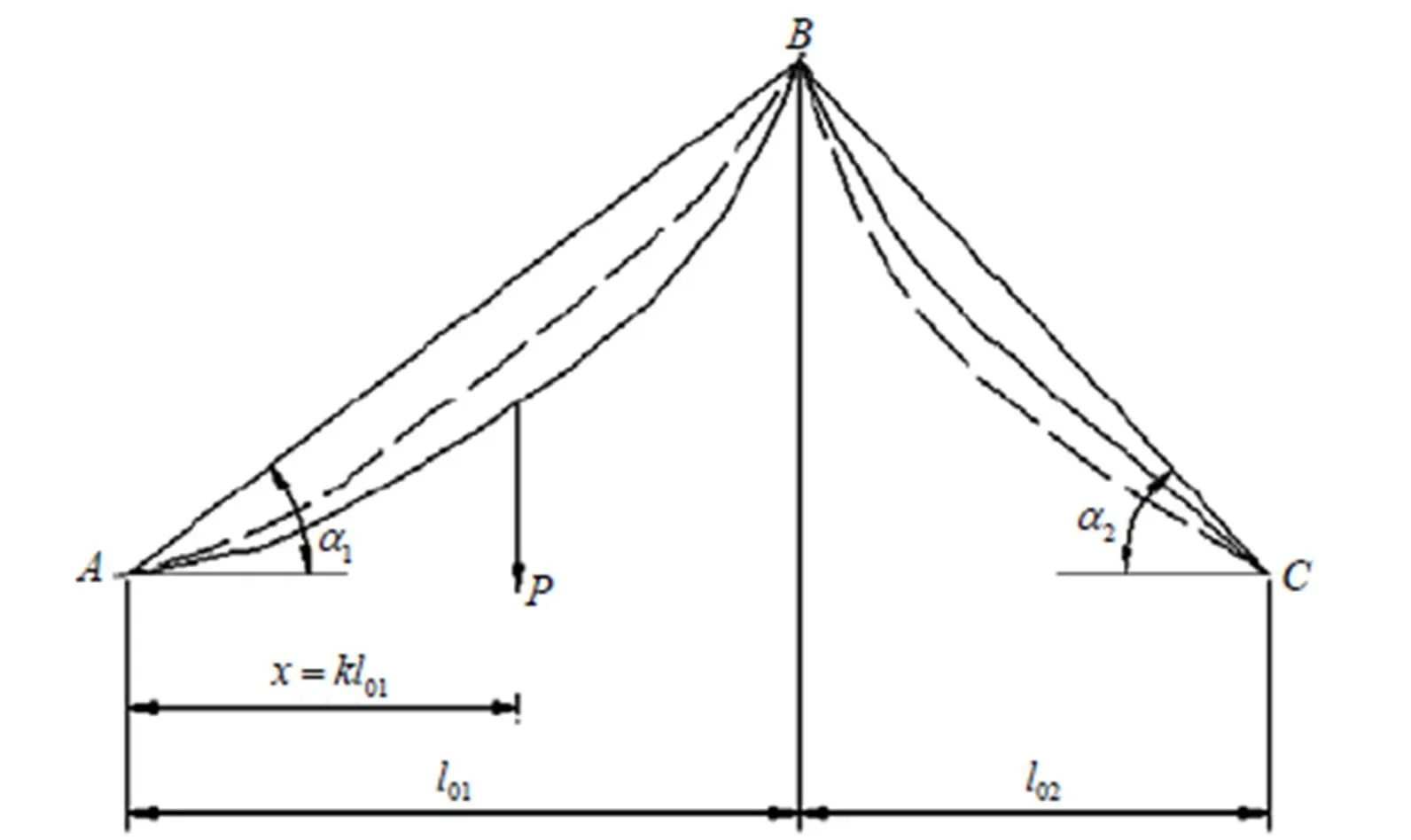
图4 双跨集中荷载条件下索的受力示意图

1.2.2 双跨情况

受力示意图如图4所示，由公式（4）可得两跨的无荷悬索长度为：

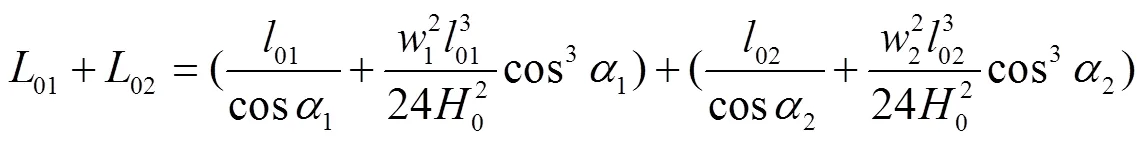
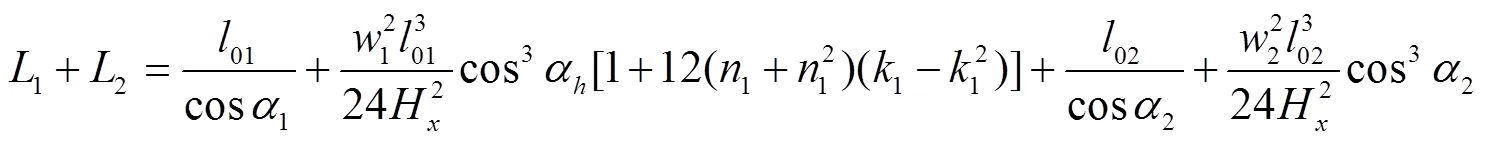
设悬索受荷前后其长度不变，则：

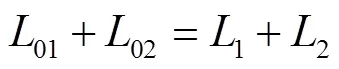
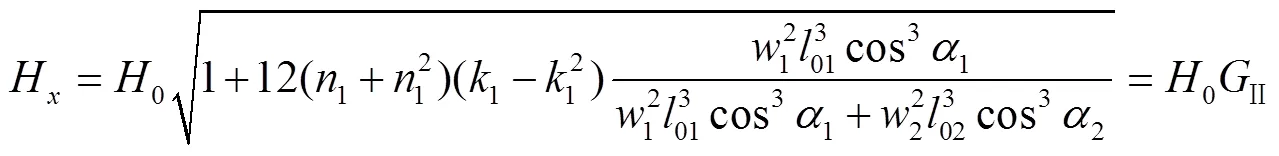
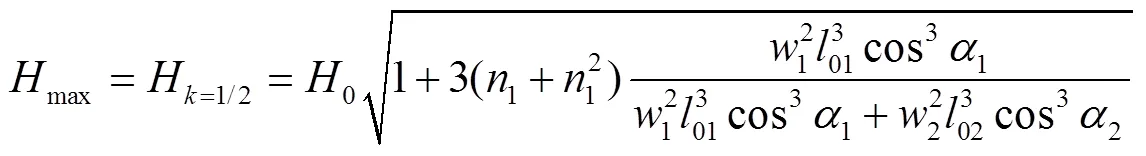
1.3 悬索的补正计算

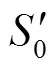
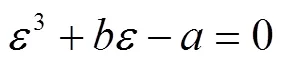
2 案例分析

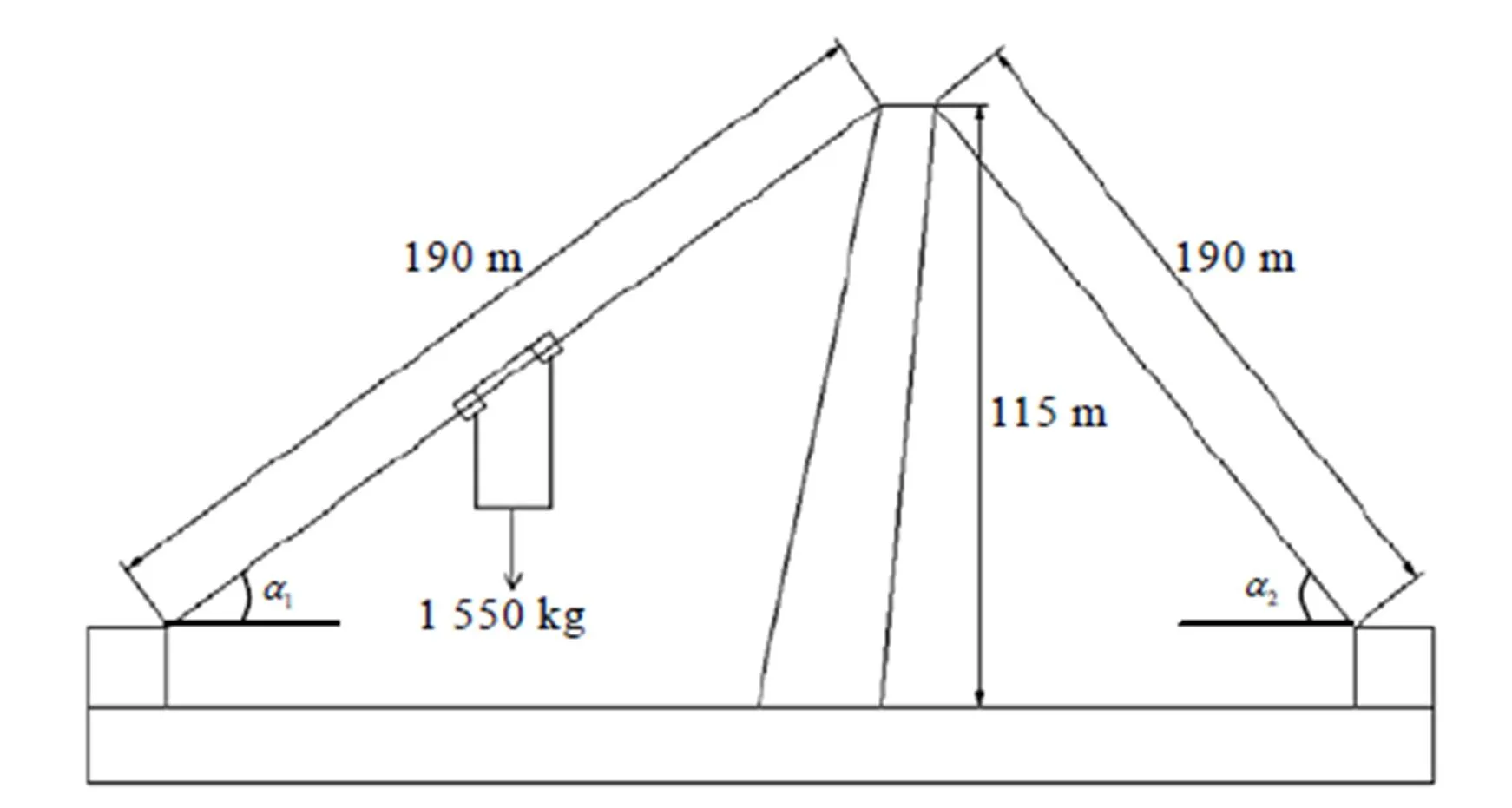
图5 某吊篮系统简图

2.1 计算步骤

按前述理论分析，案例的计算步骤如下：

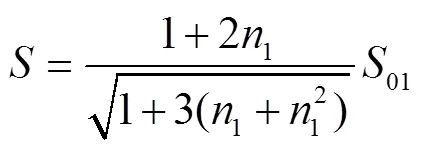
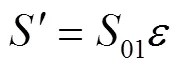
6）计算安全系数

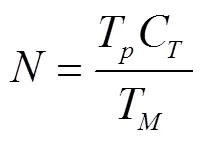
各种情况下的挠度可由挠度系数得到，见公式（3）.

2.2 计算结果

表1 主索计算结果

从表1可以看出，随着挠度的增大，索的拉力逐渐减少，安全系数不断提高. 因此，可以根据施工需要选择一个安全系数，并利用卷扬机进行拉力控制. 主索挠度的理论值也可与实际值进行比较，以充分保证施工的安全.

3 结语

本文采用静力平衡方程，并假设索的线性为抛物线，提出一种主索受力和变形的简易计算方法. 从案例分析的结果来看，该方法能得到主索的拉力、跨中的挠度和安全系数，能方便地对缆索吊装系统进行设计和施工控制，适用于一些简易的缆索吊装工程. 在以后的研究中，可将此计算方法同其他有限元方法的计算结果进行对比，并进一步简化计算过程和参数，以方便工程应用.

[1] 包立新，喻远良，林惠瑜. 索道吊装技术在悬索桥施工中的应用[J]. 重庆交通学院学报，2001, 20(3): 4-6.

[2] 郭爱兵，朱淑坤. 悬索吊装技术应用[J]. 河北水利水电技术，2004(2): 40-42.

[3] 刘延华. 简支梁缆索吊装结构的设计与施工[J]. 铁道工程学报，1997, 56(4): 19-27.

[4] 彭九州，黄太高，余钱华，等. 双跨118m钢筋混凝土箱形拱桥单肋吊装施工技术[J]. 中外公路，2005, 25(2): 104-106.

[5] 赵朝阳，杨文爽，李传习，等. 缆索吊装主索系统的受力分析算法与工作性能[J]. 广西大学学报：自然科学版，2010, 35(4): 615-620.

[6] 卢春玲，王强，邓康成. 龙胜岩门索桥悬索计算[J]. 桂林工学院学报，2004, 24(1): 48-51.

[7] 齐东春，沈锐利. 悬索桥空间缆索主缆线性的计算方法[J]. 铁道建筑，2013(4): 13-16.

[责任编辑：韦 韬]

Calculation of Stress and Deformation of Main Cables in Cable-hoisting Systems

CHENJun-song, LIUFei

(Wuxi City College of Vocational Technology, Department of Architecture Engineering,Wuxi 214153, China)

Given the fact that most of the popular theories of suspension cables are complicated and hard for constructors to control, this paper proposes a new and simple method to calculate the stress and deformation of cable-hoisting systems. A construction case is presented based on this new method. Tensile force, deflection and security coefficients are calculated accurately to verify the validity of the method. With this calculation method, both deformation and security coefficients of main cables in the cable-hoisting system with different tensile force can be obtained to help construction entities to choose the suitable suspension cable structure. The proposed method is believed to help construction entities to design cable hoisting systems and can serve as the basis for construction field control to improve construction safety.

cable-hoisting systems; main cables; stress; deformation

1006-7302（2014）04-0037-06

TU311.4

A

2014-04-11

江苏省高职院校高级访问工程师资助项目（2013FG004）；无锡城市职业技术学院院级重点课题项目（WXCY-2012-G2-002）

陈俊松（1984—），男，重庆涪陵人，讲师，博士，主要从事道路与桥梁工程的研究.