基于主因子模型的船用燃气轮机监测参数优化
袁 环,刘永葆
(海军工程大学 动力工程学院,武汉 430000)
气路故障诊断是燃气轮机的视情维护的重要技术之一,其中线性化故障诊断方法是气路故障诊断方法(GPA)中较常见的一类,由于其理论严谨、使用简单方便,获得广泛应用[1-2]。气路故障诊断过程都依靠于所选择的测量参数,因此测量参数选择的合理性也决定着故障诊断系统的诊断能力。目前测量参数选择方面的研究主要基于测量参数数目多于性能参数数目的前提下分析和优化,主要采用条件数[3]、奇异值[4]、敏感性[5]、最小估计方差[6]等选择指标进行最小冗余度的最优化诊断分析。而在实际燃气轮机装置的监控系统中,由于条件限制,测量参数个数一般都是少于性能参数个数,此时GPA方法就存在很大的技术应用瓶颈。本文在分析导致主因子模型诊断准确度下降的原因的基础上,建立某船用燃气轮机发生器的气路故障模型,运用敏感性、主成分分析方法,选取最优监测参数组合,并提高主因子模型的诊断准确率。本文的两个假设:(1)不考虑测量噪声的影响;(2)假设系统最多同时两个部件发生故障。
1 气路故障诊断的主因子模型方法
1.1 故障建模
通过对燃气轮机原数学模型在某工况下进行小偏差化,并引入故障因子,建立故障因子与测量参数之间的线性关系:

式中:Y为10×1维的测量参数偏差向量,X为8×1维的故障因子偏差向量,A为10×8维的故障系数矩阵。
该模型故障因子有:低压压气机折合流量δGCL、效率 δηCL;高压压气机折合流量 δGCH、效率 δηCH;高压涡轮折合流量δGTH、效率δηTH;低压涡轮折合流量δGTL、效率δηTL。可选择的测量参数有:低压压气机出口压力p2、出口温度t2;高压压气机出口压力p3、出口温度t3;燃烧室出口温度t4;高压涡轮出口压力p5、出口温度t5;低压涡轮出口压力p6、出口温度t6;低压轴转速nl、高压轴转速nh。
1.2 主因子模型
本文分析的是测量参数少于故障因子时,使用主因子模型方法进行故障诊断。
主因子模型的计算过程:
列举所有可能的主因子组合(n个故障因子中,人为假设p个故障因子不为0,其余都为0,假设不为0的故障因子即为主因子),每一个组合代表一种故障模式,由于有假设(2)存在,所以可能的组合数为,每一种主因子组合建立相应的选模型

Y为选择的测量参数偏量,X为主因子向量,B为对应主因子的故障系数矩阵。
对选择的模型使用最小二乘法求解:

对所有解计算故障相关性准则,本文故障相关性选为RSS准则:

将RSS与故障相关性准则阈值比较,由于本文不考虑噪声的影响,当主因子组合包含实际故障时,RSS≈0,阈值选为10-10,当RSS小于阈值时故障相关性成立。
对满足故障相关性准则的主因子组合使用合理性准则进行排除,得到合理解,合理性准则有故障偏差有界性和方向性。
对所有合理解求平均值得到最终解:

诊断结果的准确度可以用相似度S进行判断,相似度越接近1,诊断越准确:

影响主因子模型诊断精度的一个重要原因就是燃气轮机气路故障模型的系数矩阵中存在的多重共线性[2],多重共线性是由故障系数矩阵欠定和故障因子间的相关性两种原因造成的。多重共线性一方面导致最小二乘解的方差增大,另一方面会使得存在多解也即相似故障。选择合适的测量参数,可以有效减少多重共线性的存在,提高主因子模型故障诊断精度。条件数、方差膨胀因子等指标常用来描述超定矩阵的多重共线性程度,但不适用于欠定矩阵,所以无法作为测量参数少于故障因子时的参数选择指标。本文使用主成分分析方法研究故障系数矩阵的多重共线性,提供一种测量参数选择方法。
2 测量参数选择
在测量参数的选择中应该遵从以下几点原则:①所选测量参数能使故障诊断方法有效定位故障、估计故障程度;②测量参数对于所选的故障因子要有足够的敏感性,能够比较明显地反映故障因子的变化;③ 测量参数最好能够均匀地分布在发动机各个截面上,测量参数易于测量,减少成本。
2.1 主成分分析
相似故障由于具有和部件故障相同的测量值,其RSS值一般小于阈值,且合理性准则无法将其全部排除,所以合理解常出现相似故障,导致最终解的精度降低。由于假设(2)的存在,限制了主因子组合的因子数最多为4,本文通过相似故障的因子数进行排除,因子数大于4的相似故障不出现在主因子组合中。相似故障的因子数可以通过主成分分析得到。
对式(1)进行标准化(将故障方程中的各故障系数向量分别除以相应的长度使之成为单位向量)得到:

对标准相关阵HH求特征值和特征向量:

由式(9)可得:
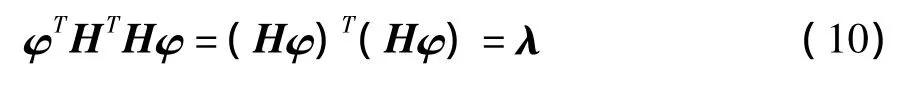
因此每一个为零特征值或近似为零的特征值都对应着一个多重共线性关系:
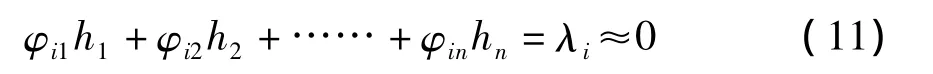
故障与对应的相似故障存在于多重共线性关系中。
为了提高主因子模型对相似故障的排除能力,选择的测量参数序列应使得相似故障包含更多的因子数,等同于要求故障系数矩阵中的多重共线性关系包含更多的因子数。本文以多重共线性关系包含的最小因子数多少作为测量参数选择指标。
将每个测量参数序列对应的故障系数矩阵中所有的多重共线性关系组成一个矩阵M:

式中:i为零特征值个数,n为故障因子总数。
将矩阵M化为最简形,矩阵第i行非零元素的个数即为该测量参数序列对应故障系数矩阵的最小因子数。
对候选的7参数序列、6参数序列、5参数序列使用主成分方法分析其多重共线性关系中所包含的最小因子数,如果最小因子数等于或少于5则排除该序列,分析发现并不存在最小因子数为7的序列,所以最终保留的测量参数序列所包含的多线性关系最小因子数都为6,7参数序列中有15种序列的最小因子数为6,6参数序列中有12种,5参数序列中有1种,综合考虑诊断有效性和成本因素以及系统余度要求,选择6个测量参数较为适宜。
2.2 敏感性分析
对于故障因子的微小变化,测量参数应该变化越大越好,也即越敏感越好,这样易于在故障早期就可以发现故障,及早做好维修策略,预防大的故障发生。测量参数的敏感性可以直接从故障系数矩阵得到,对于不同的故障因子按照测量参数变化值的绝对值大小进行排序就可以找到对单个因子最敏感的测量参数。
分析表明:t3对高压压气机效率最敏感,nh对高压压气机流量最敏感,而其它参数对这两个故障因子并不足够敏感,因此这两个参数应该选择;p3、nl、p2对其它故障因子变化非常敏感,可以作为备选参数。
2.3 综合选择
高压涡轮出口温度t5在实际应用中是个很重要的参数,常常用它来预警低压涡轮进口温度是否过热,一旦超过警戒温度,涡轮叶片就可能被烧毁,因此t5也应该被选择。由于燃烧室出口温度过高,在实际中不易测量,所以t4在这只作理论上的探讨,不能选为测量参数。考虑原则3,测量参数的均布原则,最终选择的测量参数序列为:低压压气机出口压力p2、高压压气机出口温度t3、高压涡轮出口温度t5、低压涡轮出口温度t6、低压轴转速nl、高压轴转速 nh。
3 算例分析
另外通过使用条件数作为标准选择了一个测量参数序列:p2、p3、t2、t3、nl、nh。比较了两种测量参数序列下主因子模型对18种故障类型的诊断能力,每种故障类型取100个故障样本,故障程度采用随机赋值的方法确定,赋值范围在-1%至-5% 之间,这18种故障分别是:(1)δηCL、(2)δηCH、(3)δηTH、(4)δηTL、(5)δGCL、(6)δGCH、(7)δGTH、(8)δGTL、(9)δηCLδGCL、(10)δηCHδGCH、(11)δηTHδGTH、(12)δGTLδηTL、(13)δηCLδGCLδηCHδGCH、(14)δηCLδGCLδηTHδGTH、(15)δηCLδGCLδGTLδηTL、(16)δηCHδGCHδηTHδGTH、(17)δηCHδGCHδGTLδηTL、(18)δηTHδGTHδGTLδηTL。两测量参数序列的故障诊断结果见表1。
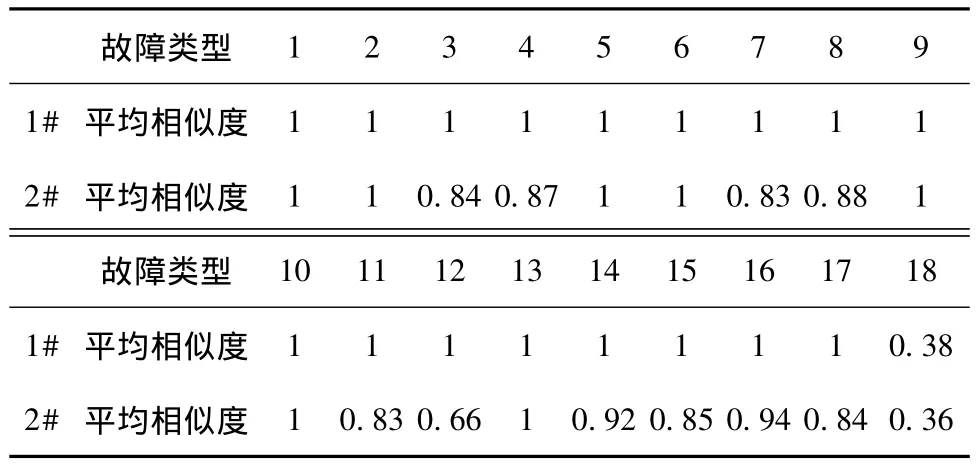
表1 两测量参数序列对18种故障类型的诊断能力
从表1可以发现,通过主成分分析方法选取的测量参数序列对各种类型的故障诊断能力都很好,且比使用条件数选取的测量参数序列2的诊断能力高。这说明对于测量参数数目少于故障因子数目时,由于相似故障的存在,条件数并不能作为测量参数的选择标准。序列1无法正确诊断故障18,是因为该故障对应的故障系数矩阵多重共线性严重,可以选择其它的测量参数序列进行诊断。计算测量参数序列1对应系数矩阵的条件数,cond(B)=64,这说明通过本文介绍的方法选择的测量参数序列组成的诊断系统对噪声的容忍性较好。
分析所选序列对前12种故障的敏感性,结果如图1、图2所示。包含的多重共线性所含因子数情况,可以预先判断该参数序列的诊断能力,并以此作为测量参数选择标准。结合敏感性分析,最终选择的测量参数序列故障诊断能力良好,提高了主因子模型的诊断精度,且测量参数敏感性较好,易于观察,测量噪声对由该序列组成的故障诊断系统影响较小。同时通过对比说明了条件数不能作为测量参数有限时的选择标准。

图1 单因子故障的敏感性检查

图2 双因子故障的敏感性检查
从图1可以发现,每类单因子变化-1%时,都有测量参数变化较大,接近或超过1%,例如故障1变化-1%时,p2变化1.1%,故障2变化-1%时,t3变化1.2%。图2中显示了双因子故障变化值为-1.5% 和-3%时测量参数的变化,测量参数变化较为明显,例如故障9变化(-1.5%、-3%),p2变化2%,nl变化3%。该序列对于所有类型的故障的敏感性都较好,因此各种类型的故障都是可以观察的。
4 结论
主因子模型方法可以利用较少的测量参数诊断发动机故障,但测量参数有限会导致多重共线性严重,影响诊断精度。合理选择测量参数可以提高诊断精度,通过主成分分析方法分析故障系数矩阵所
[1]Urban.L.A.Gas Path Analysis Applied to Turbine Engine Condition Monitoring[J].Journal of Engineering for Power.1972,10(7):400-406.
[2]范作民,孙春林,白杰.航空发动机故障诊断导论[M].北京:科学出版社,2004.
[3]Ph.Kaboukos,P.Oikonomou,A.Stamatis,and K.Mathioudakis.Optimizing diagnostic effectiveness of mixed tur-bofans by means of adaptive modelling and choice of appropriate monitoring parameters[C].Ageing Mechanisms and Control Specialists'Meeting on Life Management Techniques for Ageing Air Vehicles,Manchester,UK,October 2001.
[4]蒲星星,刘尚明,蒋洪德.重型燃气轮机状态能观度分析及其在故障诊断中的应用[J].中国电机工程学报,2012,32(2):117-122.
[5]S.O.T.Ogaji,Sampath S.,R.Singh,and S.D.Probert.Parameter selection for diagnosing a gas-turbine's performance-deterioration[J].Applied Energy,2002,73(1):25-46.
[6]Simon D.L.,Donald L.A Systematic Approach to Sensor Selection for Aircraft Engine Health Estimation[R].[NASA/TM-2009-215839].

