列车间不确定性资源请求冲突的预测方法

郭竞文，孟令云，冉 锋，陈瑞金

（1. 北京交通大学 交通运输学院，北京 100044；2. 北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044；3. 天津南环铁路有限公司 总工室，天津 300202；4.天津南环铁路

有限公司 安监室，天津 300202）

0 引言

列车按照列车运行图规定的作业时分在路网上运行，因受到外界扰动 ( 如恶劣天气、设备故障 ) 的影响，列车实际运行时间较图定作业时分会发生偏离。当偏离量超出一定范围时，该列车会与其他列车发生资源请求冲突，即 2 列车同时请求使用同一技术设备 ( 以下简称冲突 )。

国外对不确定性冲突的研究尚处于起步阶段，Hansen 通过研究轨道区段锁闭时间和资源请求冲突的概念，为不确定性冲突的研究提供相关理论基础[1-3]；Fabris 等[4]实际模拟列车计划占用区间时间范围和实际占用区间时间范围之间的差异，计算出冲突发生的概率，探讨列车间不确定性冲突的形成过程；Meer 等[5]明确运行时间的 3 个要素，阐述区间内 4 种不同情况下的列车运行冲突，用不同曲线拟合延迟时间与到达延误之间的关系；Medeossi[6]利用轨道区段锁闭时间表述列车运行的实际过程，绘制列车不同运行状态的运行时间分布图，为不确定性冲突的概率计算提供基础。国内对于不确定性冲突的研究相对较少，但通过数据分析处理对研究列车运行现状具有一定进展。王军等[7]提出对实测数据的处理方法以便于标定参数和进一步研究；陈军华等[8]充分利用现有铁路相关系统的数据，提出基于铁路信息化数据的自动化查标方法，解决原始数据获取及多元数据处理等关键问题。

综上所述，列车间不确定性冲突预测仍然需要进一步研究，为提高列车间冲突预测的准确性、疏解冲突、制订更加高效的列车运行调整方案提供可靠依据。发车间隔时间小于最小间隔时间的列车冲突如图 1b所示。

图1 列车间冲突的产生

由于列车实际停站时分和区间运行时分所受到的扰动具有不确定性，从而使晚点时间未必大于缓冲时间，从而存在冲突不确定性。通过对历史数据进行分析，列车 1 在车站 a、b 的实际运行线构成 1 个线束，列车 1 在 b 站的到站时间概率服从一定规律的函数分布，列车间不确定性冲突的产生如图 2 所示。由于列车 1 在 b 站的到达时刻具有不确定性，其与列车 2 在 b 站的到达间隔时分不一定满足最小间隔时分，从而列车 1 与列车 2 的到达冲突具有不确定性。将这种可能发生的冲突称为不确定性资源请求冲突，简称不确定性冲突。

图2 列车间不确定性冲突的产生

1 列车间不确定性冲突

1.1 不确定性冲突

列车 1、2 先后从a站发车，最小发车间隔时间为hmin，图定发车时间为d1a和d2a，发车间隔时间为h=d2a-d1a＞hmin，发车间隔时间大于最小间隔时间的列车冲突如图 1a 所示。当列车 1 在 a 站受到客流波动或其他因素影响使其实际发车时分d1a’＞d1a即发车晚点时，列车 1 和列车 2 之间的实际发车间隔时间h’＜hmin，列车 1、2 在 ab 区间发生冲突，

1.2 列车间不确定性冲突影响因素

列车间不确定性冲突的影响因素主要分为冗余时间、机车车辆 ( 车底 ) 和其他因素 3 个方面。

1.2.1 冗余时间

在正常情况下，列车按照运行图给定的作业时分运行，但是实际运行时不可避免会发生一些难以预知的情况，如机车车辆故障、固定设备故障等，上述情况往往会导致列车不能按照预定的时刻表运行。冗余时间对不确定性冲突的影响如图 3 所示，当运行图设定的冗余时间tr无法吸收突发情况造成的晚点d时，就会发生冲突。因此，冗余时间是影响不确定性冲突发生的关键因素之一。

1.2.3 其他因素

图3 冗余时间对不确定性冲突的影响

（1）天气因素。在雨雪天气下，轨道被淋湿后，轮轨间的粘着性降低，增加列车加速和制动难度，与正常天气条件相比，其运行时间会发生较大偏离[9]。由于这种偏离具有不确定性，从而引发不确定性冲突。

（2）人员素质。调度员制订列车运行调整计划的优劣与机车乘务员操纵技术水平的高低均直接影响列车实际运行时间。

（3）高峰时段。在高峰时段，较多旅客选择进入铁路运输网络，停靠站上下车的旅客人数增加，从而延长停站时间，导致晚点，容易发生冲突。

上述因素使列车运行时间具有不确定性，从而使列车间冲突的发生具有不确定性，影响不确定性冲突发生的概率。

2 列车间不确定性冲突预测的方法

1.2.2 机车车辆(车底)

在运行过程中，普通列车由于运行途中停靠站点较多，加之受其他列车晚点或停开等事件的影响，容易产生晚点，从而发生不确定性冲突；而快速列车技术速度高、停站少、“赶点”能力强，抗扰动能力强，不容易产生不确定性冲突。机车车辆对不确定性冲突的影响如图 4 所示，列车 1 经过“赶点”在预计晚点运行线之前到达，从而减少冲突发生的概率。

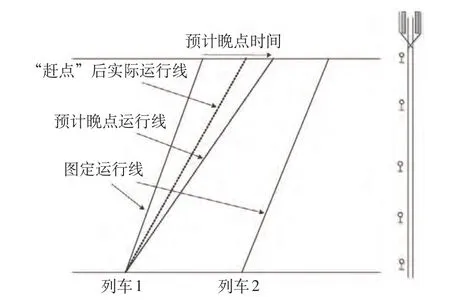
图4 机车车辆对不确定性冲突的影响

基于区间运行时分描述不确定性冲突的方法具有数据易获的优点，但是有以下缺点：①基于列车区间运行时间计算不确定性冲突的粒度较粗；②计算复杂，前行列车的发、到时间直接影响后行列车的运行，相关系数不确定；③容易出现无效数据影响计算结果。而基于轨道区段锁闭时间预测列车间不确定性冲突的方法具有以下优点：①计算粒度较细；②计算简单，利用前方列车释放轨道区段时间和后方列车锁闭轨道区段时间进行计算，简单明了；③异常数据剔除简单。为此，通过轨道区段锁闭时间和资源请求冲突 2 个概念对列车间不确定性冲突建模。

轨道区段锁闭时间指从该轨道为允许某列车“独占”而锁闭的时刻开始至该轨道区段解锁而允许其他列车占用为止的时间范围。资源请求冲突指2 列列车或多列列车在同一时刻请求占用同一行车资源，也可以指前方列车所占用的行车资源 ( 如轨道区段等 ) 尚未释放，后方列车开始请求占用同一段的行车资源而发生的冲突[10]。列车 1、2 存在资源请求冲突时的锁闭时间示意图如图 5 所示 ( 带阴影的方框为轨道区段锁闭时间，2 个阴影重叠的区域为资源请求冲突 )。

基于轨道区段锁闭时间预测列车间不确定性冲突主要通过描述列车运行时相邻列车间轨道区段锁闭时间的关系，从而判断列车之间是否产生不确定性冲突，具体步骤如下。

图5 列车 1、2 存在“资源请求冲突”时的锁闭时间示意图

（1）统计列车在轨道区段的锁闭时间。针对某一轨道区段和列车，考察列车在轨道区段上一段时间 ( 如 1 个月 ) 的锁闭时间，并予以叠加，得出颜色不同的区域。颜色的深浅表示列车在该轨道区段锁闭时间可能性的大小，颜色越深表示可能性越大，单次列车轨道区段锁闭时间的叠加如图 6 所示。以轨道区段a为例，矩形方框Ra1表示列车2009 年 2 月 1 日在轨道区段a的锁闭时间，将 1 个月内列车每天在该轨道区段的锁闭时间叠加，得到列车在轨道区段a的锁闭时间。

图6 单次列车轨道区段锁闭时间的叠加

（2）确定不确定性冲突发生区域。针对某一轨道区段的相邻 2 列列车，考察列车在轨道区段上一段时间内 ( 如 1 个月 ) 的锁闭时间，并且予以叠加，若 2 列列车的叠加区域发生重叠，则重叠区域为不确定性冲突形成的位置，相邻 2 次列车轨道区段锁闭时间的叠加如图 7 所示。在轨道区段b中，将 1 个月内相邻 2 列列车每天在该轨道区段的锁闭时间叠加，重叠区域 ( 虚线框内 ) 即为不确定性冲突发生区域。

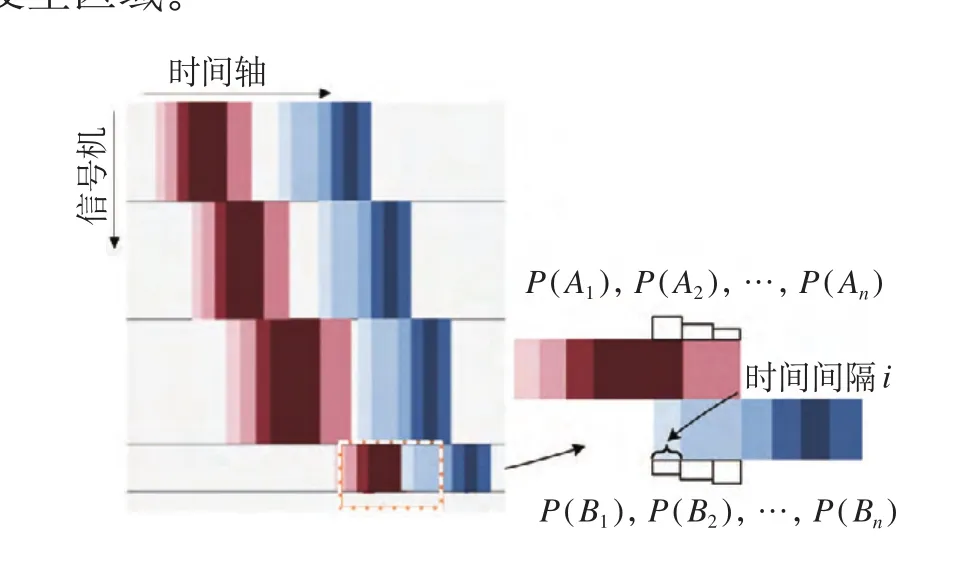
图7 相邻 2 次列车轨道区段锁闭时间的叠加

（3）利用离散数据计算不确定性冲突发生概率。设事件L表示不确定性冲突发生，则其概率计算公式为

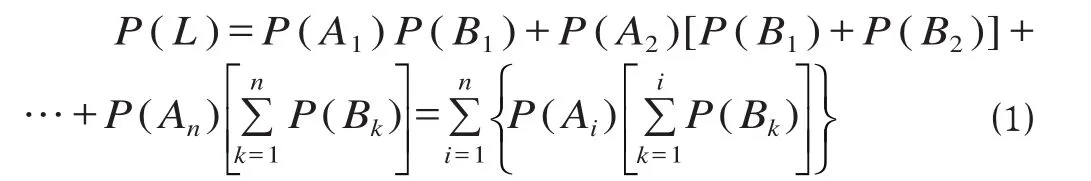
式中：Ai为前方列车a在时间范围i内占用轨道区段，B1，B2，…，Bi为后方列车b占用轨道区段的时间不晚于前方列车a( 见图 7 )。为简便计算，将时间间隔i划分为相等的范围和区域。

（4）利用拟合曲线计算不确定性冲突发生概率。根据图 7 中柱状图利用 Matlab 软件拟合曲线，前后 2 列车的轨道区段锁闭时间分布如图 8 所示。蓝线为前行列车的轨道区段释放时间rj，绿线为后方列车的轨道区段锁闭时间dj+1，二者重叠的阴影部分为后车请求使用轨道区段的时间dj+1小于前车释放该轨道区段时间rj的概率。

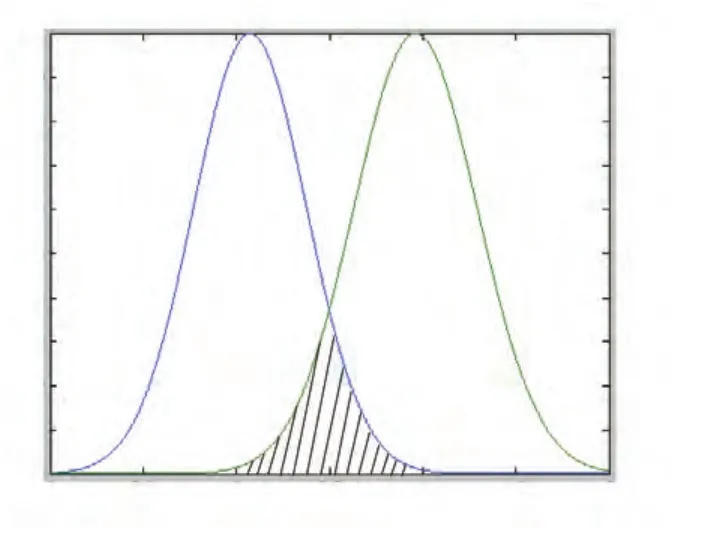
图8 不确定性冲突的概率表示

因此，不确定性冲突概率计算公式为

由于rj和dj+1近似服从正态分布，其联合概率密度函数计算公式为

式中：μ1和μ2分别为rj和dj+1的期望；σ1和σ2分别为rj和dj+1的标准差；ρ为rj和dj+1的相关系数。

则不确定性冲突的发生概率计算公式为

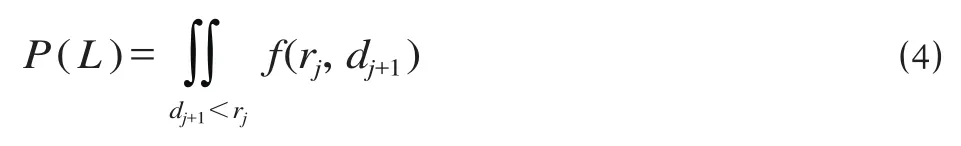
3 实例分析

3.1 数据结构

以 2009 年 2 月某铁路沿线各车站接发列车时刻和列车通过各信号机的时刻记录为例，其占用类型、占用名称、开始占用时间及结束占用时间如表1 所示。其中，用每个轨道区段中最后 1 节钢轨的结束占用时间减去第 1 节钢轨的开始占用时间，得到 1 个轨道区段的区段锁闭时间 ( 如 160-102 = 58 s )。

表1 轨道区段锁闭时间与每节钢轨开始占用时间与结束占用时间

3.2 异常数据处理

对给定的数据集合进行统计分析并绘制分布图，然后根据分布密集程度确定“有用”数据的范围，与给出范围“偏离”的对象被认作异常点。在研究过程中，根据数据特征，采用基于统计的异常数据处理方法，只保留在正常范围内波动的数据，将范围外的数据定义为异常数据，对其进行删除。

3.3 列车间不确定性冲突预测

选用 A、B 次列车 1 个月内 m 站到 n 站的线路数据进行算例验证。

（1）统计列车在轨道区段的锁闭时间。提取A、B 列车 1 个月内从出发信号机 ( 54 号信号机 ) 至到达信号机 ( 316 号信号机 ) 之间轨道区段锁闭时间的数据。由于轨道区段锁闭时间可以用区间的实际占用时间表示，因而每 2 个信号机之间提取的轨道区段实际占用时间即为轨道区段的结束占用时间dj与开始占用时间rj的差。

（2）确定不确定性冲突发生区域。将所得数据进行分组，选用合适的时间间隔i。根据统计学原理，时间间隔过大或过小，均会导致不确定性冲突的计算不准确。因此，通过对数据进行分析，选取时间间隔 30 s，A、B 次列车在 362 号和 316 号信号机之间每个时间范围内轨道区段锁闭时间密度如表 2 所示。

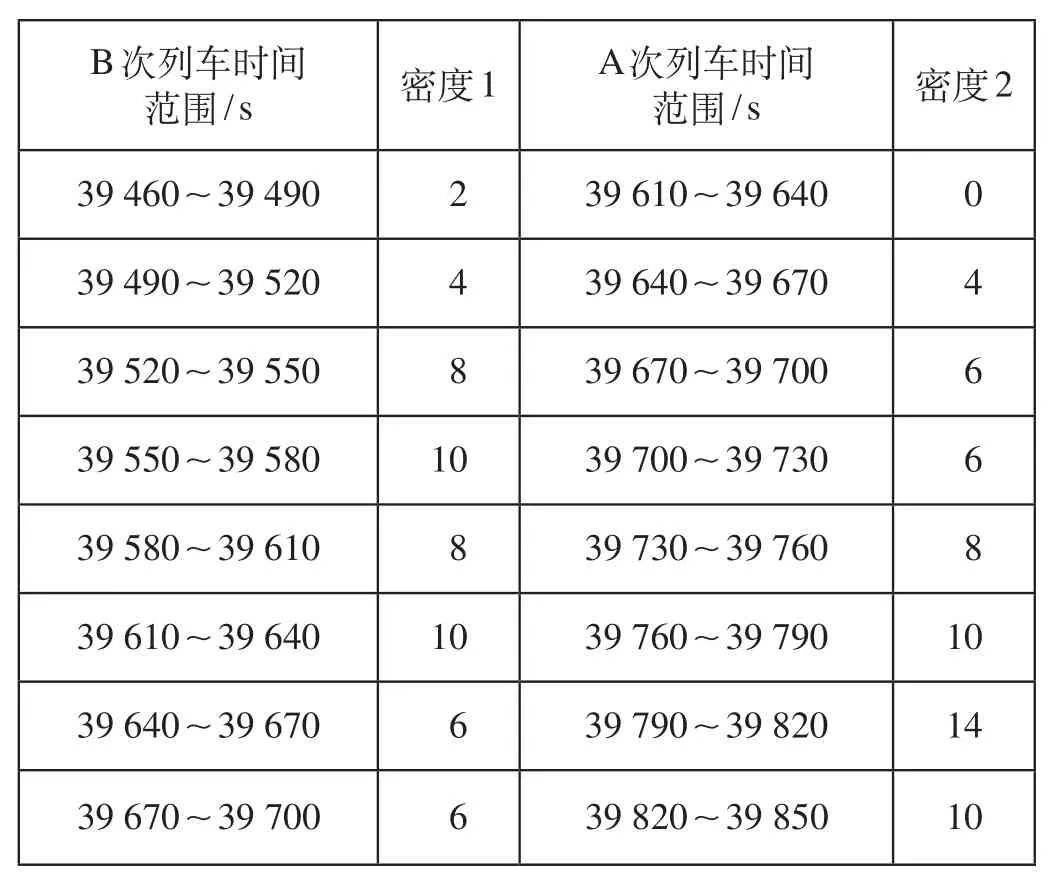
表2 轨道区段锁闭时间密度

同理，对出发信号机与到达信号机间的另外3 个轨道区段锁闭时间的数据进行处理，然后根据所得数据对轨道区段锁闭时间进行叠加，得到不确定性冲突如图 9 所示。

图9 A、B 次列车列车的不确定性冲突

（3）利用离散数据计算不确定性冲突发生概率。由于时间轴的绘制刻度线间隔为 30 s，图 9 中橙色方框处为不确定性冲突发生的位置。利用⑴式计算得到：P(L) ≈ 25.9%，即 A、B 次列车之间不确定性冲突的概率为 25.9%。

（4）利用拟合曲线计算不确定性冲突发生概率。设相关系数ρ为 1，采用⑵式至⑷式计算得出A 次列车锁闭 362 号信号机的平均时间μ1、方差σ1，B 次列车释放 362 号信号机的平均时间μ2、方差σ2，从而得到

综上所述，通过人工提取数据并进行分析处理，剔除异常数据，对 A、B 次列车之间的不确定性冲突进行计算，得到其冲突概率为 24.9%。对离散型数据计算结果与拟合曲线后结果进行比较，数据存在误差，但是偏离不大，原因在于：①在离散型数据处理中对数据进行人为分组存在误差；②列车A、B 之间可能存在相关性导致相关系数不为 1；③数据量较少，无法得到最优拟合。

4 结束语

通过定义不确定性冲突，提出不确定性冲突判断的方法，最后进行实例验证。为制订更加高效的列车运行调整方案，提高列车运行安全性提供更可靠的依据，下一步研究方向是进一步描述列车间不确定性冲突在运行图上的传播过程，并且对列车间不确定性冲突的疏解问题进行研究。

[1] Corman F，D’Ariano A，Hansen I. Disruption Handling in Large Railway Networks[C]//Beijing Jiaotong University. 12th International Conference on Computer System Design and Operation in Railways and Other Transit Systems. Beijing：WIT Press，2010：629-640.

[2] Hansen I. Railway Timetable &Traffic [M]. Hamburg：Eurailpress，2008.

[3] Hansen I. Railway Network Timetabling and Dynamic Traffic Management[J]. International Journal of Civil Engineering，2010，8(1)：19-32.

[4] Fabris S，Longo G，Medeossi G. An Implementation of Stochastic Blocking Times to Support Timetable Planning[J].Journal of Rail Transport Planning & Management，2011，1(2)：1-13.

[5] Meer D，Goverde R，Hansen I. Prediction of Train Running Times Using Historical Track Occupation Data[C]//Yoshi Hayashi. World Conference on Transport Research. Lisbon：Case Studies of Transport Policy，2010，1-22.

[6] Medeossi G. Stochastic Blocking Time Modeling [C]// I.A.Hansen. The 5th International Seminar on Railway Operations Modelling and Analysis. Copenhagen：ELSEVIER，2013：1-13.

[7] 陈军华，张星臣，徐 彬，等. 信息化条件下车站作业标准时间查定方法研究[J]. 交通运输系统工程与信息，2011，11(6)：119-123.

[8] 王 军，张星臣，张 懿，等. 基于数据挖掘的运行图参数查定与修正方法[J]. 中国铁道科学，2011，32(7)：117-121.

[9] D’Ariano A，Pacciarelli D，Pranzo M. A Branch and Bound Algorithm for Scheduling Trains in A Railway Network[J].European Journal of Operational Research，2007，183(2)：643-657.

[10] 孟令云，Goverde R. 基于实际数据分析的列车晚点传播过程构建方法和实例[J]. 北京交通大学学报，2012，36 (6)：15-20.