成网条件下高速铁路动车组运用计划优化模型研究

闻克宇，何必胜，徐 林

（1. 铁道部经济规划研究院 运输咨询部，北京 100038；2. 北京交通大学 交通运输学院，

北京 100044；3. 杭州杭港地铁有限公司 运营支持室，浙江 杭州 310000）

动车组运用计划的编制受到多种因素的影响，如高速铁路路网结构、列车运行计划、运输组织模式、运输管理体制等，而编制一个适应国情、路情的动车组运用计划，有助于促进我国高速铁路运营生产效率的提高。动车组运用计划编制是一种多车场的车辆调度问题，与其他运输方式不同，动车组运用计划还包括日常检修计划。国内不少专家和学者都在动车组运用计划领域进行深入的探索，取得了一定的理论成果[1-5]。但是，随着我国高速铁路逐渐成网，动车组运用计划优化问题更为复杂，因而需要进一步优化和协调动车组运用与检修的关系。由于成网条件下的动车组运用计划与既有动车组运用计划存在较大区别，因而结合成网条件下动车组运用计划的特点和我国国情、路情，研究有效优化方法。

1 成网条件下动车组运用计划描述

在列车运行图确定后，动车组运用计划主要研究由哪些动车组承担铁路运输任务。为了确保动车组的安全运行，动车组运用计划需要将检修计划纳入日常运营。因此，动车组运用计划应综合考虑动车组检修任务、动车组的种类和数量、运行图图定任务等因素，不断优化动车组运用总成本，并且保证动车组运用计划的鲁棒性和稳定性。以我国CRH 系列动车组为例，其检修指标分为 5 级，如表1 所示[6]。

动车组运用可以分为固定区段和不固定区段 2种类型。固定区段的动车组运用相对比较简单，但会增加动车组运用的成本。为此，主要研究在不固定区段使用方式下动车组的运用优化问题，即动车组完成 1 次运输任务后，根据一定目标选择接续任务。为了研究多个动车段 ( 所 ) 条件下的不固定区段动车组运用问题，通过综合考虑动车组检修计划，作出以下假设：①动车组从所属动车段 ( 所 ) 出发，在该计划结束时必须返回原动车段 ( 所 )；②动车组使用方式为不固定区段使用；③一级检修和二级检修任务包含在动车组计划内。

2 构建时空网络

为了避免随着运输任务规模的增加，动车组运用计划优化模型的规模急剧增加，需要将动车组运用优化问题简化，为此引入时空网络[7]。时空网络将复杂的网络流规划问题的建模求解带入由“时间”轴和“空间”轴构成的二维空间，为动车组运用计划优化问题提供了一种有效的方法。

考虑以运输任务为节点，根据相邻运输任务之间的函数关系ω(s，t) 在节点之间建立相应的弧，从而构建出时空网络。根据运输任务的属性，通常将运输任务分为 3 类：运输作业、基地作业、检修作业。同时，将函数关系分为以下 3 种情况：相邻运输作业之间的函数关系、运输作业与基地作业之间的函数关系、运输作业与检修作业之间的函数关系。在考虑开始地点、到达地点、开始时刻、结束时刻、发生地点、持续时间、运行里程、需要的动车组数量等时空属性后，可以根据以下步骤建立动车组运用的时空网络。

步骤 1：基于给定的运输任务集合R，对应不同类型的运输任务，建立与之相应的作业节点：运输作业节点、基地作业节点、检修作业节点，并且对应每一个作业开始时间、结束时间分别建立 1 对作业开始节点、作业结束节点。这 3 种作业节点的集合被记为V。

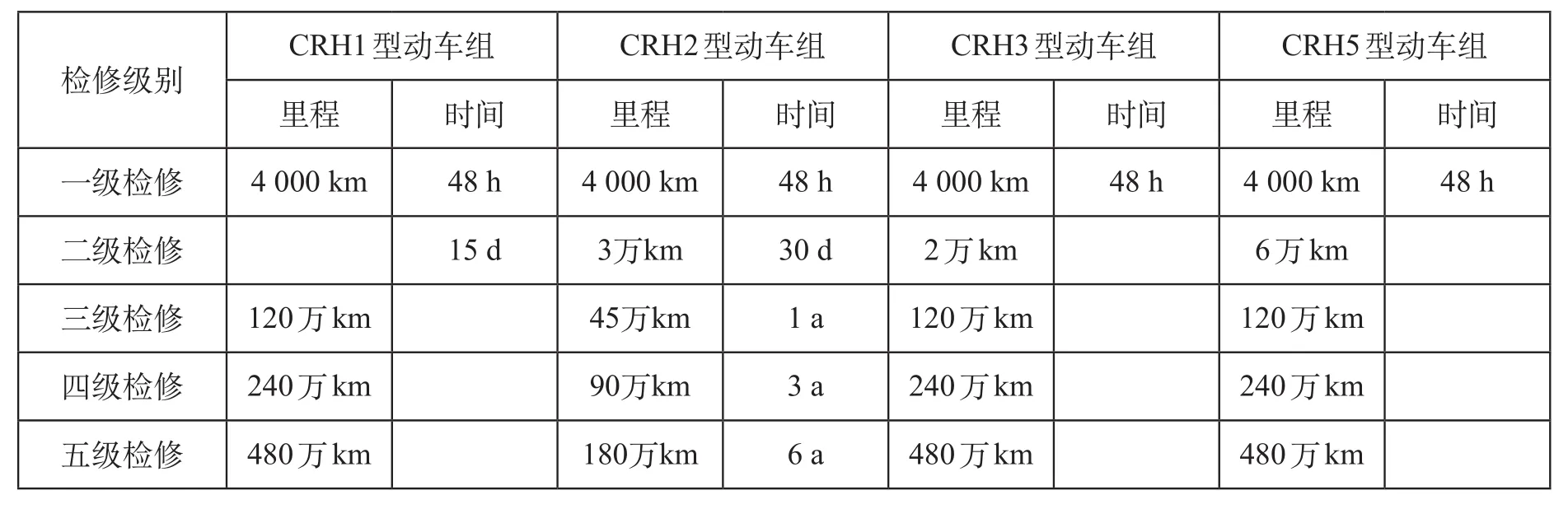
表1 CRH 系列动车组运用检修指标

步骤 2：根据运输任务的类型建立以下 4 类弧：①运输作业弧：动车组必须完成的运输作业任务，包含起讫节点等信息；②接续弧：动车组完成上次运输作业后继续下次运输作业过程中所走行的路径 ( 包含等待下一作业时间 )；③出入基地弧：动车组完成任务后出入车站或动车段 ( 所 ) 产生的行走轨迹，其特点就是将任务节点连接起来，以使动车组在任务间转换；④检修作业弧：动车组必须完成的检修作业任务，包含了起讫节点等信息。

在列车运行图基础上构建的动车组运用时空网络图如图 1 所示。在图 1 中，任意 1 条从计划开始时间到结束时间的完整的路径即可以看作 1 个动车组的交路。

对变量定义如下。

（1）s为车站，S为车站集合，则有s∈S。不办理始发终到作业的车站不影响动车组运用计划。因此，该集合内只包括办理始发终到作业的车站。

（2）k为动车段 ( 所 )，K为动车段 ( 所 ) 集合，则有k∈K。部分车站有相邻的动车段 ( 所 ) 用于动车组的检修，则设sk为配备有动车段 ( 所 ) 的车站，有sk∈Sk∈S。设Ck，1为动车段 ( 所 ) 1 天的一级检修能力，Ck，2为动车段 ( 所 ) 1 天的二级检修能力，Nk为动车段 ( 所 ) 的动车组数量。

（3）l为运用任务，Al为运用任务集合，则有l∈Al。l存在到达节点va，l和出发节点vd，l，其中：va，l∈Va，l，所处地点为sa，l，时间为ta，l；vd，l∈Vd，l，所处地点为sd，l，时间为td，l。l对应成本为wl。

（4）m为检修任务，Am为检修任务集合，则有m∈Am。m分为一级检修任务和二级检修任务，则有一级检修任务m∈Am，1二级检修任务m∈Am，2。出入动车段 ( 所 ) 对应有开始维修节点vb，m和结束维修节点vf，m，其中：vb，m∈Vb，m，地点为sb，m，时间为tb，m；vf，m∈Vf，m，地点为sf，m，时间为tf，m。若检修任务m发生在动车段 ( 所 )k则有γm，k= 1，否则为γm，k= 0。m对应成本为wm。

（5）c为接续弧，Ac为接续弧集合，则有c∈Ac。c用于连接l的任务终点和l'的任务起点，接续弧可以认为是Ac= {(l，l')|ta，l+ε＜td，l '，l∈Al，l'∈Al}，即只要l的任务结束时间与作业时间ε之和小于任务l'的任务开始时间，2 个任务之间就可以建立接续关系，生成接续弧。其中：若sa，l=sd，l'则为本地接续，若sa，l≠sd，l'则为异地接续。动车组夜间停留在车站或动车段 ( 所 ) 可以看作是一种接续弧，都可以理解为在车站驻车。c对应成本为wc。

（6）i，o分别表示入弧和出弧，入弧i∈Ai，出弧o∈Ao。i，o用于描述动车组进出车场走行的情况，连接的是运用任务和检修任务，由于只要动车组所在的车站配备有动车段 ( 所 )，动车组就能进出动车段 ( 所 )，因而在任意sk，当动车组需要进行检修时入弧即可产生，当检修完成时出弧也就产生。i，o对应成本分别为wi，wo。

图1 动车组运用时空网络图

（7）τ∈T为规划周期，τ代表第几天。

（8）e为动车组，Ek为动车组集合，动车段( 所 ) 都有相应配属的动车组，因而有e∈Ek。

（9）综上所述，有A=Al∪Ac∪Am∪Ai∪Ao，V=Va，l∪Vd，l∪Vb，m∪Vf，m，共同构成动车组运用时空网络G= (V，A)。在第τ天内，动车组可以分为2 类，一类是完成任务的动车组，另一类是没有进行任何任务的动车组。对于有任务的动车组e在G中存在可能的路径集合为p∈Pk，即为动车组e的交路段，所有动车组可能交路段生成路径集合Pk∈P。交路段包括列车运用任务和检修任务，以及连接它们的接续弧、入弧和出弧。

对于 2 个同级别的相邻的维修任务而言，中间的运行长度或时间必须小于该级别的规定，如 2 个一级检修任务间的运行距离和时间要小于一级检修中所规定的 4 000 km 和 48 h。因此，对路径p中所包含的检修弧按照时间顺序进行排序，一级检修任务集合Am，1，p，二级检修任务集合Am，2，p，m'为m的下一个同级检修任务。对于路径p中的每一个节点，还需要保存路径的走行时长tp，v和走行距离dp，v，其中v代表节点，用于进行检修状态识别。路径p对应的成本wp为

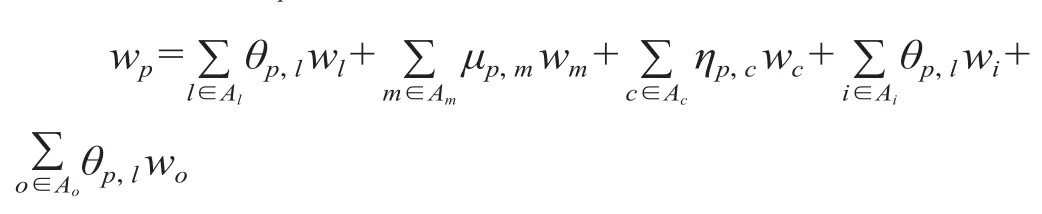
式中：θp，l为 0-1 变量，表示运用任务l是否在路径p上，θp，l= 1 代表l在p上，θp，l= 0 则反之；μp，m为 0-1 变量，表示检修任务m是否在路径p上，μp，m= 1 代表m在p上，μp，m= 0 则反之；ηp，c为 0-1 变量，表示接续弧c是否在路径p上，ηp，c= 1 代表c在p上，ηp，c= 0 则反之。

动车组运用时空网络，需要注意以下方面。

（1）完成 1 次运用任务到达车站后，动车组必须进行简单整备作业才可继续进行下次运用任务，即接续弧的时长必须大于整备作业时间ε。

（2）时空网络的优点就是能够减少接续弧数量。

（3）合理利用动车段 ( 所 ) 的检修能力能够有效减少动车组在动车段 ( 所 ) 的停留时间，进而提高动车组的使用效率。因此，要求 1 天内动车段 ( 所 )所进行的检修任务不超过动车段 ( 所 ) 的检修能力。{m|1440τ≤tb，m≤ 1440 (τ+1)，m∈Am，1} 代表第τ天的一级检修任务集合，{m| 1440τ≤tb，m≤1440 (τ+1)，m∈Am，2} 代表二级检修任务集合。

（4）动车组到达车站时，可以选择进入动车段 ( 所 ) 或在车站等待，若直接进入动车段 ( 所 )，出、入弧的成本均为定值，完成检修任务时，动车组在动车段 ( 所 ) 等待运用任务开始。因此，成本应为接续弧加上出弧的成本。

3 成网条件下动车组运用计划优化模型

以路径费用最小为目标函数，建立动车组运用计划优化模型为

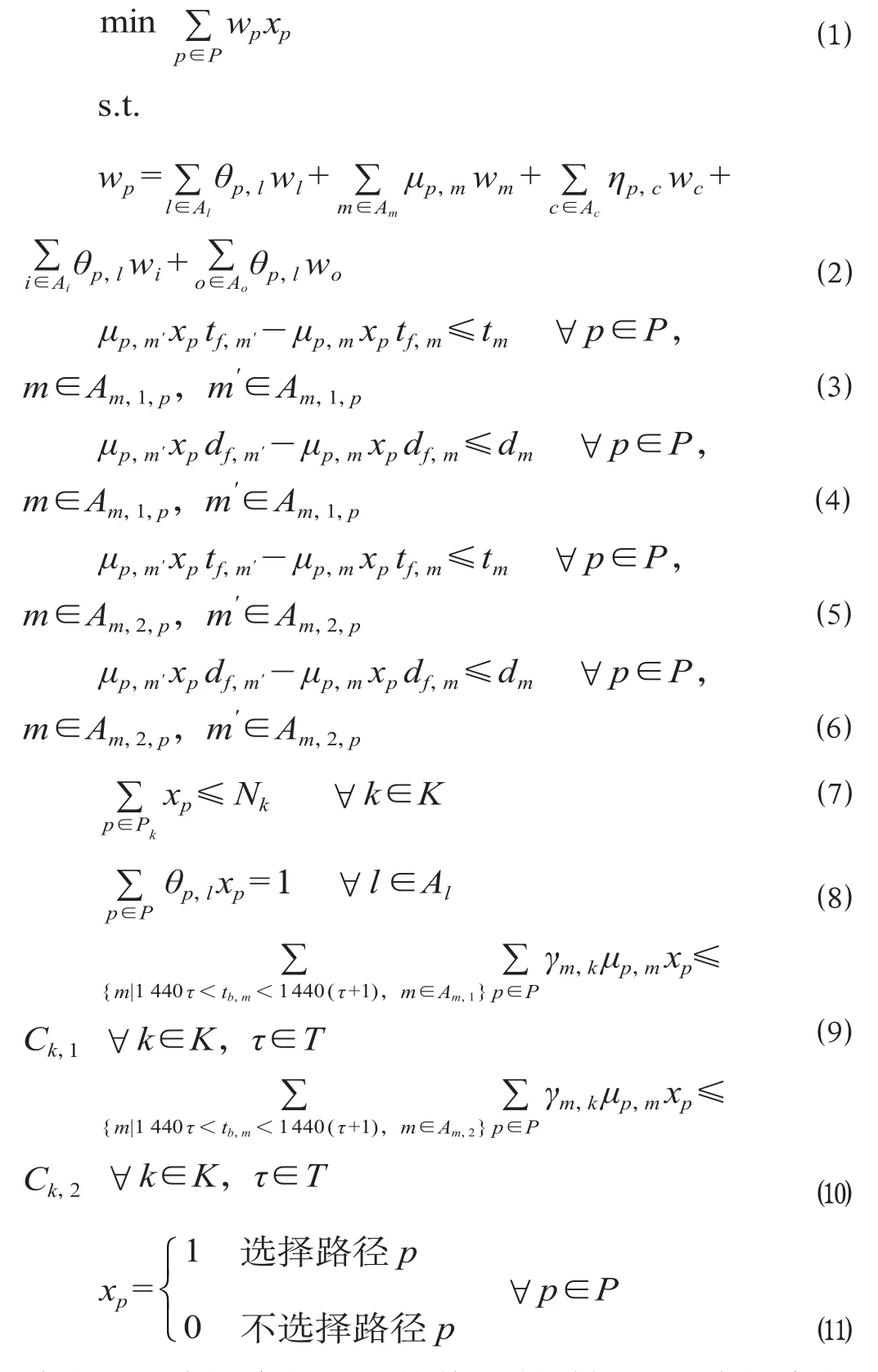
式中：tm为相应级别的检修限制时间；dm为相应级别检修限制距离。

⑴式为目标函数，该模型以动车组在运用过程中走行路径的总费用最小为目标。⑵式为走行费用计算方法。⑶式至⑹式为动车组的检修要求约束，必须在运用中按照要求完成一、二级检修，其中：⑶式为一级检修的时间要求，⑷式为一级检修的里程要求，⑸式为二级检修的时间要求，⑹式为二级检修的里程要求。⑺式为动车组运用数量上限，动车组运用数量不能超过动车段 ( 所 ) 存有的动车组数量。⑻式要求运用任务只能由 1 辆动车组完成；⑼、⑽式为动车段 ( 所 ) 一、二级检修能力约束。⑾ 式为变量约束要求，xp为 0-1 变量。

4 算法设计

通过分析成网条件下动车组运用计划的优化问题，采用大规模邻域搜索算法 ( Large-scale Neighborhood Search Algorithm ) 进行求解。为了进行邻域搜索，运用数字串对动车组交路段进行描述，假设动车组交路的编码形式为eX(l，k)，其中，X= 0 或 1，X= 0 代表进行任务作业，X= 1 代表进出动车段 ( 所 ) 作业。

为了缩小动车组运用问题的规模，同时保持计算精度不受影响，在构造初始解时提出班组的概念，即在给定配属动车组数量Nk的情况下，以T为周期用n个班组周期性分配完规定的u个任务。其中n=Nk/T。例如：线路规定配属 100 个动车组，周期为 10 天，每天 160 个任务，则需要编制 100 个动车组在 10 天内完成 1 600 个任务的计划。但是，如果以 10 天为周期分为 10 个班组，每个班组 10 个动车组来运行，让动车组周期性循环套跑，则只需要安排 10 个动车组在 1 天内完成 160 个任务的计划，其他班组按照这个既定交路循环套跑完成1 600 个任务。所产生的初始解是可行的，虽然不一定是最优解，但这将大大降低算法规模，提高求解速度，增加编制动车组运用计划的效率，具有较好的可操作性。

按照以下步骤进行初始可行解的构造：①所有动车组指派空路径；②设U为所有没有安排的任务的集合，u为任务数量；③初始化动车组配属数量Nk，初始化动车组运用周期T，得到班组数n=Nk/T；④将U等分为n个集合u1，u2，…，uq，…，un，每个集合任务数量为uq/n；⑤从u1，u2，…，uq，…，un里面随机抽取1个任务；⑥将这个任务分别插入u1，u2，…，uq，…，un中能够使目标函数值增加最小的可行插入位置；⑦在原有路径中删除此任务；⑧在规定时间内重复⑤～⑦，以尽量获取较好的初始可行解。则最后产生的u1，u2，…，un即为初始路径集合。

综上所述，设计算法如下。

步骤 1：构造初始可行解。

步骤 2：设定最大移出的任务数pmax，最大迭代次数Itermax，以及当前移出任务数n= 1。

步骤 3：设定当前迭代次数Iter= 1。

步骤 4：如果Iter＜Itermax，根据移出 ( Remove )过程，得到从当前解S中移出n个任务后的部分解S'。

步骤 5：根据插入 ( Re-insertion ) 过程，选择最适合的位置插回S'中，如果得到一个更优解Sbest则令S=Sbest并转到步骤 3；如果没有，则返回当前的解S，Iter=Iter+ 1 转到步骤 6。

步骤 6：如果Iter=Itermax，则令n=n+ 1，如果n=Pmax则输出结果，算法终止；否则转到步骤 3。

算法结束的条件有：①迭代达到最大迭代次数或达到一定时间；②当前解在预期值的范围内；③前面 2 项的组合。可以根据不同的情况选择算法的结束。

5 算例

为了验证该模型算法的有效性，拟采用京沪高速铁路和沪宁高速铁路的给定运行图数据作为研究对象，假定初期 2 条线路并不套跑，后期为了成网考虑，套跑运行，以模拟成网条件。

依据给定的京沪、沪宁高速铁路运行图，京沪高速铁路开行列车 100 对/d，沪宁高速铁路开行列车 78 对/d。运输组织采用本线运输组织模式，动车组采用 CRH2 型动车组。CRH2 型动车组的立即折返时间标准为 24 min，一级检修里程为 4 000 km、作业时间标准为 1.5 h，二级检修里程 30 000 km、作业时间标准4 h，检修修程波动系数为 10%。

运算结果中，运行周期分 8 个班组完成所有任务，每个班组 16 个动车组，运行周期为16 d，运用动车组总数为 128 组。动车组交路片段如图 2 所示。

图2 动车组交路片段

通过分析图 2 可以发现该方案中有线路套跑的车次。例如：G113 是京沪高速铁路的车次，在图 2 的交路中，该动车组在完成了 G113 后又完成了 G7026 和 G7179 的运输任务，而这 2 个车次属于沪宁高速铁路，即 2 条线路套跑，这样的安排会降低空车走行，有利于提高动车组使用效率，同时增加车辆的平均日车公里数。通过与给定运行图进行比较，结果方案中这种成网后的优势体现得较为明显。

为了验证大规模邻域搜索算法的有效性，根据模拟退火算法[8]对初始解进行优化，并将其结果与大规模领域搜索算法的优化结果进行比较，发现大规模邻域搜索算法结果较优，算法结果如表 2 所示。

表2 算法结果比较

6 结束语

研究成网条件下动车组运用计划的优化问题，通过引入时空网络，建立成网条件下动车组运用计划的优化模型。该模型运用网络流的思想，能够更加清晰地描述动车组运用情况。结合大规模邻域搜索算法，提出对周期性的多车场动车组运用问题的求解方法。以京沪、沪宁高速铁路数据为例，验证了该算法的可行性和有效性。比较大规模邻域搜索算法与模拟退火算法的优化结果，认为大规模邻域搜索算法能够较快地获取优化结果，对于高速铁路逐步成网后，编制和优化动车组运用计划具有一定的参考价值。

[1] 赵 鹏，杨 浩，胡安洲. 高速铁路动车组的不固定区段使用问题[J]. 铁道学报，1997，19(2)： 15-19.

[2] 赵 鹏，富井规雄. 动车组运用计划及其编制算法[J]. 铁道学报，2003，25(3)：1-7.

[3] 张才春. 基于均衡性的客运专线动车组运用问题研究[D].北京：北京交通大学，2010.

[4] 李 华，韩宝明，李得伟，等. 动车组运用接续网络优化方法研究[J]. 铁道运输与经济，2012，34(1)：76-79.

[5] 刘 钢，孙晚华，韩学雷. 旅客列车车底运用优化模型及算法[J]. 铁道运输与经济，2004，26(2)：62-64.

[6] 中华人民共和国铁道部. 铁路动车组运用维修规程(暂行)[M]. 北京：中国铁道出版社，2007.

[7] 李妍峰，李 军，高自友. 大规模邻域搜索算法求解时变车辆调度问题[J]. 管理科学学报，2012，15(1)：22-32.

[8] 贾玉芬. 高速铁路动车组周期性运用计划问题研究[D]. 北京：北京交通大学，2011.