多目标优化问题的研究
朱 君 蔡延光 汤雅连 杨 军
多目标优化问题的研究
朱 君 蔡延光 汤雅连 杨 军
(广东工业大学 自动化学院,广州 510006)
针对传统方法求解多目标优化问题的局限性,应用一种新的算法求解。遗传算法从问题解的串集开始搜索,覆盖面大,可以同时处理群体中的多个个体,利于全局择优,减少陷入局部最优的风险,而最小生成树具有过程简单清晰、适用性广泛的特点,结合两者的优点,构造了基于生成树的遗传算法。首先通过加权目标规划法求出最优解,然后通过遗传算法和基于生成树的遗传算法求解,结果表明,对于小规模的多目标优化问题,两种算法都可以求出最优解,在求解时间方面,基于生成树的遗传算法比遗传算法更优越。
多目标优化问题;最小生成树;遗传算法
在现实生活中,某个设计方案只要求某一项目标达到最优,这是单目标优化问题。如果设计方案期望某几项指标均能达到最优值,这样的问题就称为多目标优化设计问题。比如厂家生产某种产品,既要求投入资金少,工人少,降低成本,又要工作效率高,利润高,这就是一个多目标优化问题。现实生活中,多目标优化问题[1]中的各个子目标一般是相互矛盾的,也就是同时使所有子目标都达到最优是不可能的,最终目标是尽最大可能达到最优化,它的解并不是唯一的,而是由多个最优解组成的满意解,集合中的各个元素称为Pareto最优解或非劣最优解。由于该问题模型在现实生活中普遍存在,所以本文研究的多目标优化问题具有实际应用意义。
目前,多目标优化问题也得到了广泛的研究。谢涛等人[2]介绍了基于Pareto最优概念的多目标演化算法中的主要技术和理论结果,详细介绍了基于偏好的个体排序、适应值赋值及共享函数等。王跃宣等人[3]考虑了对约束条件的处理问题,提出了求解带约束的多目标优化遗传算法,利用邻域比较与存档操作遗传算法处理多个相互冲突的目标的优化;马瑞等人[4]提出了解决多目标优化问题的新方法和综合考虑水火协调及能源、环境和经济等多目标优化的分组分段电力市场竞标新模型,结果表明了算法的正确性和模型的有效性;李宁等人[5]提出了一种新的基于粒子群的多目标优化算法,用搜索过程中所发现非劣解的一部分构成精英集,通过小生境技术和部分变异的方法提高非劣解集的多样性和分散性;张丽霞等人[6]应用多目标决策理论求解网络计划的多目标优化模型;王晓鹏[7]在自适应遗传算法的基础上引入群体排序技术、小生境技术和Pareto解集过滤器,建立了适用于多目标优化设计的Pareto遗传算法,设计表明Pareto遗传算法是十分有效的。
1 多目标优化问题描述
多目标优化问题[8]起源于许多实际复杂系统的设计、建模和规划问题,包括工业制造、城市运输、森林管理、产品制造、城市布局、网络布局等。几乎每个重要的现实决策问题都要考虑不同约束和处理若干相互冲突的子目标。多目标优化问题可以表达成下面的形式,如式(1)和(2)所示。
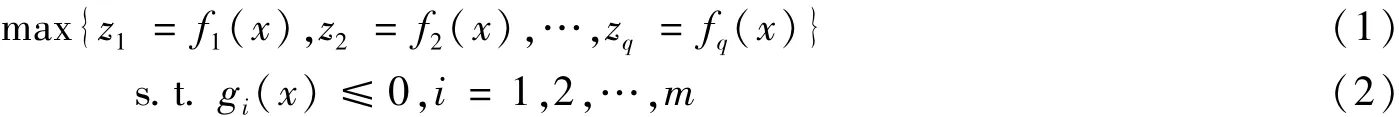
2 两种求解MOP的方法
2.1 加权目标规划
现实的决策环境中各个目标的重要程度是不可能完全一致的,决策者可以判断分析各个目标的重要性,而且子目标在总目标中也占不同的重要程度,可以通过加权系数进行目标规划求解。加权系数是达成函数中各目标偏差变量的系数。加权系数是一种可以用数量来衡量的指标,对属于同一优先等级的不同目标可按其重要程度分别给予不同的加权系数来反映各
加权目标规划的数学模型如下,式(3)为目标函数,式(4)为约束条件。
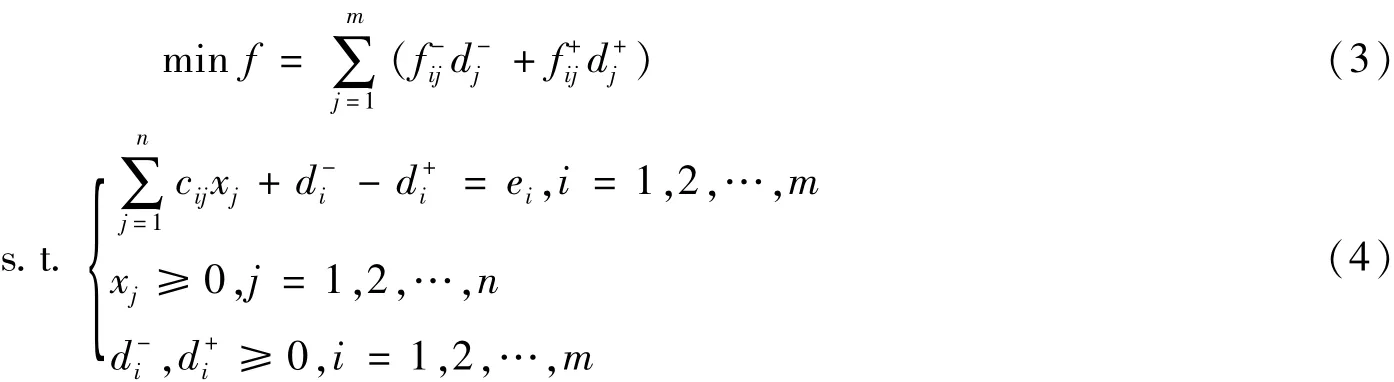
2.2 基于生成树的遗传算法
遗传算法的基本特点是多方向和全局搜索,带有潜在解的种群能够一代代地维持下来。最小生成树问题(minimim spanning tree problem)由Boruvka[8]于1926年首次提出,此后,最小生成树问题被广泛应用于许多组合优化问题中。
最小生成树问题中,考虑连通图C=(V,E),其中V={v1,v2,…,vn}是顶点的有效集合,E={e1,e2,…,em}是边的有限集合。边将顶点之间连接起来。每个边有一个正实数权重W={w1,w2,…,wm}表示距离或费用。最小生成树问题就是寻找图C中连接所有顶点的具有最小权重的子图。
Pareto解集的求解过程
1)设置迭代标志k=1,当前迭代世代t产生的Pareto解集E(t)={φ};
2)若k>i-size,停止;否则,执行3);
3)评价染色体Ak,得到解Fk=[f1(Ak)f2(Ak)…fQ(Ak)],将其与E中所有Pareto解比较;
(i):若任何Pareto优于它,执行4);
(ii):若它优于部分Pareto解,则用它代替E中较差的解;
(iii):若它是新解,则加入E中。
4):k=k+1,返回2)。
整个算法的伪代码如下:
procedure:st-GA/mtp
begin
t←0;
初始化P(t);
计算P(t)的目标函数值;
确定Pareto解集E(t);
计算P(t)的适应值
while不满足终止条件do
begin
对P(t)进行杂交和变异,得到C(t);
更新Pareto解集E(t);
计算C(t)的目标函数值;
更新Pareto解集E(t);
计算C(t)的适应值;
从C(t)中选择P(t+1);
t←t+1;
end
end
3 仿真分析
某工厂准备开发3种产品,重点是确定3种产品的生产计划,并尽量达成目标。总利润不低于120万元,3种产品的单位利润分别为元8、9元和2元;有50名工人,每生产3种产品各1万件分别需要的工人数量为6、1和5名;总投资资金不超过60万元,且生产3种产品需要投入成本2、9和6元。各目标的惩罚权重和各产品的单位贡献如表1和表2所示。

表1 各目标的惩罚权
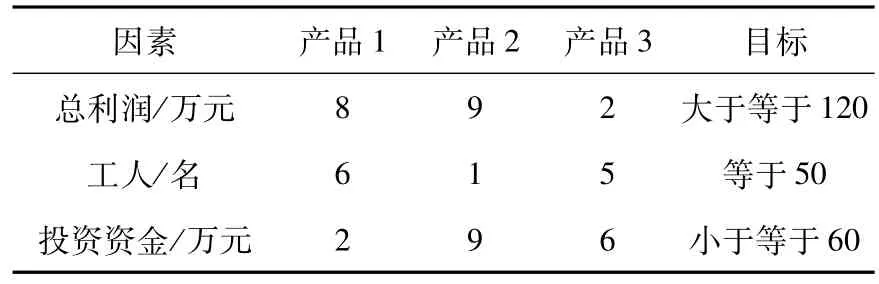
表2 各产品的单位贡献
3.1 加权目标规划法求解MOP
建立数学模型
1)决策变量
产品i的产量xi(i=1,2,3);
正偏差变量d+i、负偏差变量d-i(i=1,2,3)
2)目标函数
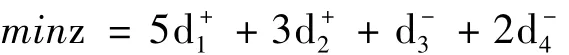
3)约束条件
求解结果:应用Matlab求解界面如图1所示。生产产品1、2和3的数量分别为71739件、69565件和0件。除了第3个目标,其他2个目标都能达成,获得利润120万元,需要工人50人,投入资金76.96万元。
3.2 应用两种算法求解MOP
st-GA的参数设置:初始种群pop-size=30,交叉概率pc=0.8,变异概率pm=0.02,最大迭代次数max gen=1 000,运行30次。
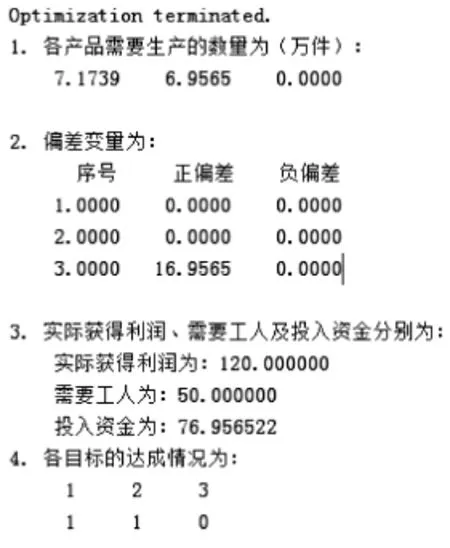
图1 应用Matlab求解界面
GA的参数设置:初始种群pop-size=30,交叉概率pc=0.8,变异概率pm=0.02,最大迭代次数max gen=1 000,运行30次。
在Intel(R)CoreTMi3 CPU 2.53GHz、内存为2.0 G、安装系统为win7的PC机上采用Matlab R2010b编程实现。

表3 GA和st-GA求解MOP的结果
求解结果:由表3可知,通过两种算法都可以求得满意解,但是st-GA比GA消耗更少的时间就可以找到最优解,所以,针对多目标优化问题,st-GA更适用。
4 结语
本文应用一种新的算法求解多目标优化问题。由于遗传算法从问题解的串集开始搜索,覆盖面大,可以同时处理群体中的多个个体,利于全局择优,减少陷入局部最优的风险,而最小生成树具有过程简单清晰、适用性广泛的特点,构造了基于生成树的遗传算法。结果表明,对于小规模的多目标优化问题,虽然两种算法都可以求出最优解,但在求解时间方面,基于生成树的遗传算法比遗传算法更优越,应用改进的算法求解大规模的多目标优化问题是下一步要研究的内容。
[1] 肖晓伟,肖迪,林锦国,等.多目标优化问题的研究概述倡[J].计算机应用研究,2011,28(3):805-809.
[2] 谢涛,陈火旺,康立山.多目标优化的演化算法[J].计算机学报,2003,26(8):997-1003.
[3] 王跃宣,刘连臣,牟盛静,等.处理带约束的多目标优化进化算法[J].清华大学学报:自然科学版,2005,45(1):103-106.
[4] 马瑞,贺仁睦,颜宏文,等.考虑水火协调的多目标优化分组分段竞标模型[J].中国电机工程学报,2004,24(11):53-57.
[5] 李宁,邹彤,孙德宝.基于粒子群的多目标优化算法[J].计算机工程与应用,2005,41(23):43-46.
[6] 张丽霞,侍克斌.施工网络进度计划的多目标优化[J].系统工程理论与实践,2003,23(1):56-61.
[7] 王晓鹏.多目标优化设计中的Pareto遗传算法[J].系统工程与电子技术,2003,25(12):1558-1561.
[8] 玄光男,程润伟.遗传算法与工程优化[M].北京:清华大学出版社,2003.
Research on Multi objective Optimization Problem
ZHU Jun CA IYan-guang TANG Ya-lian YANG Jun
(School of Automation,Guangdong University of Technology,Guangzhou 510006,China)
Aiming at the limitation of the traditional methods to solve the multi-objective optimization problem,this paper applies a new kind of algorithm to it.Genetic Algorithm(GA)starts to search from the set of solution with its big coverage able to handle more than one individual at the same time,beneficial to global optimization,reducing the risk of fall intolocal optimum,while the minimum spanning tree has the characteristics of simple process and wide applicability.Combined with the advantages of the both algorithms,genetic algorithm is constructed on the basis of spanning tree.By finding the optimal solution by weighted goal programming method,and then solving the problem by the genetic algorithm and genetic algorithm based on spanning tree,the result shows that for small-scale multi-objective optimization problem,two algorithms can find out the optimal solution,and interms of solving time,genetic algorithm based on spanning tree is superior to genetic algorithm.
multi objective optimization;minimum spanning tree;genetic algorithm
TP2
A
1009-0312(2014)03-0046-04
2013-12-04
国家自然科学基金(61074147;61074185);广东省自然科学基金(S2011010005059;8351009001000002);广东省教育部产学研结合项目(2012B091000171;2011B090400460);广东省科技计划项目(2012B050600028;2010B090301042)。
朱君(1991—),男,江西新余人,硕士生,主要从事组合优化、物流信息技术与应用方向研究。

