时标上的变时滞二维动力系统的振动性
余晋昌 邓立虎
(1.东莞理工学院 计算机学院,广东东莞 523808;2.东莞理工学院 学报编辑部,广东东莞 523808)
时标上的变时滞二维动力系统的振动性
余晋昌1邓立虎2
(1.东莞理工学院 计算机学院,广东东莞 523808;2.东莞理工学院 学报编辑部,广东东莞 523808)
利用广义Riccati变换和不等式技巧,讨论一类时标上具有两个变时滞的二维动力系统的解的振动性质,得到的振动定理既适用于变时滞二维动力系统,也适用于变时滞二维微分系统和差分系统及某些二阶时滞动力系统。
二维;时滞;动态系统;振动;时标
1988年,德国人Stefan Hilger教授在他的博士论文[1]中首次提出了测度链理论,有三个主要目的:统一,推广和离散化。一个时标(Time Scales)是指实数集的一个非空闭子集,通常用字母T表示,它具有由R诱导的拓朴和R中的顺序关系。在T上定义了前跳算子σ(t):=inf{s∈T:s>t}和后跳算子ρ(t):=sup{s∈T:s<t}。对于函数f:T→R,如果
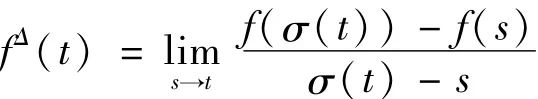
存在(此处fΔ(t)要求t∈Tk:=T{m},其中m为T的最大孤立点,)我们就说fΔ(t)是函数f(t)在t∈T处的Δ-微分。即对任意的ε>0,存在U=(t-δ,t+δ)∩T,使得对所有的s∈U,有
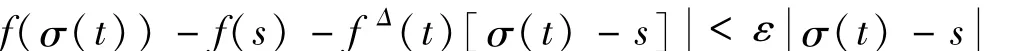
成立。f的Δ-微分与其步差算子μ(t)=σ(t)-t之间有fσ=f+μfΔ,其中fσ=f◦σ。对任意两个Δ -可微函数f和g,它们的积和商Δ-微分分别为

当a,b∈T,f,g∈Crd时,有

及

有关时标理论的论著,这里建议读者参见文献[2]。研究时标理论,既是数学理论本身发展的需要,也是实际问题的需要。由于实际问题所对应的时标动态方程可解决把停止——开始行动和连续行动结合在一起的问题,因此计算机网络、生态学、工程技术、物理学等领域的许多问题用时标动态方程来描述更能揭示其本质属性。例如,利用这一理论建立的昆虫种群模型和电网模型更加切合实际[2-3]。
本文讨论时标T上的二维变时滞动力系统:

的解的振动性质。
总假定系统(1)中的系数及时滞满足下列条件:

(A3)f,g∈C(R,R)是单调不减函数,且对u≠0,有uf(u)>0,ug(u)>0.
本文总假定t0∈T,h1(t0),h2(t0)∈T,记[t0,∞)T:=[t0,∞)∩T。
为了方便,定义

称实值函数组(x(t),y(t))为系统(1)的一个解,如果x,y∈[t0,∞)T,R)且在[t0,∞)T上满足系统(1)。而这里感兴趣的是系统(1)在区间[tx,∞)T(tx≥t0)上满足条件sup{x(t)+ y(t):t>tx}>0的解。习惯上,定义在区间[T0,∞)上的实值连续函数称为是振动的,如果它有任意大的零点,否则称它是非振动的。系统(1)的解称为是振动的,如果它的两个分量x(t),y(t)都是振动的,否则称它是非振动的。系统(1)称为是振动的,如果它的每个解都是振动的。
当T=R时,
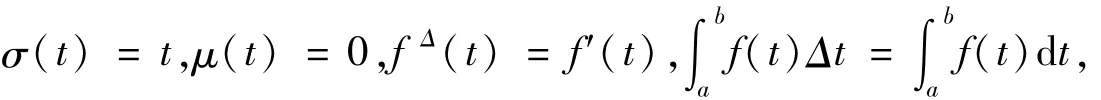
这时,系统(1)为二维时滞微分系统:
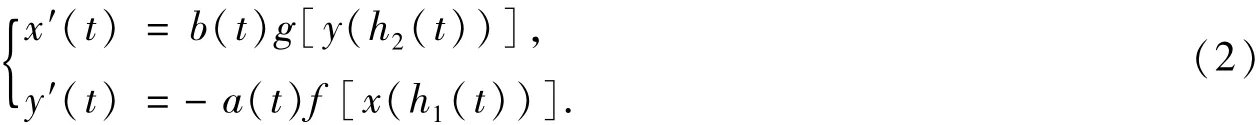
当h1(t)=h2(t)=t时,系统(2)为二维微分系统:

系统(2)及(2')的解的振动性的有关结果可参见文献[4-6]。当T=N且{an}及{bn}为非负序列时,我们有

这时,系统(1)为二维时滞差分系统:
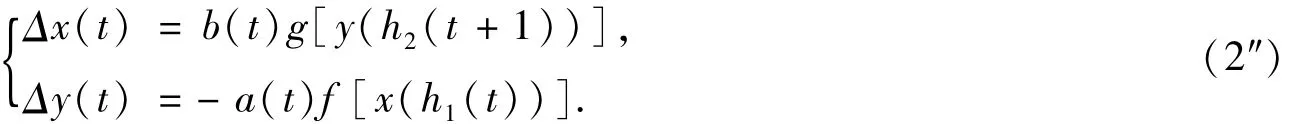
这时,系统(1)为二维时滞差分系统,有关二维差分系统的解的振动性有关结果参见文献[7-8]。
当T=h N:={hk:k∈N,h>0),有

这时,系统(1)为二维时滞步差系统:

当T=qN0:={t:t=qn,n∈N0,q>1),有

这时,系统(1)为二维时滞步差系统:

另外,当系统(1)中系数a(t)在[t0,∞)T上为正,且对任意的u∈R,有f(u)=u时,系统(1)变成二阶时滞动态方程:
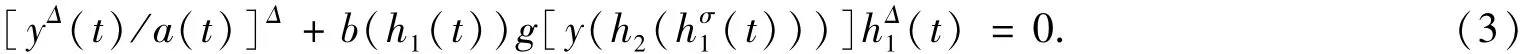
文献[9]讨论了时标上的二维动态系统的振动性,得到了时标上的二维动态系统振动的若干准则,本文借助文献[9]的方法,讨论时标上的变时滞二维动态系统(1)的振动性,我们得到的振动准则既适用于变时滞二维动态系统,也适用于变时滞二维微分系统和差分系统及某些二阶时滞动态方程。有关时标上的动力系统的振动性的最新结果,可参见文献[10-15]。
1 引理
主要结果的证明要用到下面的两个引理,叙述如下:
引理1 假定(A1)~(A3)成立,又设(x(t),y(t))是系统(1)的一个非振动解,那么分量x(t)是非振动的,且分量x(t)与y(t)最终同号。
证明 设(x(t),y(t))是系统(1)的一个解,且分量x(t)是振动的,而分量y(t)是非振动的。不失一般性,设在[t0,∞)T上有y(t)>0,由系统(1)的第一个方程及假设(A2),在[t0,∞)T上,有xΔ(t)≥0。因此,对充分大的t,有x(t)>0或x(t)<0,这将导致矛盾。因此,分量x(t)与y(t)有相同的振动性。
设(x(t),y(t))是系统(1)的一个非振动解,且在[t0,∞)T上分量x(t)>0,x(h1(t))>0。那么,由系统(1)的第二个方程,得到在[t0,∞)T上有yΔ(t)≤0。因此,对t≥t0,有两种情形:y(t)>0或y(t)<0。如果后一种情形成立,由(1)可知,yΔ(t)≤0且xΔ(t)≤0。注意到y(hσ2((t))≤y(h2(t))且g是单调不减的,我们有

这就导致了矛盾。同理可证,分量x(t)<0可推出y(t)<0,对t≥t0。引理1证完。
引理2 假定q:T→R在时标T是Δ-可微的,p∈C1(R,R)。那么p°q:T→R也是Δ-可微的,且有

引理2的证明参见文献[2]。
2 主要结果及证明
这一节,我们来建立系统(1)的振动准则,有
定理1 假定条件(A1)~(A3)成立,又设f,g∈C1(R,R)且满足

则系统(1)在[t0,∞)T上是振动的。
证明(反证法) 设(x(t),y(t))(t≥t0)是系统(1)的一个非振动解。不失一般性,由引理1,我们可设x(t)>0,x(h1(t))>0及y(t)>0,y(h2(t))>0,y(hσ2(t))>0,(t≥t0)。定义

对(8)式微分,由系统(1),引理2及条件(i)(ii),有
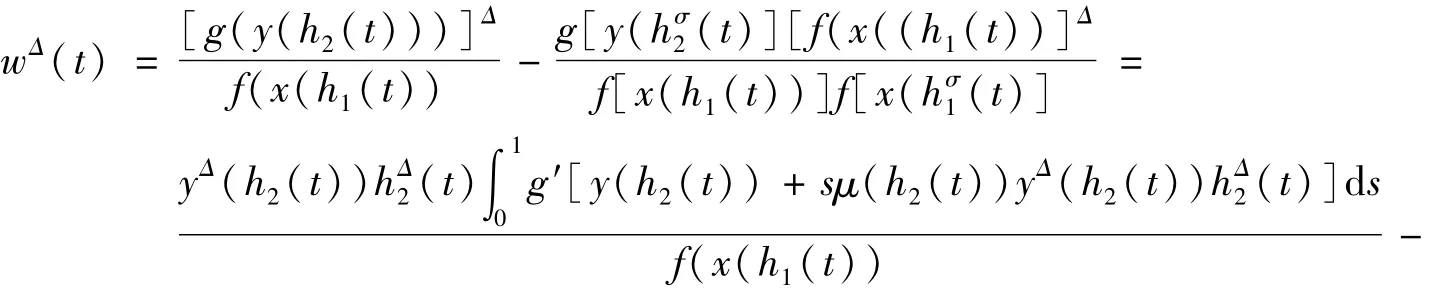

在上面不等式的两边同乘B(t)hΔ1(t),再从t0到t积分,由分部积分公式(参见文献[2]),有

事实上,由系统(1)的第一个方程及(8),有

由于f(x),x(t)是单调不减的,有
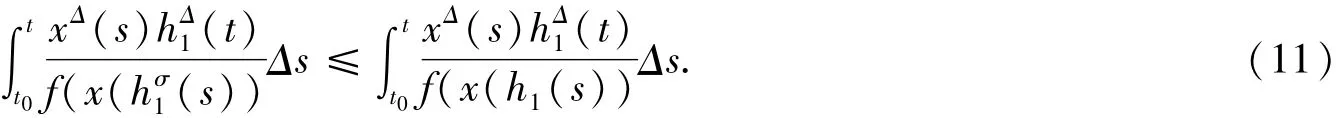
由(10)与(11)式及条件(iii),有
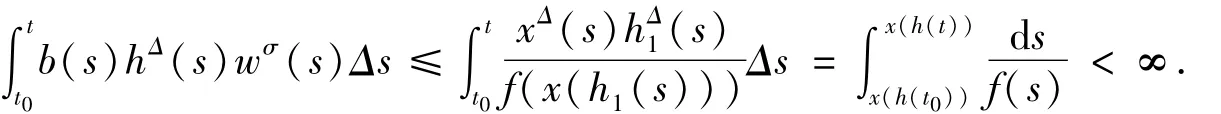
定理2 假定条件(A1)~(A3)成立,又设f,g∈C(R,R)满足
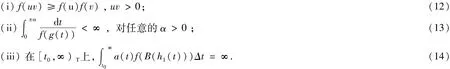
则系统(1)在[t0,∞)T上是振动的。
证明(反证法) 设(x(t),y(t))(t≥t0)是系统(1)的一个非振动解。不失一般性,由引理1,可设x(t)>0,x(h1(t))>0及y(t)>0,y(h2(t))>0,y(hσ2(t))>0,(t≥t0)。由系统(1)可知,xΔ(t)≥0,yΔ(t)≤0,t≥t0。因而存在且有限。对系统(1)的第一个方程从t0到σ(t)上积分得
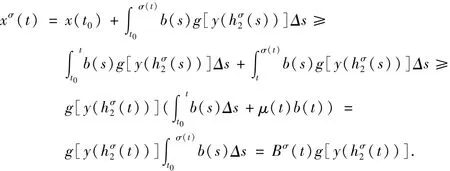
因此,有

由条件(i)及(15)式,得

再由系统(1)的第二个方程,有
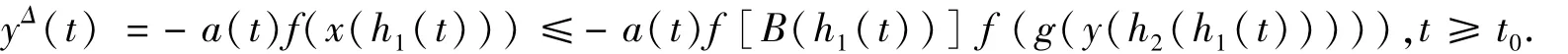
从而

由上式,再根据y(t)单调不增及f,g单调不减,有
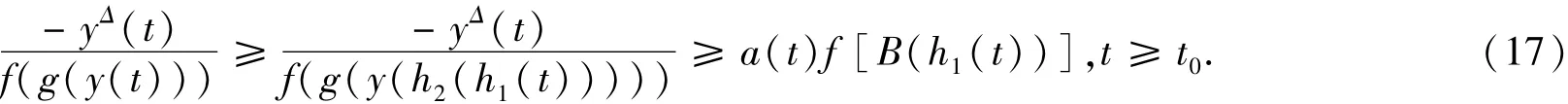
由条件(iii)中的(14)式及(17)式,得

上式与条件(ii)中的(13)相矛盾。定理2证完。
定理3 假定条件(A1)~(A3)成立,又设f,g∈C(R,R)且满足
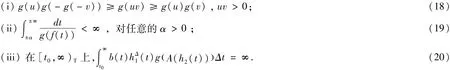
则系统(1)在[t0,∞)T上是振动的。
证明(反证法) 设(x(t),y(t))(t≥t0)是系统(1)的一个非振动解。不失一般性,由引理1,可设x(t)>0,x(h1(t))>0及y(t)>0,y(h2(t))>0,y(t))>0,(t≥t0)。由系统(1)可知,xΔ(t)≥0,yΔ(t)≤0,t≥t0。因而有≥0存在且有限。对系统(1)的第二个方程从σ(t)到∞上积分得

由(18)及(21)式,有

上式从t1(t1≥t0)到t积分,由条件(iii),有
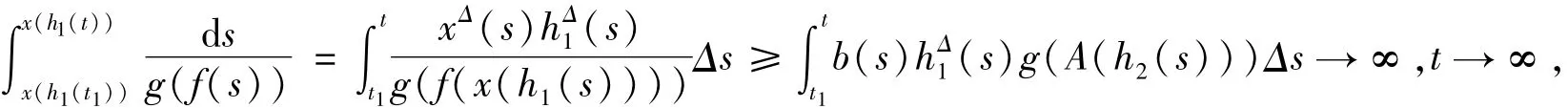
上式与条件(ii)中的(19)相矛盾。定理3证完。
定理4 假定条件(A1)~(A3)成立,又设f,g∈C(R,R)且满足
(i)A(t)<∞,t∈[t0,∞)T;
(ii)在[t0,∞)T上,对于正常数k,有
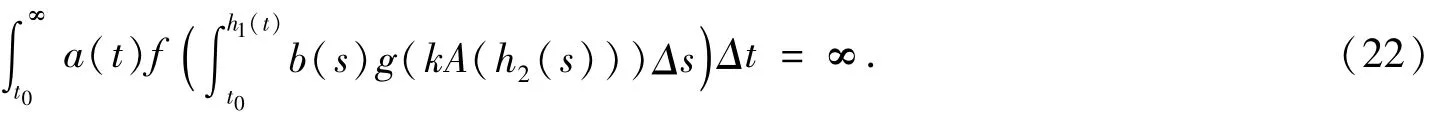
则系统(1)在[t0,∞)T上是振动的。
证明(反证法) 设(x(t),y(t))(t≥t0)是系统(1)的一个非振动解。不失一般性,由引理1,我们可设x(t)>0,x(h1(t))>0及y(t)>0,y(h2(t))>0,y(t))>0,(t≥t0)。由系统(1)可知,xΔ(t)≥0,yΔ(t)≤0,t≥t0.因而有=α≥0。对系统(1)的第二个方程从σ(t)到s上积分得

上式中令s→∞,有

再由(23)式及系统(1)的第一个方程,有
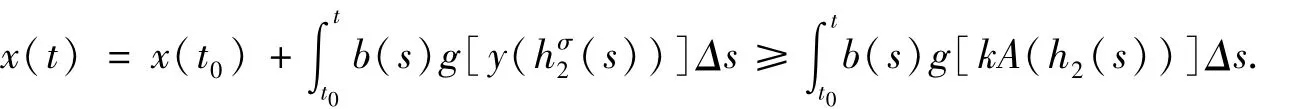
于是,
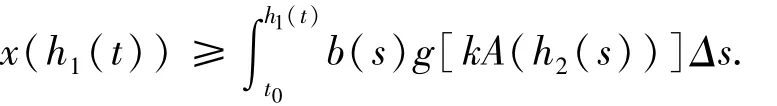
因此,
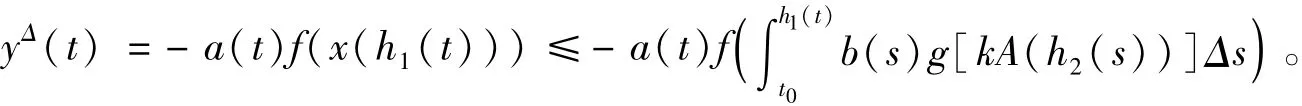
上式从t0到t积分,由条件(ii),有
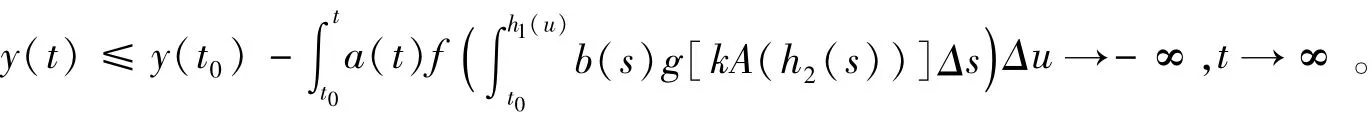
这与y(t)>0,(t≥t0)相矛盾。定理4证完。
由定理1~4,可以得到二维时滞微分系统与差分系统的振动准则,这里不再赘述。
作为例子,考虑下面的时滞动态系统
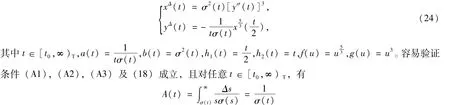
存在,及

另外,

即条件(19)及(20)成立。因此,由定理3知,系统(24)是振动的。
[1] Hilger S.Analysis on measure chains—a unified approach to continuous and discrete calculus[J].Results Math,1990(19):18-51.
[2] Bohner M,Peterson A.Dynamic Eruation on Time Scales:An Introduction with Application[M].Birkhauser:Boston,2001.
[3] Agarwal R P,Bohner M,O’Regan D.Dynamic eruation ontime scales:A survey[J].JComput Math Appl,2002(141):1-26.
[4] Kordonis I-G E,Philos Ch G.Onthe oscillation of nonlinear two-dimensional differential systems[J].Proc Amer Math Soc,1998(126):1661 -1667.
[5] Kwong M K,Wong JSW.Oscillation of Emden-Fowler systems[J].Differential Integral Eruations,1998(2):133-141.
[6] Yu JC.Oscillationtheorems for a class of two-dimensional delay differential systems[J].Ann Of Diff Ers,2013,29(1):107-113.
[7] Jiang J,Tang X.Oscillation and asymptotic behavior of two-dimensional difference systems[J].JComput Math Appl,2007(54):1240-1249.
[8] Jiang J,Li X.Oscillation and non-oscillation of two-dimensional difference systems[J].JComput Math Appl,2006(188):77-88.
[9] Xu Y,Xu Z T.Oscillation criteria for two-dimensional dynamic systems ontime scales[J].JComput Math Appl,2009(225):9-19.
[10] Sahiner Y.Oscillation of second order delay differential equations ontime scales[J].Nonlinear Anal,2005(63):1073-1080.
[11] Zhang B G,Zhu S.Oscillation of second-order nonlinear delay dynamic equations ontime scales[J].ComputMath Appl,2005(49):599-609.
[12] Wang B,Xu Z T.Oscillation of second order neutral Emder-Fowler delay dynamic equations of mixed type[J].Dynamic Systems and Applications,2009(18):441-456.
[13] Huang X C,Xu Z T.Kamenev-type and interval oscillationtheorems for second order nonlinear delay dynamic equations[J].Dynamic Systems and Applications,2009(18):571-588.
[14] Saker SH.Oscillation of nonlinear dynamic equations ontime scales[J].Appl Math Comput,2004(148):81-91.
[15] Saker SH.Oscillation of second order neutral delay nonlinear dynamic equations ontime scales[J].JComput ApplMath,2006(187):123 -141.
The Oscillation of Two-DimensionalDelay Dynamic Systems on Time Scales
YU Jin-c hang1DENG Li-hu2
(1.Computer College,Dongguan University of Technology,Dongguan 523808,China;
2.Editorial Department of Journal,Dongguan University of Technology,Dongguan 523808,China)
By the use of generalized Riccati transformation and ineruality technirue,this paper studies the oscillation of two-dimensional delay dynamic systems on time scales.Our results not only unify the oscillation of two-dimensional delay differential systems on time scales,but also include the oscillation results for delay differential systems,providing new oscillation criteria for delay difference systems.
two-dimensional;delay;dynamic systems;oscillation;time scales 2000
34K11;34CK10;39A10;34B10
O175
符:A
1009-0312(2014)03-0001-07
2014-02-19
余晋昌(1964—),男,广东大埔人,副教授,主要从事泛函微分方程研究。
MR(2000)主题分类:34C10;34K11;35B10;39A10

