无位置传感器控制的双电机驱动系统性能研究
田俊英
(菏泽学院 蒋震机电工程学院,菏泽 274015)
0 引言
随着现代工业的发展,高性能的调速系统被应用到多电机特别是双电机驱动系统中[1~5]。这些系统由于其灵活性、可靠性以及方便安装的优点被应用到大功率场合下。但是这些系统包含了大量昂贵且体积庞大的功率开关器件,因此,单逆变器驱动双电机系统成为现代工业和牵引应用上的优选方案。
如今已存在很多成熟的技术被应用到高性能电机控制中。给出共直流侧电压的双逆变器驱动双电机控制方案[6];一些文献提出了单逆变器驱动双电机的方案[7~9];论证了四桥臂逆变器驱动双电机的方案[10];有些文献提出五桥臂逆变器驱动双电机系统的控制档案[2,15]。但是这些方案都没有将无速度传感器技术应用到控制方案中。
无速度传感器技术的应用将大大提高系统的机械鲁棒性,也有效的降低了产品的成本。因此,很多学者致力于将无位置传感器技术应用到矢量控制中。其中一部分方案是先估计出电机转速再计算转自位置用于矢量控制[16],还有一部分是直接根据状态方程估计出电机转子位置用于矢量控制[17]。电机转子位置估计方案法主要有扩展卡尔曼滤波算法(EKF)以及模型参考自适应算法(MRAS)等。
在这些方案中,MRAS以其实施简单、系统稳定以及不需要任何额外的已知参数和算法空间的优点被广泛接受。MRAS需引入两个模型(参考模型和可调模型),这两个模型有相同的输入量,通过处理它们的输出误差来辨识未知参数(这里是转子角速度)。
本文引入基于MRAS的无位置传感器技术来估计电机“A”和“B”的转子角速度。系统框图如图1所示。

图1 系统功能框图
1 五桥臂逆变器(FLI)
五桥臂逆变器(FLI)包括十个开关器件,其中一个桥臂被双电机共享,如图2所示。由图中可以看出,第三个桥臂同时连接到A电机的c相和B电机的c相。直流侧母线电压dcv取电机的额定电压值[13]。

图2 五桥臂逆变器(FLI)供电双PMSMs示意图
2 调制技术
使用空间矢量脉宽调制技术(SVPWM)[14],SVPWM原理简单,在单核处理器中容易实现,可以为五桥臂逆变器(FLI)提供标准的三相调制波。

图3 单逆变器双电机系统空间矢量脉宽调制技术(SVPWMs)
图3显示了单逆变器双电机系统下的SVPWMs配置方式,采用了一种特殊的方法将SVPWM信号从六路整合成五路,依据如式(1)。
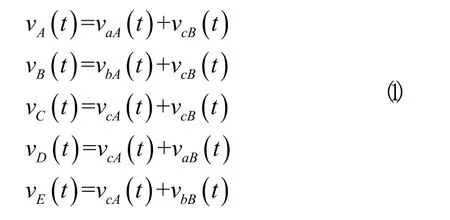
式中“A”和“B”分别代表永磁同步电机A(PMSM A)和B(PMSM B),从式(1)中可以看出, vcB(t)信号被加载到A电机的每一相中,相当于零序分量,在线电压中将被抵消掉,所以vcB(t)对A电机的影响可以忽略。同理可以得出vcA(t)对B电机的影响可以被忽略。
3 永磁同步电机(PMSM)数学模型
电机A(PMSM A)在d-q坐标系下的数学模型可以被描述为如下公式。

式中, vd、 vq表示d-q轴电压,id、iq表示轴电流, we表示电角速度, rs表示定子每相绕线电阻,yd、 yq表示磁场通过d-q轴的磁链。
yd、 yq可被表达成如下式:

式中,ym表示永磁体产生的磁链, Ld、 Lq表示d-q电感。
将(3)式带入(2)式,可的电机端电压约束方程如下:

电机电磁转矩方程如下:

同电机A一样,将式(2)~(5)的下标“A”换成“B”即得电机B的数学模型。
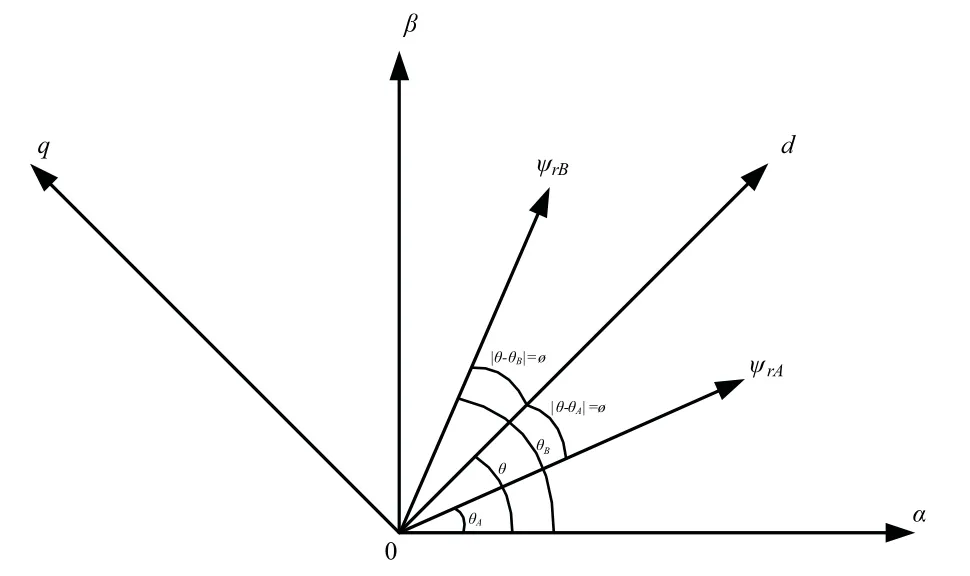
图4 双电机系统d-q坐标系
其中, yrA、 yrB代表电机A和B的磁链矢量,qA、 qB代表转子位置。
由图4可知,电机A和B的电磁转矩表达式如下:
以d轴作为参考轴,定子电流空间矢量可以表示为:

设转子永磁体磁链大小不变,由电磁转矩公式知,通过改变定子电流的相位以及幅值可以改变电磁转矩的大小。
4 基于模型参考自适应的转速估计
图5所示为基于模型参考自适应的转速估计结构框图,包括参考模型、可调模型以及自适应机制三个部分。其设计的目标是确保系统噪声达到最小,以免影响系统性能及稳性定性。

图5 模型参考自适应转速估计功能框图
参考模型中,三相电压及电流被转换到d-q轴电压以及电流。d-q轴电压电流也被用在可调模型以及自适应机构中。从公式(5)知,可将可调模型用下式表达:

参考模型的输出量为参考模型d-q轴电流的估计值,此估计值与实际值作比较用以自适应机构的转速估计。为保证自适应系统的稳定性,可根据Popov超稳定理论得出自适应机制如下:
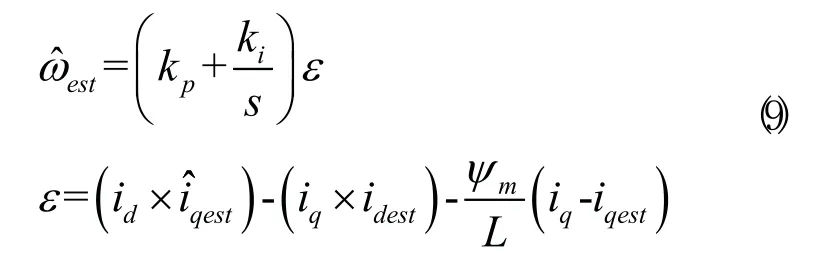
式中,e表示的是估计速度与实际速度在忽略参数对其影响的情况下的误差,此误差可通过PI调节器计算出估计转速。
5 仿真结果
图6至图13所示为是双电机的速度响应情况,电机A和B的相关参数如表3所示,A和B具有相同的参数和规格。其测试和仿真将在如下不同操作环境下进行。

图6 电机A(2000r/m)和单电机B(500r/m)对负载扰动的转速响应

图7 电机A(2000r/m)和单电机B(500r/m)对负载扰动的转速响应(细节放大)
从图6和图7中可以看出电机A在给定转速2000r/m时的实际转速响应情况。在t=0.8s时,电机A的负载转矩从额定负载转矩的25%(2N.m)变化到额定负载转矩的125%(10N.m),同时电机B在给定转速500r/m下保持恒定负载转矩(8N.m)运行。从图中可以看出,系统在宽负载转矩下可保持稳定。
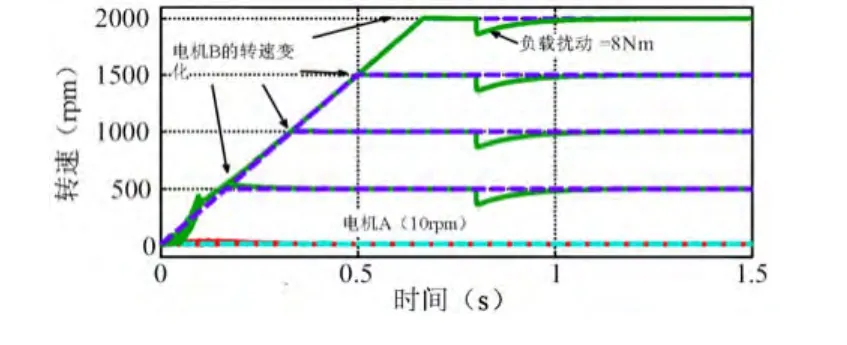
图8 电机B在不同给定转速下对负载转矩变化的响应情况(电机A的转速为10r/m)
图8所示为电机B在有负载扰动的情况下对不同给定转速的速度响应情况,电机A的给定转速为10r/m。电机A在不同转速下的超调量如表1所示。

表1 双电机启动时电机A在不同给定转速下的超调量

图9 电机A和电机B对0转速给定的瞬态响应

图10 电机A和电机B对0转速给定的瞬态响应(细节放大)
图9和图10所示为电机A和电机B在0转速给定下的响应情况。从图中可以看出,在此时的电流情况下,本文所提出的无传感器技术没有任何积分问题,从而为0转速运行提供了依据。

图11 电机A和电机B对反向给定转速(A:-2000r/m;B:-10r/m)的响应
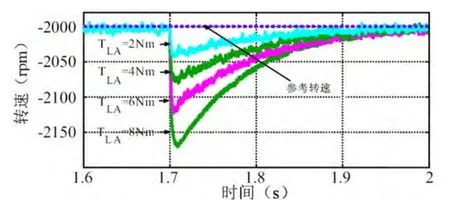
图12 电机A和电机B对反向给定转速
图11和图12所示为电机A在反向运行时的转速响应情况。同时,与正向运行类似,在t=1.7s时实际负载转矩扰动。
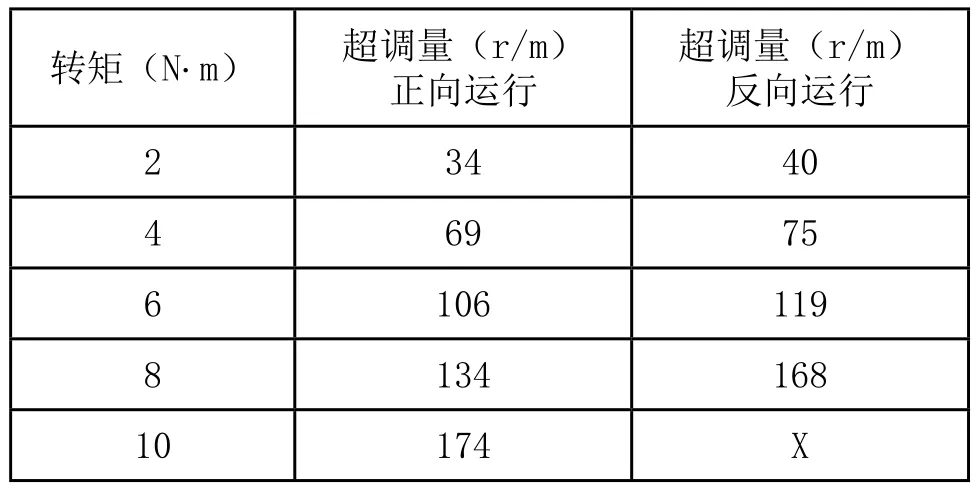
表2 电机A在不同转矩下的转速超调量
表2所示为电机超调量随着负载的增加而增大,同时反向运行的超调量交正向运行稍大。
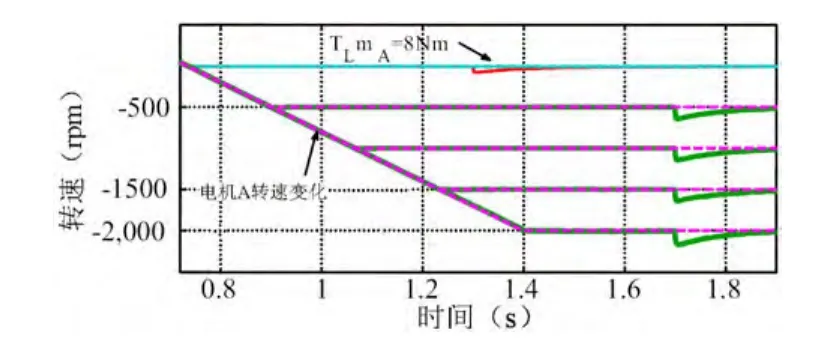
图13 电机A在不同反向给定转速下对负载转矩变化的响应情况,电机B的转速为-10r/m
图13所示为电机A在有负载转矩扰动的情况下对不同给定的反向转速的速度响应情况,电机B给定转速-10r/m。通过观察,可以发现在电机反转的情况下,给定转速从-500r/m到-2000r/m时都没有出现速度超调现象。从而证明本文所提出的方案具有很好的启动特性特别在反转的情况下。

表3 电机A和B各项参数
6 结束语
本文研究基于无位置传感器的单逆变器驱动双电机系统在不同运行条件下的速度特性,电机A和电机B都是永磁同步电机(PMSM)且具有相同的参数。运行条件如下:1) 电机正反转且具有负载扰动;2) 不同给定转速(包括正反转);3) 0转速。仿真结果表明,该系统具有良好地稳态与瞬态特性,与单逆变器单电机系统具有相同的性能。
[1] A.Bouscayrol, B.Francois, P.Delarue,and J.Niiranen."Control implementation of a five-leg AC-AC converter to supply a three-phaseinduction machine[J].Power Electronics,IEEE Transactions 2005(20):107-115.
[2] P.Delarue, A. Bouscayrol, and E. Semail. Generic control method of multileg voltage source converters for fast practical implementation[J].Power Electronics, IEEE Transactions 2003(18):517-526.
[3] C. B. Jacobina,E.C.dos Santos, E. R. C. da Silva, M. B.de Correa, A..M. N. Lima, and T. M. Oliveira. Reduced Switch Count Multiple Three-Phase AC Machine Drive Systems[J].Power Electronics, IEEE Transactions 2008(23):966-967.
[4] M. Jones,S.N.Vukosavic, and E. Levi. Parallel-Connected Multiphase Multidrive Systems With Single Inverter Supply[J].Industrial Electronics,IEEE Transactions 2009(56):2047-2057.
[5] E. Ledezma,B.McGrath, A. Munoz, and T. A. Lipo, "Dual AC-drive system with a reduced switch count[J].Industry Applications,IEEE Transactions 2001(37):1325-1733.
[6] Y.He,Y.Wang, J.Wu,Y.Feng, and J. Liu. A comparative study of space vector PWM strategy for dual three-phase permanent-magnet synchronous motor drives[J].in Applied Power Electronics Conference and Exposition (APEC),2010 Twenty-Fifth: Annual IEEE.2010(25):915-919.
[7] J. M. Lazi, Z.Ibrahim,M.Sulaiman, I. W. Jamaludin, and M. Y. Lada,"Performance comparison of SVPWM and Hysteresis Current Control for Dual motor drives[J].in IEEE International Conference on Power and Energy(PECon),, Kuala Lumpur, Malaysia,2011:75-80.
[8] J. M. Lazi,Z.Ibrahim,M.Sulaiman,I.W.Jamaludin, and M. Y. Lada. Performance comparison of SVPWM and Hysteresis Current Control for Dual motor drives[J].in Applied Power Electronics Colloqium(IAPEC), 2011 IEEE, Johor Baharu,Malaysia,2011:75-80.
[9] Z. I. Jurifa Mat Lazi, Marizan Sulaiman, Fizatul Aini Patakor, Siti Noormiza Mat Isa. Fuzzy Logic Speed Controller with Reduced Rule Base for Dual PMSM Drives[J].International Journal Electrical and Electronic Engineering on World Accademy of Science Engineering and Technology 2011(77)252-257.
[10] E. Ledezma,B.McGrath, A. Munoz, and T. Lipo. Dual AC-drive system with a reduced switch count[J].Industry Applications, IEEE Transactions 2002(37):1325-1333.
[11] P. Delarue,A.Bouscayrol,and B.Francois. Control implementation of a five leg voltage source inverter supplying two three-phase induction machines[J].in IEEE International Conference on Electric Machines and Drives.2003(3):1909-1915.
[12] M. Jones,D.Dujic,and E.Levi. A performance comparison of PWM techniques for five-leg VSIs supplying two-motor drives[A].34th Annual Conference of IEEE on Industrial Electronic 2008,IECON 2008[C].2008:508-513.
[13] M. Jones,S.Vukosavic,D.Dujic, E. Levi,and P.Wright,“Five-leg inverter PWM technique for reduced switch count two-motor constant power applications[C].Electric Power Applications,IET 2008(2):275-287.
[14] K. Oka,Y.Nozawa, and K. Matsuse. Improved method of voltage utility factor for PWM control method of fiveleg inverter[A].The 37th IEEE Conference on Power Electronics Specialists,2006 (PESC'06),Jeju Island,Korea[C].2006:1-5.
[15] S. N.Vukosavic,M. Jones,D.Dujic, and E. Levi. An improved PWMmethod for a five-leg inverter supplying two three-phase motors[A].IEEE Symposium on Industrial Electronics 2008,ISIE 2008[C].2008:160-165.
[16] S.Bolognani,R.Oboe, and M.Zigliotto.Sensorless fulldigital PMSM drive with EKF estimation of speed and rotor position[J].Industrial Electronics,IEEE Transactions 1999(46):184-191.
[17] Z. M.A.Peixo,F.M.Freitas Sa, P.F.Seixas, B.R.Menezes,P.CCortizo,and W.S.Lacerda. Application of sliding mode observer for induced e.m.f., position and speed estimation of permanent magnet motors[A].Power Electronics and Drive Systems,1995., Proceedings of 1995 International Conference[C].1995(2):599-604.
[18] M. Eskola and H. Tuusa. Comparison of MRAS and novel simple method for position estimation in PMSM drives[A].Power Electronics Specialist Conference,2003. PESC'03.2003 IEEE 34th Annual[C].2003(2):550-555.
[19] M.E.Elbuluk, T.Liu,and I.Husain. Neural network based model reference adaptive systems for high performance motor drives and motion controls[J].Industry Applications,IEEE Transactions 2002(38):879-886.
[20] S.Maiti,C.Chakraborty,Y.Hori,and M.C.Ta. Model Reference Adaptive Controller-Based Rotor Resistance and Speed Estimation Techniques for Vector Controlled Induction Motor Drive Utilizing Reactive Power[J].Industrial Electronics,IEEE Transactions 2008(55):594-601.
[21]M.Acampa,A.Del Pizzo,and D.Iannuzzi. Optimized control technique of single inverter dual motor AC-brushless drives[A].Universities Power Engineering Conference,2008,UPEC 2008[C].2008:1-6.

