基于JPDA-MPC的单站纯方位多目标跟踪
邵俊伟,单 奇,吴 超
(中国电子科技集团公司第三十八研究所,安徽 合肥 230088)
0 引言
地面单站静止雷达对目标进行纯方位跟踪时,无法得到目标的全部运动参数[1],但此时仍可估计目标的方位、航向等状态,为目标的自动筛选、威胁评估等决策提供支撑[2]。纯方位跟踪系统是非线性的,坐标系及滤波算法的选择是首先要解决的两个问题。在直角坐标系下建立跟踪模型并进行滤波,结果通常不稳定且容易发散。文献[3]中提出的修正的极坐标系(MPC)下的扩展Kalman滤波方法,可以极小化系统的二阶非线性损失,且当雷达与目标的相对加速度为零时,不可观的距离状态与可观的其他状态能自动解耦,得到稳定和渐近无偏的估计。
由于对目标进行纯方位跟踪时,得到的量测中只有目标的方位信息,因此相比带距离量测的多目标跟踪,此时更易发生关联错误。传统的关联算法,如最近邻标准滤波器[4](NNSF)等,难以稳定地实现纯方位多目标跟踪。联合概率数据关联[5](JPDA)考虑跟踪门内的所有量测与目标关联的可能性,并以等效量测来对目标的状态进行更新,降低了错误关联的可能性,具有较好的多目标相关性能。
本文结合修正的极坐标系下的扩展Kalman滤波算法及JPDA关联算法,来实现对单站多目标的纯方位跟踪,并通过仿真试验对比JPDA-MPC与NNSFMPC方法的跟踪效果,结果表明,前者具有更好的跟踪稳定性和跟踪精度。
1 算法描述
1.1 修正的极坐标系
假定以静止单雷达对目标作纯方位跟踪,其扫描周期为T,目标的方位角为φ,距离为r。在修正的极坐标系中,以φ、和/r为状态变量,即取状态向量为:
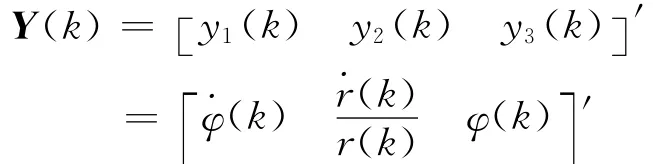
修正极坐标系下的状态方程可以表示为[3]:

量测方程为:
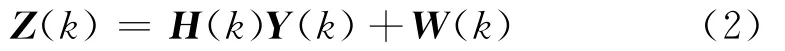
式中,Z(k)是量测值,H(k)是量测矩阵,W(k)是协方差矩阵为R(k)的零均值、白色高斯量测噪声,即:
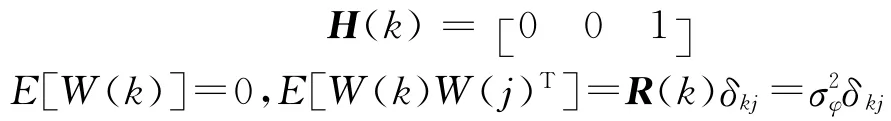
式中δkj为Kronecker delta函数,即k=j时,δkj=1,否则δkj=0。
状态方程(1)是非线性的,本文使用扩展Kalman滤波器(Extended Kalman Filter)[6-7]对其进行滤波,具体过程如下。
1)滤波预测
状态的一步预测为:
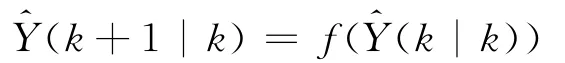
状态预测误差协方差矩阵为:
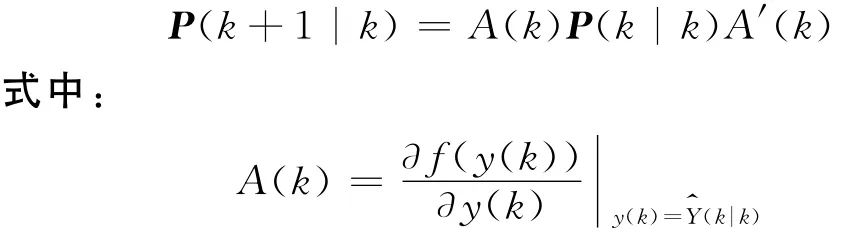
新息协方差矩阵为:
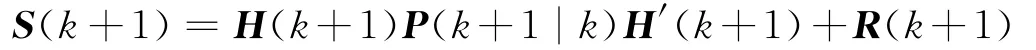
增益矩阵为:
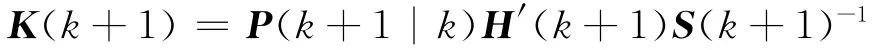
2)滤波更新
状态更新方程为:

协方差更新方程为:

当存在虚警或被跟踪的目标有多个时,还需考虑目标与量测的关联问题。由于对目标进行纯方位跟踪时,得到的量测中只有目标的方位信息,因此相比带距离量测的多目标跟踪,此时更易发生关联错误。本文中使用JPDA算法进行关联,以降低错误关联的可能性,实现稳定的纯方位多目标跟踪。
1.2 JPDA 算法
JPDA考虑跟踪门内的所有量测与目标关联的可能性,并计算概率来对这些量测进行加权,得到的等效量测用来对目标的状态进行更新,是一种性能优越的多目标关联算法。JPDA算法的执行可以分为以下几个步骤[5-7]:
1)构造确认矩阵

2)拆分确认矩阵生成可行矩阵
假定每一个量测有唯一的源,且每个目标最多有一个量测以其为源,在此假设下对确认矩阵进行拆分,得到与可行事件θk,i对应的可行矩阵。
3)由可行矩阵计算关联概率
量测j与目标t关联的概率为:
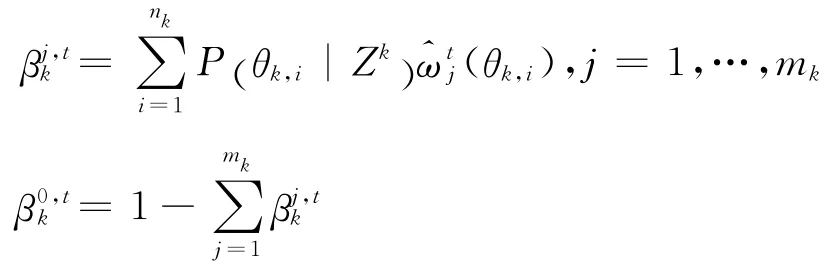
式中(θk,i)表示可行事件θk,i中量测j与目标t是否关联,且为可行事件θk,i的后验概率。
4)由关联概率更新状态和状态误差协方差矩阵
目标t的状态估计为:


式中为对目标t进行EKF滤波时得到的状态预测误差协方差矩阵。
1.3 JPDA-MPC 方法
使用JPDA-MPC方法对目标进行纯方位跟踪的单步关联滤波过程为:
1)EKF滤波预测
使用EKF滤波算法按状态方程计算目标t的状态预测,状态预测误差协方差矩阵,新息协方差矩阵及增益矩阵。
2)生成关联假设
由量测方程(2)计算量测预测,然后根据k+1时刻的量测按JPDA算法构造确认矩阵,并拆分确认矩阵得到关联假设,计算量测j与目标t关联的概率
3)EKF滤波更新
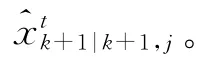
4)组合状态估计
JPDA-MPC的具体流程如图1所示。
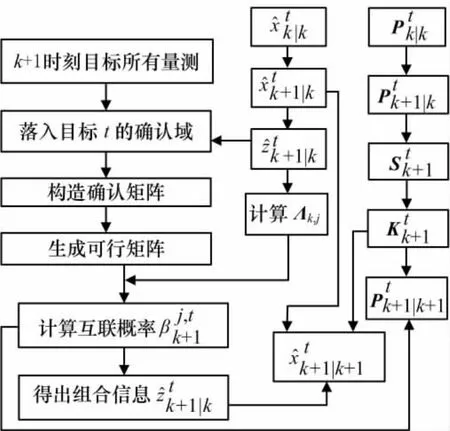
图1 JPDA-MPC单步关联滤波流程图
2 仿真结果及分析
考虑以下运动场景:两目标初始位置分别为(x1,y1)= (131944m,317875m)及 (x2,y2)= (82124m,268055m),且均以277m/s的速度匀速飞行,航向分别为150°和120°(正北为0°),如图2所示。
雷达跟踪过程持续1000s,其扫描周期为T=10s,方位角测量误差为0.3°。方位角的真实值如图3所示。
分别使用JPDA-MPC和NNSF-MPC对目标进行纯方位跟踪,仿真次数100次,跟踪误差均方根(RMS)如图4所示。

图2 目标的真实航迹
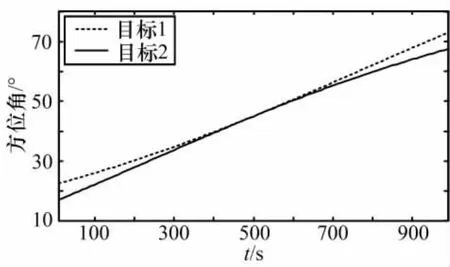
图3 目标的真实方位角
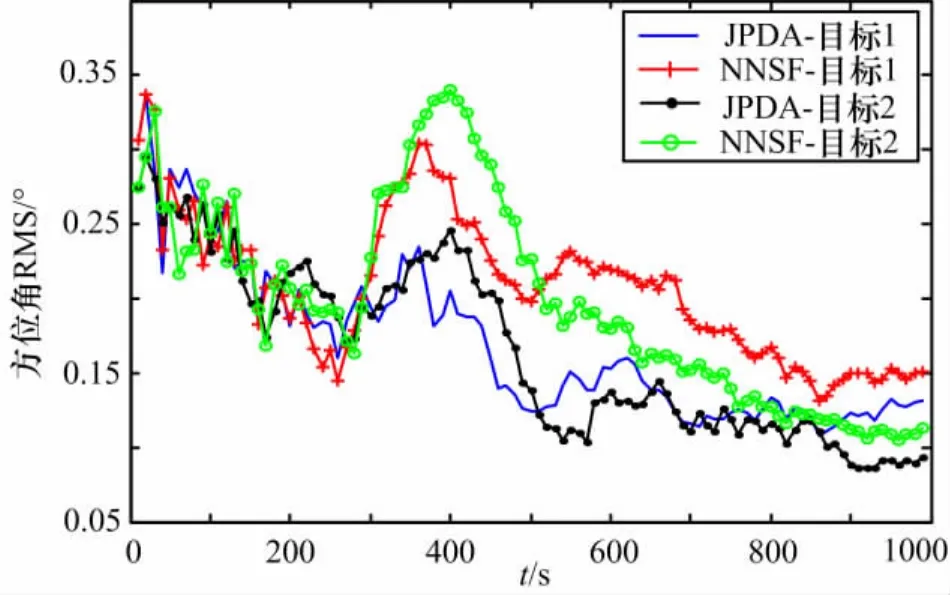
图4 方位角跟踪误差
从图4中可以看出,JPDA-MPC方法具有更好的跟踪精度,且跟踪过程更为稳定。特别是在第30到第70步两目标方位角相差较小的时间段内,NNSF-MPC方法易出现关联错误,甚至会滤波发散。而JPDAMPC方法却没有出现类似问题,这是因为当跟踪门相交时,JPDA-MPC方法会由后验概率计算等效量测位置并进行滤波,虽然等效量测会与真实量测有偏差,但是这种偏差本身较小,并且使用等效量测降低了错误关联的可能性,从而使得JPDA-MPC具有更好的跟踪稳定性和跟踪精度。
3 结束语
本文将修正的极坐标系下的跟踪模型与JPDA关联算法结合,并应用到单站多目标的纯方位跟踪中,克服了纯方位跟踪时由于量测信息有限易导致关联错误的问题。仿真结果表明,与NNSF-MPC方法相比,JPDA-MPC方法具有更好的跟踪稳定性和跟踪精度。
[1]许志刚,盛安冬.二维单站纯方位运动目标跟踪的可观测性[J].兵工学报,2007,28(5):617-620.
[2]张晓勇,罗来源.单静止站纯方位目标航向估计[J].声学技术,2012,31(6):566-569.
[3]Aidala VJ,Hammel SE.Utilization of modified polar coordinates for bearing-only tracking[J].IEEE Trans.on Automatic Control,1983,28(3):283-293.
[4]Singer RA,Sea RG.A new filter for optimal tracking in dense multitarget environment[C]∥Proceedings of the ninth Allerton Conference Circuit and System Theory,Urbana,1971:201-211.
[5]Formann TE,Bar-Shalom Y,Scheffe M.Sonar tracking of multiple targets using joint probabilistic data association[J].IEEE Journal of Oceanic Engineering,1983,8(3):173-183.
[6]韩崇昭,朱洪艳,段战胜.多源信息融合[M].2版.北京:清华大学出版社,2010.
[7]何友,修建娟,张晶炜,等.雷达数据处理[M].2版.北京:电子工业出版社,2009.

