一种基于软件的数据时标修正算法

张鑫波，张 冰

（中国电子科技集团公司第五十四研究所，河北 石家庄 050081）

在测控领域中，测角数据的准确性直接决定着卫星的定轨精度。各测控站在每次任务中直接将打有时标的测角数据上报中心。为便于比对和数据分析，中心要求各测站上报的测角数据时标必须是整点形式（通常取整50ms）。而各测站的整点测角数据，大多是基于Windows中断机制采集保存的。在实际工程中，计算机上运行的各程序软件都会不同程度地采用Windows中断，这样势必会影响测角数据的时标采集，偶尔会出现中断丢失或时标不整点的现象。尽管测角数据是真实的，但不便于中心进行数据比对。因此，笔者试图采用软件修正的办法对数据时标点进行修正，以提高数据的比对效率。

1 软件修正算法

各设备在硬件中断（50ms）中，都会通过时统卡读取时统的系统时间，首先将包含年月日时分秒毫秒的时间转换为毫秒，经过与上一个周期记录的时间进行比对，如果时间差为整50ms，则认为正确时标，否则需要进行时标修正，并利用前几点数据计算出修正后时标对应的数据点。对于算法中用的一些变量，定义如下：

T0：当前的系统时间转化为的毫秒数；

T1：上一个周期系统时间转换为的毫秒数；

Δ：当前时间与上一周期时间毫秒时间差（即：T0－T1）；

bStart：基准时间点选择标志；

M：毫秒时间差包含50ms的个数（即：Δ/50，除法结果的商）；

N：毫秒时间差减去50ms倍数后的余数（即：Δ%50，除法结果的余数）；

A0：当前周期内的角度值；

A1：前一个周期内的角度值；

A2：前两个周期内的角度值。

1.1 基准时间点的选择

算法通过对时间间隔Δ进行比较分析。重要前提，就是上一周期时间点必须是准确的整50ms，否则无法保证后续时间修正的准确性，其程序流程图见图1。程序初始化时各参数变量均为零，第一个判断为了使软件或时统设备在启动正常后进入本流程，第二个判断用于跳出对初始基准时间点的选择，第三个判断是对初始基准时间点T0的选择。

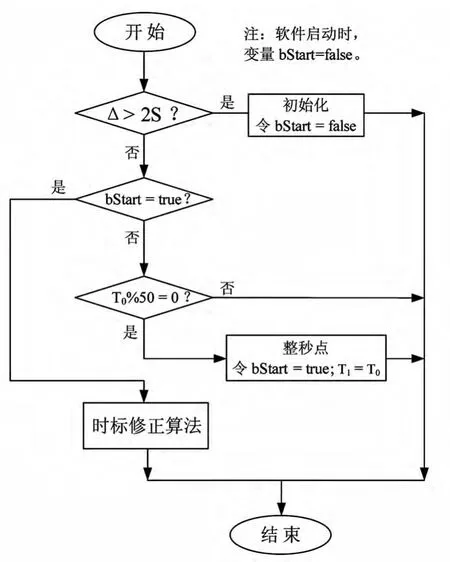
图1 时标基准点选择流程图

1.2 数据递推迭代

根据物理学中的速度相关公式，可以由前两点的速度、距离信息递推出下一点的距离信息。将式（1）～ （4）带入（5）中，可推到得到式（6）。

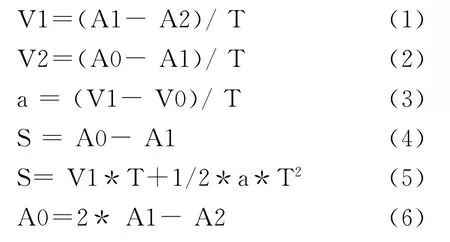
1.3 时标修正算法

经过对大量数据记录文件的分析，发现时标数据的变化主要包含以下4种情况：

1）时间间隔Δ＝0，即连续产生了2次中断，采集到了相同的数据，丢弃本周期内采样数据；

2）时间间隔0＜Δ＜50，当Δ＞40时迭代递推出下一个临近整50ms时间点数据，否则丢弃本周期内采样数据，不做任何处理；

3）时间间隔Δ＝50，正确的时间采样数据；

4）时间间隔Δ＞50，即本中断采样时间滞后或出现中断丢失的情况，需要计算出错过的整50ms的时标，并迭代递推出该时标点的数据，对于Δ%50后的余数，可采用情况2）中的相关处理方法。

结合以上4种现实情况的分析，可以得到具体的时标修正算法流程图，见图2。针对需要修正的时间周期，由上一周期系统时间累加50ms得到当前系统时间，并利用前几个周期的数据点递推得到当前时间点数据，同时依次更新前几个周期内的数据信息。

图2 时标修正算法流程图

2 应用实例

首先，得到未采用时标修正算法的记录文件中时间间隔Δ的相关数据，见图2。其中，时标出现了很多跳点，即非整50ms的时间点。当采用了时标修正算法后，可以得到效果图3。图中时间间隔始终为50ms，完全解决了时标异常的问题。同时，上报的测角经比对，均满足系统精度要求，也验证了数据迭代的正确性。

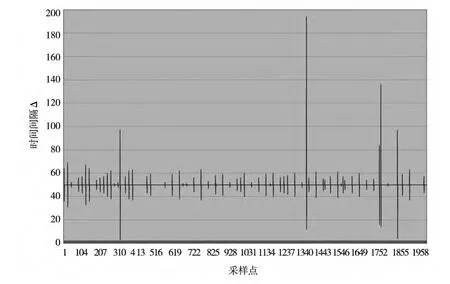
图3 未采用时标修正算法的时标信息图

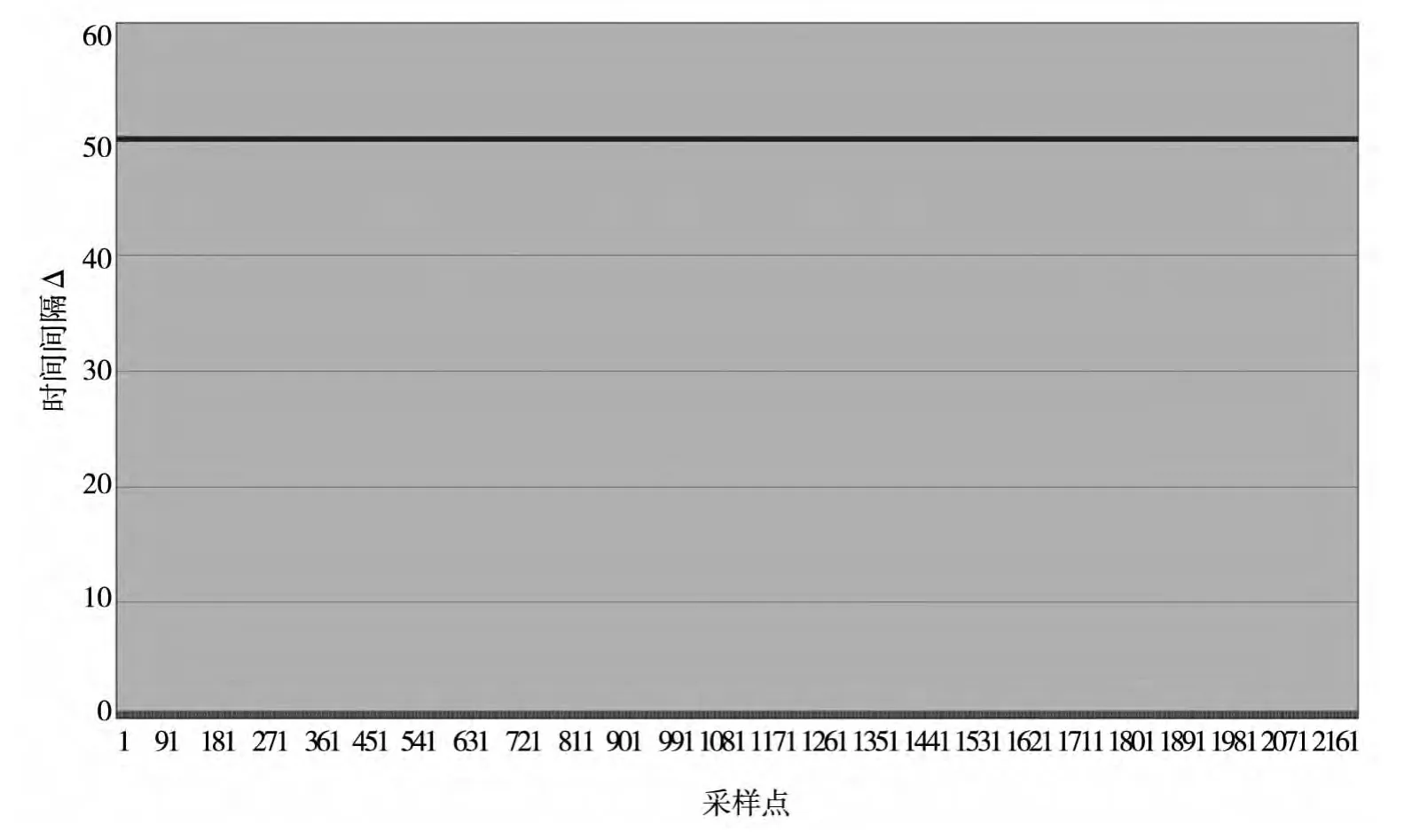
图4 采用时标修正算法的时标信息图

3 结束语

经过验证，该算法能够完全消除上报数据中时标异常的现象，并且已经应用在某9m测控天线中。经过长期运行，时标及测角的精度均满足系统指标要求。该算法简单，容易实施，节约了改造硬件的成本，极大地增强了系统的稳定性和可靠性。

［1］申强.一种在实时控制中数字滤波的算法［J］.通讯与测控，2004，（3）：10－13.

［2］徐孝凯.C＋＋语言基础教程［M］.北京：清华大学出版社，2003.