基于单目视觉图像序列的空间非合作目标相对姿态估计

郝刚涛 杜小平

装备学院，北京 101416

基于单目视觉图像序列的空间非合作目标相对姿态估计

郝刚涛 杜小平

装备学院，北京 101416

非合作目标相对姿态测量是非合作自主交会对接中的难点问题。提出了一种基于单目视觉图像序列的非合作目标相对姿态估计方法。首先建立基于姿态四元数的目标特征点运动观测模型，通过特征点提取、帧间特征点匹配和迭代扩展卡尔曼滤波估计等步骤，成功实现了非合作目标的姿态估计。该方法仅需利用1个单目相机获取图像序列，不需要复杂的视觉传感器和目标上安装人工标记点，也不需要知道目标的几何尺寸等先验信息，且具有较高的估计精度。计算机合成数据仿真和真实图像序列仿真验证了方法的有效性。

单目相机;非合作目标;迭代扩展卡尔曼滤波;姿态估计

空间非合作目标相对姿态测量是非合作自主交会对接导航中的难点问题，已经引起了国内外有关学者和研究机构的广泛关注。目前存在的姿态测量算法大多数是针对合作目标的，这些算法往往依赖于目标上的人工标记点或已知目标的几何结构［1-2］。由于非合作目标没有安装人工标记，且运动情况和空间结构完全或部分未知，因此这些算法不再适用，非合作目标相对姿态测量必须利用视觉系统获取目标自身几何结构或灰度等作为特征信息。

单目相机作为大部分航天器的标准装备，常常是空间探测的有效载荷，开发基于单目视觉的空间非合作目标姿态测量算法能够增加航天器在不需要额外硬件情况下的导航能力;单目相机具有的小巧和低功耗的特点使得它可以集成到微小卫星平台上，这对空间目标探测是重要的，因为使用微小卫星完成在轨服务已经是一个趋势。张世杰等［3］推导了利用单个光学相机实现非合作航天器相对位姿参数测量的迭代算法，该方法需要假设目标航天器详细结构模型已知;张劲锋等［4］将基于单目相机的相对姿态估计问题描述为一个非线性约束优化问题，通过迭代求解特征值问题来确定姿态参数，该方法需要确定较多数量的特征点;岳晓奎等［5］提出基于罗格里斯参数的相对位姿测量方法，该方法需要已知特征点在本体坐标下的坐标。相比于单目视觉，双目视觉能够获取距离信息，但其缺点在于观测范围和测量精度受限于基线长度，且系统安装和标定复杂，徐文福等［6］提出基于双目视觉的空间机器人捕获非合作目标的位姿测量方法，该方法选取太阳帆板支架作为几何特征，初始化阶段需要人的参与，无法做到完全自主;日本宇航开发局利用“在轨可视化环境模拟装置”开展地面试验［7］，采用双目视觉成像获取非合作微小卫星的三维形状，并利用ICP(Iterative Closest Point，ICP)算法估计目标相对姿态，由于算法复杂，无法实现姿态的实时估计。此外，近年来发展的一些非合作目标姿态测量方法往往依赖于能够获取更多目标信息的先进传感器，这些传感器往往更复杂和更昂贵。加拿大Neptec公司开发的TriDAR(Triangulation+LIDAR)视觉系统［8］可以获取目标的3D点云信息，利用ICP算法实现非合作目标的自主导航;美国波尔航空公司研制的三维闪光雷达(3D Flash LIDAR)［9］能够提供目标3D图像，利用提取的三维特征信息实现姿态解算;刘涛等［10］设计的相对导航滤波器能够确定非合作目标相对位姿，该方法需要借助于GPS(Global Position System，GPS)获取追踪航天器到目标航天器的视线仰角和方位角等信息;周军等［11］为实现主星和从星间相对状态的自主精确估计，提出采用陀螺、立体视觉系统和加速度计3者融合的非合作目标相对位姿确定方法。

针对空间非合作目标姿态测量难题，本文建立基于姿态四元数的目标特征点运动观测模型，提出一种基于单目视觉图像序列的非合作目标相对姿态测量方法，该方法无需人工标记和目标的几何信息，仅利用一个单目相机，通过特征点提取和匹配、迭代扩展卡尔曼滤波(Iterated Extended Kalman，Filtering IEKF)估计等步骤实现了非合作目标的姿态解算。

1 坐标系定义及成像观测模型

本文所涉及的坐标系包括相机坐标系OcXcYcZc，目标中心坐标系OoXoYoZo，图像物理坐标系OpXY以及图像像素坐标系OIUV，并假设相机坐标系为惯性坐标系。各坐标系的位置关系如图1所示。目标中心坐标系原点位于非合作目标本体上，但无法确定其具体位置。

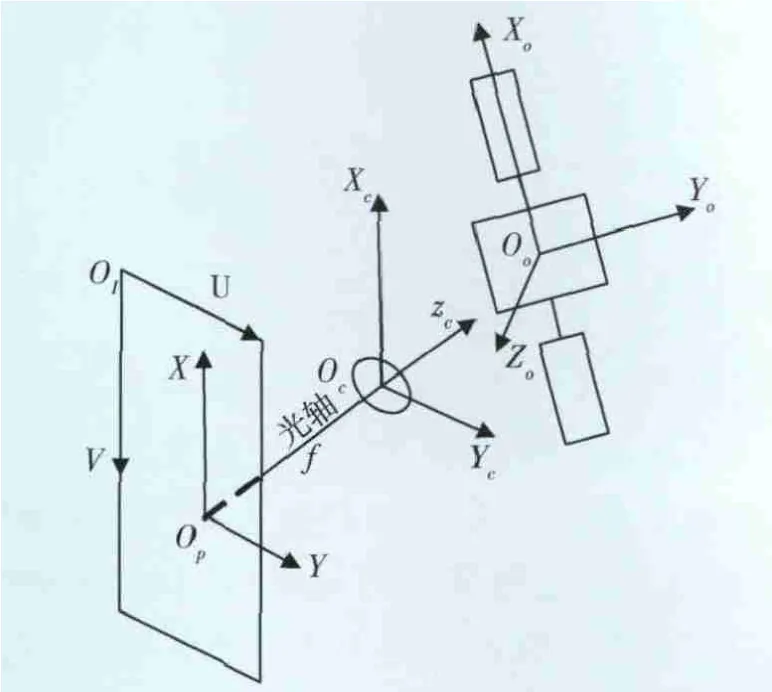
图1 坐标系定义

设成像模型满足映射h:S→P，其中s=(x，y，z)T∈S={(x，y，z)T∈R3，z 〉 0}为空间点在相机坐标系下的坐标，p=(X，Y)T∈P⊂R2为图像物理坐标;设相机焦距为f，则空间点s映射到图像平面上的物理坐标为:

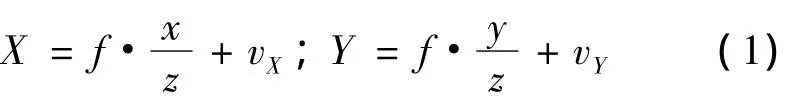
式中，vX和vY为成像噪声，则空间点s的成像观测模型可表示为:

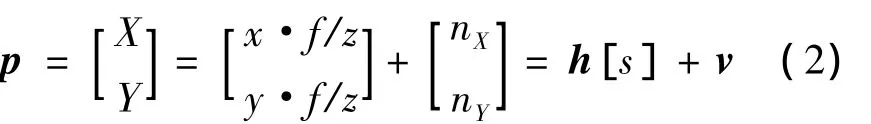
由于实际测量中，图像物理坐标无法直接读取，需要利用图像像素坐标转换得到。设I=(v，u)T∈I⊂R2为图像像素坐标，相机像元尺寸为dx，dy，图像主点坐标为(v0，u0)，则图像物理坐标到图像像素坐标转换关系为

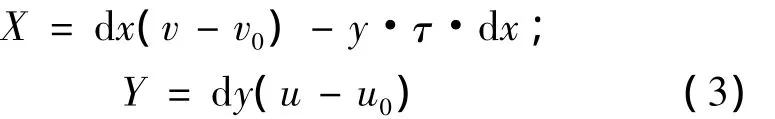
式中τ为倾斜因子，τ，v0，u0通过相机标定得到。

2 基于姿态四元数的目标特征点运动观测模型

由于目标特征点在连续序列图像中的坐标变化能够实时地反映目标相对于相机的运动情况，因此可以将目标的相对运动参数估计问题转化为对其特征点运动参数的估计问题。目标的平动可以看作目标中心坐标系原点在相机坐标系下的位置改变;而目标的姿态运动可以等效于特征点在目标中心坐标系下绕各轴的旋转运动。

在非合作目标上选取M个特征点，设sio=(xi，yi，zi)T为特征点i(i=1，2，…，M)在目标中心坐标下的坐标，sr(t)=(xr(t)，yr(t)，zr(t))T为目标中心坐标系原点在相机坐标系下平动后的坐标，R(t)为t时刻目标中心坐标系到相机坐标系的旋转矩阵，设t时刻特征点i在相机坐标系下的坐标为sic(t)，则有

根据式(2)可得tk时刻特征点i的运动观测模型

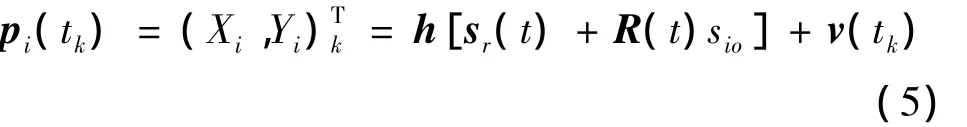
其中，sr(t)可利用Taylor公式表示为

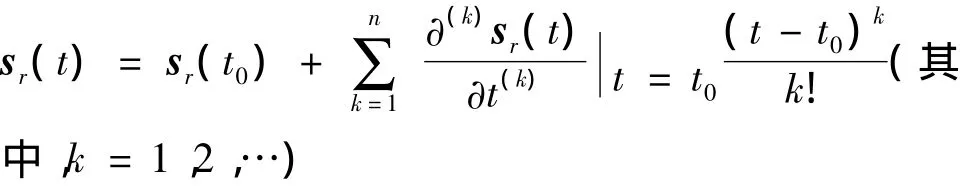
又旋转矩阵R(t)可采用姿态四元数表示为

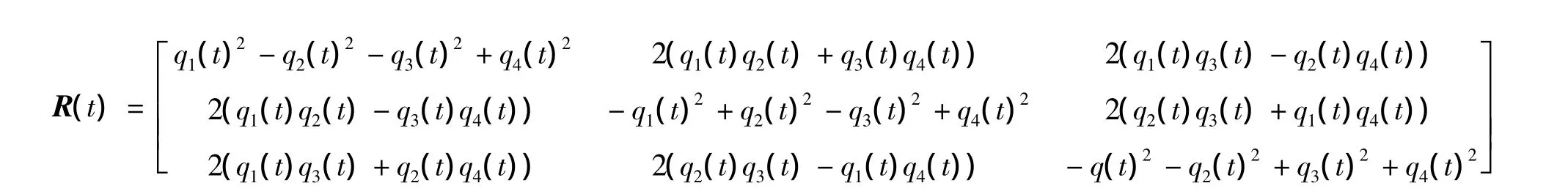
设目标绕XO，YO和ZO轴的旋转速率分别为ωx，ωy和ωz，在非合作目标航天器交会对接导航中，为了实现高精度逼近，目标航天器与跟踪航天器之间的相对运动虽然复杂但较平缓，又考虑到采样间隔很小，假定目标航天器未发生翻滚运动，可以认为在一个采样间隔内目标的转动速度及加速度保持不变，可以用匀速运动模型逼近实际的不规则运动，引入的偏差用系统噪声来补偿。此时可求得:

则特征点运动观测模型的姿态四元数表示形式为

3 非合作目标姿态参数估计

3.1 特征点提取及帧间特征点匹配

由于非合作目标不具有人工标记的特征点，因此，首先需要提取可以反映目标姿态运动的特征点，并实现帧间特征点的自动匹配。假定目标航天器的本体为长方体，但具体尺寸未知。由于太阳帆板需要不断旋转以实现对日定向，故太阳帆板上的点是不稳定的，无法有效反映目标的姿态运动，因此选择较为稳定的本体上的角点作为特征点。

特征点的选择是一项复杂繁琐的工作，由于篇幅所限，本文只介绍其主要步骤，如图2所示。1)对采集到的目标图像经过一系列的图像去噪、滤波和增强等预处理;2)利用Canny算子对其进行边缘提取，生成二值轮廓图像，由于太阳帆板展开后的尺寸往往要比航天器本体大得多，利用这一点，可以识别出目标本体;3)利用Harris算子进行角点检测，并利用Hough变换对目标本体进行直线段检测，对检测出的线段进行长度排序，则最长线段的始点和终点即可确定为长方体本体的顶点，并确定为特征点。由于图像采集时间间隔较小，且相机与目标航天器之间的相对运动平缓，帧间特征点匹配采用运算简单的近邻法实现。

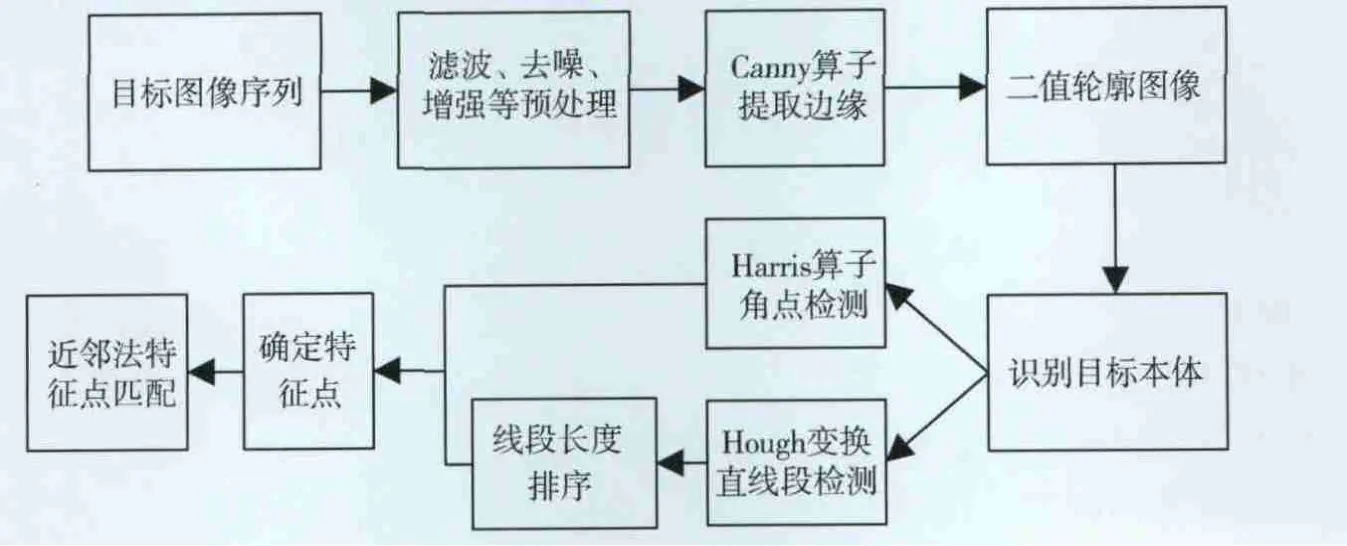
图2 特征点提取及帧间特征点匹配主要步骤

3.2 基于IEKF的姿态估计算法

本文采用IEKF估计算法对目标的姿态参数进行估计，原因在于:1)从式(8)可以看出，特征点运动观测模型是非线性的，IEKF可以更好地处理非线性观测模型下的参数估计问题;2)IEKF算法是一种递归算法，稳定性高，运算速度快，且稍微经过修正即可处理非合作目标运动中部分特征点消失或被遮挡的问题，具有很好的自适应性。

1)状态变量和观测变量的选择。为描述非合作目标的姿态运动，且保证任意时刻的目标运动都以成像平面作为参考，同时考虑到单目相机成像中深度信息zr(t)无法获取，令1/zr(t)作为所有位置变量的归一化系数。设特征点个数为M，此时状态向量为

式中，xi(t)，yi(t)，zi(t)表示t时刻第i个特征点在目标中心坐标系下的坐标。

选择特征点的图像物理坐标Z(t)=［X1(t)，Y1(t)，X2(t)，Y2(t)，…，XM(t)，YM(t)］T作为观测向量，则姿态预估的离散卡尔曼滤波模型为

式中，S(·)为离散系统下状态变量，Φk+1，k为k时刻到k+1时刻的状态转移矩阵，且 Φk+1，k=exp［(tk+1-tk)F］，F为连续时间系统下的状态转移矩阵，Z(k)为观测向量，H(k)为观测矩阵，w(k)和v(k)分别为过程噪声和观测噪声，且相关矩阵cov(w(k))=Rk，cov(v(k))=Qk。假设均为零均值高斯白噪声。下面着重介绍状态转移矩阵Φk+1，k和状态观测矩阵H(k)的确定。

2)状态转移矩阵Φk+1，k的求解。根据式(9)可求得

由连续时间下状态方程˙S(t)=FS(t)+w(t)，

根据 Φk+1，k=exp［(tk+1-tk)F］，Φk+1，k可求解，限于篇幅，不再详细推导。

3)状态观测矩阵H(k)的求解。由式(8)知映射h为非线性的，对h进行线性化处理。根据式(2)，i个特征点的成像观测模型可以写为

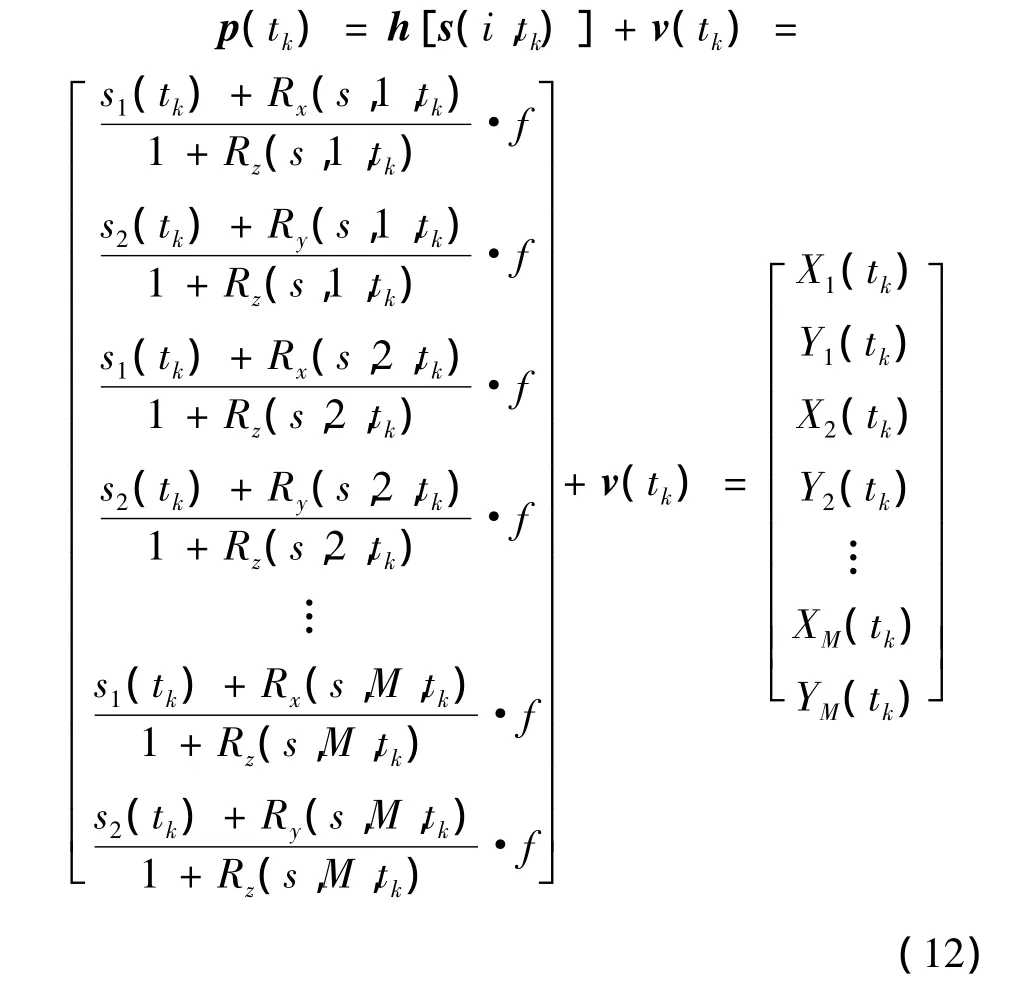
其中，s1(tk)，s2(tk)为归一化后的目标中心坐标系原点坐标，Rx(s，i，tk)，Ry(s，i，tk)，Rz(s，i，tk)分别表示tk时刻第i个特征点的归一化后的目标中心坐标。如

Si为2×3的子矩阵，各元素为

表1 基于IEKF的非合作目标姿态估计公式

综上所述，利用单目视觉图像序列估计姿态参数的原理可用图3表示。首先对单目相机进行标定，建立三维空间到二维图像的非线性映射h;在获取k时刻的目标图像I后，利用特征点提取算法，获取目标图像的特征点集P={p1，p2，…，pn};之后利用特征点匹配算法实现第k帧和k-1帧的特征点匹配，得到k时刻特征点的图像像素坐标(un，vn)k;最后，建立以M个(3≤M≤n)特征点图像物理坐标为观测值、姿态运动参数为状态值的状态方程和观测方程，利用IEKF算法实现姿态参数估计。

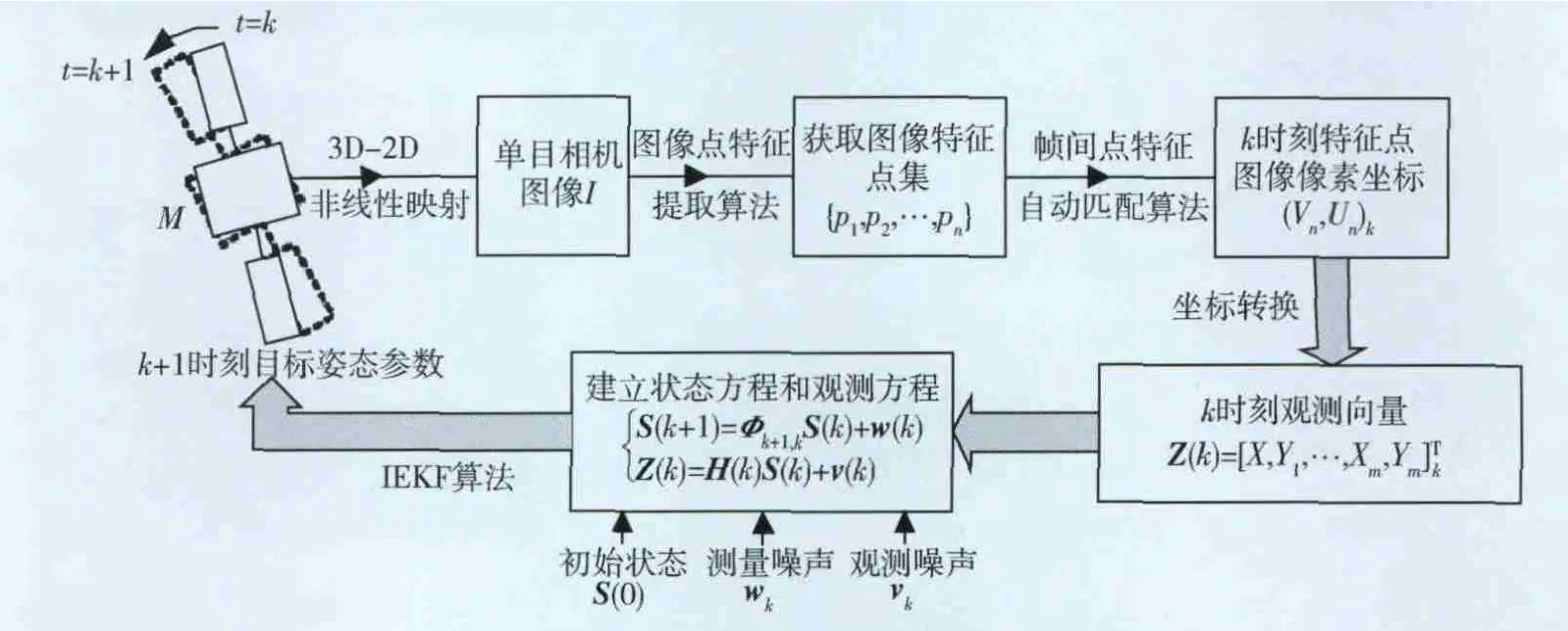
图3 单目视觉姿态估计原理

4 仿真验证

为验证本文所提出的非合作目标姿态估计方法，分别进行了计算机合成图像数据仿真实验和真实图像序列实验。

4.1 计算机合成数据仿真

假设目标为2m×2m×2m的正方体，提取正方体的8个顶点作为特征点。仿真过程中，假设特征点已经提取，且帧间特征点已正确匹配。目标按以下运动参数生成序列图像:旋转速度 ωx=0.02rad/s，ωy=0.025rad/s，ωz=0.015rad/s，平动速度vx=0.025m/s，vy=0.02m/s，vz=0.015m/s，目标的初始位置为(0，0，10)m，采样间隔T=1s，相机的焦距f=20mm，过程噪声和观测噪声均设为零均值高斯白噪声。为了简化计算，假定特征点没有被遮挡，取特征点个数M=4，仿真共进行了300帧的图像序列跟踪，位置和姿态估计结果如图所示。

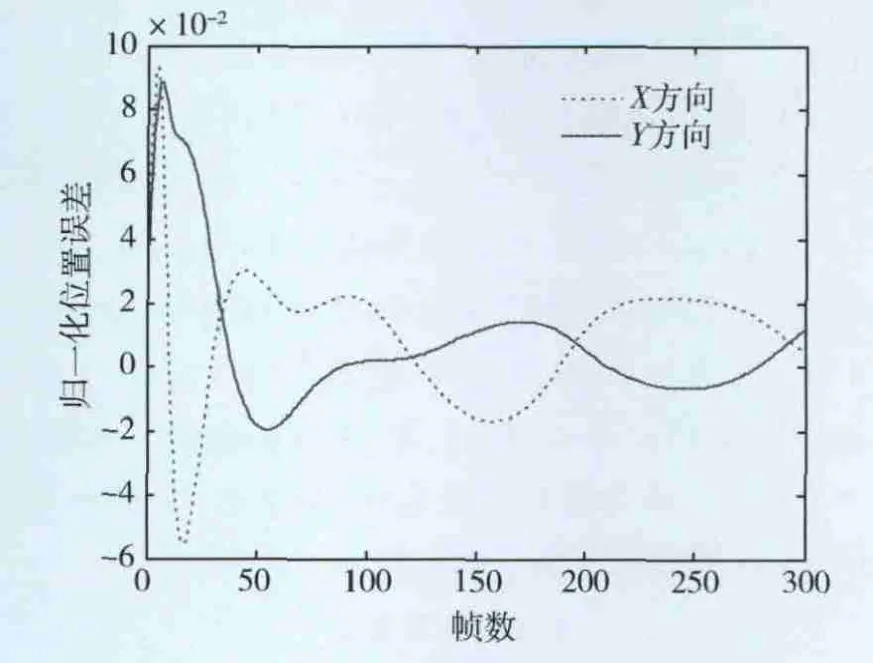
图4 归一化后的位置估计误差变化

从图4中可以看出，大约经过80帧后位置估计开始收敛，但位置误差呈现一定的不稳定性，归一化后的位置误差在-0.02到0.02之间跳动，相对误差较大，虽然整体是收敛的，但收敛时间较长，这可以通过优化IEKF的初值加以改善;

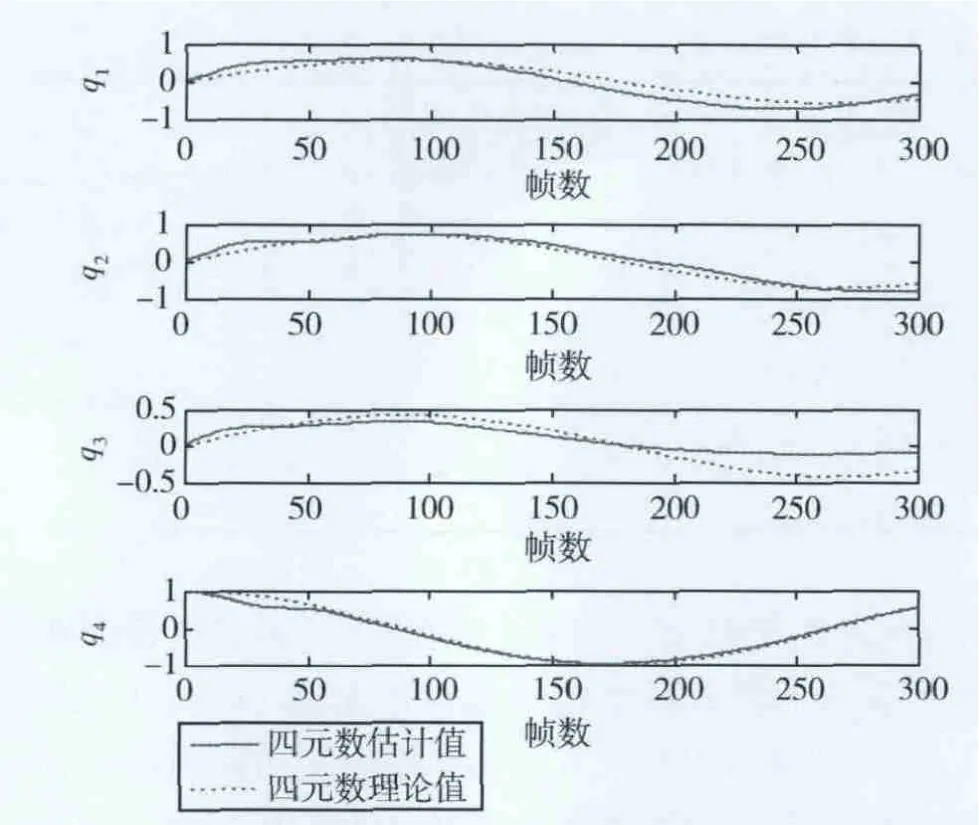
图5 旋转四元数估计值与实际值的比较

图5给出了姿态四元数估计值与理论值的比较，从图中可以看出，q1，q2，q3的估计结果均呈现正弦规律变化，q4的估计值呈现余弦规律变化，这与理论情况完全相符，且估计值与理论值的差异很小，这表明所提出的方法能够成功估计非合作目标的姿态，所建立的基于单目视觉图像序列的IEKF姿态估计模型是正确而有效的。

4.2 真实图像序列仿真

为进一步验证本文提出的姿态估计算法的正确性，利用真实相机采集目标图像序列进行姿态解算。所采用的CCD相机型号为Basler scA780-54fm，像元尺寸dx=dy=8.3μm，分辨率为782×582，最大帧速率为54帧/s，标定后的相机有效焦距f=16.9mm，忽略相机畸变。目标构型如图6所示，利用单轴转台使目标做匀速旋转运动，相关参数如表2所示。特征点提取及帧间特征点匹配采用3.1节所述方法，目标边缘提取及特征点提取结果如图7和8 所示，选择本体上的顶点P1，P2，P3，P4点为特征点。由于硬件条件限制，特征点的提取采用离线方式处理，实验共获取100帧图像序列，采样间隔为1s，仿真结果如图9和10所示。

表2 仿真参数

图6 目标航天器构型

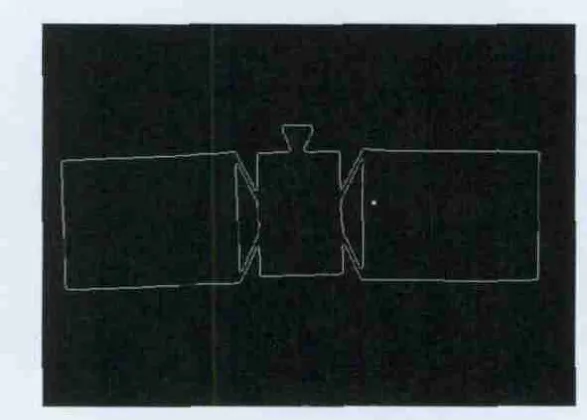
图7 提取到的目标二值轮廓图像

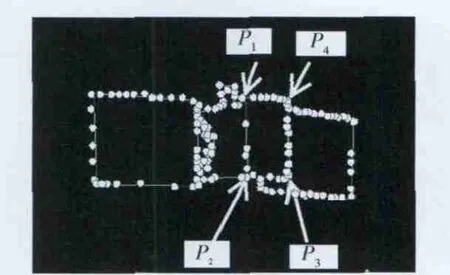
图8 角点提取及特征点选择

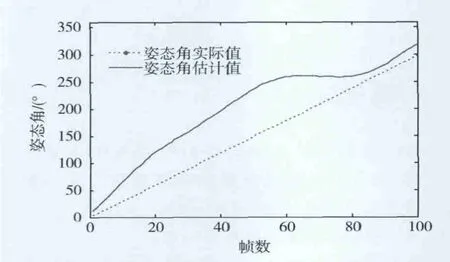
图9 姿态角估计值与实际值的比较

从图9可以看出，在第60帧之前姿态估计与实际值有较大的偏差，大约在第60帧时开始收敛，收敛后的姿态角估计值与实际值的偏差≤10°，相对误差≤3.5%，估计精度较高，但收敛时间较长，因此需要对仿真初值加以优化，以缩短收敛时间。

从特征点的运动轨迹(图10)来看，IEKF估计算法能够很好地实现对特征点的跟踪，从第2节中可知，特征点的运动轨迹能够很好地反映目标的姿态运动，也就表明了基于单目视觉图像序列的非合作目标姿态估计方法的可行性。

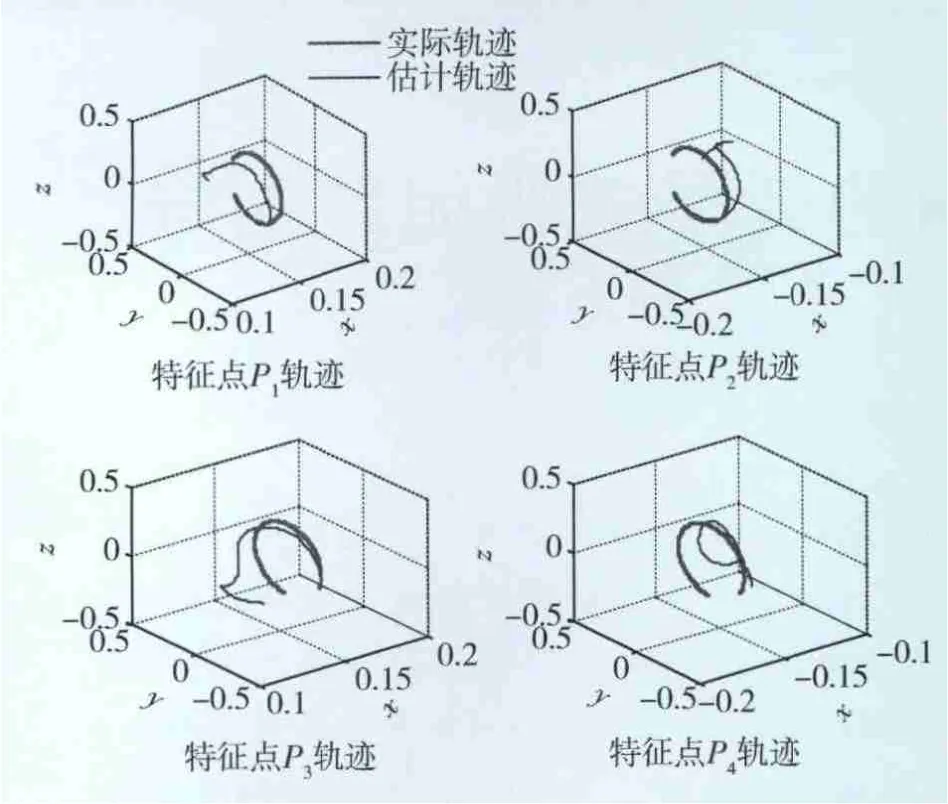
图10 特征点运动轨迹跟踪结果

5 结论

本文提出了一种基于单目视觉图像序列的非合作目标三维姿态估计方法，该方法仅利用1个单目相机，无需目标上安装人工标记，也不需要知道目标的几何尺寸等先验信息，在特征点成功提取和帧间特征点准确匹配的情况下，所采用的IEKF姿态估计算法能够实现较高精度的姿态估计，计算机合成数据仿真和真实图像序列仿真都验证了这一点。但该方法仍然存在一些局限性和需要改进的方面:1)该方法是以帧间特征点精确匹配为前提的，而特征点的提取和匹配非常繁琐，需要花费大量时间，难以实现完全自主和实时处理;2)单目视觉无法获取目标的深度信息，该方法只能估计目标归一化后的位置信息，在实际应用中，如果要实现目标位置和姿态的同时估计，需要借助于激光测距仪等距离传感器;3)不同非合作目标具有不同的自然特征，而该方法是针对一类非合作目标的，如何将该方法扩展到不同的非合作目标姿态估计中是下一步需要努力的。

［1］李建锋，杜小平，张慧星.基于四元数的航天器间相对姿态光学测量方法研究［J］.航天控制，2011，29(2):46-51.(LI Jianfeng，DU Xiaoping，ZHANG Huixing.The Research on Spacecraft Relative State Optical Measurement Based on Quaternion［J］.Aerospace Control，2011，29(2):46-51.)

［2］黄玉明，周世安，王立新，等.航天器位置和姿态的光学测量算法［J］.航天控制，1992，10(3):8-15.(HUANG Yuming，ZHOU Shian，WANG Lixin，et al.Optical Measurement Algorithm of Position＆Attitude for Spacecraft［J］.Aerospace Control，1992，10(3):8-15.)

［3］张世杰，曹喜滨，陈 闽.非合作航天器间相对位姿的单目视觉确定算法［J］.南京理工大学学报，2006，30(5):565-568.(ZHANG Shijie，CAO Xibin，CHEN Min.Monocular Vision based Relative Pose Parameters Determination for Non-cooperative Spacecrafts［J］.Journal of Nanjing University of Science and Technology，2006，30(5):564-568.)

［4］张劲峰，蔡伟，孙承启.基于单目视觉的空间非合作目标相对运动参数估计［J］.空间控制技术与应用，2010，36(2):31-35.(Zhang Jinfeng，Cai Wei，Sun Chengqi.Monocular Vision-Based Relative Motion Parameter Estimation for Non-Cooperative Objects in Space［J］.Aerospace Control and Application，2010，36(2):31-35.)

［5］岳晓奎，侯小娟.基于Rodrigues参数的视觉相对位姿确定算法［J］.宇航学报，2010，31(3):753-757.(Yue Xiaokui，Hou Xiaojuan.Vision-based Relative Position and Attitude Determination Using Rodrigues Parameters［J］.Journal of Astronautics，2010，31(3):753-757.)

［6］Xu W F，Liang B，Li C，et al.Autonomous Rendezvous and Robotic Capturing of Non-cooperative Target in Space［J］.Robotica，2010，28:705-718.

［7］Fuyuto T，Heihachiro K，Shin’ichiro N.Motion Estimation to a Failed Satellite on Orbit Using Stereo Vision and 3D Model Matching［C］.International Conference on Control Automation Robotics＆ Vision(ICARCV)，Singapore，2006:1-8.

［8］Ruel S，Luu T，Berube A.Space Shuttle Testing of the TriDAR 3D Rendezvous and Docking Sensor［J］.Journal of Field Robotics，2012，29(4):535-553.

［9］Miller L K，Masciarelli J，Rohrschneider R，et al.Critical Advancement in Telerobotic Servicing Vision Technology［C］.AIAA Space Conference ＆ Exposition，Anaheim California，2010:1-9.

［10］刘涛，解永春.非合作目标交会相对导航方法研究［J］.航天控制，2006，24(2):48-53.(LIU Tao，XIE Yongchun.A Study on Relative Navigation for Spacecraft Rendezvous with a Non-cooperative Target［J］.Aerospace Control，2006，24(2):48-53.)

［11］周军，白博，于晓洲.一种非合作目标相对位置和姿态确定方法［J］.宇航学报，2011，32(3):516-521.(ZHOU Jun，BAI Bo，YU Xiaozhou.A New Method of Relative Position and Attitude Determination for Non-Cooperative Target［J］.Journal of Astronautics，2011，32(3):516-521.)

Relative Attitude Estimation for Space Non-cooperative Targets Based on Sequence of Monocular Images

HAO Gangtao DU Xiaoping
The Academy of Equipment，Beijing 101416，China

To solve the problem of relative attitude parameters estimation for space non-cooperative targets，a monocular vision-based method is proposed．Based on the attitude quaternion，firstly，the measurement model of feature points is established．Then，the feature points extraction，feature points matching and iterated extendedKalmanfiltering(IEKF)estimation are implemented and relative attitude parameters estimation is finished．This method only needs one monocular camera and can accurately work without the complex vision sensor，manual gauge points and prior information such as geometric information．The experimental results of both synthetic data and the real image sequence show that the algorithm is effective．

Monocular camera;Non-cooperative targets;Iterated extendedKalmanfiltering;Attitude estimation

TP24

A

1006-3242(2014)02-0060-08

2013-04-08

郝刚涛(1986-)，男，河北人，博士研究生，主要研究方向为航天器姿态控制技术和图像配准技术;杜小平(1966-)，女，河北人，博士生导师，主要研究方向为航天装备总体理论与技术、目标探测及信号处理。