基于遗传算法的膜片弹簧的模糊优化设计

唐华林，王剑彬

（南华大学 机械工程学院，湖南 衡阳 421001）

0 引 言

切断和结合发动机的动力传递是离合器的主要用途，同时它能够让汽车可以在起步阶段将发动机与传动系统平顺地接合起来，目的是让汽车能迅速地平稳起步；而在换挡时候它也可以将发动机与传动系统分离，起到减少换挡齿轮之间冲击的作用；运行中突遇较大的动载荷时，传动系统所承受的最大的转矩也能够被有效地限制，可以防止传动系统中各零部件因过载而变形损坏。膜片弹簧作为离合器的关键零件，具有非线性变形特性，膜片弹簧与压盘的接触是依靠整个圆周面进行的，因此压力分布均匀，接触效果好，磨损较均匀，摩擦片磨损后，弹簧压力基本保持不变，同时离合器的踏板力也可以减轻，操纵更为方便。膜片弹簧质量性能的好坏，不仅直接影响离合器的工作性能和工作寿命，而且还能影响离合器与整车的性能匹配。随着国内机械加工制造水平的提高，膜片弹簧的生产加工变得容易。国内外各式汽车均采用膜弹簧离合器，因此离合器的膜片弹簧的结构参数优化设计值得深入研究。

1 膜片弹簧载荷与变形

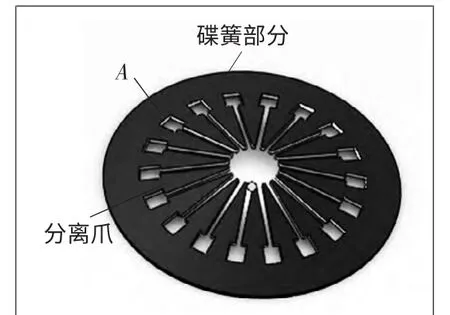
图2 膜片弹簧基本结构图

在膜片弹簧工作时一般会产生各种变形情况，但它碟簧部分内半径处应力是最大的，如图2，A 点应力总是大于其它各点，设σt为切向压缩应力，σr为变曲应力，两者的最大值一般在离合器分离过程中互相垂直的时候［1］，因此A 点处于两向应力状态，按照最大切应力强度理论，在危险点A 的最大当量应力为：

β2为分离爪根部的宽数，β2＝1－δn/［π（r+re）］；

δn为分离爪根部的切槽宽度，mm；N 为膜片弹簧分离爪的数目；re为分离爪前部最宽处半径，mm。

2 离合器膜片弹簧的模糊优化设计

2.1 优化设计数学模型

2.1.1 设计变量

取膜片弹簧的碟簧部分内截锥高H，膜片弹簧与压盘接触半径L，支撑环半径e，碟簧部分内半径r，弹簧片厚度h，大端变形量λ1，则设计变量为

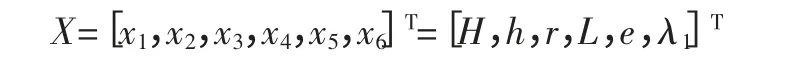
设计变量的变量上、下界模糊约束为:

2.1.2 建立目标函数

第一小子目标：

膜片弹簧是离合器的关键零件，因此膜片弹簧无论从材料、加工工艺、受力分析等方面的研究都是为了膜片弹簧拥有更好的使用性能。然而经过大量的实验观察发现，疲劳断裂是膜片弹簧失效的主要形式，而导致膜片弹簧疲劳断裂的原因是碟簧部分内半径处会产生最大的当量应力，膜片弹簧一般在此处最先产生一些细小的裂纹，然后慢慢地沿着窗孔径发展，最终膜片弹簧疲劳断裂［2］。因此本文以膜片弹簧工作时最大应力点的应力最小为第一个优化目标。

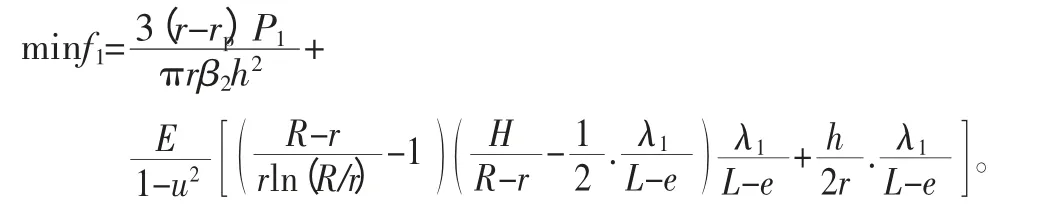
其中R 与离合器结构有关，可先由结构确定。

第二小子目标：

膜片弹簧力学性能的研究是国内学者研究的重点，但是在满足膜片弹簧工作力学性能要求的基础上，同时考虑碟簧体积小、重量轻也成为设计当中的一个方面，以达到进行车辆离合器的设计能够减小离合器的体积和重量，因此，取碟簧体积最小为第二个优化目标，即

设计膜片弹簧离合器时离合器传递的扭矩是一个重要的指标，实际上膜片弹簧工作时，膜片弹簧磨损会产生较大的应力。当然，膜片弹簧的应力跟它的材质、热处理、加工工艺有关。本文以膜片弹簧工作时最大应力点的应力最小同时考虑碟簧的体积小，重量轻。这是个多目标的结构优化问题，考虑使用遗传算法的方便，通过综合分析比较膜片弹簧的各个目标函数，选择2 个权系数ω1和ω2，于是多数目标转化成单目标函数问题：G（x）=ω1f1+ω2f2，其中ω1=0.7，ω2=0.3。

2.1.3 模糊约束条件

1）实验表明，膜片弹簧碟形部分子午截面上表面内缘Ⅰ应力σd1影响点弹力衰减，内缘Ⅱ点应力σt2和Ⅲ点应力σt3影响疲劳断裂［2-3］，故强度约束条件为：

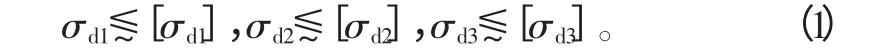
2）为了可以保证设计的膜片弹簧的压紧力Fb与预先设定的压紧力F 相等，则有：

3）膜片弹簧的高厚比应控制在一定的范围内，使它具有离合器使用性能的特性曲线，即

4）磨损后的摩擦片，应使膜片弹簧它的压紧力变化不能太大，这样可以用来保证摩擦片磨损后所使用的离合器仍可以有效地可靠地传递扭矩

5）离合器在彻底分离时膜片弹簧压紧力Fc应该小于工作压紧力，来保证操作方便即

6）膜片弹簧的外、内半径比值和内杠杆比值都应该控制在一定范围内来保证一定的杠杆比要求，即:

7）控制膜片弹簧原始锥底角α 在一定范围内

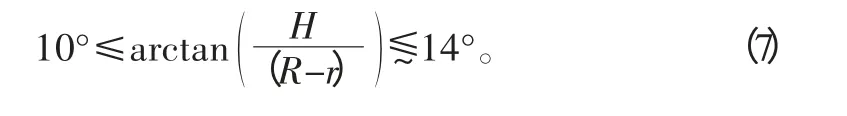
8）根据膜片弹簧结构布置方面的要求，它的大端半径R 与支承环半径L 之差和离合器接合时的加载半径l与内径r 之差都应该一定的范围内，取

2.2 模糊约束的非模糊化处理

模糊集合用不同的λ 值（λ∈［0，1］）去截取模糊集合，水平截集λ 越高，就说明约束的条件越严格，求出的结果可能更安全可靠，如果水平截集λ 较小，则设计计结果经济实用，一般需要同时兼顾这两方面在工程中最优的水平截集，先建立备选集，用不同的水平截集去截取，通过模糊综合评判来确定最终的水平截集λ。λ＊可根据二级模糊评判来确定，λ＊=0.7147，该模糊约束的问题可转变为非模糊约束问题，于是可以表示如下:

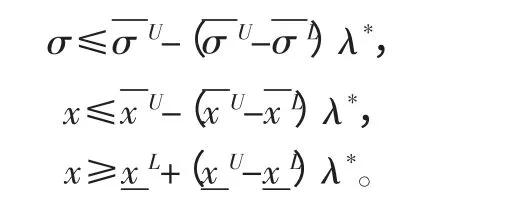
3 设计实例及结果分析

下面以某轿车离合器膜片弹簧为例对其进行结构参数优化设计。已知发动机最大转矩Temax=150 N·m，额定转速ne=3 200 r/min，汽车总质量ma=1 245 kg，膜片弹簧材料选择60Si2MnA，许用当量应力［σ］=1 700 MPa。设定交叉率为Pc=0.689，变异率为Pm=0.006，染色体用浮点数编码方法，遗传代数为120，λ*=0.7147，运用MATLAB GA 工具箱进行模糊优化的结果。得出表1 所示的该轿车离合器膜片弹簧优化设计结果，并与传统设计结果做一比较。

表1 原设计与优化后结果对比

从上述计算的结果可以看出，利用模糊集理论建立其多目标函数模型，运用MATLAB 遗传算法工具箱GA优化设计，其结果均满足约束条件，且目标函数值及膜片弹簧工作时σ当量与弹簧大端加载时所对应的变形量λ1的结果都要优于原设计，达到了应用模糊数学与遗传算法结合进行多目标函数优化的目的。同时膜片弹簧的σ当量减少了6%左右，碟簧部分内半径也减少了2%左右，膜片弹簧的变形量也减少了。

4 数值模拟

本文利用有限元仿真的方法研究膜片弹簧工作时膜片弹簧的当量应力，以及膜片弹簧大端的变形情况。在SolidWorks 中建立仿真模型，然后导入ANSYS Workbench static structural 中分析模块，同时把膜片非线性分析large deflection 打开。当膜片弹簧小端固定，大端加载12 000 N时，从图中可以看出膜片弹簧的大端的最大变形量1.89mm，大端固定，小端加载6 700 N 时膜片弹簧的碟簧内半径处当量应力最大，最大当量应力1351MPa，如图3、图4 所示。

5 结 语

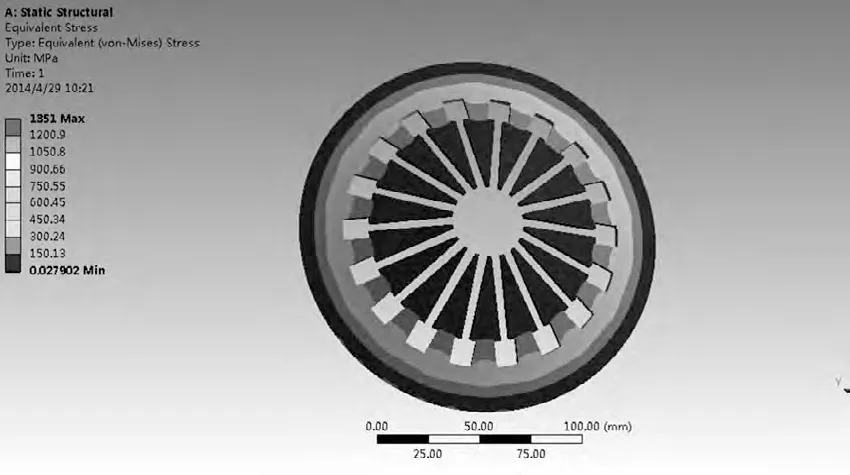
图3 膜片弹簧的当量应力

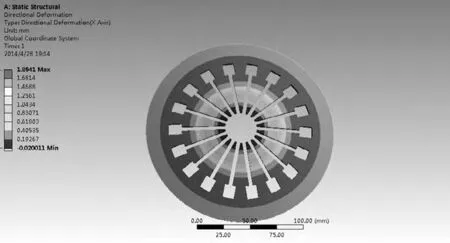
图4 膜片弹簧的大端变形量

本文采用工程上广泛应用的模糊集理论建立多目标的模糊优化数学模型，然后把模糊约束条件转化非模糊条件，运用MATLAB 遗传算法工具箱GA 进行求解，得到整个优化问题的全局最优解，然后运用ANSYS Workbench模拟膜片弹簧当量应力和大端的变形量，从图可知遗传算法工具箱算出的当量应力与有限元软件模拟的值相差2%左右，有限元仿真的变形量比理论计算的变形量稍小，基本上与遗传算法得出的结果一致。因此运用遗传算法与模糊优化设计相结合的方法比普通的模糊优化设计效果明显，具有很好的实际意义。

［1］ 司传胜.汽车膜片弹簧离合器的优化设计［J］.林业机械与木工设备，2004（12）：33-34.

［2］ 范海荣.膜片弹簧疲劳断裂的力学分析［C］//第四届全国弹簧学术会议论文，1991.

［3］ 李戈.汽车离合器膜片弹簧强度的试验研究［D］.镇江：江苏工学院，1991.

［4］ 余超，王剑彬.基于遗传算法的齿轮传动模糊优化设计［J］.机械工程与自动化，2011（1）：54-56.

［5］ 燕展存，王剑彬.基于改进遗传算法的膜片弹簧综合优化设计［J］.常州信息职业技术学院学报，2013（1）：10-14.

［6］ 郭瑞峰，钱志博,关红明.离合器膜片弹簧模糊稳健优化设计［J］.汽车技术，2008（11）：27-30.

［7］ 雷英杰，张善文，李续武.matlab 遗传算法工具箱及应用［M］.西安:西安电子科技大学出版社，2009：23-28.

［8］ 黄洪钟.模糊设计［M］.北京：机械工业出版社，1999.