渔夫捕鱼优化算法的认知无线电频谱分配

项响琴，张沪寅

1.合肥学院网络与智能信息处理重点实验室，合肥 230601

2.武汉大学计算机学院，武汉 430072

渔夫捕鱼优化算法的认知无线电频谱分配

项响琴1，张沪寅2

1.合肥学院网络与智能信息处理重点实验室，合肥 230601

2.武汉大学计算机学院，武汉 430072

针对认知无线电系统中认知用户频谱分配问题，提出一种基于渔夫捕鱼优化算法（SFOA）的频谱分配算法。以系统效益最大化为优化目标，建立认知无线电频谱分配优化的数学模型，采用设置参数少、易于编码实现、寻优能力强的渔夫捕鱼优化算法对模型进行求解，得到空闲频谱最优分配方案，在Matlab 2012平台上进行仿真实验。结果表明，SFOA不仅提高了用户平均系统效益，而且提高了频谱分配效率。

认知无线电；频谱分配；渔夫捕鱼优化算法；移动和收缩搜索

1 引言

随着无线通信技术迅速发展，无线用户的数量急剧增加，频谱资源短缺和频谱利用不均衡现象日益严重。为了解决频谱资源日益紧张和由于固定频谱分配造成的频谱利用率低的问题，Joseph Mitola在软件无线电的基础上提出了认知无线电（Cognitive Radio，CR）的概念。认知无线电可以在不影响用户正常通信的条件下，能够合理利用频谱空穴，提高频谱利用率，因此如何合理、有效利用空闲频谱，具有十分重要的现实意义[1]。

频谱分配必须保证其灵活性，由于频谱信息的不断更新，相应的频谱分配算法也必须满足实时性的要求。针对认知无线电频谱分配问题，已有许多学者进行了相关研究，提出了不同的频谱分配算法，主要包括博弈论、图论着色、议价机制、拍买理论等[2-5]。相对于议价机制、博弈论、拍买理论，基于图论着色理论的频谱分配算法可以提高频谱利用率，计算复杂度较低，但是其存在不公平性、贫困用户等缺点[6]。近年来，有学者把认知无线电频谱分配问题转化成为一个优化问题，然后采用群智能算法进行求解，出现了基于量子遗传算法，离散人工蜂群算法，差分进化算法，二进制粒子群优化算法和混合蛙跳算法等无线电频谱分配算法[7-11]，这些算法通过模拟自然界生物行为，实现信息交流和共享，提高了频谱利用率，实现了认知用户间的公平性。但这些算法都存在各自的不足，如易陷入局部最优等[12]。因此，需要引入新的算法来解决认知无线电频谱分配问题。渔夫捕鱼算法（Optimization Algorithm on Simulating the Fisher Fishing，SFOA）是模拟渔夫捕鱼行为习惯而提出的一种新的智能优化算法[13]，该算法具有原理简单、设置参数少、易于编码实现等优点，在多目标优化领域得到了广泛的应用，并取得比其他群智能算法更好的效果，为解决认知无线电频谱分配问题提供了一种新的研究工具。

为了提高认知无线电频谱利用率，充分利用SFOA全局寻优能力，提出一种基于SFOA的认知无线电频谱分配算法。首先以系统效益最大化为优化目标，建立认知无线电频谱分配优化的数学模型，然后采用SFOA找到空闲频谱最优分配方案，仿真结果表明，SFOA可以有效求解认知无线电的频谱分配问题，使网络系统效益达到最大化。

2 认知无线电频谱分配问题

频谱分配是根据需要接入系统的节点数目及其服务要求，将频谱分配给一个或多个指定节点，图1表示的就是对频谱分配问题的一个简单描述。

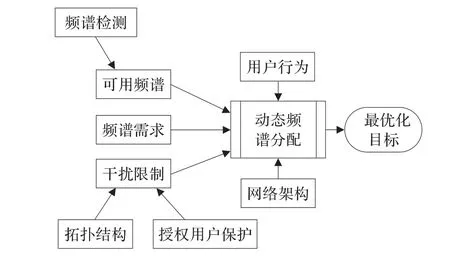
图1 频谱分配问题描述

在效益最大化的频谱分配模型中，由认知用户构成的网络拓扑结构可抽象成图G(V，E，L)，V是顶点集合，一个顶点代表一个认知用户；E是边的集合，若两个认知用户i，j的干扰范围不出现重叠，则ei，j=0，否则ei，j=1；L用来表示次用户的信道可用性。如图2所示[14]。

认知无线网络频谱分配问题可用信道矩阵、效益矩阵、干扰约束矩阵和分配矩阵描述，它们分别定义如下：

（1）信道的可用矩阵L为：

式中，ln，m=1表示认知用户n可以使用信道m；ln，m=0表示认知用户n不能使用信道m。

（2）干扰矩阵C为：

图2 认知无线电系统的模型

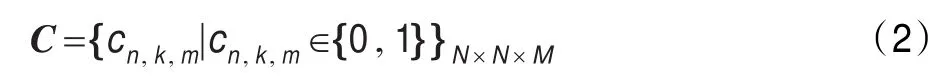
当认知用户n和k同时使用信道m产生干扰，则cn，k，m=1；若认知用户n和k同时使用信道m不产生干扰，则cn，k，m=0。

（3）效益矩阵B为：

其中，B表示认知用户n使用信道m时所获得的效益权重，bn，m=α表示认知用户n使用信道m时获得效用权重为α；bn，m=0表示认知用户n不能够使用信道m。

（4）无干扰的频谱分配矩阵A为：

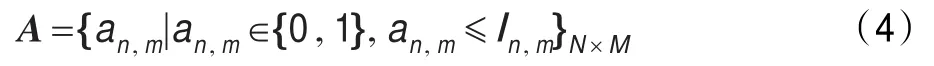
其中，an，m=1表示信道m被分配给了用户n；否则an，m=0。

矩阵A必须满足无干扰限制条件：an，m+ak，m≤1, if cn，k，m=1，∀0＜n，k＜N，0＜m＜M。

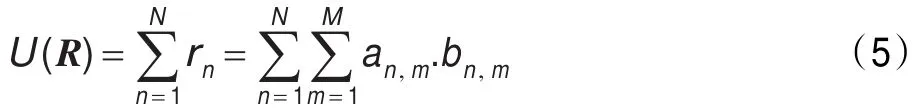
频谱分配技术的主要目的是对可用频谱空间进行合理的分配，使得系统性能得到改善或逼近于最优状态，同时必须考虑计算量及复杂度即效率的问题，因此U越大，分配得到的带宽收益越大，认知无线电频谱分配问题定义为：

3 模拟渔夫捕鱼优化算法

3.1 渔夫捕鱼算法的基本思想

渔夫撒网捕鱼时，开始时很随意地选择江面上一点撒下鱼网，然后在当前下网点的前后左右各撒一次网，而且渔夫总希望每次撒网能捕捉到尽可能多的鱼，而水中鱼的密度越大，能捕捉到的鱼相应就多，因此，渔夫选择在何处撒网的准则为：（1）哪处鱼的密度大，就在哪处下网；（2）何处鱼的密度较大，便移到该处撒网；（3）避免在同一地点重复撒网的现象发生；（4）若发现当前自己所处的位置鱼的密度较大，便收缩撒网范围，以便达到“一网打尽”。渔夫捕鱼算法是一种模拟渔夫捕鱼行为的智能优化算法。

3.2 渔夫捕鱼算法的描述

式中，ε＞0为自定义的较小的常数，那么i渔夫就快速移动，以便跳出局部捕鱼区域（即避免陷入局部最优）。

（4）公告板记录最优渔夫位置，每个渔夫的位置均要与公告板的位置进行比较，若更优，便替换公告板中的位置，算法结束后，公告板值为全局最优值。

（5）若某渔夫在某点处收缩搜索次数达到了最大阈值，但其位置没有改变，那么渔夫重新随机选择一个点进行搜索。

4 SFOA的认知无线电频谱分配

在L，B，C已知的情况下，如何找到最优的无干扰分配矩阵A，使得认知系统效益达到最大化，并尽可能使时间开销最小[15]。从式（6）可知，认知无线电频谱分配问题是一个非线性、多目标优化问题，是一种典型的NP难题，而渔夫捕鱼算法是近年解决复杂NP问题较为理想的方法，因此本文首次将SFOA应用到频谱分配问题中，对公式（6）进行寻优，使U最大，使得认知系统效益达到最大化。

4.1 渔夫位置编码

每一个渔夫位置代表一个潜在的认知无线电频谱分配方案，渔夫位置初始化根据无干扰分配矩阵A进行设计，如果频谱矩阵L中的ln，m=0，那么矩阵A中的an，m=0，为了降低计算时间开销，因此选择L中值为1位置对应A中的元素位置进行编码，对于N=5、M=5的认知无线电频谱分配问题，渔夫位置编码方式如图3所示。

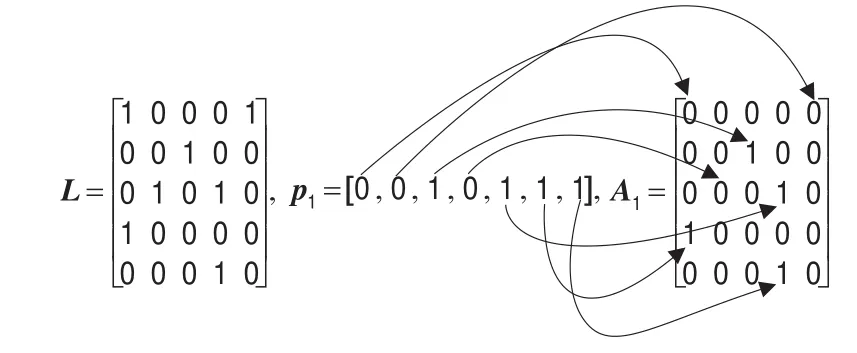
图3 渔夫位置的编码方式

4.2 目标函数设计

认知无线电频谱分配目标是使整个小区内所有认知用户取得的效益总和最大化，因此采用系统效益作为鱼的密度度量函数（目标函数），即

4.3 SFOA的认知无线电频谱分配求解步骤

步骤1给定频谱矩阵L={ln，m|ln，m∈{0，1}N×M，效益矩阵B={bn，m}N×M，干扰矩阵C={cn,k,m|cn,k,m∈{0,1}}N×N×M，L记为1元素对应的n与m，即令L={(n，m)|ln，m=1}。

步骤2随机初始化渔夫的位置，即表示一种可能的频谱分配策略。

步骤3对初始化渔夫的位置，根据式（9）评价渔夫的位置优劣，并找出当前最优捕鱼位置，在公示板公布。

步骤4渔夫在各自的区域进行移动搜索，寻找更优的捕鱼位置。

步骤5如果渔夫找到更优的捕鱼位置，便进入步骤6，否则回到步骤4继续进行移动搜索。

步骤6如果达到收缩操作的阈值CN，便进入到步骤7，不然以最优渔夫位置为中心进行收缩搜索。

步骤7与公示板公示的捕鱼位置进行比较，如果渔夫位置更优，便替代公示板公示的捕鱼位置，并返回到步骤6，不然进入步骤8。

步骤8判断是否满足算法的最大迭代次数，若满足条件，便进入步骤9，不然回到步骤4。

步骤9输出最优捕鱼位置对应的认知无线电频谱分配方案，结束。

基于SFOA的认知无线电频谱分配算法的工作流程如图4。

图4 认知无线电频谱分配算法的工作流程图

5 仿真实验

5.1 仿真环境及对比算法

为了验证SFOA的认知无线电频谱分配算法的效果，在Matlab 2012平台进行仿真测试，并采用文献[13]的粒子群优化算法（PSO）和文献[14]的遗传算法优化（GA）进行对比实验。认知无线电系统的参数见表1。SFOA参数设置为：渔夫个数K=20，移动搜索阈值N=100，收缩搜索阈值CN=20；PSO算法的参数为：粒子数k=20，c1=c2=2，惯性权重w=0.5；GA的参数为：个体数为k= 20，pc=0.9，pm=0.1，所有算法的最大迭代次数均为500。

表1 仿真参数

5.2 结果与分析

5.2.1 收敛速度对比

当M=10，N=10时，GA、PSO和SFOA的系统效益变化曲线如图5所示，从图5可知，随着迭代次数的增加，认知无线电系统效益不断增加，SFOA在200代左右，系统效益就达到最优，即找到了认知无线电频谱分配的全局最优解，而GA、PSO分别在280、300代左右才找到最优解，而且系统效益明显低于SFOA，这表明SFOA的收敛速度要快于GA、PSO，而且找到了比GA、PSO更优的无线电系统频谱分配方案。

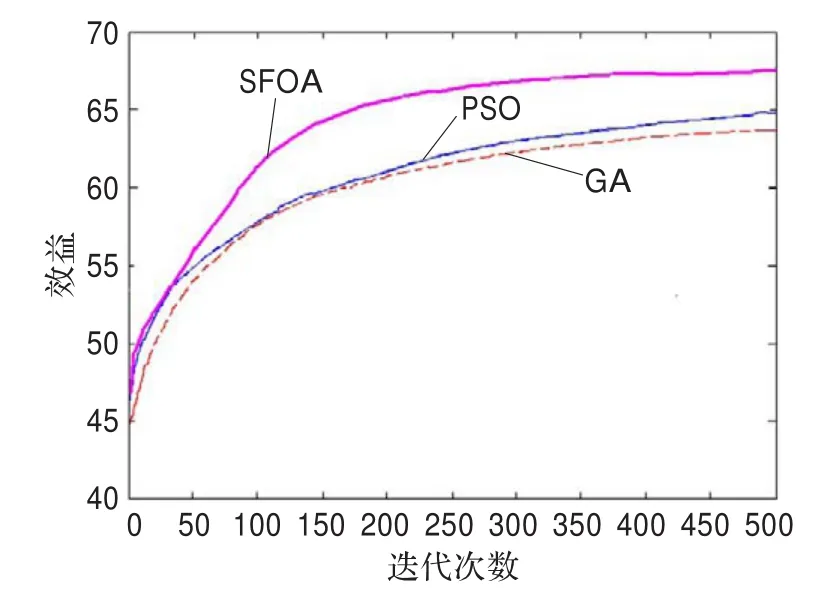
图5 不同算法的收敛速度比较

5.2.2 系统效益与可用频谱数之间的变化关系

在N=10条件下，随着可用频谱数的增加，系统效益的变化趋势如图6所示。从图6可知，随着可用频谱数增加，用户可以选择频谱增多，用户间干扰减小，系统效益逐渐增加，而且SFOA的频谱分配算法的系统效益明显优于GA、PSO的系统效益，对比结果表明，相对于GA、PSO，SFOA可以使系统效益更加最大化。

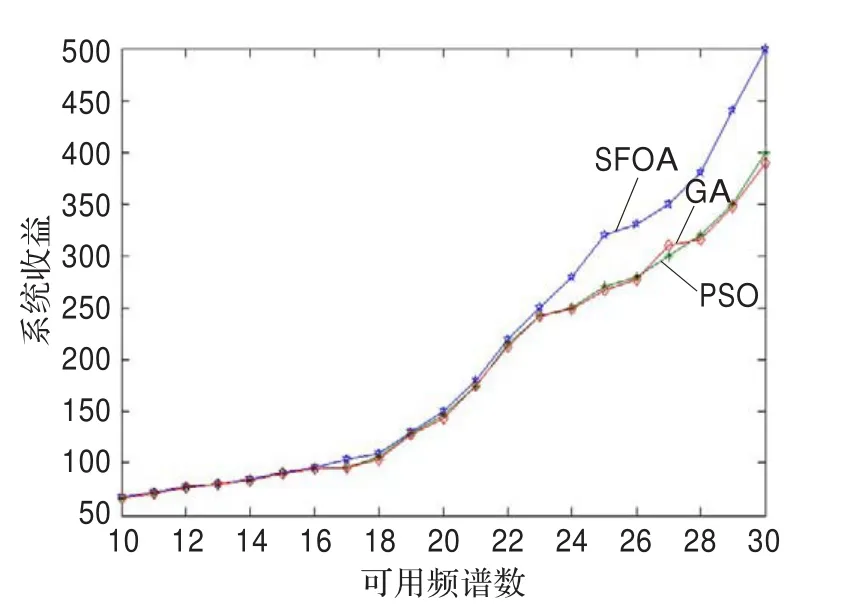
图6 系统效益与频谱数的变化关系

5.2.3 系统效益与用户数之间的变化关系

当M=20时，随着用户数N变化，系统效益变化趋势如图7所示。从图7可知，随着N增加，用户之间的频谱竞争越来越激烈，用户之间干扰频率增加，系统效益慢慢递减，但是SFOA的频谱分配算法的系统效益减幅明显要小于GA、PSO的系统效益。

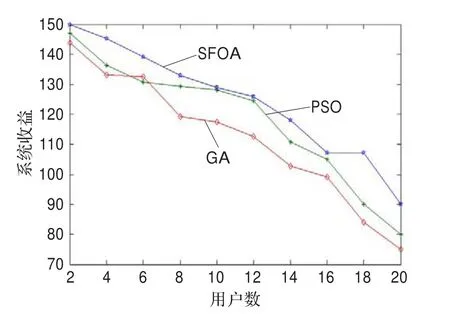
图7 N变化时系统效益

5.2.4 网络效益与实验次数之间的变化关系

以最大网络总效益为目标函数、当N=10，M=20时，在不同初始条件下的实验结果如图8所示。不同实验中B，L，C不同，同一次实验中GA、PSO、SFOA的频谱分配算法采用的B，L，C相同。从图8可知，在大多数情况下，SFOA的无线电频谱分配算法获得的网络效益要明显优于GA、PSO获得的网络效益，只有少数点的网络效益相差不大，这说明基于SFOA的无线电频谱分配算法提高了认知系统的效益，可以较好地满足认知无线电网络频谱分配要求。

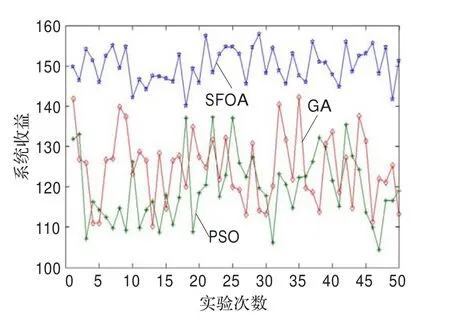
图8 不同算法的网络效益对比

6 结语

针对认知无线电系统的频谱分配问题，提出了一种基于SFOA的认知无线电频谱分配算法，并通过具体仿真实验测试性能。仿真结果表明，相对于PSO、GA，SFOA可以找到更优的认知无线电系统频谱分配方案，实现网络效益的最大化，可以满足更广泛的认知无线电网络应用需求。

[1]滑楠，曹志刚.认知无线电网络路由研究综述[J].电子学报，2010，38（4）：910-918.

[2]Rahimi-Vahed A，Mirzaei A H.Solving a bi-criteria permutation flow-shop problem using shuffled frog-leaping algorithm[J].Soft Computing，2008，12（5）：435-452.

[3]宁国勤，张静.基于时间预测的多跳频谱切换算法研究[J].计算机工程与应用，2013，49（13）：71-75.

[4]王钦辉，叶保留，田宇，等.认知无线电网络中频谱分配算法[J].电子学报，2012，40（1）：147-154.

[5]Jie Jia，Wang Chuang，Zhang Zhaoyang，et al.Dynamic spectrum assignment based on graph coloring in cognitive radio network[J].Journal of Northeastern University：Natural Science，2012（3）：336-339.

[6]彭振，赵知劲，郑仕链.基于混合蛙跳算法的认知无线电频谱分配[J].计算机工程，2010，36（6）：210-217.

[7]柴争义，刘芳.基于免疫克隆选择优化的认知无线网络频谱分配[J].通信学报，2010，31（11）：92-100.

[8]知劲，彭振，郑仕链，等.基于量子遗传算法的认知无线电频谱分配[J].物理学报，2009，58（2）：1358-1363.

[9]Chuang Liyeh，Tsai Shengwei，Yang Chenghong.Chaotic catfish particle swarm optimization for solving global numerical optimization problems[J].Applied Mathematics and Computation，2011，217.

[10]Zhao Zhijing，Peng Zheng，Zheng Shilian，et al.Cognitive radio spectrum allocation using evolution algorithms[J]. IEEE Trans on Wireless Communications，2009，8（9）：4421-4425.

[11]唐万斌，喻火根，李少谦.基于信道预测的认知无线电混合频谱切换算法[J].计算机工程与应用，2012，48（27）：17-21.

[12]张北伟，朱云龙，胡琨元.基于粒子群算法的认知无线电频谱分配算法[J].计算机应用，2011，32（12）：3184-3214.

[13]王勇，陈建荣，庞兴.一种模拟渔夫捕鱼的寻优算法[J].计算机应用研究，2008，26（8）：2888-2890.

[14]朱冰莲，裴光术，张磊，等.认知无线电网络中系统效益最大化的频谱分配[J].计算机工程，2012，38（3）：107-109.

[15]肖淑艳，孙茜，衡芹，等.基于D-S理论的认知无线电频谱感知算法[J].计算机工程与应用，2011，47（33）：91-93.

XIANG Xiangqin1,ZHANG Huyin2

1.Key Lab of Network and Intelligent Information Processing,Hefei University,Hefei 230601,China
2.College of Computer,Wuhan University,Wuhan 430072,China

This paper proposes a novel spectrum allocation method of cognitive radio based on Optimization Algorithm on Simulating the Fisher Fishing（SFOA）to solve the spectrum allocation problem of cognitive radio system.Spectrum allocation optimization mathematical model of the cognitive radio is established whose maximum benefit is taken as the optimization goal,and then the optimal spectrum allocation scheme is obtained by SFOA which has less parameters, encodes easily,strong ability.The simulation experiment is carried out to test the performance of SFOA algorithm.The results show that the proposed method not only increases users mean system utility,but also improves the efficiency of spectrum allocation.

cognitive radio;spectrum allocation;Optimization Algorithm on Simulating the Fisher Fishing（SFOA）;moving and diminishing search

A

TN914

10.3778/j.issn.1002-8331.1308-0152

XIANG Xiangqin,ZHANG Huyin.Spectrum allocation of cognitive radio system based on SFOA.Computer Engineering and Applications,2014,50（6）：72-76.

国家自然科学基金（No.61272454）。

项响琴（1976—），女，讲师，主要研究领域为数据挖掘与智能软件；张沪寅（1962—），男，博士，教授，主要研究领域为网络体系结构，高性能计算，e-Learning。

2013-08-14

2013-10-18

1002-8331（2014）06-0072-05

CNKI网络优先出版：2014-01-15，http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1308-0152.html