子模型法在拱坝泄水底孔应力分析中的应用

郭晓晶，徐谨谨

（浙江省钱塘江管理局勘测设计院，浙江杭州310016）

子模型法在拱坝泄水底孔应力分析中的应用

郭晓晶，徐谨谨

（浙江省钱塘江管理局勘测设计院，浙江杭州310016）

应用有限元子模型法对某工程高水头薄拱坝泄水底孔进行了三维有限元计算，分析了底孔有压段的孔口应力及上、下游悬臂结构的应力状态。结果表明上游悬臂和坝体交接处底孔侧壁部位顺水流向拉应力较大，而传统的平面有限元法计算拱坝泄水孔口的应力时，认为顺水流向的应力比较小；又通过多方案的计算，对不同模型计算结果的差异进行了分析。相对于传统计算方法，用子模型法对高水头薄拱坝泄水孔口进行有限元分析，可以大大降低计算工作量，减少计算所花费的时间，并有利于提高计算的精度。

底孔；上下游悬臂；子模型法；三维有限元

目前采用三维有限元进行坝体孔口应力分析研究，常用的有以下三种方法［1－2］：① 把整个模型有限元网格细化进行计算，这是一种费时费力的方法；②对所关心区域（孔口）进行加密处理，其他部位大网格划分，中间采用过渡单元，这一方法为了得到较准确的结果，必须将所关心部位的网格划分的很密，但是如果相邻单元的尺寸相差过于悬殊，可能会引起较大的计算误差；③首先对整体模型网格局部加密，就是把关心区域（孔口）附近的网格划分的比其他区域稍微密一些，以便较准确的反映关心区域（孔口）的应力分布情况，而其他区域的网格密度可以稀疏一些，中间采用过渡单元，这样可以得到较准确的边界条件；在此基础上将关心区域（孔口）取出进行精细加密，再将由整体模型计算得到的边界条件施加上去，这样不仅使所关心区域（孔口）的结果更加准确，而且可以大大降低计算工作量，减少计算所花费的时间，节省计算机内存，这种方法叫做子模型法，整体模型称为主模型，局部模型称为子模型。

1 有限元子模型法计算的基本步骤

子模型法的基本步骤［2－14］是：

（1）生成并分析粗糙模型

生成整体结构的模型并分析。整体模型（即粗糙模型）的网格划分相对于子模型的网格是较粗糙的。分析类型可以是静态或瞬态的，其操作步骤与其它一般的分析步骤相同。

（2）生成子模型

在初始状态清空数据库（或者退出并重启动程序），创建不同的文件以防止粗糙模型文件被覆盖；进入前处理建立子模型，建立的子模型应使用与粗糙模型相同的单元类型，指定相同的单元实参和材料特征。此外，子模型的位置（相对于全局坐标）应与粗糙模型的相应部分相同；指定合适的节点旋转位移。

（3）生成切割边界插值

用户定义切割边界的节点，程序引用粗糙模型结果，利用插值方法计算这些节点上的自由度数值（位移等）。对于子模型切割边界上的所有节点，程序利用粗糙模型网格中相应的单元确定自由度数值，然后利用这些数值用单元形状功能插值方法插值到切割边界上。

（4）子模型求解

指定分析类型和设置分析选项，加入插值的自由度数值，施加其它的荷载和边界条件，指定荷载步选项，再对子模型求解。

（5）验证切割边界和应力集中位置的距离是否足够

可以通过比较切割边界上的应力结果与粗糙模型相应位置的结果是否一致来验证。如果符合得很好，证明切割边界的选取是合理的。如果不符合就要重新定义离关心的部分稍远一些的切割边界重新生成和计算子模型。

2 实例分析

2.1 工程概况

某枢纽工程主要建筑物包括拦河坝、右岸地下厂房、引水及泄水建筑物等。拦河坝为对数螺旋线双曲薄拱坝，最大坝高250 m。坝身泄洪建筑物由三个表孔、二个深孔、一个底孔和一个临时底孔组成，分三层分别布置于坝身不同坝段，该水电站坝身坝体较薄，且坝体与闸墩不分缝，坝体应力大，设计水头高，弧门承受水推力大、上下游伸出坝体的悬臂长；受坝体应力影响，孔口应力较大，受布置影响，上、下游悬臂较长，使得拱坝孔口情况比较复杂。本文以拱坝底孔为研究对象，进行三维有限元计算分析，为底孔设计提供参考。

2.2 计算基本参数

坝顶高程：2 460m

建基面高程：2 210m

水重度：10 kN／m3

混凝土重度：24 kN／m3

钢筋混凝土重度：25 kN／m3

混凝土静弹模量：20 000 MPa

混凝土泊淞比：0.167

混凝土热胀系数：0.00001／℃

混凝土线膨胀系数：αc＝0.1×10－41／℃

上游正常蓄水位：2 452.0m

相应下游水位：2 239.5m

混凝土强度等级及弹性模量见表1。

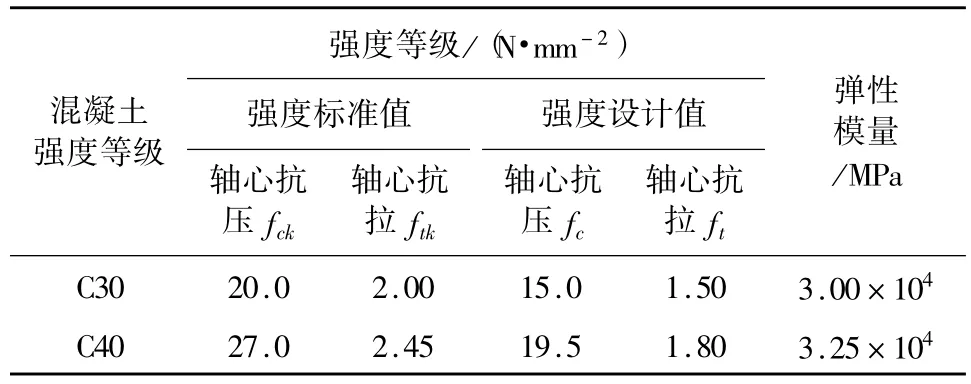
表1 混凝土强度及弹性模量

2.3 计算工况

工况1：自重＋上游正常蓄水位（2 452.0 m）＋相应下游水位（2 239.5m）＋弧门推力

2.4 计算模型的建立及网格划分

（1）坐标系

拱坝整体模型计算坐标系规定：水流方向为 X轴方向，向上游为正；沿高度方向为 Y轴方向，向上为正；坝轴线方向为 Z轴方向，向左岸为正。子模型计算坐标系正向规定与整体模型一致。

（2）整体模型建立及网格划分

拱坝整体模型包括地基、整个坝体，地基上、下游边界及底部厚度均取≥1倍坝高，整体模型网格剖分采用8节点六面体单元，部分通过四面体实体单元进行过渡。泄水孔口周围、上下游悬臂单元网格划分不大于100 cm×100 cm×100 cm，其他部位的单元尺寸逐渐放大，中间用过渡单元过渡。拱坝整体有限元模型见图1，整体模型坝体部分有限元模型见图2，单元总数128 004个，节点总数114 585个。

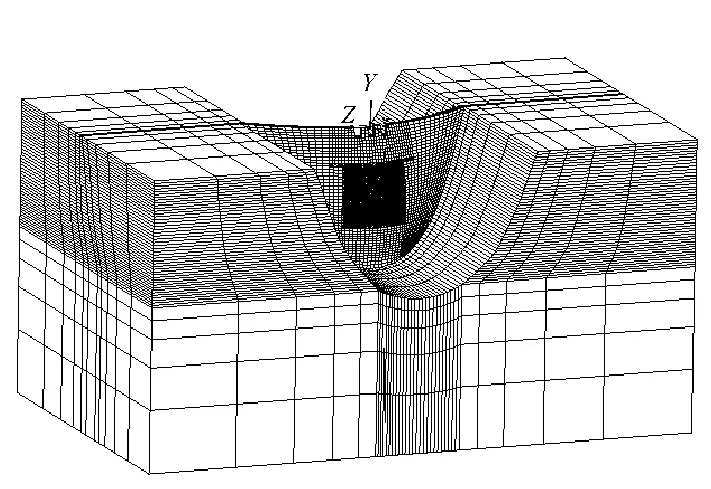
图1 拱坝整体有限元模型

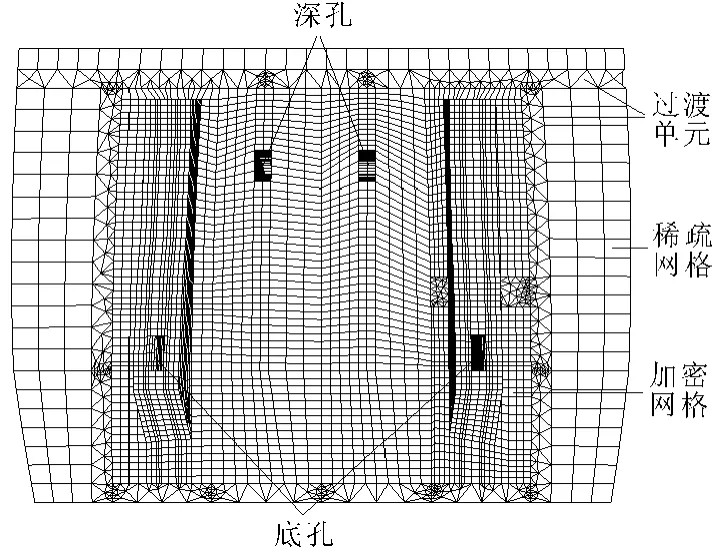
图2 坝体孔口局部加密有限元模型

（3）子模型建立及网格划分

底孔子模型选取其位置所在的单个坝段，顶部至2 392.0m高程，底部至2 290.0 m高程作为计算子模型（28m×102 m）的边界条件。计算单元划分基本采用八节点六面体实体单元，部分通过四面体实体单元过渡，孔口周围单元网格划分不大于30 cm ×30 cm×30 cm，其他部位的单元尺寸逐渐放大。子模型计算的边界条件是整体模型求解的位移插值。底孔有悬臂有限元子模型见图3，单元总数177 815个，节点总数189 511个。

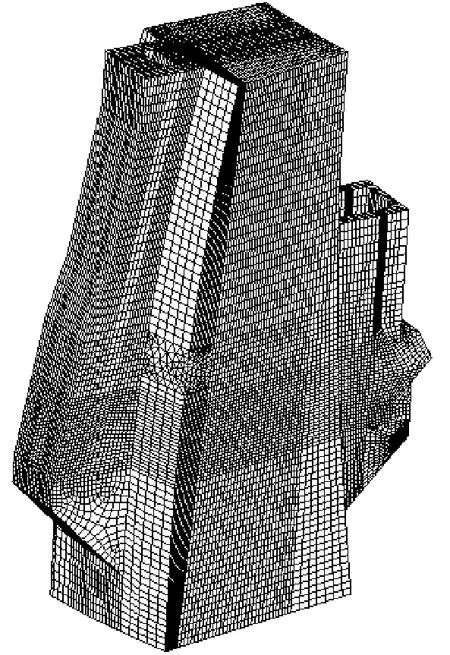
图3 底孔子模型有限元模型

3 计算结果分析

3.1 主要部位计算结果

（1）底孔流道侧壁Y向和第一主应力基本都处于拉应力状态，流道出口侧壁拉应力最大，Y向应力达到2.2 MPa，第一主应力达到2.6 MPa；

（2）竖井附近底孔侧壁 X和Y向拉应力均较大，X向应力最大达到1.0 MPa，且沿坝轴线方向分布深度较大；Y向应力最大达到1.4 MPa，但沿坝轴线方向衰减较快；

（3）下游悬臂与坝体交接闸墩内侧面X向和第一主应力也较大，且沿坝轴线分布深度较大，X向应力为1.2 MPa，第一主应力为1.7 MPa；Z向应力较小，基本为压应力；

（4）上游悬臂与坝体交界处底孔侧壁表面X向拉应力较大，为1.5 MPa，沿坝轴线方向分布深度较大。

3.2 计算结果分析

由计算结果可以看出：

（1）由于拱坝拱推力的作用，孔口周边侧向坝体应力较大，使得底孔流道侧壁 Y向应力较大，与传统的平面有限元法观点一致；

（2）坝体内设置预留竖井，必然会削弱坝体结构，产生应力集中现象，但是这种影响仅是局部的，主要集中在竖井周边；

（3）在悬臂自重的作用下，使得下游悬臂与坝体交接闸墩内侧面出现较大拉应力；

（4）上游悬臂与坝体交界处底孔侧壁面 X（顺水流）向出现较大拉应力，与传统的复变函数、平面有限元法［15］相矛盾，这两种方法认为沿水流方向的拉应力比较小，具体原因见下文分析。

3.3 孔口应力影响因素分析

（1）多方案比较

拱坝坝身结构较薄、增设孔口上、下游大悬臂使孔口受力情况更加复杂化，为了研究产生上游悬臂与坝体交界处底孔侧壁面X（顺水流）向拉应力的原因，本文对不同荷载和不同孔口体型进行了多方案的计算分析。方案表见表2。

（2）计算结果

各方案上游悬臂与坝体交接处底孔侧壁面应力对比见表3。

表2 方案表

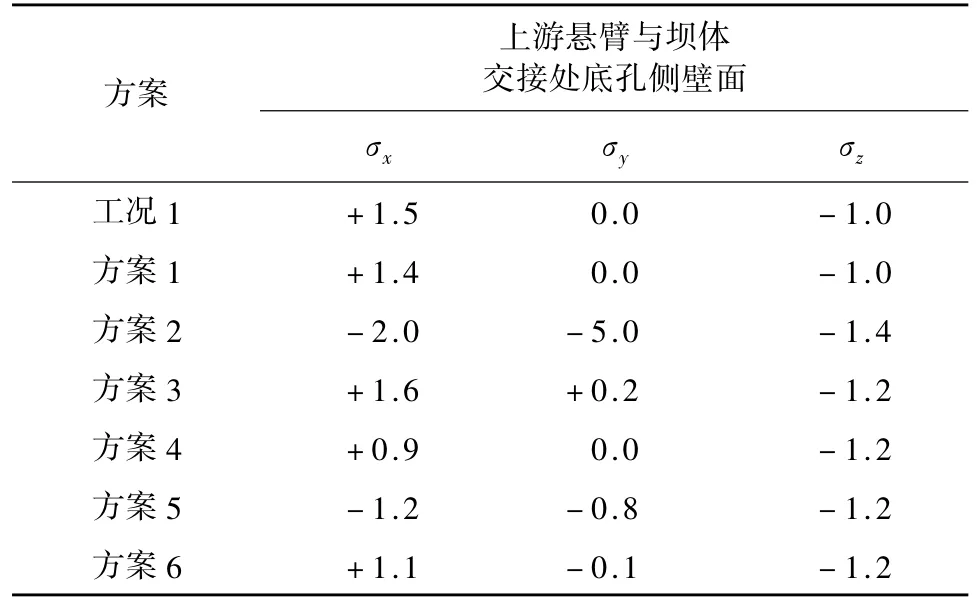
表3 各方案特征部位拉应力对比 单位：MPa

由计算结果表3可以看出：

方案1：竖向坝体应力对上游悬臂与坝体交接处底孔侧壁面影响较小，相比工况1，顺水流方向（X向）拉应力降低了7%；

方案2：侧向坝体应力对上游悬臂与坝体交接处底孔侧壁面影响非常大，相比工况1，顺水流方向（X向）拉应力由受拉变成全部受压；

方案3：温降荷载对上游悬臂与坝体交接处底孔侧壁面影响较小，相比工况1，顺水流方向（X向）拉应力增大了7%；

方案4：温升荷载对上游悬臂与坝体交接处底孔侧壁面影响较大，相比工况1，顺水流方向（X向）拉应力降低了40%；

方案5：上、下游悬臂对上游悬臂与坝体交接处底孔侧壁面影响非常大，相比工况1，顺水流方向（X向）拉应力由受拉变成全部受压；

方案6：上游悬臂底孔附近加厚4 m对上游悬臂与坝体交接处底孔侧壁面影响较大，相比工况1，顺水流方向（X向）拉应力降低了27%。

（3）计算结果对比分析

从以上计算结果可知，不同荷载方案中方案1（边界条件没有施加竖向坝体应力）和方案3（增加温降荷载）对上游悬臂与坝体交接处底孔侧壁面影响较小，而方案2（边界条件没有施加侧向坝体应力）和方案4（增加温升荷载）影响较大，但是方案2在实际情况中是不可能发生的，而方案4随着拱坝温度应力的增加，可以抵消一部分坝体侧向应力，从而使底孔侧壁顺水流方向（X向）拉应力变小。对于不同体型方案，上游悬臂是使上游悬臂与坝体交接处底孔侧壁面顺水流方向（X向）由压应力变为拉应力的主要原因，坝体设悬臂结构后，其重力通过泄水孔周边混凝土传递到坝体，改变了孔口周边的应力分布；方案6（上游悬臂底孔附近加厚4m）上游悬臂与坝体接触面加大，减弱了上游悬臂对孔口的影响。从以上分析可知，子模型法在高水头薄拱坝泄水孔有限元计算分析中能够反映孔口结构的实际受力情况。

4 结 论

（1）子模型法不仅是解决泄水孔口应力分析的有效途径，而且可以大大降低计算工作量，减少计算所花费的时间，并且其边界条件更为精密，分析精度更高；

（2）上游悬臂与坝体交界处底孔侧壁顺水流向（X向）应力较大，与传统的复变函数、平面有限元法相矛盾，通过多方案计算分析可知，由于悬臂的存在，使得上游悬臂与坝体交界处底孔侧壁顺水流向应力由压应力变拉应力，应注意此处的连接，确保悬臂结构的稳定。

（3）将上游悬臂加厚，可以改善上游悬臂和坝体交接处底孔侧壁X（顺水流）向应力。

［1］ 朱伯芳，高季章，陈祖煜，等.拱坝设计与研究［M］.北京：中国水利水电出版社，2002：758-762.

［3］ Desai C S，Abel J F.Introduction to the finite element method［M］.New York：Van Nostrand Reiinhold Co，1972.

［4］ Papanikos P，Meguid SA，Stjepanovic Z.Three-dimensional nonlinear finite element analysis of dovetail joints in aero-engine discs［J］.Finite Elements in Analysis and Design，1998，29：173-186

［5］ 王艳辉，伍建国，朱壮瑞，等.子模型法在车身静态分析中的应用［J］.沙洲职业工学院学报，2002，5（1）：11-14.

［6］ 马震岳，孙万泉.高拱坝坝后背管结构静动力分析［J］.水力发电，2003，29（7）：32-35.

［7］ 徐 伟，李 智，张肖宁.子模型法在大跨径斜拉桥桥面结构分析中的应用［J］.土木工程学报，2004，37（6）：30-34.

［8］ 高耀东，杨建鸣，汪建新.ANSYS子模型技术的应用［J］.包头钢铁学院学报，2002，21（4）：340-342.

［9］ 蒋友琼.非线性有限元法［M］.北京：北京工业学院出版社，1988.

［10］ 王 磊，李家宝.结构分析的有限差分法［M］.北京：人民交通出版社，1982：10-23.

［11］ 朱合华，陈清军，杨林德.边界元法及其在岩土工程中的应用［M］.上海：同济大学出版社，1997.

［12］ 杨德全，赵忠生.边界元理论及应用［M］.北京：北京理工大学出版社，2001.

［13］ 过镇海.混凝土的强度和本构关系—原理与应用［M］.北京：中国建筑工业出版社，2004.

［14］ 苏礼邦.用子模型方法进行高拱坝预应力闸墩结构有限元分析［D］.西安：西安理工大学，2007：40-68.

［15］ 李 瓒，陈兴华，郑建波，等.混凝土拱坝设计［M］.北京：中国电力出版社，2000：620-621.

Application of Sub-model Method in Stress Analysis of Arch Dam’s Bottom Outlet

GUO Xiao-jing，XU Jin-jin
（Survey and Design Institute，Qiantang River Administration Bureau of Zhejiang Province，Hangzhou，Zhejiang 310016，China）

Here，the finite element sub-modelmethod is applied to the 3D calculation of a high-head and thin arch dam engineering，and the opening stress of the pressure section of its bottom outlet and the stress state of its upstream and downstream cantilevers are analyzed.The results show that the tensile stress of the flow direction of the bottom outlet sidewall in the intersection of upstream cantilevers and dam body is large，but with the traditional plane finite element method，it is considered that this tensile stress is small when calculating the stress near orifices.Then by calculating multiple solutions，the different calculation results of differentmodels are analyzed.Compared with the traditional calculationmethod，using the sub-modelmethod for the analysis of the high-head and thin arch dam’s bottom outletwith finite element analysis could greatly reduce the computational effort and time，and help to improve the accuracy of the calculation.

bottom outlet；upstream and downstream cantilevers；sub-modelmethod；3D finite element

TP311

A

1672—1144（2014）01—0205—04

10.3969／j.issn.1672－1144.2014.01.043

2013-11-10

2013-12-15

郭晓晶（1980—），女，山西襄汾人，硕士，主要从事水利工程方面的设计工作。