离散数学课程考核体系的探索与实践

孙宗剑 陈静

（河北科技大学理学院，河北 石家庄 050018）

离散数学课程考核体系的探索与实践

孙宗剑 陈静

（河北科技大学理学院，河北 石家庄 050018）

本文结合有效教学理念，探索高等学校离散数学课程的考核体系，旨在提高学生们对本课程的学习兴趣，更加有效地提高学生的抽象思维和逻辑推理的能力，促进学生对本课程所学知识的掌握。

有效教学；权重；层次分析法；考核体系

《离散数学》课程是高等学校的必修课，也是数学、软件工程和计算机专业的一门工具基础课。在计算机科学的日益发展下，《离散数学》课程的重要性也越来越明显。它不但给后继课程提供必要的数学方法、数学思想和算法设计，而且通过学习离散数学，能够培养和提高学生们在抽象思维和逻辑推理方面的能力，为学生们今后参加工作或者读研继续学习，从事科学研究打好坚实的数学理论基础。这门课程的概念较多、理论性较强、内容抽象，并且检验该课程的学习标准是以卷面考试为主，较少会辅助有限的实验作为考核。这种传统的考核方式不利于学生们对所需专业知识的掌握，也不利于对学生们的抽象思维能力、逻辑思维能力和专业精神的综合培养。本文以有效教学理论为指导，笔者结合近年来的教学实践，就如何建立新型的《离散数学》考核体系作探讨。

1 《离散数学》课程考核体系的建立

根据有效教学理论，对课程学习的要求使得单一的闭卷考试从考核的中心走近了考核的边缘。根据离散数学的课程特点和教学要求，建立以实验成绩、作业、论文成绩和期末考试等为基本结构的综合考核体系。实验成绩是由实验报告、实验过程和实验结果组成；课内外作业包括教师随堂练习题、布置的课后习题和按照学生们学习程度的不同自主选做的课外习题；论文是由教师按照教学大纲的要求，考虑到学生的个人兴趣，双向选择命题范围，要求学生按照收集资料、阅读参考文献、撰写论文三个步骤进行，教师对论文进行考核时遵照科技论文的指标要求；期末考试试卷的命题按照教学大纲对本课程知识点的要求。这种多元化的综合考核方式可以扩展学生们的知识面，增加实践能力，加强主动学习的意识，更好地掌握本课程的知识。在具体考核时，可以将实验成绩、作业和论文成绩作为本课程的过程考核，将期末考试作为本课程的结果考核。由过程考核了解学生的学习状态，而由结果考核了解学生对知识的掌握情况。

新型的考核体系改变了以往仅仅注重考试成绩的量化考核模式，更加注重培养学生的动手能力，使得传统的单一考核转变为动态化的考核，更加促进学生的全面发展。

2 《离散数学》课程考核因素权重的确定

2.1 层次分析法

在20世纪70年代中期，美国匹兹堡大学的T·L·Saaty教授提出了层次分析法(AHP)。层次分析法将复杂的问题分解成多个因素，再将这些因素按照支配关系分解为目标层、准则层和指标层，然后将这些层次排列起来，形成一个有序的金字塔形的层次结构，建立多目标的数学模型。人们的主观判断通过层次分析法做出形式的表达和客观的描述，通过列出判断矩阵计算相对权重。相对权重的计算指的是通过两两相比这种方式来确定各个因素相对重要性的顺序。为了克服两两相比的不足之处还要对判断矩阵进行一致性检验。

根据《离散数学》课程考核要求，把考核因素划分成a1：实验成绩，a2：作业，a3：论文成绩和a4：期末成绩等四个因素。将各个考核因素进行组合，形成指标间的层次结构，来明确考核因素间的相互关系。权重就是考核因素在考核体系中所占的比重，权重体系就是由考核因素体系中相对应的权重组成的。某一因素的权重指的是该因素在考核过程中的相对重要性，是由不同侧面反映出的该因素的重要程度按照定量进行的分配，这样就可以区别对待课程考核中的各个考核因素的作用。层次分析法可以用来确定课程考核体系中权重系数，其基本思想是通过“两两比较”考核组成的各个因素，将这些因素的整体权重进行组合，然后整个考核体系中各个因素的权重就可以确立了。

2.2 课程考核权重系数的确定

使用层次分析法来确定离散数学课程考核体系中各个因素所占权重的步骤如下：

步骤1：根据给出的四个考核因素，按照各个因素在考核结果的影响重要性来构造出判断矩阵。首先选择因素ai和aj，用aij来表示ai和aj对考核结果影响的比值，然后用判断矩阵A=(aij) n×n表示。而aij的取值按照下述的取值方法给定：取为1，表示两个因素相比，具有同样重要性；取为3，表示两个因素相比，一个因素比另一个因素稍微重要；取为5，表示两个因素相比，一个因素比另一个因素明显重要；取为7，表示两个因素相比，一个因素比另一个因素强烈重要；取为9，表示两个因素相比，一个因素比另一个因素极端重要；取为2、4、6、8，为上述相邻判断的中值。

根据上述取值方法就可以构建离散数学课程考核体系中“考核（A）”的判断矩阵。

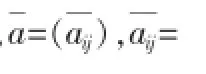
然后经过归一化处理可知，

于是得到“考核（A）”的权重集如所示：

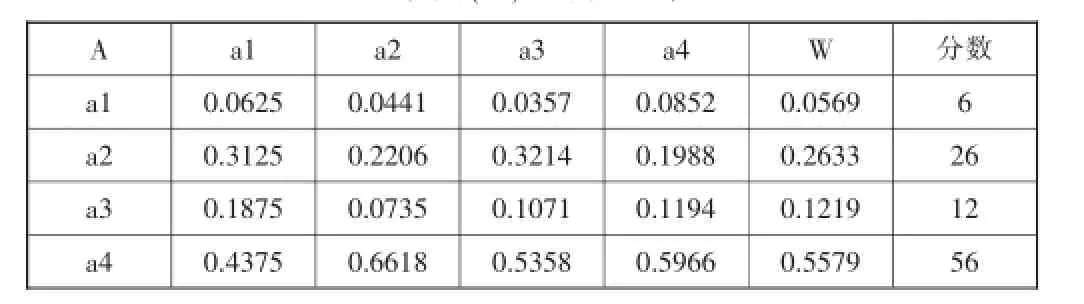
“考核（A）”的权重集

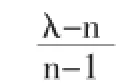
步骤4：形成完整的离散数学课程考核体系。将经过一致性检验后的步骤2中各个考核因素的权重计算得到权重集，该集合反映了各个考核因素在整个考核体系中的重要性。将考核体系中的各个参数值进行整理，用百分制中的整数分数表示“权重”值，这样就可以更直观地反映出考核过程中各个考核因素所占的权重比例，现场操作性比较强，整理后的分数在表1中的“分数”列。

3 离散数学课程考核体系在教学中的实践

在实际教学过程中主要从以下三个方面对离散数学课程的教学方式进行改革。首先，进一步完善教学中的环节，深入研究教材，吃透教材，认真备课；在课堂讲授过程中，要做到概念明确、逻辑清楚、思维缜密。其次，增强实验比重，增强学生动手的机会，增强学习的主动性。再次，建设网络学习平台，方便学生自主学习，充分发挥学生个性，有利于培养学生的创造力和学习能力。

4 结语

本文中的《离散数学》课程考核体系是在有效教学理论的基础上建立的，侧重于对学生的学习能力、学习方法和学习自觉性等方面的综合考核。在课程考核过程中教师要充分运用课程考核的反馈机制，督促学生以考促学，优化课程考核的效果，让学生担任课程考核的参与主体，使学生不再是被动的考试接受者。同时也要明确课程考核不是学生等级划分的手段，课程考核的目的是为了改进教师的教学方法以及促进学生的自我完善。在反馈课程考核结果的同时，难以避免地会存在学生的个体差异，教师要尊重这种差异，找到存在差异的原因及时纠正，更重要地还要关注学生的发展潜能。

[1]康亚明，张烨.网络课程评价体系模型的建立与应用[J].榆林学院学报，2012，11.

[2]赵占山，张静.基于有效教学理念的《离散数学》课程评价体系初探[J].高等职业教育—天津职业大学学报，2012，2.

[3]王瑞胡.应用型本科院校计算机专业《离散数学》实践教学改革研究[J].现代计算机，2010，3.

[4]屈婉玲，王元元，傅彦，张桂芸.离散数学课程教学实施方案[J].中国大学数学，2011，1.

[5]何中圣.离散数学教学中的问题分析与对策研究[J].高等理科教育，2007，5.

G482

A

1003-5168(2014)03-0268-02

河北科技大学理工学院教育教学研究基金资助（2011Y13）。

孙宗剑（1979—），男，山东潍坊人，硕士，讲师，研究方向为组合数学和图论。