河南省规模以上工业企业技术创新差异化研究----------基于Panel Data模型分析

鲁丽萍,焦科研

河南财政税务高等专科学校信息工程系,河南郑州451464

河南省规模以上工业企业技术创新差异化研究
----------基于Panel Data模型分析

鲁丽萍,焦科研

河南财政税务高等专科学校信息工程系,河南郑州451464

从投入-产出的角度，本文研究了我国中部区域河南省各地市规模以上工业企业技术创新的结构差异。首先，利用鸿沟系数从总体上分析规模以上工业企业新产品销售收入比重、R&D人员人均R&D经费、R&D人员占从业人员比重存在的差异；然后，应用Panel Data模型对18个地市规模以上工业企业技术创新投入对产出的结构影响进行深入分析，找出它们之间的结构差异并说明其存在的原因，为各地市企业制定技术创新的发展计划提供参考。

技术创新;鸿沟系数;Panel Data

21世纪是一个知识经济时代，随着经济全球化的深入，创新已经成为国家和企业竞争战略的核心及持续竞争优势的源泉[1]。而技术创新的主体是企业，企业创新能力的高低，不仅影响到自身的生存和发展，也影响到国家竞争力的提升。因此，客观正确地把握企业的技术创新能力是十分必要的。

目前，对企业技术创新能力的研究，国内外学者多是采用综合评价方法。比如，Steele曾经用核对表的形式对R&D活动进行了评价[2]；曹萍，陈富集应用网络层次分析法ANP对企业的技术创新能力进行了评价[3]。钟桦运用数据包络分析方法对不同企业的创新效率进行了评价，针对多个相对有效的企业运用改进的DEA模型进行区分和排序[4]。

综合评价方法大多是对企业的技术创新能力进行整体研究或排名分析，没有明确指出技术创新系统中最为重要的两类指标，即创新投入和创新产出之间的结构关系，无法对企业的技术创新绩效进行准确、有效的评价。因此，本文首先利用鸿沟系数对河南省各地市规模以上工业企业技术创新投入与产出的总体差异进行分析；然后，建立Panel Data模型对河南省各地市规模以上工业企业技术创新投入与产出的结构关系进行深入研究，找出各地市之间存在的差异并分析其中的原因，为各地市企业制定创新发展计划提供参考。

1 技术创新投入与产出的总体差异

1.1 变量的选择

企业进行技术创新，其成果最终体现在生产出市场需要的高技术含量的产品，通过实现销售给企业带来经济收益。因此，企业技术创新成功的标志是，技术促进企业盈利的增长[5]。结合指标选取的原则，从创新活动的投入-产出角度，本文选择规模以上工业企业的新产品销售收入比重（新产品销售收入占主营业务收入的比重）、R&D人员人均R&D经费和R&D人员比重（R&D人员占从业人员的比重）来建立模型。

1.2 投入与产出的鸿沟系数分析

利用鸿沟系数，本文对“十一五”以来规模以上工业企业的新产品销售收入比重、R&D人员人均R&D经费和R&D人员比重进行测度，以衡量河南省各地市规模以上工业企业创新投入与产出的区域总体差异。

如公式（1）所示[6]，新产品销售收入比重的鸿沟系数计算方法是：首先，将各地市企业新产品销售收入的比重进行排序；然后，计算出排名前5位和后5位的地市的平均比重；最后，计算出两者之比，即为新产品销售收入比重的鸿沟系数。该系数越大，说明地市间企业新产品销售收入比重的差距越大。

其中，iIH表示规模以上工业企业新产品销售收入比重最大的5个地市中第i个地市规模以上企业的新产品销售收入；iPH表示规模以上工业企业新产品销售收入比重最大的5个地市中第i个地市企业的产品销售收入；iIL表示规模以上工业企业新产品产出最小的5个地市中第i个地市规模以上企业的新产品销售收入；iPL表示规模以上工业企业新产品产出最小的5个地市中第i个地市规模以上企业的产品销售收入。

因此，公式（1）的分子值表示的是比重最大的5个地市的平均比重，分母值表示的是比重最小的5个地市的平均比重，两者之比表示地市间企业新产品销售收入所占比重的不平衡系数，说明的是地市间规模以上工业企业技术创新产出的差异。

同理，我们计算出各地市规模以上工业企业R&D人员人均R&D经费和R&D人员比重的鸿沟系数，并进一步计算出各指标的平均增长速度，结果如表1～表3所示。

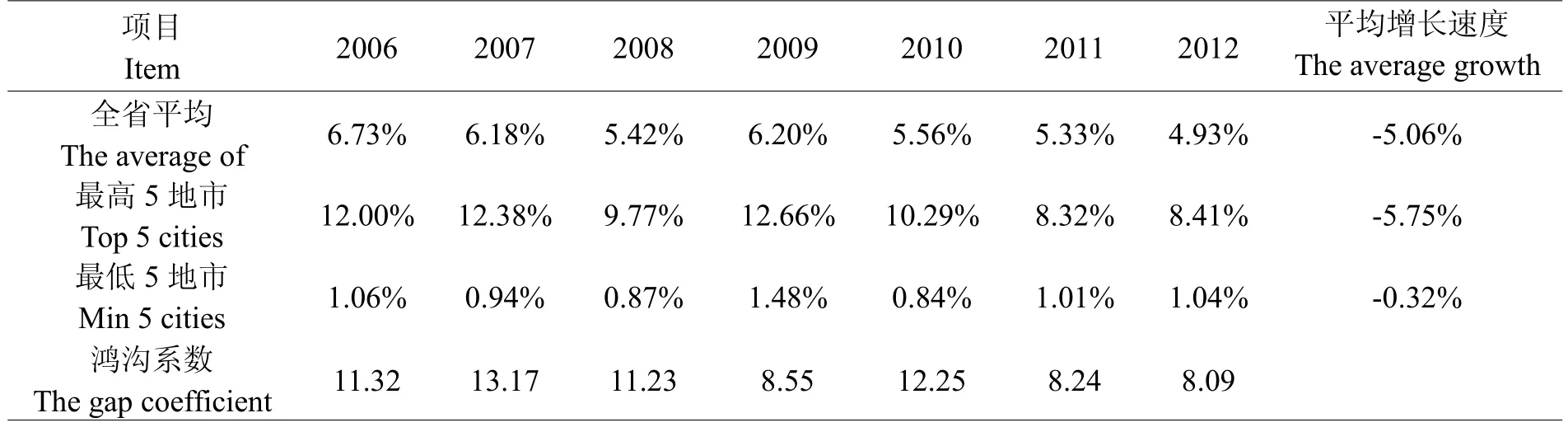
表1 新产品销售收入比重的鸿沟系数Table 1 The gap coefficient of proportion in new product sales revenue

从表1至表3中，我们看到，近几年来，在新产品销售收入比重上，比重最高的5个地市的平均比重约是最低的5个地市平均比重的10.20倍；在R&D经费比重上，比重最高的5个地市的平均比重约是最低的5个地市平均比重的1.97倍；就R&D人员全时当量占企业从业人员比重而言，比重最高的5个地市的平均比重约是最低的5个地市平均比重的4.24倍。这表明：“十一五”以来，河南省规模以上工业企业在3个指标上的确存在较大的地区差异，其中，新产品销售收入比重的地区差距最大。

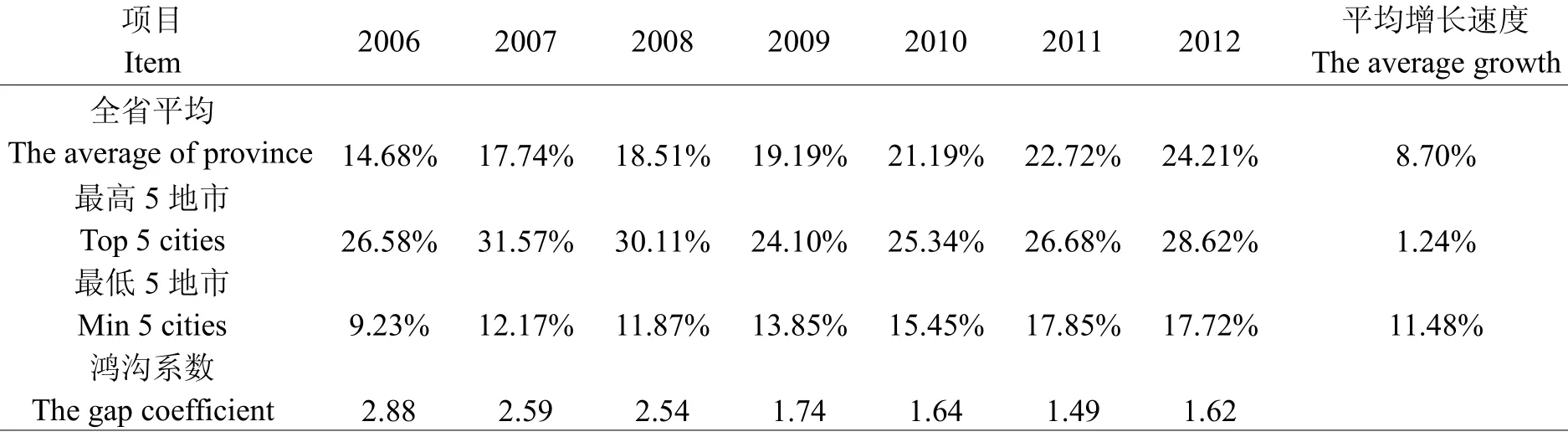
表2 R&D经费内部支出总额的鸿沟系数Table 2 The gap coefficient of total in R&D intramural

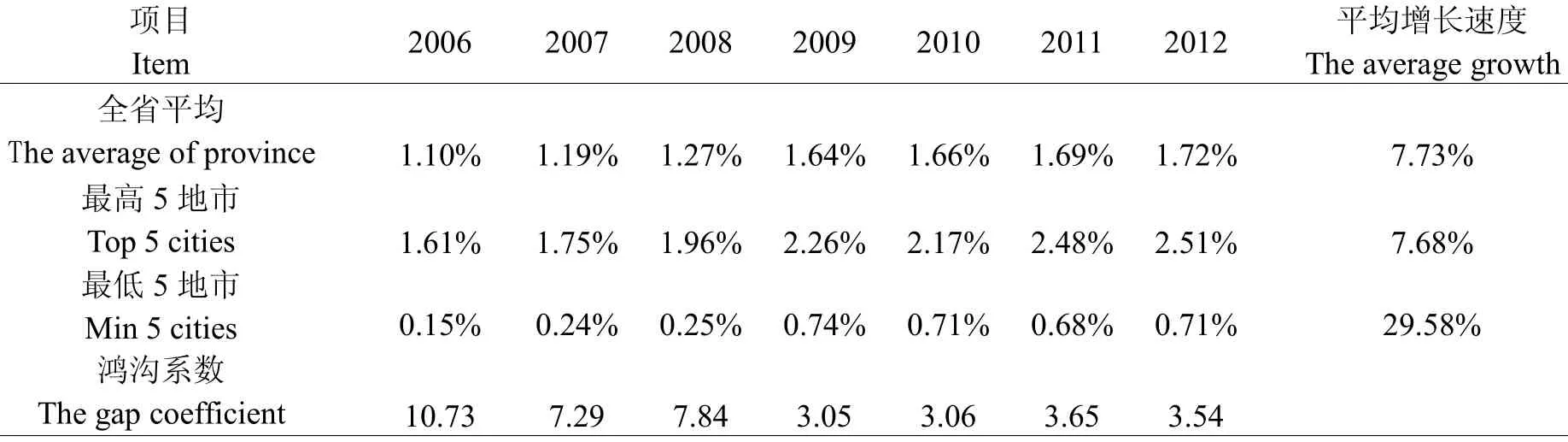
表3 人员全时当量比重的鸿沟系数Table 3 The gap coefficient of proportion in full-time equivalent of staff

从平均增长速度来看，指标值最高的5个地市和最低的5个地市的企业在三个指标上有一定的差异。具体地说，在创新产出方面，即新产品销售收入比重方面，全省比重平均为5.76%，且呈下降趋势；最高5地市的比重平均为10.55%，下降幅度高于全省平均水平；最低5地市的比重变化不大，平均为1.03%，虽有所下降，但下降幅度不大。而在创新的投入方面，即人均R&D经费和R&D人员全时当量占企业从业人员的比重方面，“十一五”以来，全省、比重最高的5地市以及比重最低的5地市的平均比重均有不同幅度的增加，并且，比重最低的5地市平均比重的年均增长速度不仅高于全省水平也高于比重最高的5地市的平均增长速度。这说明，虽然由于企业规模的缘故，指标值最高的5地市和最低的5地市的企业在创新投入和产出方面还是存在着一定的差距，但是，各地市的企业越来越重视技术因素，都在逐步提高技术创新的投入力度，特别是创新能力较弱的地区，企业对技术创新的重视程度越来越大。

2 技术创新投入与产出的结构差异

为进一步深入分析河南省各地市规模以上工业企业技术创新的投入-产出结构，并进而对企业技术创新的绩效进行评价，我们选择规模以上工业企业的新产品销售收入作为被解释变量、R&D经费投入总额和R&D人员总量作为解释变量来建立Panel Data模型，对企业技术创新的投入-产出进行回归分析。

这是因为Panel Data模型是将不同的时间上不同地市规模以上工业企业的技术创新数据作为样本观测值，这样既可以分析不同企业技术创新投入对产出的结构影响,也可以分析企业和政府的相关政策对各地市企业技术创新的影响[7]。而且，Panel Data模型还能够提供更多的信息、更少的共线性、更多的自由度和更大的效率

2.1 模型的选择

根据C-D生产函数，本文建立的反映企业技术创新投入与产出结构关系的模型为：

其中，Y表示的是规模以上工业企业的新产品销售收入；A可视为效率参数，A的数值越大，既定投入要素所能得到的创新产出也越大；K表示的是规模以上工业企业的R&D经费；L表示的规模以上工业企业的R&D人员。对（2）式两边取自然对数，得到模型：

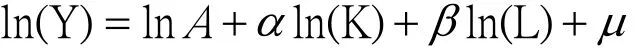
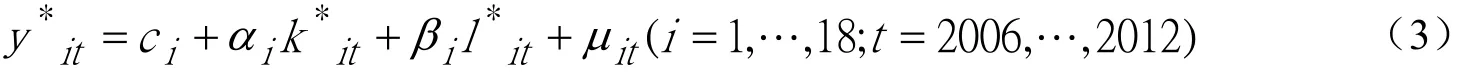
其中，系数αi和βi分别表示河南省的18个地市中，第i地市规模以上工业企业的R&D人员和R&D经费的投入产出弹性系数。

要采用Panel Data模型对模型（3）进行回归分析，首先要通过F检验以确定Panel Data模型的具体形式。Panel Data模型的具体形式主要有三种：

①固定系数模型

在横截面上无个体影响、无结构变化,则普通最小二乘估计给出了α和β的一致有效估计，相当于将多个时期的截面数据放在一起作为样本数据。

②变截距模型

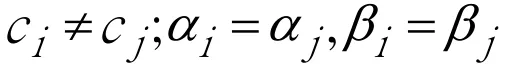
在横截面上个体影响不同,个体影响表现为模型中被忽略的反映个体差异的变量的影响，又分为固定影响和随机影响两种情况。

③变系数模型

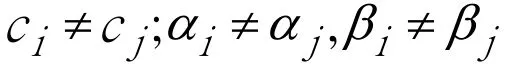
该模型中除了存在个体影响外,在横截面上还存在变化的经济结构,因而结构参数在不同横截面单位上是不同的。典型的Panel Data模型是横截面单位较多而时期较少的数据[7,8]。

检验模型（3）应采用上述3种类型中的哪一种，目前广泛使用的是协方差分析检验，主要检验两个假设：

假设1：斜率在不同的截面样本点和时间点上都相同，但截距不相同。

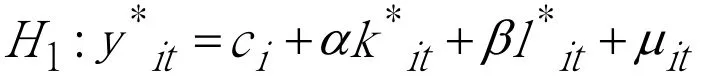
假设2：截距和斜率在不同的横截面样本点和时间上都相同。

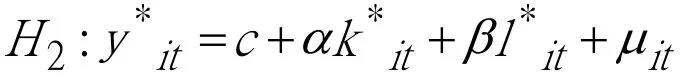
对上述假设进行检验时，首先需要构造两个统计量1F,2F：

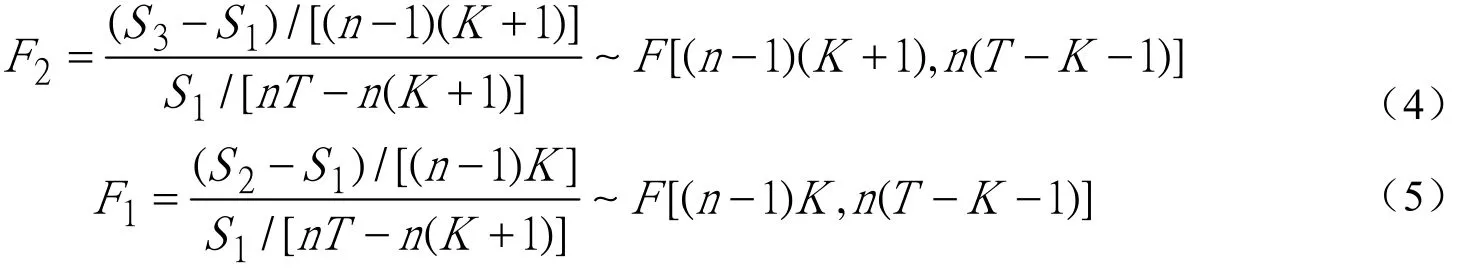
在对模型进行识别过程中，若F2小于临界值则接受假设2，选择模型③；否则拒绝假设2。当假设2被拒绝后，再检验假设1，若F1小于临界值，则接受假设1，即选择模型②；否则拒绝假设1，选择模型①[8]。

根据“十一五”以来，即2006年至2012年河南省各地市规模以上工业企业的创新数据，两个统计量F1，F2中的n的取值为18，K的值为2，T为7。使用Eviews软件，计算得到情形3模型的残差平方和S1=98.97，情形2模型的残差平方和S2=146.45，情形1模型的残差平方和S3=258.52，根据公式（4）和（5）的检验H1和H2的F统计量，我们可以计算出F1=1.03，F2=2.77，大于α=5%的F2临界值但小于α=5%的F1临界值，故拒绝假设2，接受假设1，采用情形2的模型形式，即斜率在不同的截面样本点和时间点上都相同，但截距不相同。

进一步地，根据模型分为固定效应和随机效应两种，结合本文的具体情况，即选取了全部的截面单位，故选择固定效应。

2.2 模型的估计

由于存在多个截面个体，为减少异方差的影响，本文采用的是加权最小二乘法。使用Eviews软件计算结果如下：

表4 各地市的截距Table 4 Intercept around the city

表5 R&D人员变量与R&D经费变量的系数Table 5 The coefficients of R&D personnel variables and R&D expenditure variables

估计方程为：

另外，模型的R2 =0.9991，DW..=1.9588，F=131759.2000，由F检验值可说明模型总体上显著成立，R2接近于1说明模型拟合的效果也非常好。并且，DW..=1.9588，经查表在α=5%的情况下，DW..∈(du,4-du)，因此，该模型不存在自相关。

2.3 回归结果分析

根据Eviews软件，我们得到的估计方程是Panel Data模型中的第二种类型，即变截距模型。这说明：河南省各地市之间存在着个体差异，表现为它们的截距不同，但由于18个地市在地理位置上较靠近，经济和工业发展水平相对较接近，因此，各地市的经济结构没有大的变化，表现为估计方程中两个解释变量的系数相同。

方程（6）中的截距项ci(i=1,2,...,18)可视为河南省各地市的效率参数，其数值越大，既定创新投入要素所能得到的创新产出也越大，它代表的实际上是新产品产出中不能被两大投入要素数量增长所解释的那部分。根据本文所选择的投入要素，即R&D人员以及R&D经费，再全面结合影响企业技术创新的因素来分析，这部分内容包括了新技术的水平、企业的组织管理水平以及技术基础设施等综合因素。根据表4，我们得到在河南省的18个地市中，南阳、洛阳、新乡、平顶山这些发展较好的地市，效率都较大，位居全省前列；信阳、鹤壁、三门峡、商丘、濮阳这些工业发展较慢的地市，效率位于全省的后5位；其余地市规模以上工业企业的效率位居全省中游水平。

ln()K的系数表示的是河南省规模以上企业R&D经费的投入产出弹性系数，反映了R&D经费投入对创新产出的影响效果，表5显示，该系数为0.96。这说明R&D经费对新产品产出产生正的作用。ln(L)的系数表示的是河南省规模以上工业企业R&D人员的投入产出弹性系数，反映了R&D人员的投入对创新产出的影响效果，然而，根据表5，该系数为0.03。这个数字本身说明R&D人员对创新产出的影响较小，但从它的t检验值来看，实际上该系数没有通过t检验，也就是说R&D人员对创新产出的影响不显著。总的来说，河南省规模以上工业企业的创新产出受R&D经费的影响较大，但受R&D人员的影响不大。这主要是源于河南省规模以上工业企业R&D人员的整体素质不高，R&D人员中研发能力较强的优秀人才不多，河南省规模以上工业企业整体的研发能力不强，导致R&D人员对企业创新产出的影响相对较小。根据统计数据，河南省规模以上工业企业R&D人员中高素质人员的比重基本上都位居中下游水平。

3 结论

通过以上的分析，我们可以看出：

（1）总的来说，河南省规模以上工业企业R&D人员整体素质不高导致企业的R&D人员对企业创新产出的影响不显著。因此，河南省规模以上工业企业应建立更有效的创新人才引进、培养以及激励机制。我们认为：①通过较高的报酬或优越的工作条件引进高素质的创新人才。②对企业有潜力的研发人员提供再学习的机会，提高企业现有创新人才的素质，增强其创新能力。③完善企业的组织管理水平，完善企业创新人员的激励机制，更有效地调动企业研发人员的创新积极性，提高企业创新成果的数量和质量。例如，企业可以对取得高质量研发成果的R&D人员以一定的物质奖励。同时，也可以将其和职务相联系，将研发成果作为职务或职称评定的一项重要指标以激发R&D人员的创新积极性。此外，各级政府应根据当地的技术发展水平进一步完善专利保护制度，保护创新者的利益和积极性。④加强产、学、研的结合，实现社会人才的共享。各地区的R&D人员有相当一部分分布在科研机构和高等院校，因此，企业应进一步注重产学研的合作，进行协同创新，从而实现社会科技人才资源的充分利用，并有效提高企业研发的成功率。

（2）具体地说，工业发展较慢的地市，比如：信阳、鹤壁、三门峡、商丘、濮阳等，其创新投入-产出的效率较低。因此，这些地市应首先提高对创新产出影响大的指标，即R&D经费的投入力度，然后，再逐步地完善企业创新人才的引进、培养以及激励机制，提高R&D人员的素质，提升企业的自主创新能力。而对于工业发展较快、创新能力较强的地市，比如：洛阳、新乡、郑州、平顶山、南阳等，其创新积极性较高，因此，这些地市在保持R&D经费投入力度的情况下，应进一步提高R&D人员的素质，增强企业的自主创新能力，进一步提高企业创新产出效率。

[1]陈伟.创新管理[M].北京:科学出版社,1996

[2]Steele L W.Evaluating the Technical Operation[J].Research Management,1988,31(5):11-18

[3]曹萍,陈富集.基于ANP理论的企业技术创新能力评价模型[J].科学学与科学技术管理,2010(2):67-72

[4]钟桦.DEA改进模型的企业技术创新能力评价[J].系统科学学报,2010,18(4):86-90

[5]王同律,王季云.企业技术创新管理[M].北京:中国标准出版社,2003

[6]俞立平,周曙动.我国地区教育经费投入差距——基于PanelData的变系数模型研究[J].社会科学研究,2006(2):23-27

[7]叶阿忠.平行数据模型的设定和估计[J].合肥工业大学学报(自然科学版),2002(4):248-251

[8]李子奈,叶阿忠.高等计量经济学[M].北京:清华大学出版社,2002

Study on the Differentiation of Technological Innovation from Industrial Enterprises above Designated Size in Henan Province of China----------Based on Panel Data model analysis

LU Li-ping,JIAO Ke-yan
Department of Information Engineering,Henan College of Finance&Taxation,Zhengzhou 451464,China

The paper researched the regional differentiation of technological innovation of industrial enterprises above designated size in Henan Province from the angle of input-output.Firstly,dividing coefficient is applied to analyze the regional differentiation of the revenue from the sale of new products,the intramural expenditure on R&D activities and the R&D personnel of industrial enterprises above designated size in Henan Province as a whole.Then,using the panel data model,the paper thoroughly analyzed the structural influence of technological innovation from input to output of 18 prefecture-cities in Henan Province,and found out the structural differentiation and explained the cause.In conclusion,the paper will put forward some pertinent measures to improve technological innovation ability of industrial enterprises above designated size of each prefecture-city in Henan Province.

Technological innovation;dividing coefficient;Panel Data

O212

A

1000-2324(2014)03-0463-06

2012-12-25

2013-02-24

河南省软科学计划项目(142400410834);河南省软科学计划项目(142400410274)

鲁丽萍(1963-),女,副教授,河南开封人,本科,研究方向:经济数学与经济统计等.