基于最大最小蚁群算法的智能装载方法

葛玮,徐卫红,程海水

江西广播电视大学,江西南昌330000

基于最大最小蚁群算法的智能装载方法

葛玮,徐卫红,程海水

江西广播电视大学,江西南昌330000

三维装箱问题在现实生活中有着广泛的应用，是具有复杂约束的组合优化问题，理论上属于NP-hard问题。针对贪心算法通常得到的是局部最优解以及基本蚁群算法存在不足等问题，本文首先给出了启发式装箱规则，然后结合最大最小蚁群算法对装载顺序进行优化，提出了一个求解三维装箱问题的混合蚁群算法，最后通过实验对比验证了该算法的有效性和优越性，并给出了三维效果展示图。

三维装箱;启发式;最大最小蚁群算法

装箱问题在现实生活中具有广泛应用，如切割加工业和运输业。高利用率的切割和装载可以节约大量成本。实际应用中由于不同的优化目标和装载约束，导致了不同种类的装箱问题。Dyckhoff和Finke概述了不同类型的装箱问题[1]。本文所处理的三维装箱问题是其中之一。

三维装箱问题是具有复杂约束条件的组合优化问题，理论上属于NP-hard问题[2]，采用精确求解算法是不现实的，因此启发式求解方法成为理论研究和实际应用的首选。Ngoi[3]以及Bischoff[4]等提出了一些启发式算法。Gehring[5]等将遗传算法应用到装箱问题中。Bortfeldt[6]等分别提出了禁忌搜索求解算法、混合遗传求解算法和基于分支定界的一个启发式算法。Moura等提出了一个随机自适应启发式算法GRASP[7].国内学者在三维装箱问题的研究上，也取得了不错的成果[8-14]，特别是黄文奇等提出了一种最大穴度的占角动作优先的拟人型求解算法[13]，张德富等将启发式算法和模拟退火算法相结合，提出了混合求解算法[14]。通过对上述文献的研究分析，发现启发式算法和一些智能算法以及二者的结合对解决三维装箱问题很有效果。

本文采用最大最小蚁群算法结合启发式算法对其进行优化，提出了一个有效的求解三维装箱问题的混合算法，克服了传统贪心算法容易陷入局部最优值的不足。

1 问题描述

本文探讨的三维装箱问题的形式化定义：给定一个长方体容器C和一个待装箱的长方体箱子集合B={b1,...,bn}，容器C的长宽高分别为L, W, H，最大载重量Z，为每个箱子bi的长宽高为li, wi, hi，重量为zi。设S为B的一个子集，问题的目标是确定一个可行的放置箱子的方案，即选择B的一个合适的子集S使得满足给定约束的情况下，容器的空间利用率最大，即

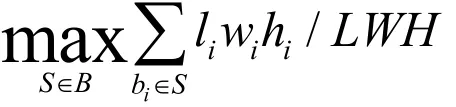
放置方案要求满足如下7个条件：

(1)被装载的箱子必须完全被包含在容器中；

(2)任何两个被装载的箱子不能相互重叠；

（3）所有被装载的箱子的摆放方向与容器的三维保持正交；

（4）方向约束C1：分为任意翻转和水平旋转两种；

（5）容器最大承重约束C2：装载完成后，货物的总重量不得超过容器的最大限重；

（6）稳定性约束C3：每个被装载的箱子必须得到容器底部或者其他箱子的支撑，也就是说禁止被装载的箱子悬空；

（7）承压约束C4：本文只考虑0～1承压约束，即该箱子上可放置(1)或不可放置(0)其他箱子。

2 基于最大最小蚁群算法的智能装载方法

2.1 启发式装箱算法

2.1.1 空间分解本文对容器布局空间的分解过程采用单链表数据结构表示。首先对原始布局空间求解，此时，原始布局空间为容器的内部空间，单链表中只有一项，包含该空间的左后下角的三维坐标(0,0,0)以及容器长宽高的值。然后按照某一装载顺序，从可选待装载箱子中选择一个箱子，在链表中从表头开始查找一块可装下该箱子的空间并将其定位于当前布局空间左后下角，如图1位置所示。由图可知，箱子将原空间划分为前空间fronts，右空间rights和上空间ups，将这三个空间按序插入到链表中，并删除原空间，从可选待装载箱子集合中删除该箱子。对这三个布局空间依次重复上述过程，直至所有箱子装载完成或容器已没有可利用空间。

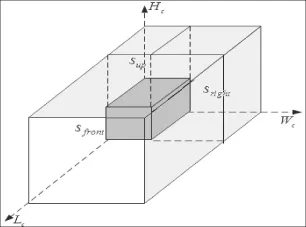
图1 空间划分示意图Fig.1 Schematic diagram of space division

2.1.2 剩余空间合并剩余空间指待装填的空间。在算法初始阶段，剩余空间是整个集装箱。随着上节的空间分解，剩余空间越来越多，体积越来越小，会产生一些不能装入任何箱子的剩余空间。如果能将这些较小的剩余空间尽量与其他剩余空间进行合并，则可大大提高空间利用率。剩余空间合并的算法细化如下：

假设待插入链表的空间为s，剩余空间链表S={si}，算法的具体流程如下图2所示。

2.1.3 算法规则首先根据待装载的箱子集合B={b1,...,bn }得到一个序列p={P1, P2,...,Pn }，Pi∈[1,n]且为整数，其值代表箱子的编号，按这个顺序进行装填。整体的算法流程如下：

1初始化：剩余空间链表S，表中只有一项s0，即容器的内部空间，左后下角坐标为(0,0,0)，

图2 剩余空间合并算法流程图Fig.2 The remaining space merging algorithm flow chart

长宽高为容器的长宽高(,,L W H)；箱子集合B中所有箱子的状态标记isLoaded=false。

返回容器C最终的空间利用率。

2.2 基于最大最小蚁群算法的装载算法

2.2.1 蚁群算法蚁群算法是一种模拟进化算法，利用蚁群在搜索食物源的过程中体现出的寻优能力解决一些离散系统优化中的问题。蚁群算法不需要任何先验知识，最初只是随机地选择搜索路径，随着对解空间的“了解”，搜索变得有规律，逐渐逼近从而最终到达全局最优解。对解空间的“了解”

主要表现两个方面：①蚂蚁之间利用信息素相互通信：蚂蚁在所选择的路径上会释放一种称为信息素的物质，当蚂蚁选择路径时，会根据路径上残留的信息素进行选择；②群体智能：通过一只蚂蚁的运动很难找到食物源，但整个蚁群进行搜索一般就能找到。当某些路径上的信息素量越来越多，蚂蚁选择该路径的概率随之增加，进而又增加了该路径上的信息素强度。同时所有路径上的信息素随时间而蒸发。模拟这种现象即可利用群体智能建立寻优机制，使蚁群算法的搜索向最优解推进。本文采用的最大最小蚁群算法是改进的蚁群算法，比基本的蚁群算法的寻优效果更佳。

2.2.2 混合蚁群算法的启发式装装载方法1）编码编码是把一个问题的可行解从其解空间转换到蚁群算法所能处理的搜索空间操作。本文将待装载箱子的编号按某一装载顺序编成串作为一个解的编码，也是一条路径，即

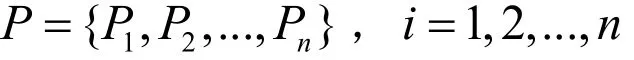
式中：n为待装载的箱子的个数；iP为整数，其值代表箱子的编号。简单地，可以根据箱子的体积从大到小排序，即贪心策略得到序列p，是可行解集合中的一个。

通过信息素对串P进行操作实际上就是改变待装载箱子的装载顺序，从而可以产生不同的解序列。

2）信息素与路径选择概率蚁群觅食时，信息素浓度越大的路径总长度越短。对于三维装箱来说，可以用适应度函数来评价一个解的好坏，适应度值越大，解的质量越高。本文的适应度函数f取容器的空间利用率，。路径上的信息素更新满足如下公式：

其中，ρ为信息素残留因子（1-ρ为信息素挥发因子），Δτbest=1/f( Sbest)，f( Sbest)为全局最

ij优路径或局部最优路径的适应度值。本文采用的最大最小蚁群算法，路径上的信息素浓度，最大信息素阈值取适应度，即maxbestfτ=，最小信息素阈值其中参数bestp一般取0.5，n为待装载箱子的数量。

路径选择概率：在运动过程中，第k只蚂蚁根据各条路径上的信息素浓度决定转移方向，即第k只蚂蚁在i节点时选择下一个节点j的概率为

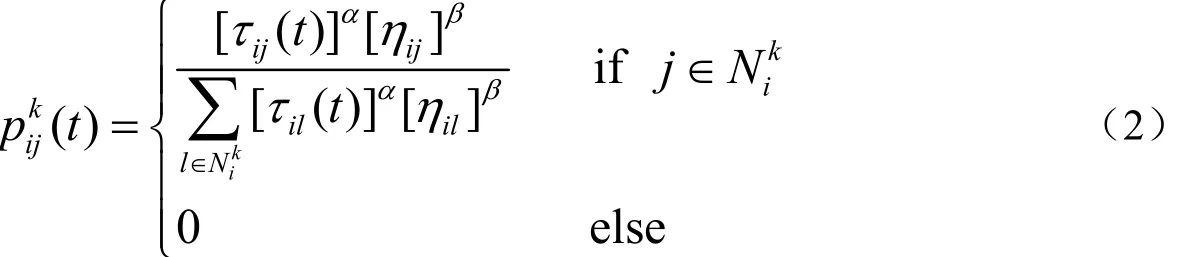
其中，ijη为期望启发信息，这里选取箱子i与箱子j占容器C总体积的比值差的倒数；α为信息素启发式因子，β为期望启发式因子。

3）算法流程

本文提出混合蚁群算法是先采用蚁群算法得到一个初始的装箱顺序，然后再调用启发式算法解码，原装箱顺序可能因为约束等因素会有所改变，信息素是根据解码后实际的装箱顺序来更新的，具体如下：

步骤1：初始化参数，设定迭代次数ncmax，nc，蚂蚁数量m，α、β的值，初始化信息素启发表τij(0)，计算启发式信息表ηij。

步骤2：将蚂蚁k( k=1,2,...,m)的初始出发点置于当前解集中（初始解集为空），由式（2）的概率pk(t)计算蚂蚁k，移至下一结点，将结点j加入当前解集，最后得出一组编码P，ij即一个装箱顺序。

步骤3：调用启发式算法对编码进行译码，实际装箱顺序可能会有所改变，记为P'，计算各蚂蚁走完完整路径后得到的适应度值，记录当前最好的解P'best。

步骤4：按式（1）更新路径上的信息素。

步骤5：nc＜--nc+1。若nc＜ncmax，则返回步骤（2）。

步骤6：输出当前最优解。

3 实验对比及结果展示

假设待布局的容器为国际标准的集装箱，尺寸为2.352 m×2.388 m×5.899 m，最大承载质量为18.07 t[9]。首先根据文献[4]中随机产生箱子的方法，与第3节中基于贪心算法的简单启发式算法进行比较实验。箱子的种类为8种，每个箱子ib的尺寸满足：0.05 L＜li＜0.5 L，0.05 W＜wi＜0.5W，0.05 H＜hi＜0.5 H；重量约束满足：zi＜0.05 Z。在满足约束C1（可任意翻转）、C2、C3和C4（可放置）的条件下，50组随机数据实验的平均结果为：混合蚁群算法空间利用概率为83.92%，基于贪心算法的简单启发式算法空间利用概率为75.68%。混合蚁群算法的结果明显优于启发式算法，并且发现箱体尺寸越小，数目越多，混合蚁群算法的结果越好，启发式算法结果越差。

另外将本文混合蚁群算法与文献[10]中采用基本蚁群算法进行了比较实验，满足约束C1（可任意翻转）、C2、C3和C4（可放置）。待装载的箱子数据参见文献[10]中的表1，箱子数量为30。蚁群算法的参数设置：ncmax=50，m=30，α=1，β=5，ρ=0.95。运行10次的平均结果如下：本文算法的空间利用率为85.67%，文献[10]中采用基本蚁群算法得到的空间利用率为84.09%，简单启发式算法的空间利用率只有82.28%。相比之本文算法效果更佳，速度跟文献[10]中的算法差不多。下表1是本文算法的最好结果。

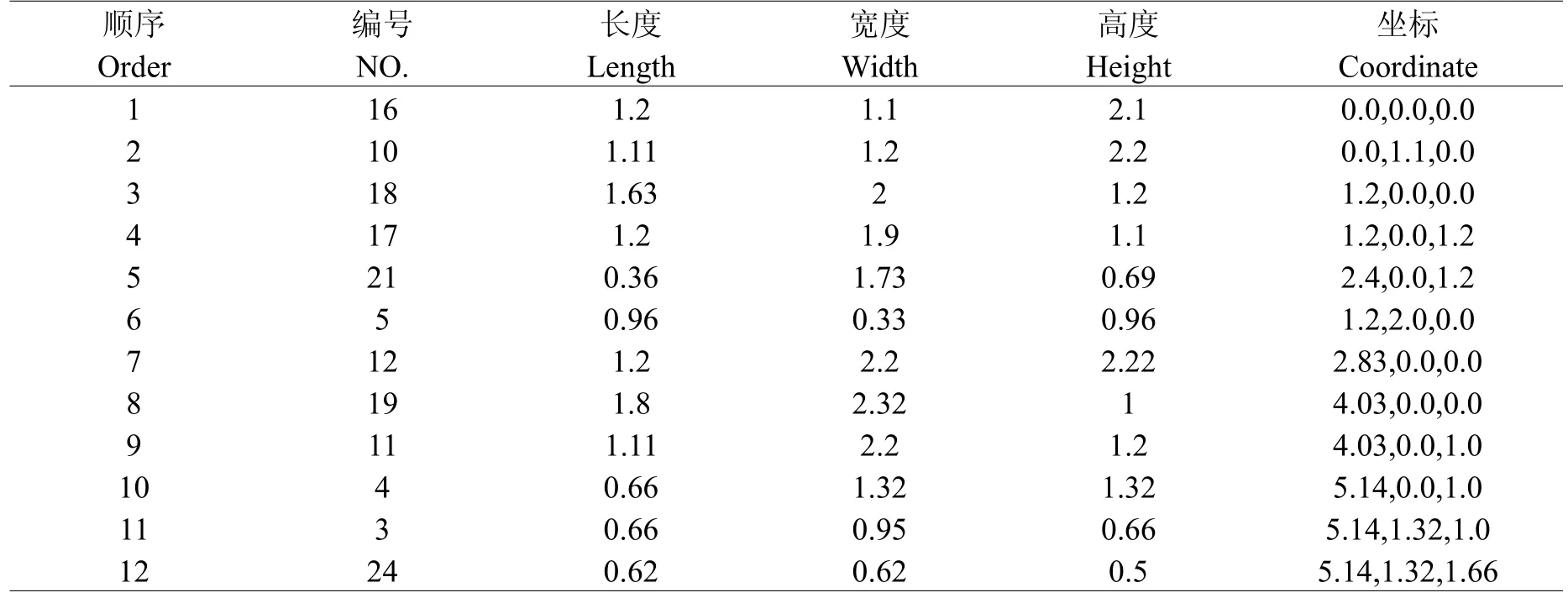
表1 装箱测试结果Table1 Loading test results

在x3dom网上开放源代码的基础上，制作了一个可以展示三维装箱的html网页，表1的装箱测试结果的三维展示效果图如图3所示。

4 总结

通过对大量三维装箱方面文献的阅读和研究分析，发现将智能算法和启发式算法结合对解决三维装箱问题很有效果。因此，本文将最大最小蚁群算法与启发式规则相结合，提出了一个解决三维装箱问题的混合蚁群算法。通过实验对比，验证了该算法的优越性。

本文优化算法采用的是最大最小蚁群算法，对参数值的大小依赖很高，今后的研究可以考虑改进最大最小蚁群算法，使其更好地与三维装箱问题相结合；还可以考虑换成其他更新更先进的智能算法，可能会得到更好的解。本文只研究了单一容器的三维装箱问题，今后可以考虑在此基础上研究多容器的装箱问题。

图4 表1中装箱结果的三维展示Fig.4 Three dimensional display cases results in table 1

[1]Guntram Scheithauer.Algorithms for the Container Loading Problem[J].Operations Research Proceedings,1992,1991:445 -452

[2]Johnson D S.计算机和难解性—NP完全性理论导论[M].张立昂译.北京:科学出版社,1990

[3]Ngoi BKA,Tay ML,Chua ES.Applying spatial representation techniques to the container packing problem[J]. International Journal of Production Research,1994,32(1):111-123

[4]Bisehoff E E,Ratcliff B S W.Issues in the development of approaches to container loading[J].Omega,1995, 23(4):377-390

[5]Gehring H,Bortfeldt A.A genetic algorithm for solving the container loading problem[J].International Transactions in Operational Research,1997,4(5-6):401-418

[6]Bortfeldt A,Gehring H.A hybrid genetic algorithm for the container loading problem[J].European Journal of Operational Research,2001,13l(1):143-161

[7]MouraA,Oliveira J F.AGRASP approach to the container loading problem[J].IEEE Intelligent,2005,20(4):50-57

[8]李广强,滕弘飞.装填布局的同构和非同构模式[J].计算机学报,2003,10:1248-1254

[9]陈建岭.集装箱装载问题的启发式优化算法[J].山东交通学院学报,2005,13(3):53-56

[10]庄凤庭,张磊,张春鲜,等.基于蚁群算法的集装箱装载问题[J].江南大学学报(自然科学版),2007,12(6):795-799

[11]张德富,魏丽军,陈青山,等.三维装箱问题的组合启发式算法[J].软件学报,2007,18(9):2083-2089

[12]宁爱兵,熊小华,马良.城市物流配送中的三维装箱算法[J].计算机工程与应用,2009,45(9):207-211

[13]Huang Wen-Qi,He Kun.A caving degree approach for the single container loading problem[J].European Journal of Operational Research,2009,196(1):93-101

[14]张德富,彭煜,朱文兴,等.求解三维装箱问题的混合模拟退火算法[J].计算机学报,2009,32(11):2147-2156

[15]蓝启明,张东站.公路物流智能配载的研究和装载算法设计[J].计算机工程与应用,2012,48(33):237-243

[16]吴楚楠,刘科峰,彭斯俊,等.大规模集装箱装载问题[J].计算机工程与应用,2013,49(1):231-233,257

Intelligent Loading Methods Based on Max-min Ant Colony Algorithm

GE Wei,XU Wei-hong,CHENG Hai-shui
Jiangxi Radio&TV University,Nanchang 330000,China

Three dimensional container loading problem in real life has a wide range of applications,and it is a combination of complex constrained optimization problems belong to NP-hard in the theory.For the greedy algorithm usually to get a local optimal solution and the basic ant colony algorithm deficiencies and other issues.Firstly this paper gave a Heuristics boxing rules,and then combined the max-min ant colony optimization algorithm to optimize the loading sequence and proposed to solve a three-dimensional hybrid ant colony algorithm for bin packing problem.Finally validated by experiments comparing the effectiveness and superiority of the algorithm,and gave a figure of three-dimensional demonstration.

Three dimensional container loading problem;heuristics;max-min ant colony algorithm

TP18

A

1000-2324(2014)03-0366-06

2013-03-11

2013-04-25

江西省教育厅发展规划课题(JXJG-13-71-4)

葛玮(1981-),男,硕士,讲师,主要从事智能计算机研究.