物候模型在北京观赏植物开花期预测中的适用性

张爱英王焕炯戴君虎丁德平

1）（北京市气象服务中心，北京100089）

2）（中国科学院地理科学与资源研究所，北京100101）3）（中国科学院大学，北京100049）

物候模型在北京观赏植物开花期预测中的适用性

张爱英1）*王焕炯2）3）戴君虎2）丁德平1）

1）（北京市气象服务中心，北京100089）

2）（中国科学院地理科学与资源研究所，北京100101）3）（中国科学院大学，北京100049）

以北京地区玉渊潭公园杭州早樱（1998—2012年）、密云农业气象试验站白玉兰（1996—2012年）及颐和园公园山桃（1981—2012年）物候观测资料和海淀、密云气象站的1981—2012年逐日平均气温观测资料为基础，分别应用国际通用的3种物候模型（SW模型、UniChill模型和统计模型）对以上植物的始花期和盛花期建模，并评估模型适用性。结果表明：SW模型在北京地区3种观赏植物开花期预测中适用性最高，其交叉检验的均方根误差仅为1.93～3.58 d，其次为 UniChill模型（均方根误差为2.49～3.79 d），统计模型效果最差（均方根误差为2.36～4.24 d）。因此，推荐在观赏植物开花期预测业务中采用SW模型。

物候模型；开花期；预测；适用性

引 言

近年来，观赏植物的开花期预测已经成为倍受关注的焦点问题之一，准确预测观赏植物开花期可为公众出游安排提供必要的指导。

物候模型是预测观赏植物开花期的有效方法。物候模型是基于植物对环境因子的响应机理而建立的可模拟植物生长发育的数学模型［1-2］。国内外许多学者建立了多种类型的物候模型［3-16］，这些模型被归纳为静态模型（也称统计模型［13］）和动态模型（也称过程模型［13］）。动态模型是通过数学方法再现生物过程与环境的关系，试图从机制上探讨物候期发生条件的模型［15］。在动态模型中，较为通用的是基于积温理论的春暖模型（Spring Warming Model，SW模型）或热时模型（Thermal Time Model）［12］。SW模型是较为简单的物候模型之一，被广泛用于不同地域植物物候期的模拟研究；另一种更为复杂的动态物候模型由 Chuine［7］提出，称为UniChill模型。截至目前，物候模型已被成功地用于重建过去气候变化［13-14］、预测树种分布范围变化［16］、预测21世纪的物候变化［17］以及植物灾害风险评估等方面［18］。与动态物候模型相比，静态模型则是直接利用统计方法拟合物候期与气候因子关系来建立的物候模型。

长期以来，物候模型较多应用于农业生产领域。李荣平等［19］检验了4种模型在作物发育期模拟中的效果，为作物发育期预报业务提供了理论依据；张谷丰等［20］将物候模型应用在水稻纵卷叶螟发生期的预测中，取得了初步成效。在观赏植物物候期预测方面，国内学者多利用物候期与气象因子的关系，建立静态物候模型进行预测［21-26］。总体来看，动态物候模型在观赏植物物候期预测方面的应用还较少。

本文分别采用两种动态物候模型（SW模型、UniChill模型）和一种静态物候模型（统计模型），建立北京地区3种特色观赏植物（玉渊潭公园杭州早樱、密云农业气象试验站的白玉兰、颐和园公园的山桃）始花期和盛花期模拟模型。在此基础上，对各模型的模拟和预测效果进行检验，评估3种模型在北京观赏植物开花期预测中的准确性，并遴选出最为适用的模型。本研究结果可为北京春季观赏植物开花期预测提供一种可行的方法。

1 资料及处理

1.1 物候资料

本文所用的物候资料为北京地区玉渊潭公园的杭州早樱（Prunus discoidea）、密云农业气象试验站的白玉兰（Magnolia denudata）和颐和园公园的山桃（Amygdalus davidiana）始花期和盛花期长序列物候观测资料。观测资料起止时间和来源列于表1。根据中国物候观测网的观测标准：始花期定义为观测植株上开始出现第1个完全开放的花朵的日期；盛花期定义为观测的树木上有一半以上的花蕾都展开花瓣的日期。

表1 本研究所采用观赏植物及物候资料一览表Table 1 Phenological data used in this study

1.2 气象资料

本文所用气象资料来源于北京市气象信息中心，包括海淀和密云气象站的1981—2012年逐日平均气温资料序列，所有资料均通过了严格的质量控制。图1给出3个物候观测站点（玉渊潭公园、颐和园公园和密云农业气象试验站）和2个气象观测站点在北京地区的位置图。颐和园公园和海淀气象站地理位置非常靠近，密云农业气象试验站和密云气象观测站为相同的地理位置。而玉渊潭公园虽与海淀气象站有一定距离，但已是本文能获得的最近处的气象资料。因此，本文模拟玉渊潭公园杭州早樱、颐和园公园山桃开花期所用的气象资料为海淀气象站资料，模拟密云白玉兰开花期所用的气象资料为密云站资料。

图1 本研究所用物候观测站和对应的气象站位置Fig.1 Location of phenological and meteorological stations

2 方 法

2.1 模型简介

2.1.1 SW 模型

SW 模型基于积温理论发展而来［8，11］，是 最简单的物候模型之一，包括t0，Tb和G3个参数，如式（1）和式（2）所示：

其中，y是预测的植物物候期（日序），xt是第t日的日平均气温；D（xt）是高于某一界限温度值的累积温度，简称积温，代表了植物的发育进程。Tb是界限温度，祝廷成等［27］指出一般植物在0～35℃的温度范围内，随温度上升，生长迅速，随温度降低，生长缓慢，即Tb一般在0～35℃之间。t0是积温开始累积的时间，通常以日序来表示，例如，t0为28是指当年的1月28日。G指完成发育所需的积温阈值。

2.1.2 UniChill模型

UniChill模型［7］考虑了植物芽发育过程的两个阶段，即休眠期和静止期。休眠期是指即使在有利的外界条件下，植物的发育和细胞生长仍被内在因子抑制的时期［24］。休眠期只有通过一定时间的低温刺激才能到静止期。静止期是休眠期打破后，发育和生长受到外界因子（通常是气温）驱动的时期。其公式如下：

其中，t1为开始累积冷积单元的时间，设定为前一年的9月1日。该模型包括a，d，e，k，l，C和G7个参数。参数a，d和e确定了低温促使休眠期打破的过程中，冷激速度对日平均气温的响应函数Rc（xt）（也称冷激单元，chilling units）。Sc是冷激单元的累积和，代表着芽目前的冷激进度。当Sc达到阈值C时的日期t2即为休眠期被打破的日期（式（3））。参数k，l确定了静止期发育速度对日平均气温的响应函数Rf（xt）（也称驱动单元，forcing units）。Sf是驱动单元的累积和，代表当前的驱动进度。当Sf达到阈值G时的日期td就是始花期或盛花期（式（4））。

2.1.3 统计模型

统计模型主要是利用物候事件发生的时间与气候因子的相关性建立物候与气象因子之间的对应关系。这种模型较少考虑植物的生理生态过程，只进行物候期与每年不同时期气温的简单回归分析［17-18］。本文使用以下一元线性回归方程模拟春季物候期：

其中，y是预测的植物物候期（日序），Tm是m月份的平均气温，h是回归系数，z是截距。本文首先计算物候期与前5个月气温的相关系数，找出最相关的m月份。通过计算，发现3种观赏植物的花期与3月平均气温最相关，故建立了3种观赏植物花期与3月平均气温的统计模型。

2.2 物候模型参数估计

使用物候期序列中所有年的观测数据进行模型参数值估计。3种模型的参数值估计均采用最小二乘法原则［5］，

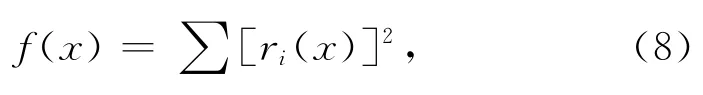
其中，x代表参数空间，ri（x）＝di（x）－diobs，di（x）和diobs分别代表第i个样本用参数空间x确定的模型预测日期和观测日期。使f（x）最小的模型参数组合即为最优的参数组合。对于统计模型，可直接导出最小二乘解析解。而对于SW模型和UniChill模型，该问题变成了一个非线性最小二乘问题，无法推导出解析解，所以本文选取模拟退火算法实现最优参数的估计［5］。

2.3 物候模型检验

求出最优模型参数后，利用气象观测资料模拟出逐年的花期。为了检验模型的准确性，采用内部检验和交叉检验结合的方式进行［13，18］。先进行内部检验，即用全部观测年份拟合出的参数模拟出物候序列；再将观测序列与模拟序列进行对比，计算方差解释量（ES）和均方根误差（ERMS）［13］。其次进行交叉检验（又称外部检验［13］）。交叉检验采用逐个剔除法，即将某年份的观测值剔除后，利用其他年份的数据拟合参数，模拟出被剔除年的物候期。将每一年份的观测值逐一剔除一次后，即可得到用于交叉检验的序列。同样将此序列与物候观测序列作对比，计算ES和ERMS，交叉检验可以检验模型在独立的情况下能否准确地模拟物候期。

3 结果分析

3.1 模型拟合及检验结果

由模拟效果图（图2～图4）可以看出，SW模型对白玉兰始花期模拟稍差（观测值与模拟值散点图偏离y＝x的基准线较多），但在杭州早樱始花期和盛花期、白玉兰盛花期、山桃始花期和盛花期模拟中，SW模型的模拟值与观测值散点图均接近于y＝x的基准线，表现出比UniChill模型和统计模型更优的模拟效果。另外，从年际变化曲线看，SW模型模拟的花期序列和实际观测序列也更为吻合（图5）。这说明，SW模型比其他两种模型相比能更好地预测观赏植物开花期。

表2为模拟不同观赏植物花期的SW模型参数。结果表明，3种植物开花的界限温度为0～3℃。研究［27］指出，一般植物在0～35℃的温度范围内，随温度上升生长迅速。因此，本文得到的界限温度在此范围内。基于上述界限温度，3种植物开花所需积温G各不相同，介于124～181℃·d之间。检验结果表明，SW模型内部检验的ES为0.84～0.94（达到0.001的显著性水平），ERMS为1.60～3.05 d（表2）。UniChill模型具有较多的参数，因此其内部检验准确度极为突出，ES为0.85～0.93（达到0.001的显著性水平）；ERMS为 1.69～2.74 d （表3）；从统计模型的表现来看，内部检验的ES为0.67～0.86（达到0.001的显著性水平），ERMS为2.15～3.62 d（表4）。

图2 SW模型、UniChill模型和统计模型模拟的杭州早樱始花期和盛花期Fig.2 Effectiveness of SW Model，UniChill Model and Statistical Model for simulating the flowering date and the full flowering date ofPrunus discoidea

表2 SW模型模拟3种植物始花期和盛花期的模型参数及其检验结果Table 2 Model parameters and test results of SW Model for simulating the first flowering date and the full flowering date of three plants

然而，内部检验并不能表示物候模型的模拟效果，模型的适用性要通过外部检验结果来评估。从交叉检验的结果来看，SW 模型的ES为0.74～0.91（达到0.001的显著性水平），ERMS为1.93～3.58 d；UniChill模型的ES为0.68～0.88，ERMS为2.49～3.79 d；统计模型的ES为0.56～0.83，ERMS为2.36～4.24 d。将3种模型交叉检验的ES和ERMS列于表5，进行效果比对。结果表明，SW模型适用性最高，UniChill模型次之，统计模型最差。

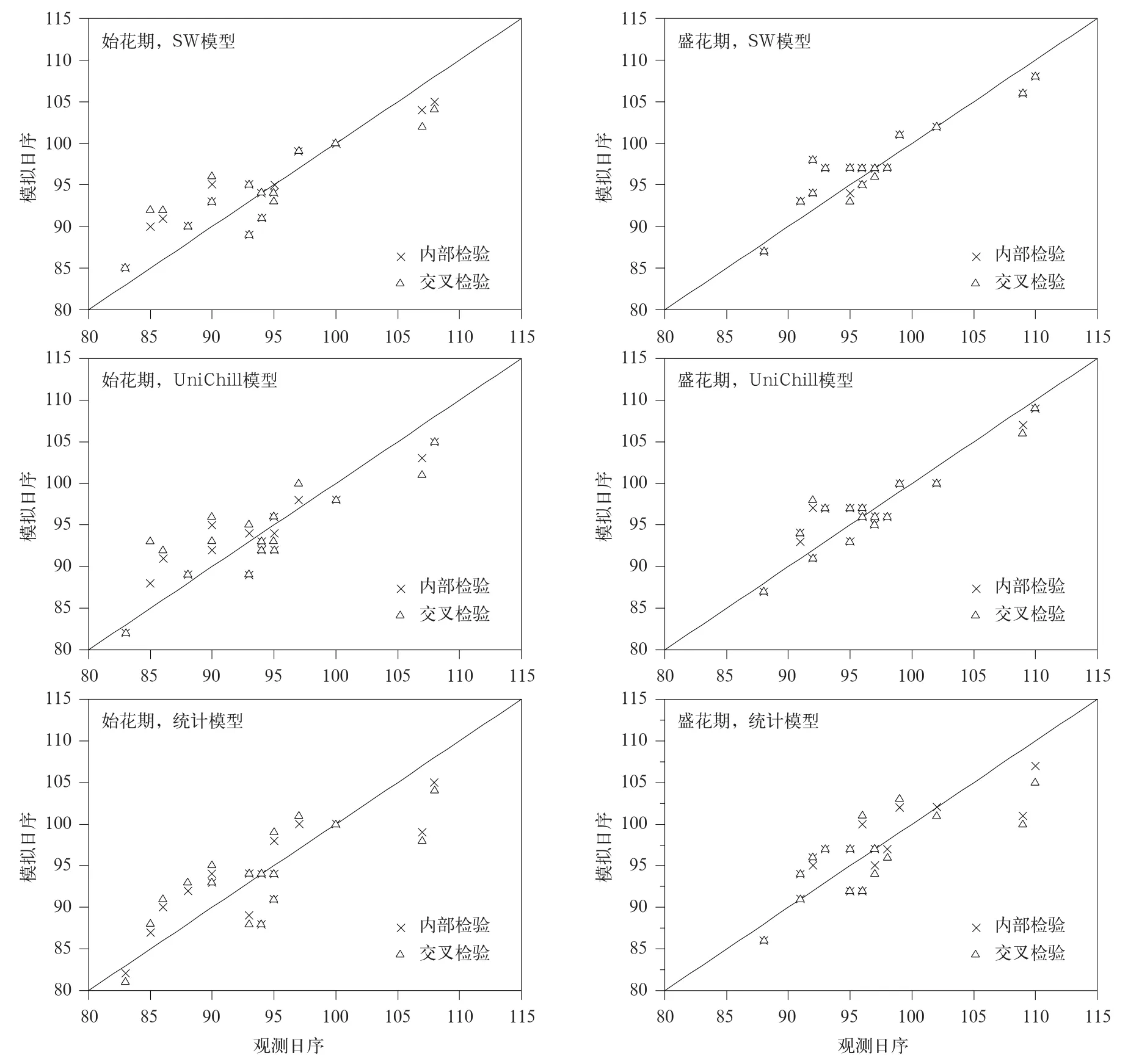
图3 SW模型、UniChill模型和统计模型模拟的白玉兰始花期和盛花期Fig.3 Effectiveness of SW Model，UniChill Model and Statistical Model for simulating the flowering date and the full flowering date ofMagnolia denudata

表3 UniChill模型模拟3种植物始花期和盛花期的模型参数及其检验结果Table 3 Model parameters and test results of UniChill Model for simulating the first flowering date and the full flowering date of three plants

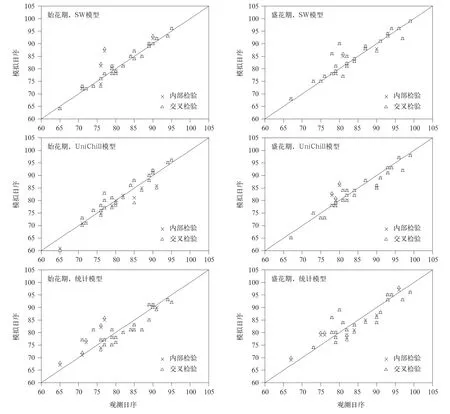
图4 SW模型、UniChill模型和统计模型模拟的山桃始花期和盛花期Fig.4 Effectiveness of SW Model，UniChill Model and Statistical Model for simulating the first flowering date and the full flowering date ofAmygdalus davidiana

表4 统计模型模拟3种植物始花期和盛花期的模型参数及其检验结果Table 4 Model parameters and test results of Statistic Model for simulating the first flowering date and the full flowering date of three plants

图5 1982—2012年观测与模拟的山桃始花期和盛花期序列Fig.5 The observed and simulated the first flowering date and the full flowering date ofAmygdalus davidianafrom 1982 to 2012

表5 SW模型、UniChill模型和统计模型的交叉检验结果对比Table 5 Cross-validation results of SW Model，UniChill Model and Statistic Model

3.2 开花期预测准确率

为了直观对比3种模型在北京地区观赏植物开花期预测中的适用性，将实际观测序列与逐一剔除法得到的模拟序列作对比，如果两者之差绝对值小于3 d（定义误差在3 d之内为准确），则认为预测正确，记录为“1”，否则认为预测错误，记录为“0”。然后统计“1”的数量占相应序列总年数的百分比，即为预测准确率。结果表明（表6），SW模型在模拟杭州早樱始花期和盛花期、白玉兰盛花期、山桃始花期和盛花期方面，其预测准确率均最高，只在白玉兰始花期模拟方面，预测准确率低于UniChill模型，但仍然高于统计模型。该结果进一步证明SW模型在北京地区3种植物开花期预测中的适用性最高。

表6 SW模型、UniChill模型和统计模型预测观赏植物开花期准确率（单位：%）Table 6 Predicting accuracy of SW Model，UniChill Model and Statistical Model for simulating the flowering date of three plants（unit：%）

4 结论与讨论

本文以北京地区玉渊潭公园杭州早樱、密云农业气象试验站白玉兰、颐和园公园山桃多年物候观测资料和海淀气象站、密云气象站1981—2012年逐日平均气温观测资料序列为基础，分别对3种物候模型（SW模型、UniChill模型和统计模型）在北京地区观赏植物开花期预测方面的适用性进行分析，得到以下结论：

1）SW模型交叉检验的方差解释量最高（0.74～0.91），均方根误差最小（1.93～3.58 d），其次为UniChill模型，统计模型具有最低的方差解释量和最大的均方根误差。因此，SW模型在模拟观赏植物花期方面有最低的误差。

2）在预测准确率方面，SW模型模拟结果的误差在3 d之内的年份占总年份的85%以上（白玉兰始花期除外），同样在3种模型中表现最好。因此，SW模型在北京地区3种植物开花期预测中适用性最高。

最为复杂的UniChill模型在模拟独立数据方面弱于更为简单的SW模型，其主要原因可能是这3个物种均主要分布于我国北方温带地区，冬季冷激需求一般均能满足，因此决定性因素还是春季温暖积温。SW模型只针对这一积温时段模拟，因此模拟效果更好。

本研究中统计模型是简单的数理统计方法，且只考虑了植物开花期与前期月平均温度的关系，未使用日或候平均温度作为自变量，也未考虑温度以外其他气象要素（如光照和水分等）的影响，因此模拟效果最差，统计模型仍有很大的提升和改进空间。徐琳等［28］指出刺槐开花日期还可能受到其他气象因子如光周期、降水量等的影响，韩小梅等［29］同样指出植物物候还在较大程度上受到水分和光照等气象因素的影响，因此，如果统计模型在日平均气温的基础上，再考虑光照和水分的综合影响以及植物生理过程［30］，或将获得更好的效果。此外，在气候变化［31-32］和北京市热岛效应不断增强［33-38］的情况下，采用SW模型对城乡不同地点和未来不同时期植物花期的预测上可能存在适用性问题，需要根据新的观测资料改进模型或订正预测结果。

［1］ 李荣平，周广胜，阎巧玲.植物物候模型研究.中国农业气象，2005，26（4）：210-214.

［2］ 裴顺祥，郭泉水，辛学兵，等.国外植物物候对气候变化响应的研究进展.世界林业研究，2009，22（6）：31-37.

［3］ Sarvas R.Investigation on the annual cycle of development of forest trees：Autumn dormancy and winter dormancy.Commun Inst For Fenn，1974，84：10.

［4］ Cannell M G R，Smith R I.Thermal time，chill days and prediction of budburst in Picea sitchensis.J Appl Ecol，1983，20（1）：951-963.

［5］ Chuine I，Cour P，Rousseau D D.Fitting models predicting dates of flowering of temperate-zone trees using simulated annealing.Plant，Cell&Environment，1998，21（5）：455-466.

［6］ Chuin Cour P，Rousseau D D.Selecting models to predict the timing of flowering of temperature trees implications for tree phenology modellintg.Plant，Cell&Environment，1999，22（1）：1-13.

［7］ Chuine I.A unified model for budburst of trees.Journal of Theoretical Biology，2000，207（3）：337-347.

［8］ Hunter A F，Lechowicz M J.Predicting the timing of budburst in temperate trees.J Appl Ecol，1992，29（3）：597-604.

［9］ Landsberg J J.Apple fruit bud development and growth：A-nalysis and empirical model.Ann Bot，1974，38：1013-1023.

［10］ Murray M B，Cannell M G R，Smith R I.Date of budburst of fifteen treespecies in Britain following climatic warming.J Appl Ecol，1989，26：693-700.

［11］ Cannell M G，Smith R I.Thermaltime，chilling days and prediction of budburst in Picea sitchensis.J Appl Ecol，1983，20（3）：951-963.

［12］ Hunter A F，Lechowicz M J.Predicting the timing of budburst in temperate trees.J Appl Ecol，1992，2：597-604.

［13］ 王焕炯，戴君虎，葛全胜.1952—2007年中国白蜡树春季物候时空变化分析.中国科学：地球科学，2012，42（5）：701-710.

［14］ Chuine I，Yiou P，Viovy N，et al.Historical phenology：Grape ripening as a past climate indicator.Nature，2004，432：289.

［15］ 宋富强，张一平.动态物候模型发展及其在全球变化研究中的应用，生态学杂志，2007，26（1）：115-120.

［16］ Morin X，Viner D，Chuine I.Tree species range shifts at a continental scale：New predictive insights from a process-based model.J Ecol，2008，96：784-794.

［17］ Spieksma F T M，Emberlin J C，Hjelmroos M，et al.Atmospheric birch（Betula）pollen in Europe：Trends and fluctuations in annual quantities and the starting dates of the seasons.Grana，1995，34（1）：51-57.

［18］ 戴君虎，王焕炯，葛全胜.近50年中国温带季风区植物花期霜冻风险变化.地理学报，2013，68（5）：593-601.

［19］ 李荣平，周广胜，王笑影，等.不同物候模型对东北地区作物发育期模拟对比分析.气象与环境学报，2012，28（3）：25-30.

［20］ 张谷丰，孙雪梅，张志春，等.物候模型预测稻纵卷叶螟发生期的应用研究.福建农业学报，2013，28（2）：148-153.

［21］ 张福春.北京春季的树木物候与气象因子的统计学分析.地理研究，1983，2（2）：55-64.

［22］ 郝日明，张璐，张明娟，等.影响南京桂花秋季开花期变化的关键气候因子研究.植物资源与环境学报，2006，15（3）：31-34.

［23］ 刘流，甘一忠.桃花迟早年型的冬季气候特点及花期预测.气象，2006，32（1）：113-116.

［24］ 韩亚东，于长文，刘雪峰.京桃春季物候期与气温之间的关系.安徽农业科学，2007，35（15）：4517-4518.

［25］ 陈正洪，肖玫，陈璇.樱花花期变化特征及其与冬季气温变化的关系.生态学报，2008，28（11）：5209-5217.

［26］ 张菲，邢小霞，李仁杰.利用地温构建菏泽牡丹花期预测模型.中国农业气象，2008，29（1）：87-89.

［27］ 祝廷成，钟章成，李建东.植物生态学.北京：高等教育出版社，1988.

［28］ 徐琳，陈效逑，杜星.中国东部暖温带刺槐花期空间格局的模拟与预测.生态学报，2013，33（12）：3584-3593.

［29］ 韩小梅，申双和.物候模型研究进展.生态学杂志，2008，27（1）：89-95.

［30］ 谭美，王四清.观赏植物生长模拟模型研究进展.园艺学报，2010，37（9）：1523-1530.

［31］ 赵平，南素兰.气候和气候变化领域的研究进展.应用气象学报，2006，17（6）：725-735.

［32］ 任玉玉，任国玉，周江兴.我国大陆大尺度气候观测网的理想密度和分布.应用气象学报，2012，23（2）：205-213.

［33］ 曲绍厚，宋锡铭，李玉英.北京城区的气象效应.地球物理学报，1981，24（2）：229-237.

［34］ 郑祚芳，刘伟东，王迎春.北京地区城市热岛时空分布特征.南京气象学院学报，2006，29（5）：694-699.

［35］ 张光智，徐祥德，王继志，等.北京及周边地区城市尺度热岛特征及其演变.应用气象学报，2002，13（特刊）：43-50.

［36］ 杨玉华，徐祥德，翁永辉.北京城市边界层热岛的日变化周期模拟.应用气象学报，2003，14（1）：61-68.

［37］ 郑祚芳，范水勇，王迎春.城市热岛效应对北京夏季高温的影响.应用气象学报，2006，17（增刊Ⅰ）：48-53.

［38］ 石英，高学杰，吴佳.华北地区未来气候变化的高分辨率数值模拟.应用气象学报，2010，21（5）：580-589.

Applicability Analysis of Phenological Models in the Flowering Time Prediction of Ornamental Plants in Beijing Area

Zhang Aiying1）Wang Huanjiong2）3）Dai Junhu2）Ding Deping1）

1）（Beijing Meteorological Service Center，Beijing100089）
2）（Institute of Geographic Science and Natural Resources，CAS，Beijing100101）
3）（University of Chinese Academy of Sciences，CAS，Beijing100049）

In recent years，with the tourism booming and the increasing demands for flower-appreciation，the prediction of flowering date of ornamentals plants becomes more and more important.For a long time，phenological models are widely used in agriculture field，but rarely applied in predicting flowering time of ornamental plants.

Based on phenological data of three ornamentals plants（Prunus discoidea，Magnolia denudataandAmygdalus davidiana）in Beijing Area，corresponding meteorological data during the period of 1981－2012 at Haidian and Miyun meteorological stations，three phenological models（SW Model，UniChill Model and Statistical Model）for simulating the first flowering date and the full flowering date of the above three plants are developed.In the experimental process，the least square fitting is introduced in computing parameters，including linear least square fitting in Statistical Model and nonlinear least square fitting in SW Model and UniChill Model.Moreover，the simulating annealing approach is used to obtain the analytic solutions for SW Model and UniChill Model.Results show that SW Model performs well in simulating the first flowering date and the full flowering date ofPrunus discoidea，the full flowering date ofMagnolia denudata，and the first flowering date and the full flowering date ofAmygdalus davidiana.Besides，SW Model is the most applicable model with the root mean square error（RMSE）of external verification between 1.93－3.58 days.UniChill Model ranks the second with the RMSE of 2.49－3.89 days，and Statistical Model has the largest uncertainty with the RMSE of 2.37－4.24 days.As far as prediction accuracy is concerned，SW Model also ranks the first，and for more than 85%of years，the prediction error is within 3 days.

Above all，SW Model is recommended for predicting the flowering dates of the ornamental plants inBeijing Area.But Statistical Model based on daily average temperature，considering the comprehensive effect of light and moisture and plant physiological processes，may perform better.With the increasing urban heat island effect in Beijing Area，the deviation caused by urban heat island effect should be removed during the application of SW Model.

phenological models；flowers blooming；prediction；applicability

张爱英，王焕炯，戴君虎，等.物候模型在北京观赏植物开花期预测中的适用性.应用气象学报，2014，25（4）：483-492.

2014-01-11收到，2014-05-05收到再改稿。

北京市自然科学基金项目（8112028），国家自然科学基金项目（41030101）

*email：bjzhangay＠bjmb.gov.cn