带中心锥航空发动机腔体电磁散射特性数值研究

杨胜男，张志学，邵万仁，邓洪伟

（中航工业沈阳发动机设计研究所，沈阳110015）

带中心锥航空发动机腔体电磁散射特性数值研究

杨胜男，张志学，邵万仁，邓洪伟

（中航工业沈阳发动机设计研究所，沈阳110015）

为了研究中心锥顶角和电磁波入射方位改变对航空发动机腔体的电磁散射特性的影响，采用物理光学（PO）法和等效棱边电磁流（EEC）法,对带中心锥发动机腔体在C波段入射频率f=6 GHz下进行电磁散射计算。计算结果表明：在水平极化下入射角为4°～28°范围内，中心锥顶角30°的发动机腔体的雷达散射截面（RCS）值较小；由等效电流图上得到特定角度下发动机腔体散射强弱分布，为发动机腔体关键散射区域采取隐身措施以提高隐身性能提供参考。

中心锥；发动机腔体；雷达散射截面；物理光学法；等效棱边电磁流法；隐身

0 引言

良好的隐身性能是提高飞机攻击力和生存率的重要手段，成为先进飞机及其发动机的重要技术特征和主要技术指标。隐身主要包括雷达隐身和红外隐身。其中雷达根据目标发出电磁波的能量来判断其形状，并确定其位置和运动状态，因此实现发动机雷达隐身的直接手段就是控制和降低发动机自身的雷达散射截面（RCS）。

发动机腔体结构由前向腔体结构（包括进气道和风扇等）和后向腔体结构（包括低压涡轮、加力燃烧室、喷管等）2部分组成，是飞机的主要散射源之一。中心锥作为发动机腔体的典型结构（如风扇帽罩锥体和加力燃烧室中心锥），对飞机前、后向雷达散射贡献较大，这种结构的散射来自与腔体壁面之间多次反射和绕射等相互作用，是1种强回波散射[1]，影响其电磁散射特性的因素很多。

本文以航空发动机腔体RCS减缩为目标，进行带中心锥的发动机腔体模型的数值模拟计算，分析中心锥顶角和电磁波入射方位改变对发动机腔体RCS的影响。

1 RCS基本概念

电磁波在空间传播过程中遇到障碍物会发生散射，雷达利用这种特点来发现并测定未知目标。RCS是目标的1种假想面积，用来定量表征目标散射强弱。

RCS定义为

式中：R为目标与天线之间的距离；Ei、Hi分别为雷达波入射到目标所在位置上的电场强度和磁场强度；Es、Hs分别为目标散射场在雷达天线处，可被天线接收的电场强度和磁场强度。

σ的单位为m2。为便于运算和分布曲线的表达，在多数情况下，σ的单位取作dBm2（分贝平方米）。用以上2种单位表示的RCS存在如下换算关系

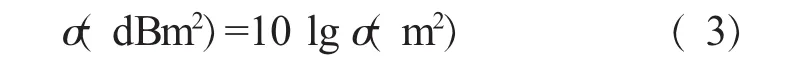
2 电磁计算方法

式中：R为目标到雷达天线的距离；Ss为天线位置上目标散射的功率密度；Si为目标所在位置天线辐射功率密度。

引入电场和磁场的概念，式（1）还可表述为

根据波长和散射体特征尺寸的大小，散射过程分为低频区、谐振区和高频区。目前对军用飞机构成威胁的雷达探测波段主要为厘米波段。相对于波长，发动机腔体属于电大尺寸腔体结构，其散射过程属于高频区，相应的雷达散射计算应采用高频电磁计算方法。目前常用的高频算法主要有几何光学法、几何绕射理论、物理光学法、物理绕射理论、等效电磁流法、积分方程法和时域方法等[2-5]。根据发动机腔体的电磁散射计算特点，本文选择物理光学法和等效电磁流法相结合的算法。

2.1 物理光学(PO)法

PO理论[2,6-7]是用散射体表面的感应电流取代散射体，通过对表面感应场的近似和积分求得散射场。F.Obelleiro等人提出的物理光学迭代法[8]，将迭代方法应用于分析腔体散射特性，近似模拟电磁波在腔体结构各部分间的多次反射等相互作用过程。与其他高频算法相比，该方法迭代过程简单，不需要矩阵求逆，适合电大尺寸腔体散射特性的分析计算。

由理想导电壁构成的开口腔体如图1所示。入射波由开口Sa进入后，将在腔体内部Sc产生散射场，最终回波从入口处退出。若忽略边缘和外部散射的贡献，其散射场来自电磁波在腔体内部的多次反射。

图1 腔体结构

设入射均匀平面波（E（ra），H（ra））照射在 Sa面上，在腔体内部Sc面上产生等效电磁流（E（rc），H（rc））由Kirchhoff公式得到

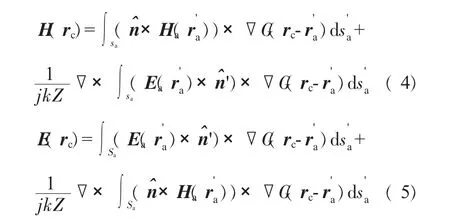
腔壁Sc上的等效感应电流密度由磁场积分方程(MFIE)[9-10]迭代得到

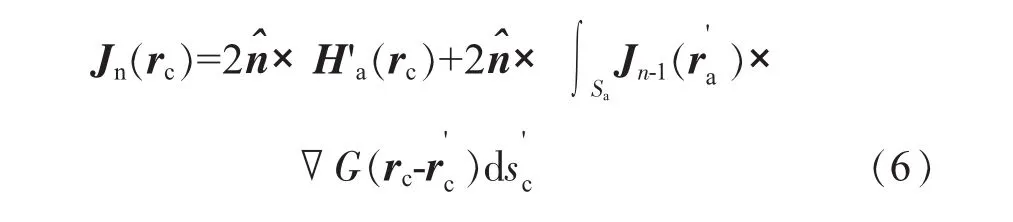
2.2 物理光学法的改进

对于轴向尺寸大于直径尺寸的管状腔体结构，入射电磁波在腔体壁面间多次反射，大大降低了迭代数值方法的计算效率。为此引入前、后向迭代技术[11-12]和松弛因子应用于物理光学法的计算，加快迭代的收敛性。

应用前、后向迭代算法，计算腔体内壁真实电流密度，并加入松弛因子ω（0＜ω≤1）加速收敛前向迭代（i=1,2,…，N）

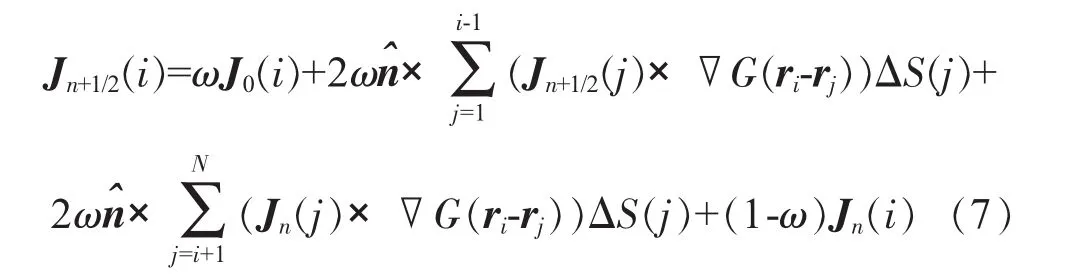
后向迭代

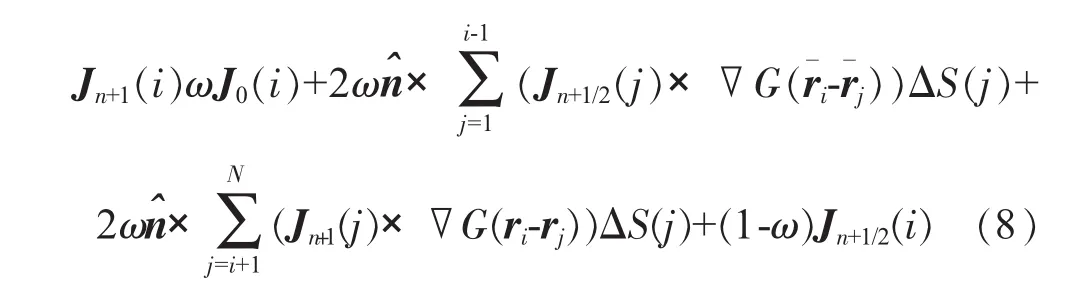
式中：n为迭代次数；ω为收敛因子（0＜ω≤1）。

2.3 等效电磁流（EEC）法

PO方法在处理腔体边缘散射时存在缺陷，因此引入等效电磁流法来处理腔体边缘的绕射问题。EEC法直接组合等效电磁流移去射线方法解的奇异性，是求解边缘绕射场应用最广泛的方法。常用形式有Mitzner的增量长度绕射系数[13]和Michaeli的等效电流[14]。本文应用Michaeli的表述，对于边缘为C的任意尖劈，其远区边缘绕射场表示为式中：sˆ为观察方向单位矢量；tˆ为C的切向单位矢量；r'为从原点到边缘上某点的径向矢量；dl为沿C的弧长增量。

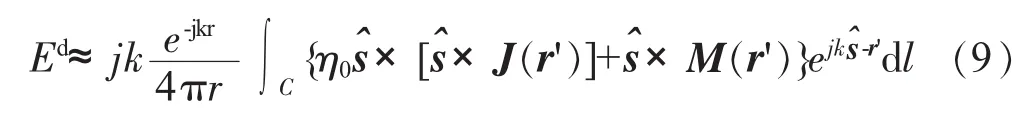
式（9）中各参数关系如图2所示(虚线分别为入射和观察方向在xy平面上的投影)。

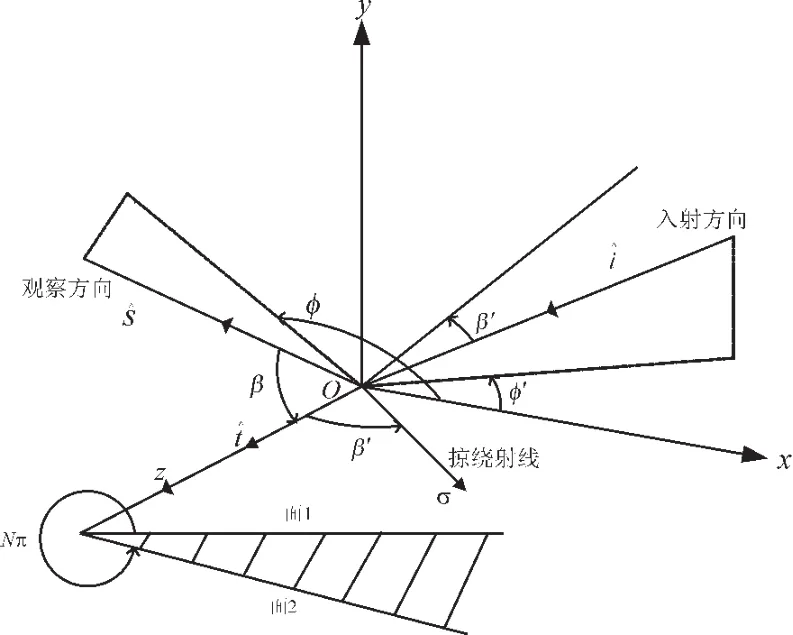
图2 尖劈散射结构

等效边缘线电流J（r'）和线磁流M（r'）可以进一步表达为

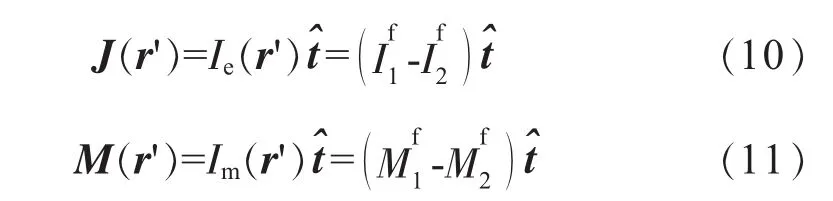
用等效电磁流减去物理光学的贡献，得到边缘散射贡献的结果

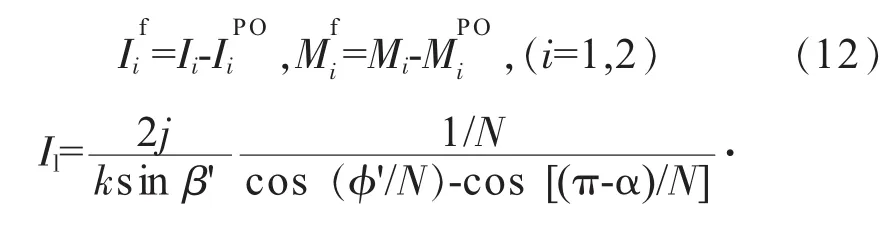
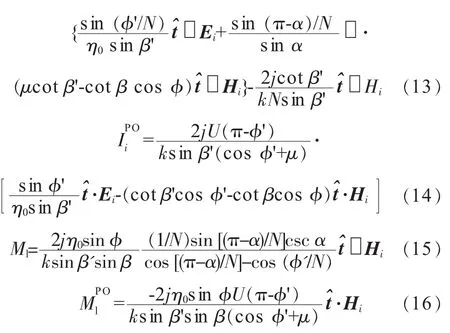
式中：Nπ为外劈角；U（x）为单位阶跃函数；α=arccos为了得到和，需作以下代换：

3 程序验证

为验证程序的计算精度，对金属平板进行RCS计算，将计算程序得到的数值解与理论解进行对比。

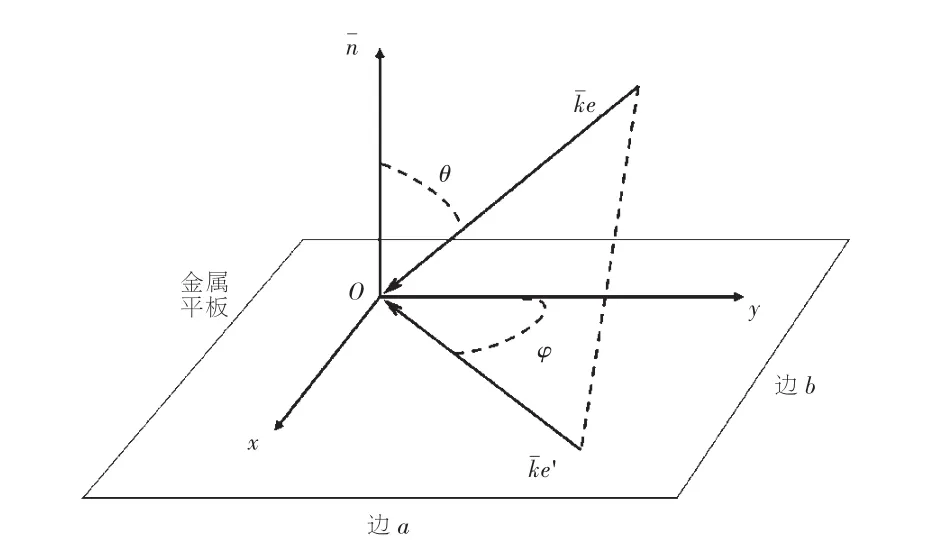
图3 平板计算模型

计算模型设置如图3所示，图中⇀n是平面法向量。有限尺寸的金属平板高频区理论解为

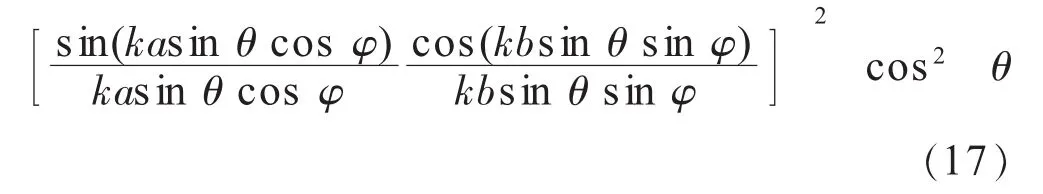
式中：A为金属平板的面积，其值等于边长a与b的乘积；λ为入射波波长。

取a=b=16.5 cm、λ＝5 cm，水平极化方式下进行计算，程序的数值解与理论解比较如图4所示。

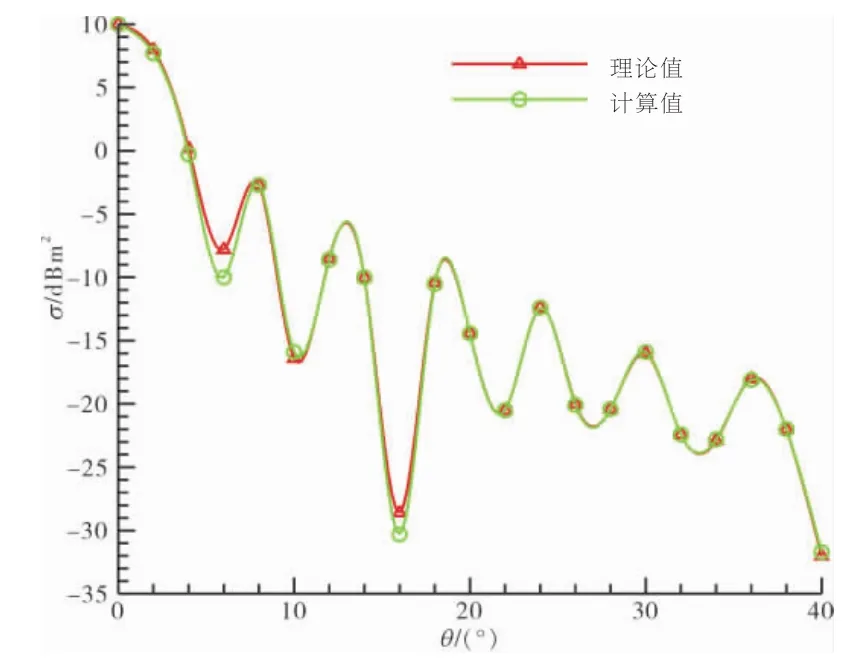
图4 水平极化平板RCS理论值与计算值

比较计算结果，程序计算值与理论精确解的RCS曲线整体趋势一致，结果基本吻合，平均误差为2.1%，程序计算精度较好，结果可信。

4 带中心锥的发动机腔体RCS计算与分析

4.1 计算模型与状态

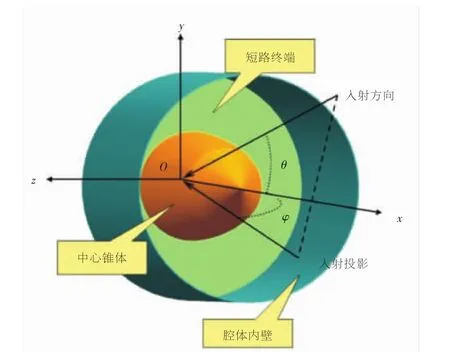
图6 加力腔体简化模型

图7 中心锥体角度修形方案

本文以发动机后腔体 （具体结构如图5所示）为例进行建模。发动机后腔体前端为低压涡轮叶片，相关研究显示短路终端与叶片终端的电磁散射结果误差在可以接受的范围内[15]。中心锥后端为一定数量的火焰稳定器和喷油杆等，其轴向投影面积远小于中心锥结构。故本文将发动机后腔体做简化处理，并忽略稳定器和喷油杆等结构的影响，仅针对中心锥顶角进行修形研究。简化的计算模型如图6所示。柱体高1190 mm，直径为470 mm，中心锥体依据等压力梯度设计，由前部锥体收敛段和顶端尖锥2部分组成，保持收敛段长度500 mm不变，使中心锥半顶角α（即锥尖与x轴之间的角度）分别为30°、50°、70°和85°（如图7所示），基础模型basic为无中心锥空腔体。

目前对军用飞机构成威胁的雷达波段主要有Ku、X、C、S和L波段，均属于厘米波段。综合考虑计算精度和计算效率选取C波段，入射频率f=6 GHz，即波长λ=5 cm。根据腔体开口位置，设定雷达发射的平面电磁波由yOz平面右侧(即x轴正方向)射入。其中，入射波电场矢量与xOz平面夹角标记为θ，与xOy平面夹角标记为φ。取φ=0°，θ=-44°荠44°，取值间隔为2°。本文对单站雷达系统进行模拟，得到计算水平极化和垂直极化方式下5种模型的RCS随中心锥顶角α变化的曲线。

4.2 计算结果分析

4.2.1 RCS分布曲线特征分析

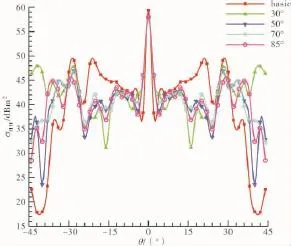
图8 水平极化RCS总场分布

水平极化、垂直极化RCS总场分布分别如图8、9所示，水平极化和垂直极化下边缘绕射RCS分布如图10所示。从图8～10中可见，在2种极化方式下，计算模型RCS分布曲线均以θ=0°为中心对称分布，这是由所选定模型的结构形式决定的；5种模型均以x轴为中心轴360°对称，当入射角度θ=0°时，入射波传播方向与x轴垂直，因此RCS曲线以左右对称的形式呈现。观察如图10所示的边缘散射情况，由于各模型腔体开口结构相同，在相同极化方式下边缘散射情况也完全相同，且水平极化方式下的散射强度大于垂直极化入射的情况。

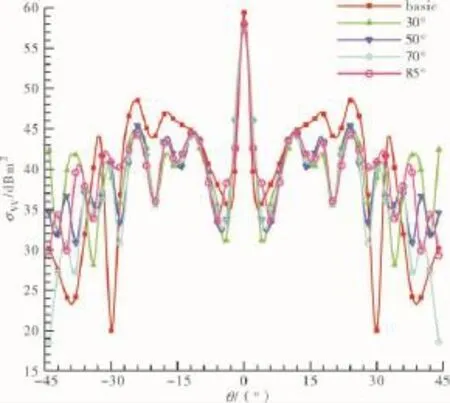
图9 垂直极化RCS总场分布

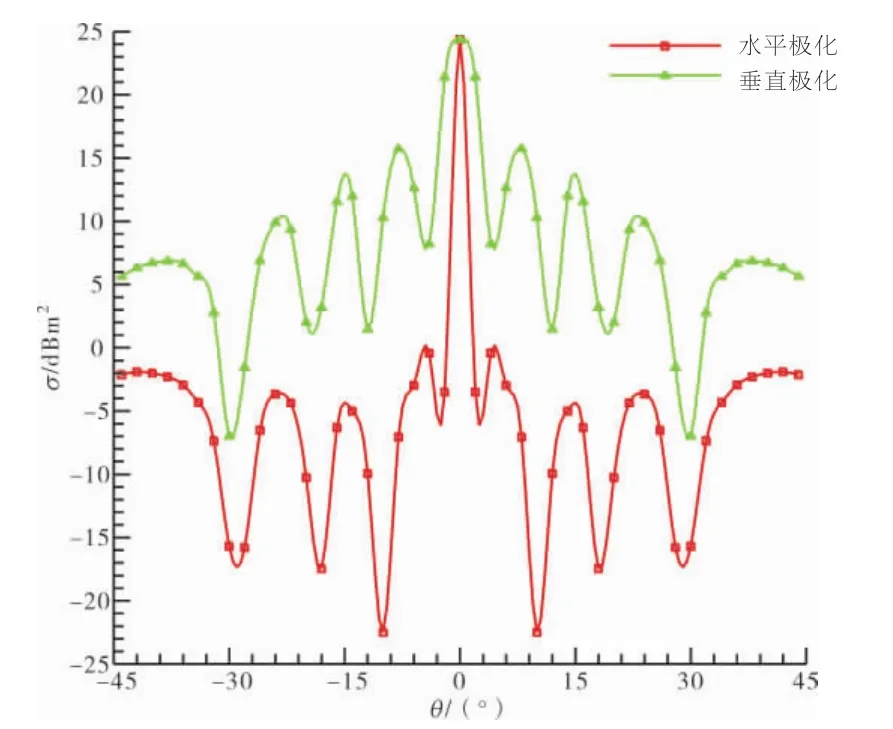
图10 水平极化和垂直极化下边缘绕射RCS分布

模型RCS总场分布曲线呈现出区域性特点，具体的RCS平均数值σ见表1、2。各模型的RCS分布曲线在θ=0°处达到峰值，且数值大小与极化方式无关。在θ=0°时，各模型中基础模型的平均值σ最大，达到59.41 dBm2；α=85°的模型次之，达到58 dBm2，其余3个模型的基本相同，约为57.4 dBm2。此峰值由法向镜面回波和边缘绕射回波共同形成，从边缘散射场的情况来看，在θ=0°时入射电磁波矢量与腔体边缘正好平行(或垂直)，此时回波最为强烈[16]。从腔体内部散射场情况来看，在θ=0°时，暴露在入射电磁场下腔体截面积最大，其腔体内部结构参与电磁波的散射,而不存在所谓入射波无法达到的“暗区”，形成强烈的后向散射回波从腔体出口反射出去，被接收雷达捕捉。

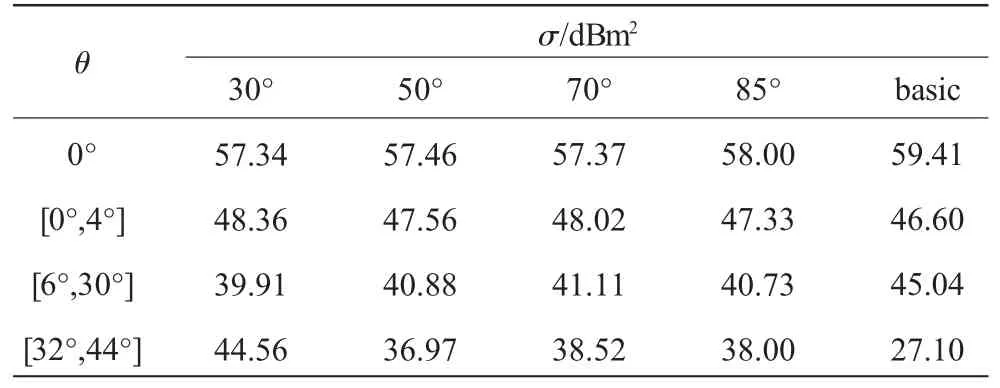
表1 水平极化下不同角度区间内各模型RCS平均值

表2 垂直极化下角度区间内RCS平均值

RCS总场分布曲线在θ=0°时达到峰值后，随后在θ=2°荠4°的入射角度处，达到1个明显低点（图8、9），这是由于随着入射角度的偏移，部分电磁波的传递路线被壁面遮挡，相比较在θ=0°入射时完全无遮挡的情况，σ迅速减小。随着入射角度继续偏离中心轴，电磁波在腔体内与壁面间形成多次反射，RCS略有增大并保持在一定范围内震荡分布。在小角度情形下（水平极化下θ∈[0°，4°]，垂直极化下θ∈[0°，2°]），法向镜面的首次回波对后向散射起主要作用。从表1、2中可见，带中心锥的腔体模型RCS平均值σ略高于基础模型的；4种带中心锥的腔体模型的水平极化RCS平均值σ最大约相差1 dBm2，垂直极化RCS平均值σ最大相差约1.5 dBm2。

水平极化方式下入射角度在6°～30°范围内，4种带中心锥的腔体模型的RCS平均值σ相差最大约1.2 dBm2，带中心锥的腔体模型的散射明显低于基础模型的（表1），体现出尖锥体在接受头向入射波时对RCS的衰减作用。其中锥顶角度为30°的腔体模型的RCS平均值σ达到39.91 dBm2，比基础模型RCS平均值减缩11.4%。其他3种中心锥腔体模型RCS平均值σ之间相差值不大于2.3%，比基础模型RCS平均值减缩量不大于9.5%。当入射角度大于30°时所呈现的趋势与之前相反，基础模型表现出较低的RCS平均值，锥顶角度为30°的腔体模型RCS平均值最大。这是因为在不使用雷达吸波材料的情况下，由入射场与散射场构成的RCS空间总场是一定的，修形技术是将散射回波从1个接收角度转移到另1个角度，或者将后向散射变为非后向散射，往往在某些角度内获得RCS减缩，同时伴随这另一些角度RCS的增大[7]。这也可以解释在垂直极化方式下（具体数据见表2），带中心锥的腔体模型在θ=4° ～28°内对RCS的减缩作用没有水平极化下的大 (比基础模型RCS平均值σ最大减缩8.8%)，但其在θ=32°～44°内RCS平均值的反弹也不大。

4.2.2 感应电流云图特征分析

当电磁波照射物体时，入射波在散射体上产生感应电流，RCS所度量的散射场就是由感应电流的辐射效应引起的。采用PO理论求解目标散射场的过程中，利用散射体表面感应电流取代散射体，因此计算模型的表面感应电流大小一定程度上可以反映其RCS大小。本文选取中心锥顶角为30°的腔体模型和基础模型在具有代表性的3个入射角度下的表面感应电流云图 （分别如图11、12所示），来分析这2种模型RCS的变化特点。

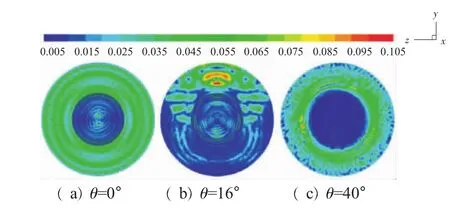
图11 水平极化下锥顶角为30°的模型3种入射角度感应电流分布

图12 水平极化下基础模型3种入射角度感应电流分布

从图11、12中可见，从左到右分别显示模型在水平极化方式下入射角度为0°、16°和40°时的感应电流大小，其趋势与第4.2.1节中RCS计算和分析结果一致。当θ=0°时，腔体底部感应电流对RCS的贡献突出，这与电磁波的镜面反射回波有关，其整个电流场强度也大于其他2种情况。此时中心锥结构对腔底部的散射起到了一定的占位作用[16]，但却在底部其他区域造成了散射作用的增强。当电磁波以θ=16°入射时，腔体下方壁面对其内部起到了遮挡作用，同时由于壁面与中心锥之间耦合散射在腔体上方形成1个高强度区，图中显示此区域感应电流强度明显低于其上方区域的，可以观察到此时中心锥结构明显降低了中心区域的感应电流强度。θ增大到40°时，入射波不能直接到达中心锥表面，到达腔体内壁面的电磁波在腔体内部不断散射，最终从入口退出。虽然中心锥自身感应电流较小，但这是以周围区域感应电流增大为代价的，这个角度下基础模型RCS平均值较小。

5 结论

（1）电磁波以θ=0°入射时，法向镜面回波和边缘绕射回波共同形成RCS峰值，各模型σ值相差小于2 dBm2；θ=2°、4°时，各模型RCS曲线分别达到第1个波谷；在水平极化下θ∈[6°，30°]（垂直极化下θ∈[4°，28°]）范围内，基础模型RCS值σ明显高于其他带中心锥的腔体结构的，中心锥结构形式对腔体散射减缩优势在小角度下体现明显；在θ＞30°区域RCS分布曲线与前一角度区域呈现相反趋势。

（2）中心锥顶角为30°的腔体模型在θ∈[6°，30°]内水平极化方式下σ最小，较无锥腔体减小11.4%，为该型发动机腔体减小RCS设计提供了参考。发动机类腔体散射机理复杂，需要进行多角度优化分析才能找到最佳的小RCS结构形式。

（3）RCS总场由腔体内部散射和边缘绕射2部分组成，可以通过采用适当的出口边缘修形等方式减小腔体入口边缘散射，以此来达到RCS减小的目的。

（4）随着入射角度θ的变化，发动机腔体各区域内RCS分布呈现不同趋势，说明单纯采用修形方式往往在某些角度获得RCS减小，但不可避免造成另一些区域RCS的增大。如果要求所有方向上都能获得RCS减小效果，需要采取修形技术与雷达吸波材料相结合的方式。

（5）由腔体表面的感应电磁流分布图可以得到入射电磁波激起感应电流的重点部位，可为在类似腔体内关键散射区域涂覆吸波涂层或采用吸波结构材料以提高雷达隐身性能提供参考。

[1]阮颖铮.雷达截面与隐身技术[M].北京：国防工业出版社，1998：55-74. RUAN Yingzheng.Radar section and stealth technology [M].Beijing:National DefenceIndustry Press,1998: 55-74.（in Chinese）

[2]何国瑜,卢才成,洪家才,等.电磁散射的计算和测量[M].北京：北京航空航天大学出版社，2006:192-233. HE Guoyu,LU Caicheng,HONG Jiacai,et al.The calculation and measurement of electromagnetic scatting[M]. Beijing:Beihang University Press,2006:192-233.（in Chinese）

[3]Harrington R F.Time-harmonic electromagnetic fields [M].New York:McGraw-Hill,1968:82-127.

[4]Ruck G T.Radar Cross Section handbook[M].New York:Academic Press,1968:41-69.

[5]Wang J J H.Generalized moment methods in electromagnetics [M].New York:John-Wiley Sons,1991: 113-134.

[6]Knott E,Schaeffer J F,Tuley M T.Radar Cross Section [M].Artech House,Dedham,MA,1985:75-91.

[7]黄培康，殷红成，许小剑，等.雷达目标特性[M].北京：电子工业出版社，2005:24-26. HUANG Peikang,YIN Hongcheng,XU Xiaojian,et al. Radar target characteristics[M].Beijing:Electronic Industry Press,2005:24-26.（in Chinese）

[8]Obelleiro-Basteiro F,Luis R J,BurkholderR J. An interative physical optics approach for analyzing the electromagnetic scattering by large open-ended cavities [J].IEEE TRANS,ANTENNAS PROPAGAT,1995,43 （4）:356-361.

[9]Miller E K,Poggio A J.Moment method techniques in electromagnetic from an application viewpoint.Electromagnetic Scattering[M].New York:Academic Press, 1978:69-73.

[10]Bladel J Van.Electromagnetic fields[M].New York:Mc-Graw-Hill,1964:27-37.

[11]Burkholder R J.A fast and rapidly convergent iterative physical optics algorithm for computing the RCS of open-ended cavities [J].ACES Journal,2001,16（1）: 53-60.

[12]Burkholder R J,Tomas L.Forward-backward iterative physical optics algorition[J].IEEE Trans.On Antenna Propagate,2005,53（2）:793-799.

[13]Mitzner K M.Incremental length diffraction coefficients [R].AircraftDivision No.AFAL-TR-73-296,Northrop: Northrop Corporation,1974.

Numerical Investigation on Electromagnetic Scattering Characteristics for Engine Cavity with Centrocone

YANG Sheng-nan,ZHANG Zhi-xue,SHAO Wan-ren,DENG Hong-wei
（AVIC Shenyang Engine Design and Research Institute,Shenyang 110015,China）

In order to research the effect of centrocone angle and electromagnetic wave incident direction changing on the electromagnetic scattering characteristics of engine cavity,the electromagnetic scattering of engine cavity with centrocone was calculated at 6GHz in C wave band using PO(physical optics)and EEC(equivalent edge currents).The calculation results indicate that the engine cavity with 30°cone angle presents low RCSs in horizontal polarization at θ＝4°～28°;the electromagnetic scattering distribution by engine cavities at angle of interest is given by equivalent currents contour,which provide references to improve stealth capability of engine cavities by taking actions to key areas.

centrocone;engine cavity;radar cross section(RCS);physical optics(PO);equivalent edge currents(EEC);stealth

V 235.1

A

10.13477/j.cnki.aeroengine.2014.01.009

2012-10-16 基金项目：航空科学基金（2011ZA06001）资助

杨胜男（1985）,女,硕士,工程师,从事航空发动机雷达及红外隐身设计技术研究工作；E-mail:yangshengnan@sina.com。

杨胜男，张志学,邵万仁，等.带中心锥航空发动机腔体电磁散射特性数值研究[J].航空发动机，2014，40（1）：48-53，59.YANG Shengnan, ZHANG Zhixue,SHAO Wanren,et al.Numerical investigation on electromagnetic scattering characteristics for engine cavity with centrocone[J]. Aeroengine，2014，40（1）：48-53，59.