概率调整法在气候模式模拟降水量订正中的应用

周 林潘 婕张 镭许吟隆＊

1）（中国农业科学院农业环境与可持续发展研究所农业部农业环境与气候变化重点开放实验室，北京100081）

2）（兰州大学大气科学学院半干旱气候变化教育部重点实验室，兰州730000）

概率调整法在气候模式模拟降水量订正中的应用

周 林1）2）潘 婕1）张 镭2）许吟隆1）2）＊

1）（中国农业科学院农业环境与可持续发展研究所农业部农业环境与气候变化重点开放实验室，北京100081）

2）（兰州大学大气科学学院半干旱气候变化教育部重点实验室，兰州730000）

应用概率调整法订正区域气候模式系统PRECIS在SRES A1B情景下模拟的各季节全国日降水量。以第95百分位降水量为阈值，利用Γ分布分段拟合1962年12月—1972年11月的模拟值，构建传递函数，得到1991年12月—2001年11月的订正值。结果表明：全国平均日降水量空间分布的模拟改善明显，偏差百分率高于100%的格点比例从23.5%降低到1.0%；对各地区平均降水月循环的模拟结果改善，冷季降水较暖季更接近观测，提高拟合优度是改进订正方法的关键；多数地区连续干日数、连续5d最大降水量及极端降水贡献率的空间强度、概率分布与空间相关性的订正效果显著。总体来说，该方法对模拟中国区域降水的平均态与极端降水均有明显改善，有助于气候评估工作的展开。

订正；分段拟合；传递函数；极端降水指标

引 言

气候模式是气候模拟研究以及气候变化影响评估的一种有效工具。全球气候模式的分辨率一般较低，无法准确描述局地气候特征，需要进行统计和动力降尺度。区域气候模式属于动力降尺度，是目前较为常用的区域化手段。通常利用区域气候模式的输出结果作为初始和边界条件驱动区域气候模式，输出具有较高分辨率的结果，从而改善全球气候模式预估未来排放情景下的区域气候响应。研究表明［16］，较高分辨率的区域气候模式对于较好地模拟区域降水非常重要。

模式模拟和观测之间或多或少地存在系统偏差。模式偏差有许多来源，如利用有限变量表征实际大气运动、物理和次网格尺度参数方案以及模式参数选取均会带来不确定性。区域气候模式的模式系统偏差主要来源于其本身以及驱动的全球气候模式的模式偏差，而驱动的全球气候模式所带来的偏差可能是区域气候模式不确定性的主要来源［7］。

应用经验性方法减小模式偏差是一项必不可少的工作，特别是将模式输出变量应用于气候变化影响评估工作中，这与直接改进气候模式并不矛盾［8－9］，是在当前气候模式模拟效果还不十分理想情况下的一种可行选择。如果使用未经订正的模式输出值，则得到的评估结果可能偏离实际［10－12］。

当前偏差后验订正方法主要通过模拟值与观测值建立传递函数。构建传递函数的方法很多［13］，常用的且最为简单的一种订正方法是扰动法（perturbation method），即将模拟得到的气候变化信号，累加到观测值上，作为未来的气候变化情景。如石英等［14］使用这种方法给出了未来华北地区高温事件的分布。扰动法能够改善模拟的平均态，但较难用于日尺度资料订正。而气候预估工作多基于变量分布，因此统计订正方法得到了重视与发展。Piani等［15］提出基于概率分布的经验估计传递函数的订正方法，之后又提出利用模拟值与观测值之间的线性或指数关系构建参数化传递函数［16］；Dosio等［7］将Piani等［15］的参数化拟合订正方法应用于一系列高分辨率模式对气候变化的预测，发现与经验订正法相比，参数化概率拟合偏差订正的结果同样非常有效；Yang等［17］基于变量的概率分布调整构建传递函数，用于订正RCA区域气候模式输出的气温与降水（分别用正态分布、Γ分布拟合），发现欧洲大部分地区各季节不同变量的订正效果都令人满意，改善了气温和降水的平均态、气候变率以及极端降水指标。

本文应用Yang等［17］基于变量概率分布调整的订正方法，订正PRECIS（Providing Regional Climate for Impacts Studies）模式系统［18］输出的日降水量。之前已将这种方法应用于单个格点（上海地区），并对该格点的订正效果进行验证［19］，本文将这一订正方法应用于全国，同时进一步分析订正值极端指标的表现，以验证方法的可行性与适用范围。

1 模式模拟结果

本文使用的区域气候模式模拟数据来自英国Hadley气候预测与研究中心的PRECIS模式系统，是在中国应用较为广泛的区域气候模式之一。已有研究验证了PRECIS模式系统对中国区域气候的数值模拟能力［20－23］。PRECIS模式系统的水平分辨率为0.44°×0.44°，在中纬度地区水平格点间距约为50km；其初始场和边界条件是由低分辨率全球气候模式HadCM3（水平分辨率为纬向3.75°×经向2.5°）提供的。利用温室气体、气溶胶、太阳辐射、火山喷发以及臭氧的历史外在驱动以及IPCC SRES A1B情景的未来温室气体浓度来驱动HadCM3，再以其输出场驱动PRECIS。因此，PRECIS变量输出的偏差不仅包括了其本身的模式偏差、参数化过程所带来的偏差，还包括了HadCM3的偏差。

这里仅以中国区域日降水量的模拟值为例，讨论订正方法的应用。使用的观测资料来自Xie等［24］的1962—2002年东亚日降水观测格点化数据，分辨率为0.5°×0.5°。利用邻近点插值法将模式格点插值到观测数据的格点场，由于本文讨论的是订正方法对模拟值的作用，在此忽略插值所带来的偏差。选取1962年12月—1972年11月为控制时段，1991年12月—2001年11月为订正时段，各10年，两个时段的间隔时间尽可能长，以检验订正方法的有效性。

2 订正与分析方法

对每个格点的日降水量按季节进行订正，12月—次年2月为冬季，3—5月为春季，6—8月为夏季，9—11月为秋季，并将秋、冬季统称为冷季，春夏季统称为暖季。首先，分别将各季节观测值与模拟值按降水强度从小到大进行升序排列，得到如下两组数据：

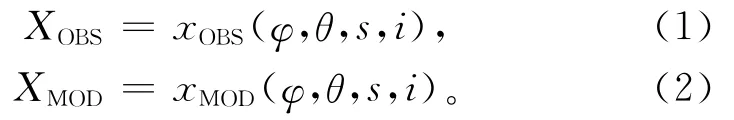
其中，xOBS和xMOD分别为观测和模拟的日降水量，φ和θ分别为格点的经纬度，s表示季节。x（φ，θ，s，i）≤x（φ，θ，s，i＋1），i包括了控制时段或订正时段每个季节的所有日数，大约为900d。对于多数格点模拟降水量，存在一定量的极小偏差降水，将观测的降水日数比例与模拟的总日数相乘即得到订正的降水日数［19］。经降水日数订正后，为构建传递函数形如fφ，θ，s（x（φ，θ，s，i））＝x′（φ，θ，s，i）（x为 模拟值，x′为订正值），本文选择Γ分布分别拟合各季节控制时段观测与模拟降水量的概率分布（式（3）［25］）。

其中，x为日降水量，α为形状参数，β为尺度参数，xp为某一特定的日降水量。Γ分布是目前常用来描述日降水量的概率分布，这是因为其对日降水量的 描 述 有 较 高 的 稳 定 性［25］。 经 Kolmogorov－Smirnov检验［26］，Γ分布对全国半数格点四季日降水量的分布拟合达到0.01显著性水平。考虑到日降水量概率分布的强偏斜于小降水值，选取第95百分位降水量为极端降水阈值，采用分段拟合的方法。

阈值确定采用Bonsal等［27］的方法，即将具有n个值的某气象要素按升序排列x1，x2，…，xm，…，xn后，某个值不大于xm的概率为

其中，m为xm的序号。如有30个值，第95个百分位上的值为排序后的x29（P＝94.4%）和x30（P＝97.7%）的线性插值。

通过两个数据段检验（显著性水平为0.01）的格点数相较于整体拟合均显著提高（远超过半数），同时，超过90%的格点通过极端降水拟合检验。因此，分布分段拟合能够显著提高对中小降水值以及极端降水的分布拟合能力。

根据极大似然估计法，Γ分布的形状参数α和尺度参数β的似然方程［25］为

Thom 等［28］推得的估算式为

其中，αOBS，βOBS与αCTL，βCTL分别为控制时段第95百分位以下观测值和模拟值的参数估算，αOBS，95th，βOBS，95th与αCTL，95th，βCTL，95th则为第95百分位以上观测值与模拟值的参数估计，x和x′分别为日降水量的模拟值和订正值，x95th为控制时段第95百分位的模拟值。

前面的研究工作已经证明该订正方法对上海单格点的订正效果比较有效［19］，这里将订正方法应用到全国区域，以检验其有效性。本文不仅检验订正方法对平均态的订正能力，同时还检验其对极端降水的订正能力，选取了3个极端降水指标，分别为连续干日数、连续5d最大降水量以及极端降水贡献率。连续干日数指一年中日降水量小于1mm的最大连续日数；连续5d最大降水量指一年中连续5d降水量之和的最大值；极端降水贡献率指一年中极端日降水量（订正时段每年第95百分位降水量的10年平均值作为极端降水阈值，大于该阈值的日降水量定为极端日降水量）之和与该年年降水量的比值。同时，利用空间相关系数R来定量比较模拟与订正的区域极端降水指标与观测的相似程度［25］：

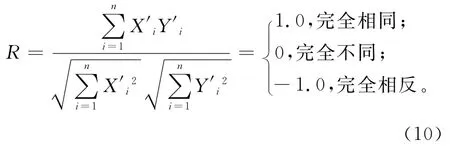
其中，n为格点数，X′i是第i个格点的模拟或订正距平值，Y′i则为相应的观测距平值。R越接近1，说明区域极端降水指标的模拟值或订正值越接近观测值。

3 订正效果

3.1 平均态订正能力

［29］本研究将全国划分为8个区域（图1）。PRECIS模式系统基本模拟出了日平均降水量西北小、东南大的空间分布，同时在青藏高原东南地区存在一个降水大值区（图2a）。但模拟值存在较大偏差（图2b～2c），其主要特征为湿偏差（全国平均偏差为0.58mm），主要集中在东北、内蒙古北部至青藏高原，呈东北—西南分布，严重湿偏差区位于青藏高原西部及其与新疆交界地区，偏差百分率最大可达1720%；干偏差主要位于新疆大部分地区、华东以及华南地区，严重干偏差区位于准噶尔盆地和吐鲁番盆地，偏差百分率最大可达90%。可以看出，降水的大偏差区主要位于地形环境比较复杂的地区，且在地势高区容易出现湿偏差，地势低区容易出现干偏差。仅四川盆地出现了湿偏差。

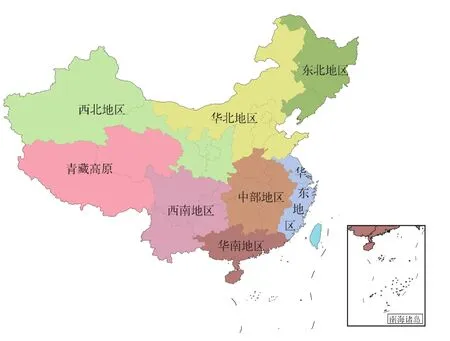
图1 本研究中区域划分Fig.1 Classification in this study

Γ分布分段拟合订正法对平均降水空间分布的订正非常显著（图2d～2e），特别是对偏差大值的订正。严重偏差的区域不变，但范围减小，且湿、干偏差百分率最大分别减小到270%，40%。订正后，全国平均降水偏差从0.58mm减小到0，偏差百分率小于10%的格点数占全国总格点数的比例从12.3% 提高到44.9%，高于100%的格点比例从23.5%降低到1.0%。

由于所用方法基于季节进行订正，订正值对平均降水的逐月分布有非常显著的改善（图3）。8个区域的订正值均更接近观测值，特别是西南与青藏高原地区。冷季订正值均较暖季更接近于观测值，暖季订正值改善显著，但仍存在一定偏差，如华东、华南以及中部地区6月订正后的平均降水量虽然有所改善，但仍然存在较大的干偏差；东北与西北地区6月订正后的平均降水量甚至存在过订正。这是由于暖季强降水更多，降水强度变化较大，这给概率分布拟合带来一定的不确定性，而暖季降水的概率分布拟合是改进暖季降水订正的关键。

总体来说，Γ分布分段拟合订正法可以显著改善模拟的全国区域平均降水量的空间分布，以及各区域平均的降水量变化。因此，该方法对模式模拟降水平均态的订正能力值得肯定。

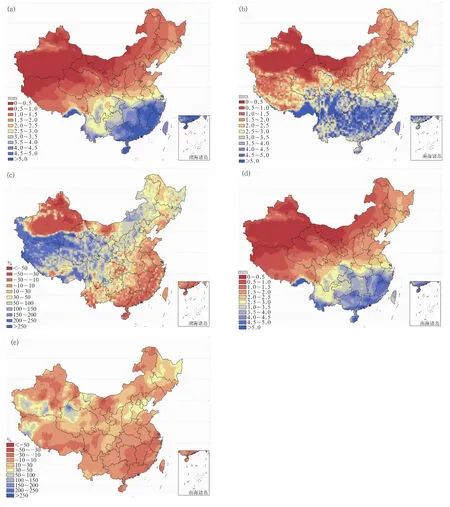
图2 订正时段观测、模拟及订正的中国区域日平均降水量的空间分布及其偏差百分率（a）观测值的空间分布，（b）模拟值的空间分布，（c）模拟值的偏差百分率，（d）订正值的空间分布，（e）订正值的偏差百分率Fig.2 Spatial distribution of observed，simulated and corrected mean precipitation and the bias percentage over China in correction period（a）spatial distribution of the observed，（b）spatial distribution of the simulated，（c）the bias percentages of the simulated，（d）spatial distribution of the corrected，（e）the bias percentages of the corrected

3.2 极端降水订正能力

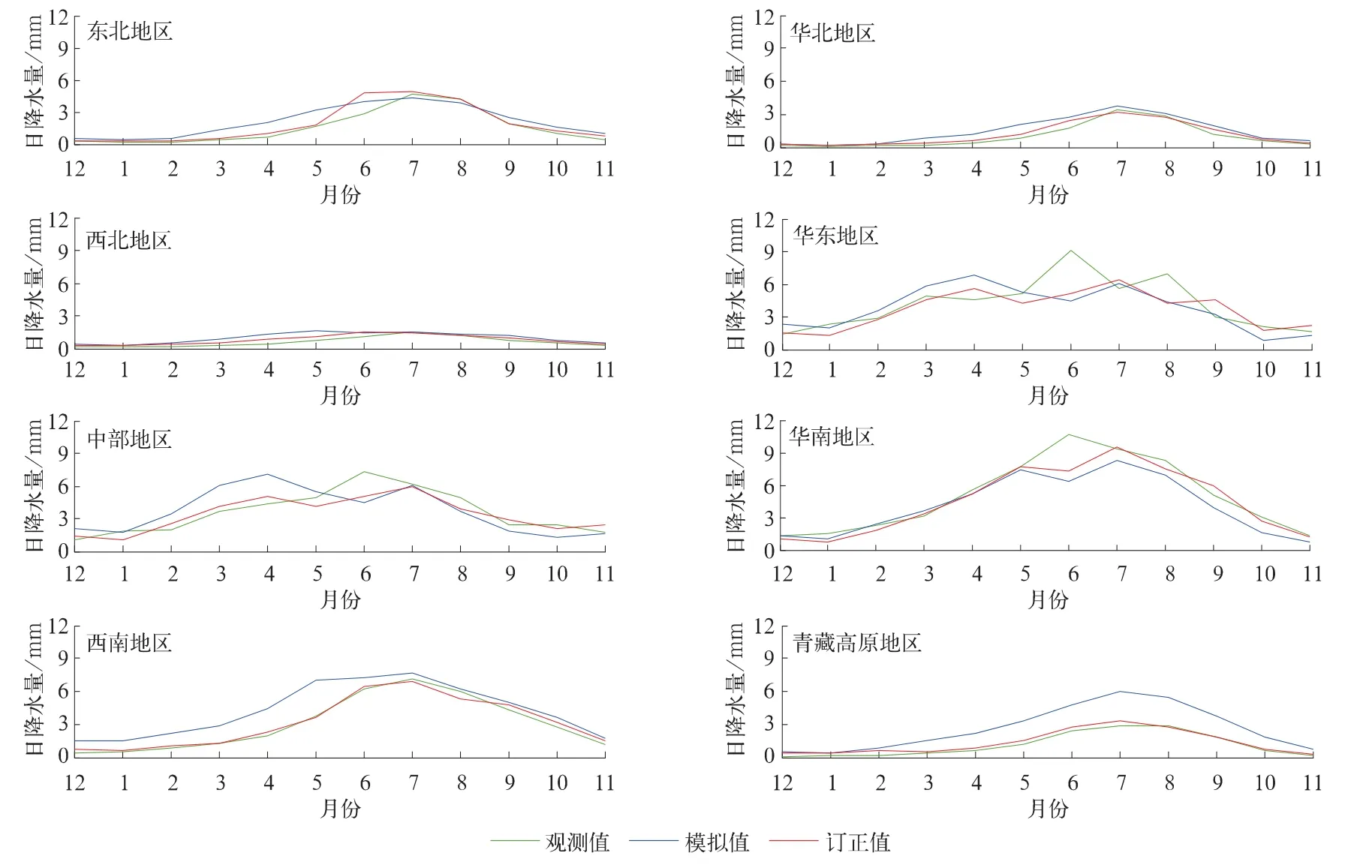
图3 订正时段观测、模拟及订正的各区域平均降水量Fig.3 The observed，the simulated and the corrected region－averaged precipitation in correction period

在本节的讨论中，只关注不小于1.0mm的日降水量。图4～图6分别给出了订正时段观测、模拟及订正的连续干日数、连续5d最大降水量及极端降水贡献率在中国区域的空间强度分布，且图7给出了其概率分布，为清晰起见，图7中没有显示出连续干日数与连续5d最大降水量低概率的大值部分。表1给出了模拟及订正的与观测的各区域平均极端指标空间相关系数。

图5 同图4，但为连续5d最大降水量的空间分布Fig.5 The same as in Fig.4，but for the spatial distribution of maximum 5－day precipitation amount

中国区域10年平均的连续干日数观测值为68d，模拟值略偏小，为63d，订正值反而增大到74d。从空间分布来看（图4），模拟值更接近观测的空间分布，特别是对青藏高原、华北北部的负偏差以及西南、西南北部的正偏差的改善。同时从概率分布（图7）来看，订正后，概率分布与观测非常接近，而模拟的概率分布主要表现为低值与高值偏多，特别是小于50d的连续干日数值概率显著偏大，观测、模拟及订正的最大值分别为213d，362d，227d。此外，从各区域的空间相关系数（表1）来看，模拟的连续干日数空间分布相关性以华北地区最高，中部地区最低；订正后各地区的空间相关性显著提高，其中相关性改善程度中部地区最大，华北地区最小。

中国区域10年平均的连续5d最大降水量观测值为77mm，模拟值显著偏大，为96mm，订正后减小到87mm。同时对空间分布也有较大改善（图5），特别是对青藏高原与华南地区连续5d最大降水量偏差的改善。然而也应注意到西北地区存在一定范围的过订正。订正后，全国概率分布上相较于模拟值更加接近观测（图7）。20mm以下的连续5d最大降水量模拟值偏大，订正值接近于观测值；20～50mm的连续5d最大降水量存在过订正，模拟值较接近于观测值；50mm以上的连续5d最大降水量订正值更接近于观测值，但仍具有一定的正偏差。总体来说，该订正方法能够有效改善模拟连续5d最大降水量偏大的特征。模拟值的空间相关性以西北地区最高，中部地区最低；订正后除华东地区外均有显著提高，其中相关性改善程度西南地区最大，东北地区最小（表1）。

中国区域10年平均的极端降水贡献率观测值为21%，模拟值与订正值均为22%。空间分布上（图6），极端降水贡献率基本呈现西部低、东部高的趋势。模拟值基本表现出了这一分布特征，订正后西北地区的负偏差以及东部地区（特别是东北、华北）的正偏差有所减小，不过对青藏高原西部以及西北部分地区存在过订正。观测、模拟及订正的概率分布均呈正态分布，且模拟值本身已经比较接近观测值，订正后除在23%～25%之间存在明显的过大订正外，有不同程度的订正（图7）。模拟值的空间相关性普遍较差；订正后除东北与青藏高原地区外均有提高，其中西南地区相关性改善程度最大，华北地区改善最小，但相关性相较前两个指标更差（表1）。

图6 同图4，但为极端降水贡献率的空间分布Fig.6 The same as in Fig.4，but for the spatial distribution of extreme precipitation contribution

图7 订正时段中国区域连续干日数、连续5d最大降水量及极端降水贡献率的概率分布Fig.7 The observed，the simulated and the corrected probability density distributions of consecutive dry days，maximum 5－day precipitation amount and contribution of extreme precipitation over China in correction period

表1 订正时段模拟及订正与观测的各区域平均极端指标空间相关系数Table 1 Spatial correlation coefficient of region－averaged extreme index derived from the simulated and the corrected to the observed precipitation in correction period

综上，模拟的3种极端降水指标与观测较为接近，但仍存在一定偏差。Γ分布分段拟合订正法对3种指标的订正能力均得到验证，无论是从空间强度分布、概率分布以及各地区的空间相关系数上，均有显著改善。因此，该方法对模式模拟极端降水的订正能力值得肯定。

4 结论与讨论

本文在前面研究工作［19］的基础上，将基于Γ分布分段拟合的偏差订正方法应用于PRECIS模式系统在A1B排放情景下的日平均降水量模拟结果，按季节构建传递函数进行订正。与整体拟合相比，分段拟合能够有效改善对中、小降水量以及极端日降水值的拟合能力。对降水平均态以及极端降水指标连续干日数、连续5d最大降水量、极端降水贡献率的分析表明：

1）模式基本模拟出了降水平均态以及极端降水指标的空间分布，但存在一定偏差，偏差大值区主要位于地形复杂地区，地势高区易出现湿偏差，地势低区易出现干偏差，四川盆地为湿偏差大值区。

2）订正方法对全国区域平均降水量的空间分布有显著改善，特别是对偏差大值的订正。偏差百分率小于10%的格点数占全国总格点数的比例从12.3% 提高到44.9%，高于100%的格点比例从23.5%降低到1.0%。

3）全国各地区平均的降水量得到有效订正，其中，西南与青藏高原地区订正后与观测几乎一致。冷季订正的降水比暖季更接近于观测，6月平均降水量在华东、华南以及中部地区仍有较干偏差，而东北与西北地区甚至存在过大订正，这是由于暖季降水强度变化较大且强降水频数与强度更大，给概率分布拟合带来一定的不确定性。因此，如何更好地拟合暖季降水的概率分布是改进暖季、甚至全年降水订正的关键环节。

4）订正方法可显著改善模拟的全国区域极端降水指标。无论从空间强度、概率分布以及空间相关性上，模拟的3个指标均有显著改善。订正后除华东地区的连续5d最大降水量、东北与青藏高原地区的极端降水贡献率相关性出现过订正外，其余地区3个指标的相关性均有提高。

本文所用订正方法基于模式与观测变量的概率分布偏差不随时间变化的假设前提下，Ho等［30］将这种订正思路归为偏差订正，同时提出另一种订正思路，即变率订正，是基于模式完美模拟出观测变量的变化的假设，并以HadRM3对欧洲的温度输出为例讨论了两种不同订正方法得出的增暖空间分布有所不同，但无法确定哪种订正方法应用于影响评估更有效。Hawkins等［31］认为变率订正方法较偏差订正方法更稳健，同时指出这一结论需要得到欧洲以外区域、不同气候变量以及不同模式的证明。这两种订正思路在本质上一致，差别在于模式的模拟能力更偏向于哪一种假设，不同的模式可能会有不同的结果。但可以肯定的是，无论哪种方式，都能够对模式结果有明显改善。哪种方法更适用于PRECIS模式系统输出的气候情景，需要更多的研究工作。

致 谢：感谢英国Hadley气候中心提供PRECIS模式系统，同时感谢中国科学院大气物理研究所涂锴博士在本论文完成过程中给予的帮助。

参考文献

［1］ 刘永强，丁一汇.区域气候模拟研究.应用气象学报，1995，6（2）：228－239.

［2］ 高学杰，赵宗慈，丁一汇，等.温室效应引起的中国区域气候变化的数值模拟.第一部分：模式对中国气候模拟能力的检验.气象学报，2003，61（1）：20－28.

［3］ 李维京，张培群，李清泉，等.动力气候模式预测系统业务化及其应用.应用气象学报，2005，6（3）：1－11.

［4］ 刘一鸣，丁一汇，李清泉，等.区域气候模式对中国夏季降水的10年回报试验及其评估分析.应用气象学报，2005，16（3）：41－47.

［5］ 高学杰，徐影，赵宗慈，等.数值模式不同分辨率和地形对东亚降水模拟影响的试验.大气科学，2006，30（2）：185－192.

［6］ Yu E T，Wang H J，Sun J Q.A quick report on a dynamical downscaling simulation over china using the nested model.Atmos Oceanic Sci Lett，2010，3（6）：325－329.

［7］ Dosio A，Paruolo P.Bias correction of the ENSEMBLES highresolution climate change projections for use by impact models：Evaluation on the present climate.J Geophys Res，2011，116，D16106.

［8］ 李莉，朱跃建.T213降水预报订正系统的建立与研究.应用气象学报，2006，17（2）：130－134.

［9］ 任宏利，丑纪范.数值模式的预报策略和方法研究进展.地球科学进展，2007，22（4）：376－385.

［10］ Wood A W，Leung L R，Sridhar V，et al.Hydrologic implications of dynamical and statistical approaches to downscaling climate model outputs.Climatic Change，2004，62（1－3）：189－216.

［11］ Baigorria G A，Jones J W，Shin D W，et al.Assessing uncertainties in crop model simulations using daily bias－corrected regional climate model projections.Climate Research，2007，34：211－222.

［12］ Ghose S，Mujumdar P P.Climate change impact assessment：Uncertainty modeling with imprecise probability.J Geophys Res，2009，114，D18113.

［13］ 宋超辉.不同数学模型在降水量资料序列订正中适用性探讨.应用气象学报，1998，9（2）：213－218.

［14］ 石英，高学杰，吴佳，等.华北地区未来气候变化的高分辨率数值模拟.应用气象学报，2010，21（5）：580－589.

［15］ Piani C，Haerter J O，Coppola E.Statistical bias correction for daily precipitation in regional climate models over Europe.Theor Appl Climatol，2010，99（1－2）：187－192.

［16］ Piani C，Weedon G P，Best M，et al.Statistical bias correction of global simulated daily precipitation and temperature for the application of hydrological models.J Hydrol，2010，395（3－4）：199－215.

［17］ Yang W，Johan A，Phil G L，et al.Distribution－based scaling to improve usability of regional climate model projections for hydrological climate change impact studies.Hydrology Research，2010，41（3－4）：211－229.

［18］ Jones R G，Noguer M，Hassell D C，et al.Generating High Resolution Climate Change Scenarios Using PRECIS.Met Office Hadley Centre，2004.

［19］ 周林，潘婕，张镭，等.气候模拟日降水量的统计误差订正分析——以上海为例.热带气象学报，2014，30（1）：137－144.

［20］ 许吟隆，Richard Jones.利用ECMWF再分析数据验证PRECIS对中国区域气候的模拟能力.中国农业气象，2004，25（1）：5－9.

［21］ 许吟隆，黄晓莹，张勇，等.PRECIS对华南地区气候模拟能力的验证.中山大学学报：自然科学版，2007，46（5）：93－97.

［22］ 田红，许吟隆，林而达.温室效应引起的江淮流域气候变化预估.气候变化研究进展，2008，4（6）：357－362.

［23］ 王芳栋，许吟隆，李涛.区域气候模式PRECIS对中国气候的长期数值模拟试验.中国农业气象，2010，31（3）：327－332.

［24］ Xie P P，Chen M Y，Song Y，et al.A gauge－based analysis of daily precipitation over east Asia.J Hydrometeorology，2007，8：607－626.

［25］ 么枕生，丁裕国.气候统计.北京：气象出版社，1990：68－170.

［26］ Durbin J.Distribution Theory for Tests based on the Sample Distribution Function.Society for India and Applied Mathematics，1973.

［27］ Bonsal B R，Zhang X，Vincent L A，et al.Characteristics of daily and extreme temperature over Canada.American Metrological Society，2001，5（14）：1959－1976.

［28］ Thom H S.A note on the Gamma distribution.Mon Wea Rev，1958，86（4）：117－122.

［29］ 姜彤.适应行动：数据及风险分析.专题研讨一：适应气候变化的共性问题∥适应气候变化——东亚峰会成员国的战略、政策与行动.北京：科学出版社，2009.

［30］ Ho C K，Stephenson D B，Collins M，et al.Calibration strategy：A source of additional uncertainty in climate change projections.Bull Amer Meteor Soc，2012，93：21－26.

［31］ Hawkins E，Osborne T M，Ho C K，et al.Calibration and Bias Correction of Climate Projections for Crop Modelling：An Idealised Case Study Over Europe.Agricultural and Forest Meteorology，2012.http：∥dx.doi.org／10.1016／j.agrformet.2012.04.007.

Correction Based on Distribution Scaling for Precipitation Simulated by Climate Model

Zhou Lin1）2）Pan Jie1）Zhang Lei2）Xu Yinlong1）2）

1）（Institute of Environment and Sustainable Development in Agriculture，Chinese Academy of Agricultural Sciences，Beijing100081）
2）（Key Laboratory or Semi－arid Climate Change of the Ministry of Education，College of Atmospheric Sciences，Lanzhou University，Lanzhou730000）

A statistical bias correction based on piecewiseΓdistribution fitting to construct seasonal transfer function is applied to the precipitation simulated by a regional climate model PRECIS under the SRES－A1B emission scenario over China.The transfer function（TF）is derived from the control period of December 1962—November 1972，fitting the cumulative probability density function of both simulated and observed precipitation withΓdistribution.The 95th percentile precipitation is chosen to be the threshold and precipitation below and upon the threshold are fitted，respectively.When compared with wholesale fitting，this method can better fit the distributions of both small／medium precipitation and extreme precipitation.Then the TF is applied for the validation period of December 1991－November 2001.The correction strategy is based on the assumption that discrepancies between model and observation stay constant with time.

Results show that PRECIS can reproduce the spatial distribution of mean and extreme precipitation，while the biases exist.The biases are larger if the topography is more complex.If the region is high or low in altitudes，the bias tends to be positive or negative，while Sichuan Basin is the exception，where large positive biases occur.

The correction based on the piecewiseΓdistribution fitting can well correct the spatial distribution of the mean precipitation over China，especially over the original large－bias regions，and the grids in which the bias percentages used to be larger than 100%are reduced from 23.5%down to 1.0%.Simulation of region－averaged monthly precipitation is significantly improved，especially over Southwest China and the Tibet Plateau regions.Precipitation in cold seasons is better corrected，while it has relatively larger biases in warm seasons especially in June due to a wide range of precipitation，which may bring difficulties during fitting.So，it’s crucial to improve the fitting probability in warm seasons.

The piecewiseΓdistribution fitting correction also does a quite good job in correcting the extreme precipitation.The spatial distribution，probability density distribution and spatial correlation coefficient of consecutive dry days，the maximum 5－day precipitation amount and the contribution of extreme precipitation are corrected significantly，except for maximum 5－day preciptiation amount in East China，contribution of extreme precipitation in Northwest China and the Tibet Plateau are overcorrected.These show that the technique has the ability to correct the extreme precipitation.

In general，the correction results are satisfying，which implies that the piecewiseΓdistribution fitting correction is capable of improving the reproduction of both mean and extreme precipitation simulated by regional climate model PRECIS over China，which is useful for assessment research.

correction；piecewise fitting；transfer function（TF）；extreme precipitation index

周林，潘婕，张镭，等.概率调整法在气候模式模拟降水量订正中的应用.应用气象学报，2014，25（3）：302－311.

2013－10－26收到，2014－02－18收到再改稿。

国家科技支撑计划项目（2013BAC09B04，2012BAC19B10），中－英－瑞（士）中国适应气候变化项目之国家水平的气候变化自然影响和风险评估课题

＊通信作者，email：xuyl＠ami.ac.cn