地方政府与中央政府之间的投资博弈分析
●翟金宝 郑亚迪
地方政府与中央政府之间的投资博弈分析
●翟金宝 郑亚迪
针对地方政府之间存在的竞争加合作、竞争大于合作的博弈关系,建立了不完全信息条件下中央政府介入前后地方政府投资博弈模型,该模型揭示出地方政府行政性重复建设、短期性投资等低效率行为的原因。模型还显示在中央政府在税收和补贴政策的调控下,中央预期投资收益会增加,地方政府之间的重复投资率降低幅度较大。
地方政府 中央政府 投资博弈
一、引言
在中国行政体系中,地方政府数目众多,且地方政府之间存在一定的竞争加合作、竞争大于合作的博弈关系。地方政府的这种数量和行为特征,为评价和比较地方政府公共投资效率奠定了一定的理论基础。事实上,在中国传统体制条件下,地方政府之间的利益博弈是间接的、潜意识的和低层次的,但随着市场体制的不断建立,经济资源的地区流动不断增强,地方政府之间的利益博弈就有了直接、显性和全面化的特质,其中,加强本地区公共投资、改善投资环境往往就成为各地方吸引外部资源并提高本地区经济竞争力的重要手段。
二、中央政府介入前地方政府之间的投资博弈模型
博弈分析的前提假设有:
1.各地方政府在区域性产业结构和投资调整过程中的决策信息是不完全的。也就是说,作为投资主体的地方政府对其投资于某产业的预期成本与预期收益的信息是充分的,而对其他地方政府投资的预期成本与预期收益的信息是不充分的。
2.选择A和B分别代表两个地方政府,欲投资建设的两个项目分别属于经济效益较低的基础产业和经济效益较高的非基础产业。
3.受到地方财政投资资金的有限性约束,A和B两个地方政府各自只能进行某一种产业投资,且相应的产品生成在两地之间基本是无差异的。
4.由于A、B两地的资源、生产技术、投资成本等方面的差异,A地方政府在基础产业方面更有相对优势,而B地方政府在非基础产业更有相对优势。
5.短期内非基础产业比基础产业更有利于地方经济效益的最大化,所以地方政府更倾向于投资营利性行业。
在上述基本假设条件下,A、B两个地方政府的投资博弈可用标准博弈形式表示如下,表格内的数字分别表示局中人在不同博弈策略组合下可能的投资收益。

表1 地方政府与地方政府之间的投资博弈模型标准形式
显然,上述地方政府投资博弈模型不存在“优超策略均衡”,却存在两个“纳什均衡”,分别为策略组合(非基础产业,基础产业)和(基础产业,非基础产业)。由于局中人的有限理性和信息不对称,每个地方政府对其他局中人的行为策略和支付函数并不完全了解,但可以测算相应的概率分布值。设A地方政府以α的概率选择非基础产业,以1-α的概率选择基础产业投资;B政府以β的概率选择非基础产业,以1-β的概率选择基础产业投资。于是,A地方政府的预期收益函数为:

满足地方政府A的投资期望收益最大,即Max EA(α,β)的一级最优条件为:

同理,地方政府B的投资期望收益函数可表示为:

满足地方政府B的投资期望收益最大,即Max EB(α,β)的一级最优条件为:

基于算出的概率参数α和β值,地方政府投资期望最大值为:

基于上述分析,代表全国整体利益的中央政府最大期望收益值为:

P(非基础产业,非基础产业)=P{地方政府A选择非基础产业投资}*P{地方政府B选择非基础产业投资}=1014*1517=51. 90%
P(非基础产业,基础产业)=P{地方政府A选择非基础产业投资}*P{地方政府B选择基础产业投资}=1014*217=6.92%
P(基础产业,基础产业)=P{地方政府A选择基础产业投资}*P{地方政府B选择基础产业投资}=414*217=2.77%
P(基础产业,非基础产业)=P{地方政府A选择基础产业投资}*P{地方政府B选择非基础产业投资}=414*1517=20.76%
根据上述计算结果,非重复投资率为:p两地非重复投资=p(非基础产业,基础产业)+p(基础产业,非基础产业)=27.68%
显然,上述分析说明:在各地方政府追求本辖区短期利益最大化的情况下,各地方政府在非基础等营利性产业进行重复建设的概率最大。这解释了地区间政府行为推动的重复投资和产业结构同质化问题的背后原因,也解释了各地方政府较为普遍存在的公共基础设施建设方面的历史“欠债”问题。
三、中央政府介入后的地方政府之间投资博弈模型
中央政府通过对高盈利的非基础产业投资征税(税额t),与此同时,对地方基础产业投资予以补贴(补贴额为s),以改变地方政府的收益矩阵,从而纠正和解决地区间的重复性投资建设问题。假设征税额t等于补贴额s(即对营利性产业投资征收的税收完全的用于补贴基础性产业投资)。在此情况下,可以证明:当t为一定取值时,就会使得地区间低水平重复性投资率有所减低。设想中央政府通过税收和补贴政策来致力于解决地区间重复投资率过高的问题,且征收额t等于补贴额s,中央政府介入后的地方政府之间投资博弈收益矩阵则为:

表2 中央政府介入后地方政府之间的投资博弈模型标准形式
假设A地方政府仍以α的概率选择非基础产业,以1-α的概率选择基础产业投资;B政府以β的概率选择非基础产业,以1-β的概率选择基础产业投资,则地方政府A和地方政府B的投资期望收益函数分别为:

代表全国总利益的中央政府最大期望收益值为:
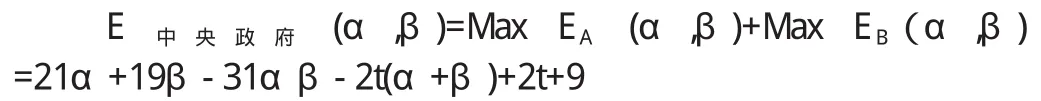
在地方政府A和地方政府B都追求地区经济最大化的情况下,于是求解中央政府预期收益极限问题就可转化为:
目标函数:Max E中央政府(α,β)=21α+19β-31αβ-2t (α+β)+2t+9

约束条件:

通过拉格朗日乘数求Max E中央政府极值,于是有:α=35.30%,β=66.33%,t=2.19,将上述计算结果带入中央政府期望收益函数,则有:

上述结果表明,在一定的税收和补贴政策作用下,两个地方政府的预期收益之和不仅没有减低,反而比中央政府实行调控政策之前的预期收益之和有所增加。在上例中,两地预期投资收益总和较之前增加了2.17%。再考虑宏观调控政策之下两地重复投资率的变化情况,于是有:
在中央政府实行收益补偿政策下,地方政府A和地方政府B之间的重复投资率为:p*两地重复投资=p*(非基础产业,非基础产业)+p*(基础产业,基础产业)=35.30%*65.33%+64.70% *34.67%=45.49%<54.67%
四、结论
可见,由于没有总体的利益协调机制和完善的法律法规约束,地方政府为实现本地区利益最大化往往会舍弃地方间分工协作而产生的整体效益最优。但如前分析,在中央政府的税收和补贴政策的纠正作用下,不仅中央预期投资收益不会减少,而且地方政府A和地方政府B之间的重复投资率也会有原来的较高水平(即54.67%)降至较低水平(即45.49%),重复投资的降低幅度高达16.79%。从而在很大程度上克服了地区产业结构同质化等的问题。
[1]张迎伟.博弈论与信息经济学[M].上海人民出版社,1996(2)
[2]钱颖一.现代经济学与中国经济改革[M].中国人民大学出版社,2003(8)
[3]胡荣涛.产业结构与地区利益分析[M].经济管理出版社,2001(7)
[4]钟成勋.地方政府投资行为研究[M].1993
[5]李小华.西部地区产业结构的优化模型[J].重庆工商大学学报,2003(3)
(作者单位:翟金宝,山西唐一能源科技有限公司 山西晋城 048000;郑亚迪,渭南职业技术学院 陕西渭南 714000)
(责编:贾伟)
F830
A
1004-4914(2014)04-074-02

