基于有限体积法的平面二维水流数学模型的改进
李绍武,张弛,杨学斌,李文善
(天津大学水利工程仿真与安全国家重点实验室,天津300072)
基于有限体积法的平面二维水流数学模型的改进
李绍武,张弛,杨学斌,李文善
(天津大学水利工程仿真与安全国家重点实验室,天津300072)
在基于有限体积法的近岸水流数学模型中,单元交界面数值通量的计算精度、潜堤淹没和出露交替的模拟以及动边界技术都是至关重要的。首先通过加入数值通量底坡补偿项对Osher格式的数值通量计算格式进行了改进;又提出单元淹没度的概念,提高了模型在模拟潜堤出露和潮间带干湿变化中的适应性。利用典型算例对模型进行了验证,得到了满意的结果。
水流数学模型;底坡补偿项;有限体积法;潜堤;淹没度;动边界
基于有限体积法的水流数学模型的精度在很大程度上取决于单元交界面数值通量计算格式的精度。有限体积法计算格式大都将主要变量定义在单元中心,由于变量定义点的错位,难免造成界面数值通量计算产生一定数值误差,这种误差在时间步进中不断积累,将影响计算精度和格式稳定性。另一方面,将水流数学模型运用于潮汐河口或缓坡海域时,需要对活动边界进行处理。目前常用的干湿网格法、水边线步进法、窄逢法和井点法等[1-2]都有一定局限性,如干湿网格法和水边线步进法中边界的干湿变化以一个网格为单位更替,精度取决于网格大小;窄逢法和井点法虽然精度较高,但数值稳定性稍差。数学模型在近岸应用中的另一个问题是潜堤出露给建模带来的困难。结合有限体积数值求解方法[3-5],首先提出一种交界面数值通量计算精度的改进方法,导出了相关计算公式;然后,针对活动边界和潜堤出露问题,提出了淹没度的概念,即将所有单元(包括内单元、水陆交界单元和陆单元)都视为具有不同淹没度的网格单元。控制方程在所有单元上进行统一离散,从而使变量在水、陆单元之间可以连续过渡,计算更为简便,精确度有一定提高。
1 平面二维浅水波数学模型的控制方程
1.1 控制方程
近岸潮波运动二维浅水波方程包括质量守恒方程和动量守恒方程。
质量守恒方程

x方向动量守恒方程

y方向动量守恒方程
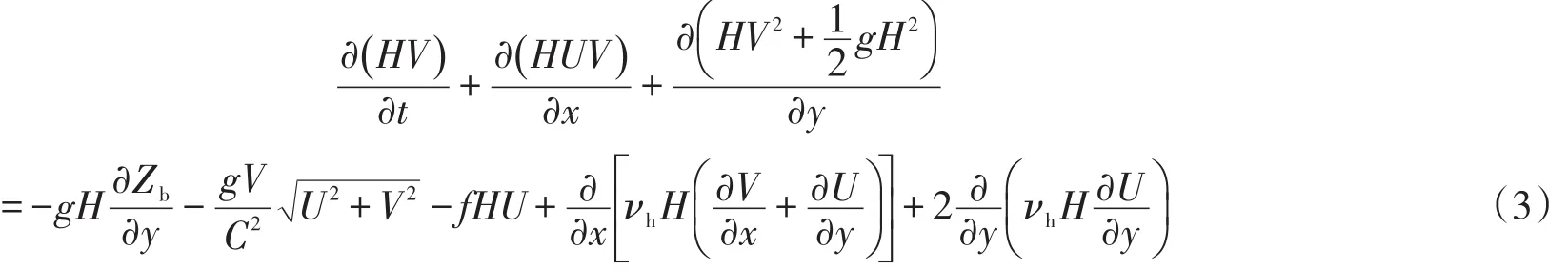
式中:H为全水深;U、V分别为垂向平均流速的x、y方向分量;g为重力加速度;Zb为底高程;C为谢才系数,可由曼宁公式计算,其中n为曼宁糙率系数;f为科氏参数,f=2Ωsinϕ,Ω为地球的自转频率,Ω=2π/86 164,ϕ为当地纬度;νh为水平方向上的紊动粘滞系数,由Smagorinsky亚格子紊动模型得到,即

式中:cs=0.1~0.2;Δs为离散单元面积。
1.2 初始条件
初始水位按η=η0(x,y)给定,初始速度按0给定。
1.3 边界条件
固边界采用“不穿透”边界条件,即V×n=0,其中V为流速矢量,n为沿固边界外法线方向的单位矢量。开边界处给定水位过程η=ηb(x,y,t)。
2 控制方程的数值求解方法
2.1 有限体积法计算格式
根据有限体积法的求解思路[5],将控制方程写为向量形式

式中:U=H(1,U,V)T为守恒物理量向量,F=(HU,HU2+gH2/2,HUV)T为x方向上的通量,G=(HU,HUV,HV2+ gH2/2)T为y方向上的通量为右端项,其中的Fb、Ff、Fc和Ft分别代表底坡项、底摩阻项、科氏力项和紊动掺混项。
对式(5)在单元体上进行积分,并应用格林公式,得到

式中:U͂为转换到交界面局部坐标下的状态变量。
定义单元第j条边的边长为Lj,U͂和V͂分别为局部坐标系下状态变量的分量,h(l)为单元边上的水深变化函数,则单元数值通量计算公式为
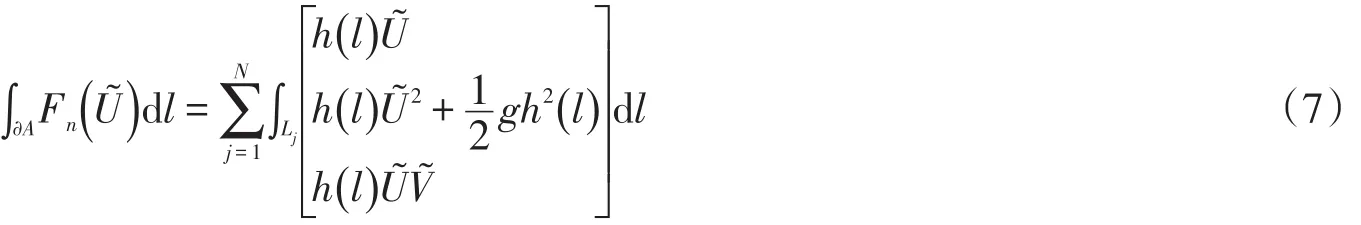
假设h(l)沿单元边线性变化,且单元边两端点的底高程差为ΔZj,hˉsj为第j条边的平均水深,则可以导出数值通量计算公式为

式(6)采用时间向前差分即可进行显式求解。
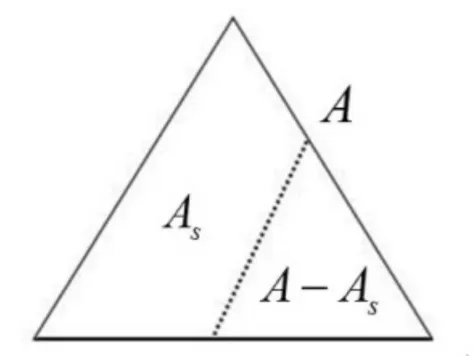
图1 有效单元示意图Fig.1 Sketch of an effective element
2.2 淹没度概念
假设任意多边形单元面积为A,被水淹没的部分面积为As(图1),定义淹没度αs=As/A[6],该量表示单元中淹没部分与全部面积的比值,可以表征单元的干湿状态。
显然,当αs=0时,网格处于全干状态;当αs=1时,As=A,网格处于全淹状态;当0<αs<1时,单元处于半干半淹状态。
对于任意淹没度(0<αs≤1)的单元,单元水体体积为

式中:Vw为单元中被水淹没部分的水体积。
假设某单元3个节点的底高程从小到大依次为Z1,Z2,Z3,根据三角单元的淹没情况,可能出现以下4种情形。
情形一:当η≤Z1时,αs=0,Hs=0。
情形二:当Z1≤η≤Z2时,单元仅一个节点被淹没,淹没部分仍然为三角形,淹没度此时,平均水深
情形三:当Z2≤η≤Z3时,淹没度平均水深为
情形四:当η≥Z3时

图2 计算区域水位及地形纵剖面图Fig.2Longitudinal profile of computational domain
3 水流模型的验证
以下通过具体算例讨论模型的适用性。
3.1 恒定水位算例
为了考察通量补偿项的影响效果,构造尺寸为500 m-250 m的非平底模型(图2和图3),底部糙率为0.02,计算区域上下边界为固边界,左右为开边界,水位保持10 m不变。计算稳定后,沿x轴方向剖面水位变化如图4所示,结果表明,缺少补偿项将会在底坡度变化处引起显著误差,且误差有振荡,最大达到0.003 m,而在两侧的平底处误差为0,而这正是引入底坡补偿项的效果。

图3 计算区域地形平面及网格剖分图Fig.3Topography and gridding of computational domain

图4 有无补偿项计算结果对比Fig.4Comparison of numerical results of water surface elevation for the cases with and without ompensational term
3.2 均匀底坡上的圆形浅滩算例
计算区域为一5000m×2500m的矩形斜底水槽,底部糙率为0.02,中心设一球冠,半径为673 m,其底高程由以下方程给出(图5)。
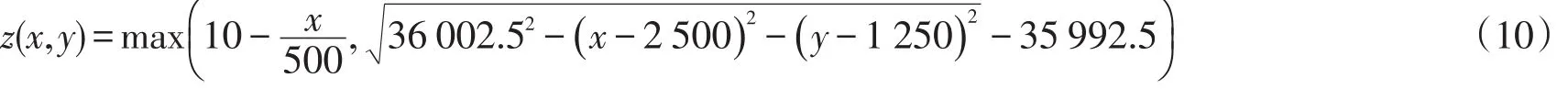
模型上下两侧设置为固边界,左侧为岸边界,右侧为开边界。开边界按正弦波给出水位过程,平均水位为0 m,振幅为3 m,周期为12 h25 min。
图6给出涨落潮各特征时刻的流速和淹没度计算结果。低潮时球冠部分露滩,高潮时浅滩完全淹没。淹没度计算结果可以较好反映出球冠及潮滩的淹没和露滩过程。
3.4 导堤算例
在实际工程中,常常会遇到导堤在高潮时淹没,而低潮时出露的情况,这种交替变化给建模带来困难。此外,由于导堤外形狭长,若采用加密网格的方法势必导致局部网格尺度极小,网格数量激增。同时,根据克朗条件,计算时间步长也需相应减小,从而导致计算时间剧增。

图5 均匀底坡上圆形浅滩地形Fig.5Topography of circular shoal on sloping bottom
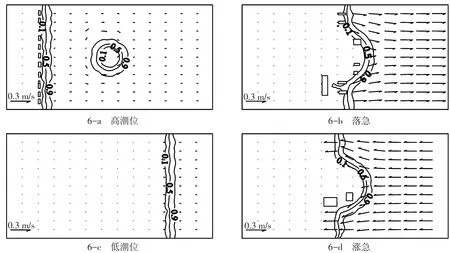
图6 圆形浅滩流速及淹没度计算结果Fig.6Computational results of velocity and submergence on sloping bottom with a circular shoal
考虑到导堤形状窄长的特点,若将导堤轴线所在位置确定为网格边线来进行网格剖分,对与导堤轴线相连的单元通过引入淹没度的方法,来反映其淹没和出露的特点,则可以避免在导堤所在位置进行过分加密的问题。
构造5000m×2500m的矩形平底水槽(图7),底部糙率为0.02,在区域中设置一顶高程为5 m的弧形堤,其轴线所在的圆弧半径为1350m,暂不考虑科氏力作用。开边界同样按正弦潮波给定。网格剖分时保证网格边线通过潜堤。
图8为涨落潮过程中各特征时刻的流速计算结果。可以看出,导堤淹没后,对流场仍有较大影响,这与实际是相符的。由于潜堤的影响,堤头处流速变大,潜堤弯曲形状的使得涨潮时堤头流速明显增大。图9为水位计算结果,图10为淹没度计算结果,可以看出,随着涨落潮的交替,导堤所在位置淹没度也随之变化。

图7 潜堤模型地形及网格剖分Fig.7Topography and meshes of the submerged dike model
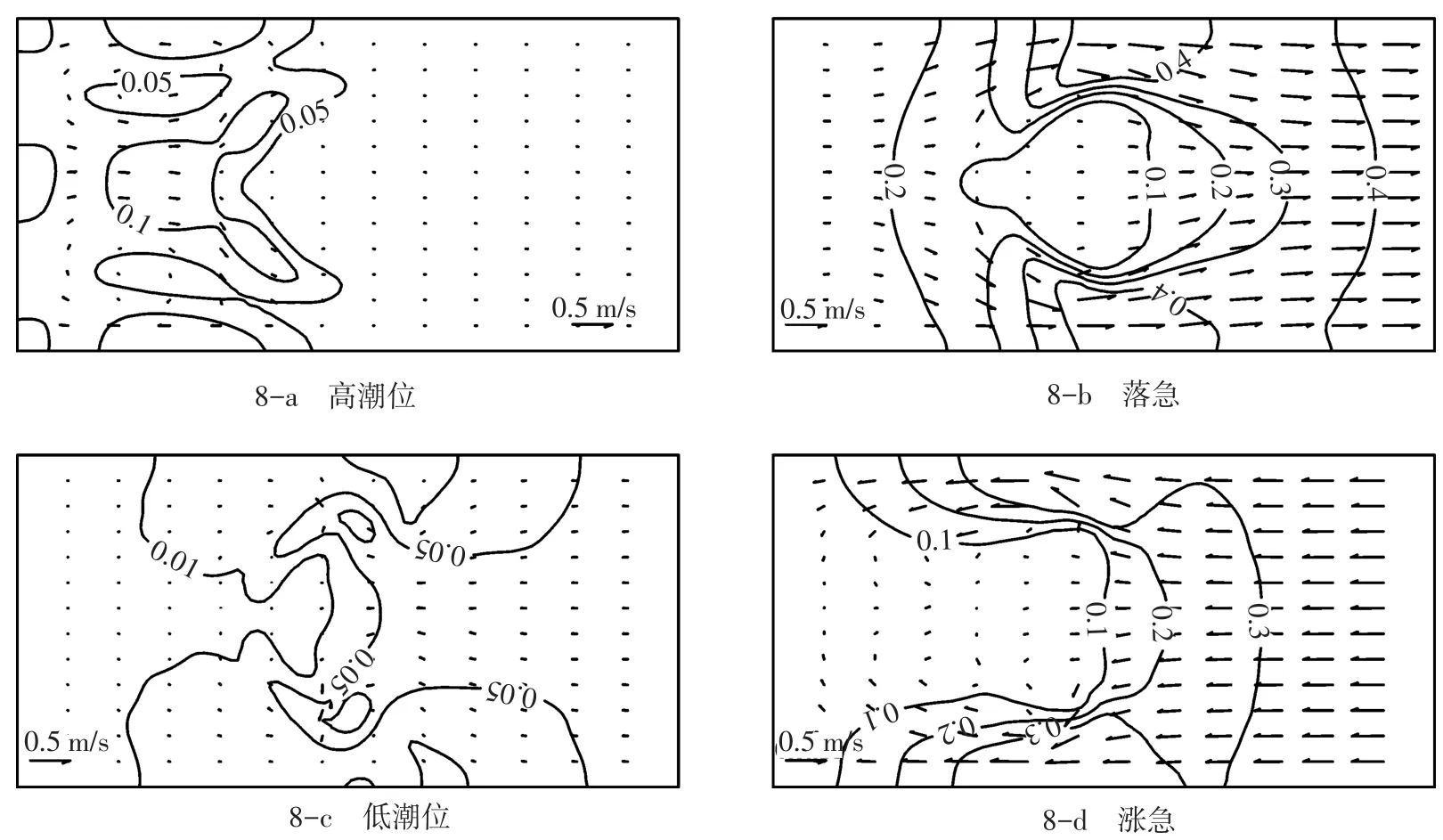
图8 流速计算结果Fig.8Computational results of velocity

图9 水位计算结果Fig.9Computational results of water surface elevation

图10 淹没度计算结果Fig.10Computational results of submergence index
4 结语
对基于有限体积法的数值通量计算方法进行了改进,导出了底坡影响下的数值通量计算格式,使得该数值模型对较大底坡的地形具有更强的适应性。提出了淹没度概念,并给出了任意网格淹没度的有限体积离散方法,使得单元可以在全干全湿两种状态下进行平滑过度,实现了水陆边界的连续性推移的过程,且计算耗时无明显增加。典型算例计算结果表明,模型在处理底坡变化剧烈的浅滩、潜堤等复杂地形时具有良好的性能。
[1]曹祖德,王运洪.水动力学泥沙数值模拟[M].天津:天津大学出版社,1994.
[2]陶建华.水波的数值模拟[M].天津:天津大学出版社,2005.
[3]谭维炎,胡四一.浅水流动计算中一阶有限体积法Osher格式的实现[J].水科学进展,1994,5(4):262-270. TAN W Y,HU S Y.Implementation of First⁃order Finite⁃volume Osher Scheme in Shallow⁃water Flow Computation[J].Advances in Water Science,1994,5(4):262-270.
[4]胡四一,谭维炎.无结构网格上二维浅水流动的数值模拟[J].水科学进展,1995,6(1):1-9. HU S Y,TAN W Y.Numerical Modelling of Two⁃Dimensional Shallow Water Flows on Unstructured Grids[J].Advances in Water Science,1995,6(1):1-9.
[5]李绍武,卢丽锋.河口准三维涌潮数学模型研究[J].水动力学研究与进展,2004,19(4):407-415. LI S W,LU L F.A Quasi⁃3D Numerical Model of Estuarine Tidal Bore[J].Journal of Hydrodynamics,2004,19(4):407-415.
[6]杨学斌.波流联合作用下二维水流泥沙数学模型研究[D].天津:天津大学,2008.
Improvements on a plane 2D numerical flow model based on FVM
LI Shao⁃wu,ZHANG Chi,YANG Xue⁃bin,LI Wen⁃shan
(State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072, China)
Precision of the numerical flux through mesh interface,treatment for dike emerging⁃submerging al⁃ternating and techniques of movable boundary have important significance for the numerical current models based on FVM.Compensational term of bottom slope in calculating numerical flux was added into the model in order to im⁃prove the interface numerical flux that was calculated by the Osher scheme.A concept of submergence index was proposed to enhance the adaptability of the model in simulation of dike emerging⁃submerging and movable bound⁃ary in the intertidal zone.A series of ideal computational examples were simulated to verify the properties of the model.Finally,satisfactory results were obtained.
numerical current model;compensation term of bottom slope;finite volume method;submerged dike;submergence index;movable boundary
TV 143;O 242.1
A
1005-8443(2014)05-0475-06
中俄将合作在俄罗斯共建大型海港
2013-10-22;
2013-12-12
国家自然科学基金(51379143)
李绍武(1962-),男,山东省人,教授,主要从事海岸动力学及海岸工程研究工作。
Biography:LI Shao⁃wu(1962-),male,professor.
据俄罗斯最大港口运营商“俄罗斯苏玛集团”在其2014年9月举行的莫斯科专场推介会上披露,俄中两国企业将合作建设年吞吐量可达到6 000万t的扎鲁比诺大型万能海港。该港位于俄远东滨海边疆区东南部,距离中国边境18 km,是俄远东地区的天然不冻港,有铁路、公路与俄内陆和中国吉林省珲春市相连。据悉,早在2014年5月举行的上海亚信峰会上,吉林省与苏玛集团签订了合作建设扎鲁比诺万能海港的框架协议。(殷缶,梅深)

