水准测量试验实例剖析

荆大威

(黑龙江省大兴安岭水文局，黑龙江加格达奇 165000)

0 引言

水准测量是测量水准点或某位置点海拔高程的一项测量工作，且应用范围也十分广泛。《水准测量规范》规定不同等级测量标准不同，但是一些指标要求苛刻。

例如三等水准测量，其中主要几项标准:仪器使用S3或其以上精度系列的水准仪。要求视距单站最大视距不得超过75 m，单站前、后视距差≤2 m，累积各站视距差≤5 m。测段总高差等等[1]。

本文就其中单站前、后视距差≤2 m，累积各站视距差≤5 m这项指标，看能否通过改正方法使成果达到与规范规定测得成果精度一样。

在实际水准测量中，如果其中某站视距差算错并随之导致相应累积视距差也出现错误值，当发现时这段必须进行返工测量。

一般来讲，发现时这一段水准测量可能已经完成，所以就产生能否不返工测量并能利用这段资料进行订正计算，使成果同样达到同等精度值，这是第一个想法[2－3]。

不按等视距进行水准测量(相对于等视距或正中水准测量就是指完全按照三等水准测量要求进行的)，即视距差或累积视距差超出三等水准测量要求范围，但是视距长度要保证≤75 m范围，这样做是为了满足估读末位数需要，或者说在测量过程中等视距就等视距测，不能等视距就不等视距测，也可称为自由式水准测量方法，这给野外测量简化了很多，方便很多。但需要增加内业计算，而使用计算机计算也很简便。

能否成为可能实现最终目标，即达到等视距水准测量精度标准，这是第二个想法[4－6]。

1 试验操作

已知某水位站的两个水准点BM4和BM2—1高程分别是178.942 m、176.161 m，两水准点距离约650 m。

用8站进行水准测量，其中每站测量3次，3次具体是这样进行的:先把水准仪放在偏中靠向后视尺的适当位置上实施前后视测量(如右图的i－1站)，测完后，接着把水准仪放到正中(等视距)位置上，进行下一轮前后视测量(如右图的i－2站)，测完后，再接着把水准仪放到偏中靠向前视尺的适当位置上继续测量(如右图的i－3站)，也就是在一站需要测3组数据，每站测完这3组数据接着进行下站3组数据测量，以此类推，直到最终完成从水准点BM4～BM2—1水准测量的全过程。

如图1所示，编号i－1、i－2、i－3分别代表第i仪器偏中靠近后视尺站所测数据对应标号、第i等视距正中仪器站所测数据对应标号、第i站偏中靠近前视尺仪器站所测数据对应标号。如i－1、i－2、i－3的i代表站，－1代表靠近后视尺位置1组，－2代表等视距位置1组，－3代表靠近前视尺位置1组。

图1 仪器布设图

2 求改正系数

2.1 公式

等视距测量这组数据不考虑，只对1－1、1－3，2－1、2－3，……，8－1、8－3进行数据处理，先分出两路线，一条是1－1，2 －1，……，8 －1;另一是1 －3，2－3，……，8－3。也就是选靠近后视尺和靠近前视尺两条线路分别计算，包括各自线路逐站计算视距差、累积视距差，视距和、累积视距和，高差、累积高差[7－8]。

如同求水准仪的视准轴与水准轴之间夹角一样，取1－1和1－3，2－1和2－3，……，8－1和8－3对应站逐级计算，根据仪器布设图，A点是后视尺位置、B 点是前视尺位置 ai－1、ai－1分别是仪器站位于i－1时两尺读数。图中两条虚线是真正的水平线，由于水准仪视准轴与水准轴之间夹角通常很小，前后视距通常可近似认为是水平距离，所以导出公式为:

式中:μi为改正系数;hi－3、hi－1为第 i站第三组和第一组的两个高差值，m;di－3、di－1为第 i站第三组和第一组的两个视距差，m;Li－3、Li－1为第 i站第三组和第一组的两个视距和，m。

改正系数计算见表1。

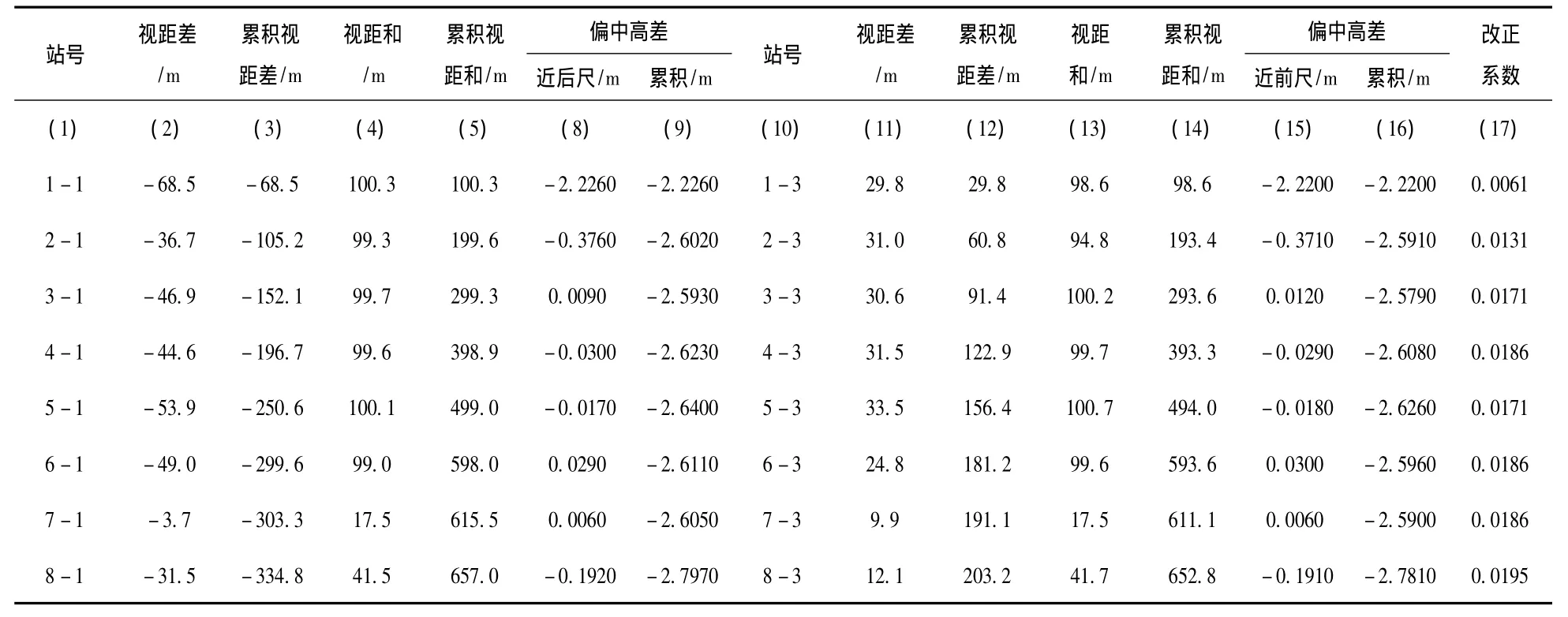
表1 改正系数计算表

2.2 求改正系数

表1中各项说明:(1)～(9)列是第一线路;而(10)～(16)列是第二线路。

这些数据是利用公式(1)、(2)、(3)由原始资料计算得到的。(17)列改正系数是利用公式(4)计算而得。

通过逐站计算改正系数发现，一站两站计算差距较大，而随着站数逐渐增加改正系数趋于稳定，也就是说改正系数是一个常数，这就为计算改正量提供可能[9－11]。

值得一提的改正系数，它是水准仪i角的一个相对表示法，只不过角度值的分母用占视距和相对值表示，即进行归一化处理而已，这一点由仪器布设图可以直观得到说明。

另外还隐含一个水平面代替水准面由于前后视距不等而带来的影响因素，但只要达到等视距就可消除影响。水准仪近或远后尺实测成果见表2。

表2 水准仪近或远后尺实测成果表

3 高差计算

3.1 线路

线路就是水准测量的路线。

当改正系数确定以后，就要把试验资料分成几种可能线路进行计算，这里分为4条线路:

1)第1线路是1－1，2－1，……，8－1，即每一水准仪站点位置都偏于后视尺。

2)第2线路是1－3，2－3，……，8－3，即每一水准仪站点位置都偏于前视尺。

3)第3线路是1－1，2－3，3－1，4－3，5－1，6－3，7－1，8－3，即一站水准仪偏于后尺而下一站偏于前尺交替进行，或者一站水准仪偏于前尺而下一站偏于后尺交替进行。

4)第4线路是选前面几个站在后面再选几个站使得终点累积视距差为0或不超出三等水准测量规范标准范围。

4条线路各自特点:

1)第一条视距差及累积视距差是负值，其累积视距差绝对值随着站数增加逐渐增大。

2)第二条视距差及累积视距差是正值，其累积视距差值随着站数增加逐渐增大。

3)第三、四线路累积视距差时大时小不确定。

4)而第四线路最终累积视距差为0或不超出三等水准测量规范标准范围。

3.2 线路计算

计算采用通过前三站算得的改正系数成果μ=0.0171，因为一台水准仪器改正系数是一个常数，不同水准仪，改正系数也不同，所以测量前要测出该仪器这一参数，为满足以后水准测量计算时需要。四条线路计算见表2，表中主要环节是计算改正值，公式为:

式中:△i为改正值，其他符号同前。

表2中各項的意义:

1)(1)、(2)项分别代表四条线路及每条线路共8站。

2)(3)～(6)和(9)、(10)项代表四条路线水准测量计算成果。

3)(12)、(13)两项是完全满足三等水准要求的此次测量成果。

4)(7)项是采用的改正系数。

5)(8)项是利用公式(5)计算值。

6)(11)项等于对应(10)项减去(8)项。

7)(14)项等于对应(11)项减去(13)的结果。3.3 与允许限差比较

包括逐站累积高差比较和总高差比较两方面(具体见表2的最后一项)，可以看出第一站第一组数据误差较大些，其余都很小。

三等水准要求不足1 km按1 km计算允许误差，即±12 mm误差限。四条线路都没有超限，所以符合三等水准标准。

根据原水准点 BM4与 BM2—1间高差－2.781 m，此 次 标 准 成 果 是 －2.783 m，相差－2 mm。

而四条线路与原高差比相差分别是 －7 mm、－5 mm、－6 mm和－1 mm，同样符合三等水准要求。

4 结论

从实际问题招手，面对野外水准测量过程中存在的一些实际条件和困难，简化野外测量工作方式，减小野外工作量，解决实际困难，这也是需要研究的课题。

尽管不同程度增加了计算量，可是有计算机的使用亦会十分方便。突破视距差的标准限制，对于转变测量方式提高测量效率也算是一个进步。该试验主要适用长距离水准测量。试验、分析、计算所得到的结果证明完全可以达到对应等级水准测量标准。

[1]中华人民共和国水利部.SL58—93水文普通测量规范[S].北京:水利电力出版社，1994.

[2]王建华，王雄，胡亚轩，梁伟锋，苏瑞，郝明.精密水准测量中的重力异常改正[J].大地测量与地球动力学，2009(02):61－64.

[3]穆子奎，刁锦通.精密水准测量中的误差[J].广东科技，2008(14):37－38.

[4]张莉，齐维君，方爱平，李明，王三明.数字水准仪误差源及检定方法初探[J].测绘通报，2005(09):59 －60，69.

[5]吕慧，张国鹏.精密水准测量中的系统误差分析[J].浙江工业大学学报，2001(04):82 －84，89.

[6]林君强.数字水准仪在二等水准测量应用的探讨[J].闽西职业技术学院学报，2010(02):122－126.

[7]马春艳，郭敏，邹友峰.数字水准仪与光学水准仪的测量精度比较[J].测绘科学，2010(01):93－94.

[8]梁菲，曹智翔.数字水准仪的一体化检测[J].科技信息，2009(33):942－943.

[9]谭诚.浅谈提高三角高程测量精度的方法[J].山西建筑，2011(07):214－215.

[10]张广伟，尚小杰.水准测量误差分析与控制[J].科技信息，2011(05):310.

[11]张振林，白怀明，张玲霞.水准测量精度影响因素及改进措施[J].山东水利，2011(05):25 －26，29.