基于地质统计学原理的会泽铅锌矿遥感线性构造解析
徐俊龙 ,温兴平 ,余 敏,李 超,王 军,张丽娟,周 杨,乔 旭
(1. 昆明理工大学国土资源工程学院,云南昆明 650093;2. 云南省矿产资源预测评价工程实验室, 云南昆明 650093;3. 西北有色地质研究院,陕西西安 710054;4. 广东省核工业地质局二九三大队,广东广州 510800)
基于地质统计学原理的会泽铅锌矿遥感线性构造解析
徐俊龙1,2,温兴平1,2,余 敏1,2,李 超3,王 军1,2,张丽娟1,2,周 杨1,2,乔 旭4
(1. 昆明理工大学国土资源工程学院,云南昆明 650093;2. 云南省矿产资源预测评价工程实验室, 云南昆明 650093;3. 西北有色地质研究院,陕西西安 710054;4. 广东省核工业地质局二九三大队,广东广州 510800)
地质统计学在自然科学领域发展迅速,凡是研究空间数据的结构性和随机性, 亦或是模拟对象的离散性、波动性等数学性质均可运用地质统计学——其理论方法在地质环境评价、石油储量计算、矿山建模及矿床地球化学等领域的研究中都取得了一系列成果。而遥感解译的复杂地质构造信息虽也符合作为地质统计学研究对象的条件, 但却鲜见其理论方法应用于遥感构造研究,从而更深入地分析地质事件及过程。本文以会泽铅锌矿为例,在通过印度IRS-P6卫星数据解译的线性构造基础上,运用了多种地质统计学方法,综合前人研究和区域地质背景,将已知的NE、NW、EW和SN 4组方位构造再划分为“成矿有利”和“非成矿有利”2组构造;在通过方差分析检验了分类的合理性后,通过因子分析和克里格插值法作出了成矿有利度图,并比对已知的的矿山厂和麒麟厂矿床,最终从构造角度为找矿工作提供了一定的参考依据。
地质统计学 遥感 线性构造 会泽铅锌矿
Xu Jun-long,Wen Xing-ping,Yu Min, Li Chao, Wang Jun, Zhang Li-juan, Zhou Yang,Qiao Xu. An analysis of linear structures in the Huize lead-zinc mine based on remote sensing images using the principle of geostatistics[J]. Geology and Exploration, 2014, 50(4):0763-0771.
地质统计学创立于20世纪60年代,在50多年的时间里已经发展成为一门相当成熟的学科并被广泛地应用——它将地球科学与统计数学相结合,运用数学的成熟理论方法研究地质理论,将定性的地学问题向定量化及自动化研究转变(尹镇南,1993;侯景儒,1996,1997)。
侯景儒等(2001)利用地质统计学探讨了固体矿产资源储量分类的若干问题;汪景宽等(2003)采用统计学相的方法研究了黑龙江海伦县中部地区六种重金属的空间变异性并取得了较好的效果;仇圣华等(2005)应用地质统计学理论建立了岩体参数变异规律的变差函数,并求出了研究区域内岩体相应的参数值;刘方成等(2005)利用地质统计学理论编制了矿床数学-经济模型软件包,并合理计算出了金宝山铂钯矿矿床矿石储量。张伟等(2008)以秘鲁D油田V层为例结合统计学理论建立了反映油田地下信息的地质三维模型;雷天赐等(2010)用地质统计学的方法对鼓锣坪Pb、Zn元素特征进行了统计分析,并得出该区Pb、Zn元素的分布与含量明显受地层及岩性控制的结论;阴江宁等(2012)利用泛克里格法对东天山Cu、Au进行了异常信息的提取和评价。
上述案例表明,地质统计学在地质环境评价、石油储量计算、矿山建模及矿床地球化学等领域应用广泛,并取得了一系列成果,但却只有少量学者在遥感构造领域应用其理论方法进行深入研究(刘建国,1985;赵不亿等,1988;王润生等,1992;郭德方等,1993;秦小光等,1993;陈建平等,1998)。事实上,随着计算机技术的发展,GIS软件已经能将从遥感图像上提取的线性构造用数字化的信息来描述,这就为利用地质统计学来分析构造的内在数学特征提供了桥梁。因此,本文将在前人研究的基础上,利用正态性检验、箱形图分析、聚类分析、方差分析等经典方法深入研究会泽铅锌矿已知的NE、NW、EW和SN 4组方位线性构造的统计特征和内在属性,并按其对成矿的作用进行再划分后通过因子分析将成矿信息降维,最终进行成矿有利度分析。
1 区域地质构造概况
云南会泽超大型铅锌矿床是川滇黔铅锌成矿区大型铅锌矿床的典型代表,在地理空间上为岩浆活动强烈的喜马拉雅构造域与太平样构造域结合部位;矿区内发育NE、NW、EW和SN 4组方位构造,其中NE向矿山厂、麒麟厂断裂和近SN向东头断裂为大型断裂构造(柳贺昌等,1999;刘淑文等,2002),铅锌矿体则产于石炭系下统摆佐组白云岩层中NE向与NW向断裂构造的交切部位(图1)。
2 遥感数据的选择及预处理
印度于2003年将IRS-P6卫星发射升空,重复周期为24天,携带有3个传感器,图像景宽141km,其中LISS3传感器具有分别位于可见光、近红外与短波红外区域的4个光谱波段,具体的波段参数见表1。
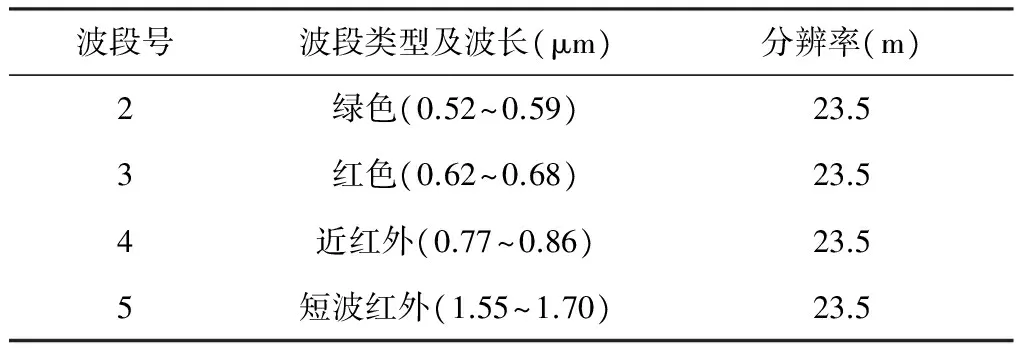
表1 LISS3波段参数
本次研究使用成像于2009年3月21日 03∶57∶14的IRS-P6 LISS3影像(SYSTEMATIC级别,条带号121,行编号52)作为基础数据,并采用OIF法(Chavezetal.,1982)选择三个最佳波段进行彩色合成。

表2 不同波段组合OIF值
从表2可知, 5、4和2三个波段组合所构成的OIF值最大,达到了28.91,且LISS3传感器的波段5是专用于地质研究的短波红外波段,故选择R:5 G:4 B:2进行假彩色合成(图2a);同时为了突出地表线性构造形迹,增强地表的纹理信息,应对波段5进行数学形态学滤波处理(图2b)。在以上图像增强工作后进行目视构造解译(图2(c))。
将构造解译图划分为r=512m的460个正方形网格区域,统计出每个正方形内线性构造的数量(ni)和累积长度(li),并将所得密度(Pi)和强度(Qi)都赋于网格内,进而分析研究区不同区段线性构造的演化特征,具体的公式如下所示:
其中,A表示单元格网的面积,实际为512 m×512 m,但为了使统计量为整数,统一将A的值取1。

图2 (a)R:5 G:4 B:2合成图像;(b)B5数学形态学滤 波图像;(c) 会泽铅锌矿线性构造解译图Fig.2 (a)image of R:5 G:4 B:2; (b) image of B5 by mathematical morphology filtering; (c) lineament inter- pretation image
3 线性构造统计分析
3.1 正态检验
按照地质统计学的观点,遥感线性构造作为地质作用的产物应具有随机性特征,而表征其特征的数学信息在二维平面空间上就应服从正态分布(赵不亿等,1988),故引入P-P图进行正态性检验。
P-P图中横坐标对应的是数据的累积概率,纵坐标对应的是数据服从正态分布时的累积概率。若数据近似服从正态分布,散点将分布在一条45°的直线周围。
图3(a)(b)中的密度和强度值点都紧密地沿着直线分布,说明线性构造在空间上服从正态分布,可认为本次线性构造的解译的结果是可信的,符合地学的一般准则,可进行后续的统计分析。
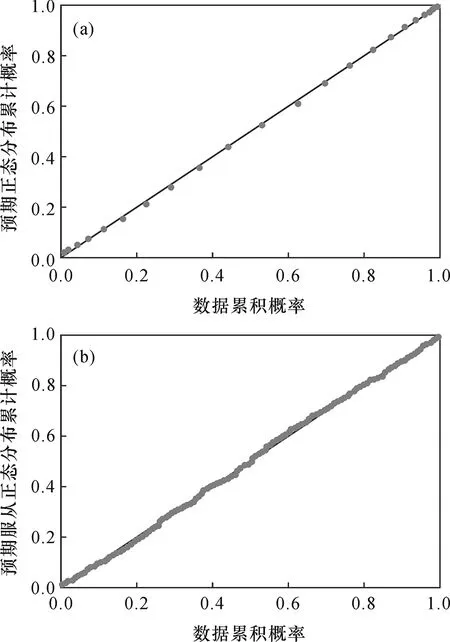
图3 (a)密度正态P-P图;(b) 强度正态P-P图Fig.3 (a)Normal P-P plot of density;(b) Normal P-P plot of strength
3.2 方位特征研究
线性构造方位特征通常用玫瑰图或散点图表示, 其目的在于了解线性构造的优势和弱势方位。因此,以0°为起始点,10°为区间,统计出相应区间内线性构造的总数及累积长度,分别作出线性构造方位-玫瑰图和方位-强度图。
图4直观反映出会泽铅锌矿断裂构造的发育特征,区域内的NE和NW向构造无论在数量上还是连通程度上都表现出明显的优势,近EW向断裂构造也较为发育,而最为劣势的方位为近SN向。
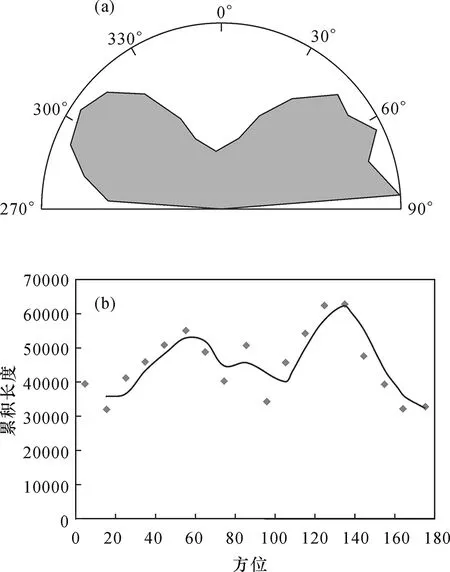
图4 (a) 线性构造方位-玫瑰图;(b) 线性构造方位-强度图Fig.4 (a) rose plot of lineament direction;(b) strength plot of lineament direction
在以上方位构造特征分析的基础上,做出NE、NW、EW和SN向构造的密度和强度箱形图,进而分析不同构造方位数据的相对位置情况和离散程度信息。
箱形图有5条竖线,盒子中从左到右分别为第一四分位数Q1、中位数Q2、第三四分位数Q3,并定义了四分位数间距IQR=Q3-Q1。在盒子左右两侧各连着一条称为须线的水平线段,表明盒子外边数据的分布;须线的端点定义为极小值Q1-1.5IQR和极大值Q3+1.5IQR,在此范围以外的值都认为是为异常值。利用箱形图可对4组方位的线性构造数据的形状进行比较。
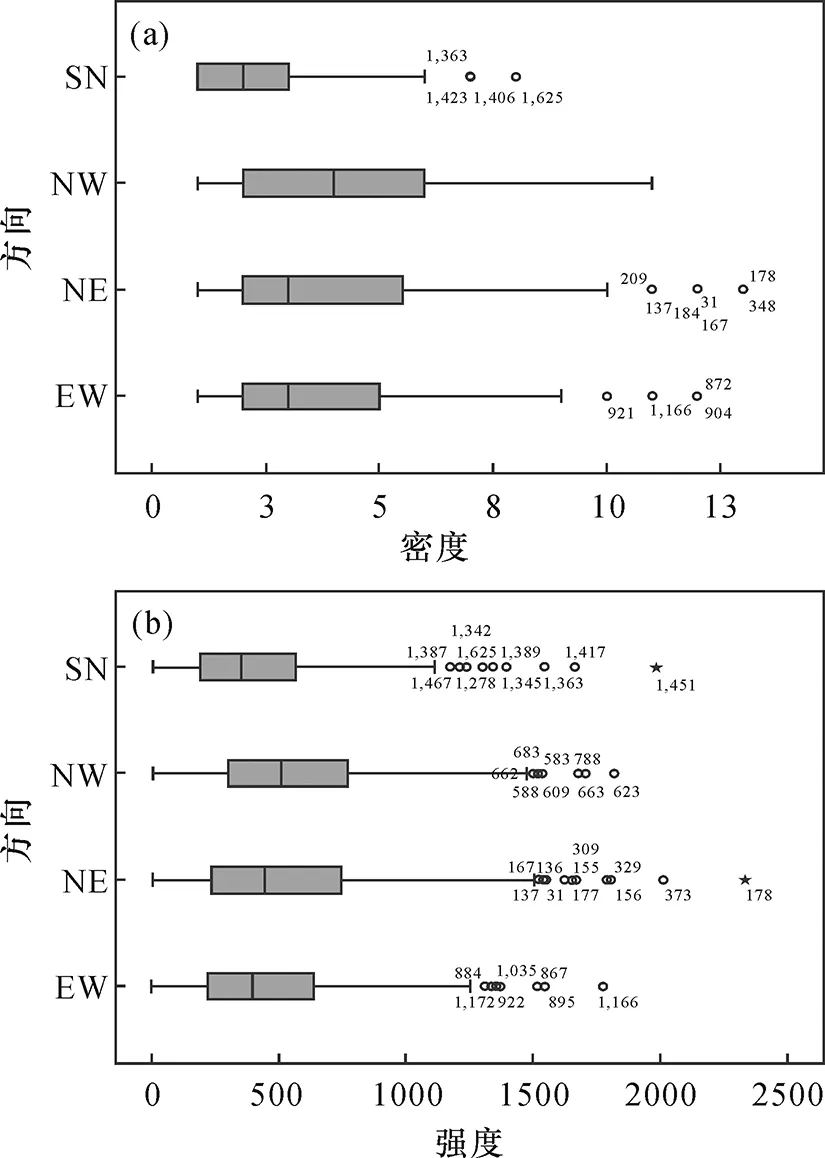
图5 (a) 密度箱形图;(b)强度箱形图Fig.5 (a) Box-plot of lineament density;(b) Box-plot of lineament strength
图5中NE和NW向的盒子最长,且须线也都较长,表明这两组方位构造在区域上离散程度最大,指示这两组方位构造有较强变异性,总体规模大于EW向和SN向,这也说明会泽铅锌矿区经历过NE和NW方向的应力集中作用,并推断这两组构造在形成后未曾再经历过高强度的其它方位的构造运动改造,未能对这2组方位的构造造成大规模改造和破坏,具有较良好的继承性;图5(a)所示NW向构造的Q1、Q2、Q3、最大值、最小值及盒子的总体长度都大于NE向构造,说明多数单元网格区域内NW向构造数量占有较大优势,而图5(b)中NE向构造强度的最大值及异常值均大于NW向,说明NE方位构造规模大、连通性强;而SN向构造无论在区域的数量上还是连通程度上都表现得最弱,并且盒子和须线的长度最短,数据离散程度小,说明SN向构造在各区域上分布平均,没有集中出现的趋势,与其它三组方位有着较明显的区别。而图5中的所有的异常值都出现在极大值Q3+1.5IQR外,却未出现小异常值,因此可推测异常值所对应的网格区域深处可能存在隐伏的断裂系,是潜在的局部构造密集发育的表现。
3.3 聚类研究及方差分析
聚类分析的基本思想是假设我们所研究的对象的样品之间存在不同程度的相似性,于是根据样本的多个指标寻找能度量其间亲疏关系的统计量,将其分为若干类。
基于以上陈述,我们将4组方位的线性构造看成是密度和强度两个变量所组成的二维空间中的4个点,然后在该空间中以点与点之间的距离来定义其相似程度,距离的度量我们采用切比雪夫距离,而聚类方法则采用组内联接法,它使得合并后的类中所有样品之间的平均距离达到最小。
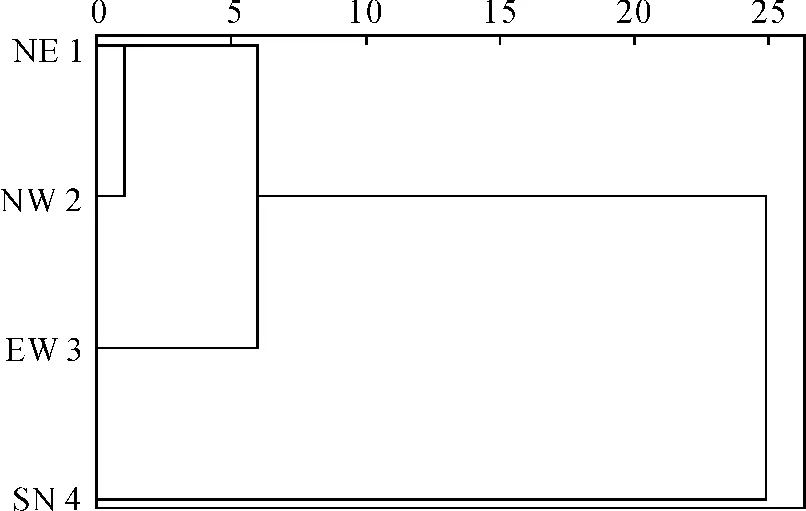
图6 聚类树形图Fig.6 The clustering tree diagram
图6中,SPSS软件默认将各类间的距离映射到0~25之间,用以表达聚类情况——当距离系数为1时,NE和NW向构造最先聚为一类;当距离系数升至6时,再与EW向聚为一类;当距离系数高升至25时,即在第3阶段4组方位的构造最终才聚成一大类。
会泽铅锌矿成矿构造的形成及应力场演化主要经历了三个时期(韩润生等,2006):主成矿期前(海西早-中期)的古构造应力方向为NE向;主成矿期(海西末期)的古构造运动方向也为NE向;而主成矿期后(印支期)则为近EW向,结合图4和图5可推测会泽铅锌区域的NE向区域大型断裂构造的形成与海西运动时期的NE向古构造应力场的作用密不可分,同时由于构造运动的共轭作用,沿大断裂沿线又发育大量密集的NW向伴生断裂与之近于垂直相交,并且造成区域海西期峨嵋山玄武岩的岩浆大范围运移,这为后期Pb、Zn元素的富集提供了一定物源和热源;地下的含矿热液沿NE向大型断裂所组成的导矿通道运移,并停留在NE与NW向断层的交切部位,最终分异结晶形成铅锌矿体;而EW向构造则是印支期近EW向以剪切为主的应力场作用的结果。构造方位有着由NE和NW方向朝着近EW方向转变的趋势,三者之间存在一定的继承性和转换关系,因此,在聚类分析的前两个阶段这3组方位构造聚为一类,这与已知的成矿构造期次具有一定的对照性;而SN断裂则按其生成的时代可划分为2类——早SN构造带推测是由SN向的基底断裂多期活动发展演化,而晚SN构造带则是滇东北区域构造演化中印支期、燕山期之后的强度最小的喜马拉雅运动造成云贵高原抬升所表现出的较弱的东西拉伸运动的产物,具有拉张性质。基于以上分析,SN向构造与NE、NW和EW向构造存在较大的差异,难以真正地视为一类,且由与其部分形成于主成矿期后,因此认为其对矿体有一定的潜在破坏作用。
NE和NW向构造在区域上具有绝对的优势(图4和图5),聚类树(图6)也将NE向和NW向构造最先聚为一类,且海西期构造运动使含矿热液沿同时期形成的这组构造运移和赋存,与成矿作用密切相关,而矿山厂和麒麟厂矿床的矿体都产于这2组构造的交切部位,因而被韩润生在内的大多数学者认可为会泽铅锌矿典型的“控矿体系”,故将其划分为一组,并定义为“成矿有利构造”;虽然近EW向构造也较为发育,且被认为是古构造应力由NE向EW转变的结果,但其主要形成于主成矿期后,和晚SN向构造一样可能对矿体造成破坏,而早SN向构造来源于成矿期前的基底构造演化,与成矿作用无关,故将这两组方位构造划为另一类,定义为“非成矿有利构造”。通过以上分析可知,会泽铅锌矿区优势方位构造与控矿构造具有内在的统一性。
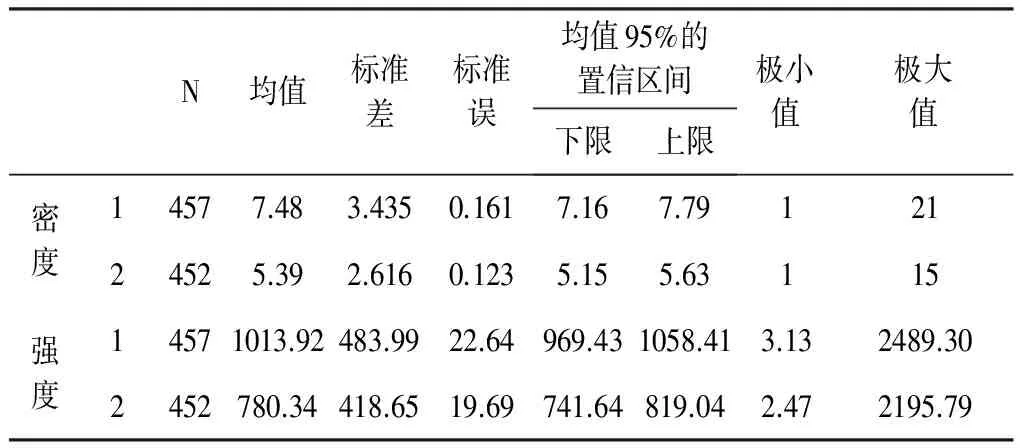
表3 描述性统计量表
注:1: 成矿有利构造;2: 非成矿有利构造。
从表3可以看出,成矿有利和非成矿有利构造在区域上的密度均值分别为7.48和5.39,总体差异不大,而标准差都小于4,总体离散程度都较小;但其强度均值差异相对明显,分别为1013.92和780.34,而规模较大的NE向构造和规模较小的NW向构造的差异是造成成矿有利构造的强度标准差值达到1058.41的原因。
以上统计结果表明,会泽铅锌矿多期次演化形成的2组构造之间存在一定的差异,然而多样性却是复杂地质系统中客观事物外在表现的基本特征,它是系统内部各种因素自身演化与外部环境影响相结合的结果,方位各异的构造也有可能来自同一根源,因而表征其特征的变量值也会有些差异,关键在于检验它们之间的差异是内在的系统差别引起的亦或是随机的偶然因素造成的,同时为了验证以上的分类结果是否可靠,应对这2组方位的构造进行相应的方差分析。
方差分析的思想认为不同水平的均数间的差别来源于系统误差SSb(自由度dfb)和随机误差SSw(自由度dfw),总偏差平方和 SSt = SSb + SSw。SSw、SSb除以各自的自由度得到其均方MSw和MSb。
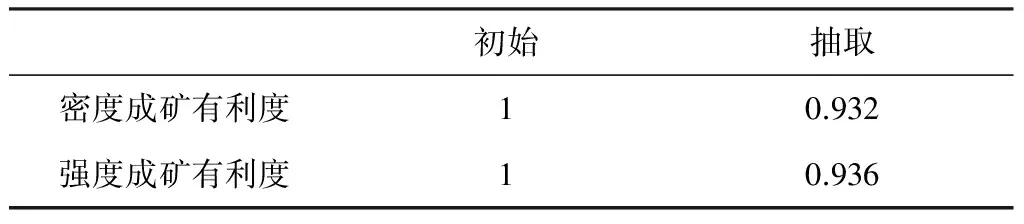
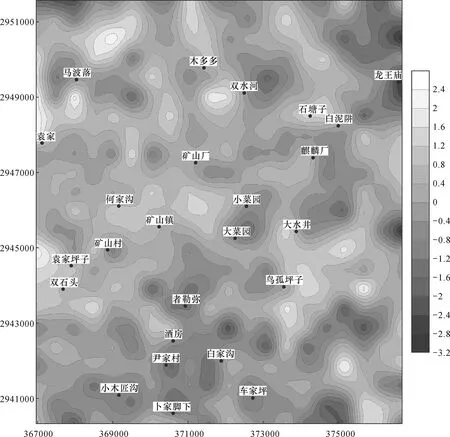
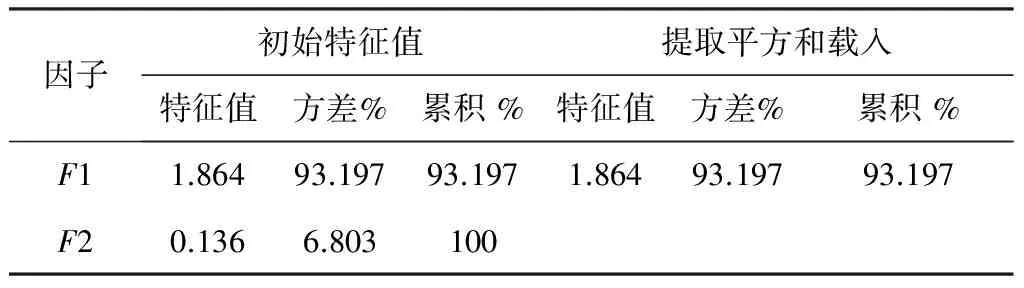
在此将2组构造的方位定义为因素的两个水平,线性构造的密度和强度作为响应变量,检验统计量F=MSb/MSw——若2组方位构造存在显著性的系统性差异,那么线性构造响应变量总的变差中由于系统影响所占的比例相对于随机变量必然较大,F值显著大于1;反之则归结于随机因素造成的,F值近似1;同理,在给定显著性水平a=0.05后,将其与F的概率P进行比较——若P 本次分析还辅助运用Bonferroni法来检验方差的一致性。 表4 方差一致性检验表 从表4可以看出,P密度和P强度分别为0.000和0.005,都明显小于所设置的显著性水平0.05,因此可认为2组构造在密度和强度两个变量的方差都不存在一致性,数据离散程度差异大。 表5显示2组线性构造密度的组间平方和为994.56,组内平方和为8467.29,相应的检验统计量F为106.53,对应的概率P为0;而强度的组间平方和为12398543.25,组内平方和为185868422.50,相应的检验统计量F为60.50,对应的概率P依旧为0——而我们设置的a=0.05,明显大于P,结合表3和表4的结果,拒绝原假设,认为2组方位的构造差异显著,并且这种差异是系统性原因而非偶然因素造成的,对成矿的作用性也不同。 表5 方差分析 综上所述可知,这2组构造同处于滇东北同一构造演化体系之中,因而具有一定的联系和相似性;然而通过多种统计学的方法最终找出了它们的内在的系统差异,因此可认为构造分类的结果严谨可靠。 3.4 因子分析 因子分析的核心思想是降维,建立尽可能少的互不相关的新变量,而且这些新变量在反映信息方面尽可能不造成损失。 首先将成矿有利构造的频数(累积长度)占线性构造频数总和(长度总和)的比值定义为密度成矿有利度(强度成矿有利度),其值在0到1之间。 表6 相关系数表 表6数据显示,线性构造的密度成矿有利度和强度成矿有利度两个变量之间存在很强的相关性,相关系数r=0.864,可以认为这两个变量带有大量重叠的信息,应进行因子分析。 表7 共同度表 表7说明因子分析后新变量抽取了原始“密度成矿有利度”93.2%和“强度成矿有利度”93.6%的信息。 表8中特征值的大小反映了公共因子的方差贡献率,抽取平方和载入栏为根据特征值大于1的原则提取的因子的特征值、方差百分数及累积值,F1解释的方差占总方差的93.197%,已基本全面地反映了所有信息。 图7 成矿有利度图Fig.7 Ore-forming favorableness 表8 总方差解释表 以上过程已经将2个变量转变为1个因子F1,而后计算出每个正方形区域的F1因子得分,利用克里格插值法作出成矿有利度图。 图7中F1的值反映的是成矿有利度的正信息,区间由原先的0~1转变为-3.2~2.4,其值越低表示其受EW和SN向构造的影响越大,对成矿无指示意义;相反,值越高则表示区域受占优势NE和NW控矿构造的影响越大,构造交切的可能性越大,因此中高值区域可视为潜在的矿化点,研究区的成矿有利度值总体在0以上;矿山厂矿床和麒麟厂矿床的产出则受NE向导矿构造和作为配矿构造的NW向断裂构造的控制异常明显——矿山厂矿床和麒麟厂矿床一带成矿有利度值明显较高,达到了0.4以上,可以此为参照,将高值区域划分为找矿的重点区域。 (1) 在RS和GIS技术的有力支持下,将通过遥感图像解译的线性构造用密度和强度两个数学参数来表达,即将定性描述的构造信息转化为定量信息,这为利用地质统计学理论来研究和解决构造问题提供了桥梁;在此基础上,遥感线性构造的密度和强度数据通过了P-P图的正态性检验,这为后续统计分析工作提供了保障。 (2) 方位-玫瑰图与方位-强度图中反映出的NE和NW向构造最为发育的特征,与研究区内地质构造条件基本吻合;其次,利用箱形图分析4组不同方位构造数据相对位置情况和离散程度信息,得出NE和NW方向构造在区域上离散程度最大且具有较强变异性的结论;在此基础上,结合聚类分析的结果和研究区构造体系的生成发展史,从“构造控矿”的观点出发,将各项数学特征最为相近的NE、NW向断裂组合定义为“成矿有利构造” ,而将EW、SN向断裂组合定义为 “非成矿有利构造”;最后,利用方差分析探明了这2组构造差异的显著性程度和根源,为构造划分的可靠性提供了定量依据。 (3) 通过因子分析将2类构造成矿信息为唯一的反映成矿有利度正信息的因子F1;在F1图中,已知的矿山厂矿床和麒麟厂矿床所在区域的值达到了0.4以上,以此为参考,为找矿工作提供指导方向。 (4) 本文将地质统计学方法与遥感构造研究进行了有机的结合,在加工和浓缩构造数学信息的基础上,利用经典的统计方法和直观的统计图表深入分析和比对了NE、NW、EW和SN构造内在特征的差异,在构造研究中具有一定的创新性和实际意义。 Chavez P S,Berlin G L,Sowers L B.1982.Statistical method for selecting Landsat MSS ratios[J].Journal of Applied Photographic Engineering,8(1):22-30 Chen Jian-ping ,Xu Jin.1998.Remote sensing statistics of indirected dsiplay on surface caused by buried geological anomaly[J].Earth Science—Journal of China University of Geosciences,23(2):129-132(in Chinese) Qiu Sheng-hua,Yang Lin-de,Chen Gang.2005.Application of geostatistics in determining rock mass parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 24(9):1545-1548(in Chinese) Guo De-fang,Xie Qing-yun,Lan Yu-qi,Bao Shao-hua,Zhang Yong-ping,Li Xiao-meng.1993.Linear syspem field analysis[J]. Remote Sensing for Land&Resources (4):8-16(in Chinese) Han Run-sheng,Chen Jin,Huang Zhi-long,Ma De-yun,Xue Chuan-dong,Li Yuan,Zou Hai-jun,Li Bo,Hu Yu-zhao,Ma Geng-sheng,Huang De-yong,Wang Xue-kun.2006. Dynamics of tectonic ore-forming processes and localization-prognosis of concealed orebodies—As exemplified by the Huize super-large Zn-Pb-(Ag-Ge)District,Yunnan[M].Beijing: Science Press:135-158(in Chinese) Hou Jing-ru.1996. Present situation of geostatistical development and discussion on some problems[J]. Gold Geology ,2(1):1-11(in Chinese) Hou Jing-ru.1996. Review and prospect of geostatistics (spatial-information statistics) development in China[J].Geology and Prospecting, 33(1):53-58 (in Chinese) Hou Jing-ru,Huang Jing-xian.2001. Application of geostatistics in classification for resources/rrserves of solid fuels and mineral commodities[J].Geology and Prospecting,37(6):61-66(in Chinese) Lei Tian-ci,Huang Gui-cheng,Lei Yi-jun,Hu Jun-liang.2010. Application of geostatistics on spatial distribution of Cu,Pb,Zn in Guluoping[J].Journal of Guilin University of Technology,30(4):501-506(in Chinese) Liu Fang-cheng,Qin De-xian,Yan Yong-feng,Li Bao-zhu,Qin Lai-yong,Hong Tuo.2005.Geostatistics and its application in Jingbaoshan Pt-Pd deposit,Yunnan[J].Geology and Resources, 14(4):293-296(in Chinese) Liu He-chang,Lin Wen-da.1999.Regularity research of Ag,Zn,Pb ore deposits north-east Yunnan Province[M].Yunnan:Yunnan University Press:60-66(in Chinese) Liu Jian-guo.1985. Lineament density central symmetry statistical analysis and its application for geological study in ancient volcanic Terrain[J]. Earth Science-Journal of Wuhan College of Geology,10(4):119-130(in Chinese) Liu Shao-ping,Tang Jun,Xu Xiao-hong.2011.The methods and application on mathematical geology[M].Beijing:Petroleum Industry Press:57-128(in Chinese) Liu Shu-wen,Wei Kuan-yi,Xu La-ping.2002.The thrust nappe tectonics system and the metallogenic prediction of the Pb-Zn deposit in Huize,Yunnan[J]. Northwestern Geology,35(3):84-89(in Chinese) Qin Xiao-guang,Zhao Bu-yi,Li Fu-an.1993.Quantitative analysis fpr circular structures based on the remote sensing images[J].Remote Sensing for Land&Resources,(2):54-60(in Chinese) Wang Jing-kuan,Zhao Yong-cun,Zhang Xu-dong,Wang Qiu-bing.2003. Studies on the spatial variability of heavy metal contents in black soils in central areas of Hailun[J]. Chinese Journal of Soil Science34(5):398-403(in Chinese) Wang Run-sheng,Yang Wen-li.1992. Digital analysis of lineament field in remotely sensed image[J]. Remote Sensing for Land&Resources, (3):49-54(in Chinese) Yang Zheng-xi,Wu Qian-hong,Peng Zhi-xing,Yan Bing.2008. Geological data analysis tutorial[M].Beijing:Science Press:30-112(in Chinese) Yin Jiang-ning,Xiao Ke-yan,Zou Wei,Wang Zhong,Lu Lu.2012. Applying geostatistics to extract geochemical information in East Tianshan[J]. Journal of Jilin University(Earth Science Edition) ,42(3):887-894(in Chinese) Yin Zhen-nan.1993. The situation of geostatistical application in China and at abroad[J].Geology and Prospecting,29(8):37-39(in Chinese) Zhang Wei,Lin Cheng-yan,Dong Chun-mei.2008. Application of multiple—point geostatistics in geological modeling of D Oilfield in Peru[J].Journal of China University of Petroleum (Edition of Natural Science) ,32(4):24-28(in Chinese) Zhao Bu-yi,Qin Xiao-guang.1988.the Quantitative analysis method of remote sensing structure[J]. Geological Science and Technology Information,7(1):127-136(in Chinese) [附中文参考文献] 陈建平,徐 进.1998.隐伏地质异常地表间接显示模拟的遥感地质统计分析[J].地球科学—中国地质大学学报,23(2):129-132 仇圣华,杨林德,陈 岗.2005.地质统计学理论在岩体参数求解中的应用[J].岩石力学与工程学报,24(9):1545-1548 郭德方,谢青云,兰玉琦,包绍华,张永平,李小孟.1993.线性体场分析[J].国土资源遥感,(4):8-16 韩润生,陈 进,黄智龙,马德云,薛传东,李 元,邹海俊,李 勃,胡煜昭,马更生,黄德镛,王学琨.2006.构造成矿动力学及隐伏矿定位顶测——以云南会泽超大型铅锌(银、锗)矿床为例[M].北京:科学出版社:135-158 侯景儒.1996.地质统计学发展现状及对若干问题的讨论[J].黄金地质,2(1):1-11 侯景儒.1997.中国地质统计学(空间信息统计学)发展的回顾及前景[J].地质与勘探,33(1):53-58 侯景儒,黄竞先.2001.地质统计学在固体矿产资源/储量分类中的应用[J].地质与勘探,37(6):61-66 雷天赐,黄圭成,雷义均,胡俊良.2010.地质统计学在湖南省鼓锣坪Cu、Pb、Zn元素空间分布格局研究中的应用[J].桂林工学院学报,30(4):501-506 刘方成,秦德先,燕永锋,李保珠,秦来勇,洪 托.2005.地质统计学及其在云南金宝山铂钯矿的应用[J].地质与资源,14(4):293-296 柳贺昌,林文达.1999.滇东北铅锌银矿床规律研究[M].云南:云南大学出版社:60-106 刘建国.1985.影像线性体密度一中心对称度综合分析方法及其在古火山岩区地质研究中的应用[J].地球科学-武汉地质学院学报,10(4):119-130 刘绍平,汤 军,许晓宏.2011.数学地质学方法及应用[M].北京:石油工业出版社:57-128 刘淑文,魏宽义,许拉平.2002.云南会泽铅锌矿田控矿构造体系及成矿预测[J].西北地质,35(3):84-89 秦小光,赵不亿,李甫安.1993.环形构造成矿预测定量分析—以桂西北地区金矿预测为侧[J].国土资源遥感,(2):54-60 汪景宽,赵永存,张旭东,王秋兵.2003.海伦县土壤重金属含量的空间变异性研究[J].土壤通报,34(5):398-403 王润生,杨文立.1992.遥感线性体场的数量化分析[J].国土资源遥感,(3):49-54 阳正熙,吴堑虹,彭直兴,严 冰.2008.地学数据分析教程[M].北京:科学出版社:30-112 阴江宁,肖克炎,邹 伟,王 中,路 璐.2012.地质统计学在东天山化探信息提取中的应用[J].吉林大学学报(地球科学版),42(3):887-894 尹镇南.1993.地质统计学在国内外应用现状[J].地质与勘探,29(8):37-39 张 伟,林承焰,董春梅.2008.多点地质统计学在秘鲁D油田地质建模中的应用[J].中国石油大学学报(自然科学版),32(4):24-28 赵不亿,秦小光.1988.遥感构造的定量分析方法[J].地质科技情报,7(1):127-136 An Analysis of Linear Structures in the Huize Lead-Zinc Mine Based on RemoteSensing Images Using the Principle of Geostatistics XU Jun-long1,2, WEN Xing-ping1,2, YU Min1,2, LI Chao3, WANG Jun1,2, ZHANG Li-juan1,2, ZHOU Yang1,2,QIAO Xu4 (1.FacultyofLandResourceEngineering,KunmingUniversityofScienceandTechnology,Kunming,Yunnan650093;2.MineralResourcesPredictionandEvaluationEngineeringLaboratoryofYunanProvince,Kunming,Yunnan650093;3.NorthwestNonferrousGeologyInstitute,Shaannxi710054;4.NuclearIndustryGeologicalBureau293BrigadeinGuangdongProvince,Guangzhou,Guangdong510800) Geostatististics have developed rapidly in the field of natural science. The theory and method of geological statistics can be applied to study spatial data structure and randomness or to model discrete volatility and other mathematical properties, and a series of achievements have been made, especially in the field of geological environment evaluation, oil reserves estimation, mine modeling and ore deposit geochemistry. The remote sensing interpretation of complex geological structure information can meet the requirements of geological statistics, but few of its theory research methods have been applied to studies of structures based on remote sensing images. This paper takes the Huize lead-zinc mine as an example, and uses a variety of geological statistics methods through India IRS-P6 satellite data interpretation to divide the known NE, NW, EW and SN-trending structures into 2 groups of ore-forming favorableness and non-ore-forming favorableness structures based on previous studies and regional geological background. We test this classification rationality through variance analysis, and make an ore-forming favorability map through principal component analysis and Kriging interpolation method. This study also compares the results with the known mines and the kylin factory deposit, and provides a scientific basis for ore prospecting work from the point of view of structure. geostatistics,remote sensing,lineament,Huize lead-zinc deposit 2013-11-18; 2014-02-26;[责任编辑]郝情情。 国家自然科学基金联合基金(U1133602)、国家自然科学基金(41101343)和昆明理工大学成矿动力学与隐伏矿预测创新团队(2008)联合资助。 徐俊龙(1988年-),男,昆明理工大学国土资源工程学院硕士研究生,现主要从事遥感地质及矿产资源调查评价工作。E-mail:871566374@qq.com。 温兴平(1970年-),男,昆明理工大学国土资源工程学院教授,博士,现主要从事地球化学与遥感地质研究工作。 E-mail:wfxyp2008@gmail.com。 P627 A 0495-5331(2014)04-0763-9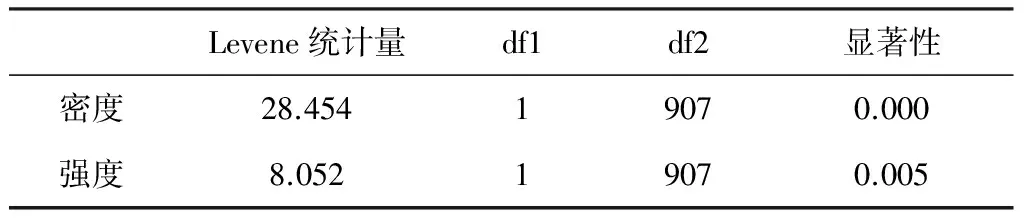
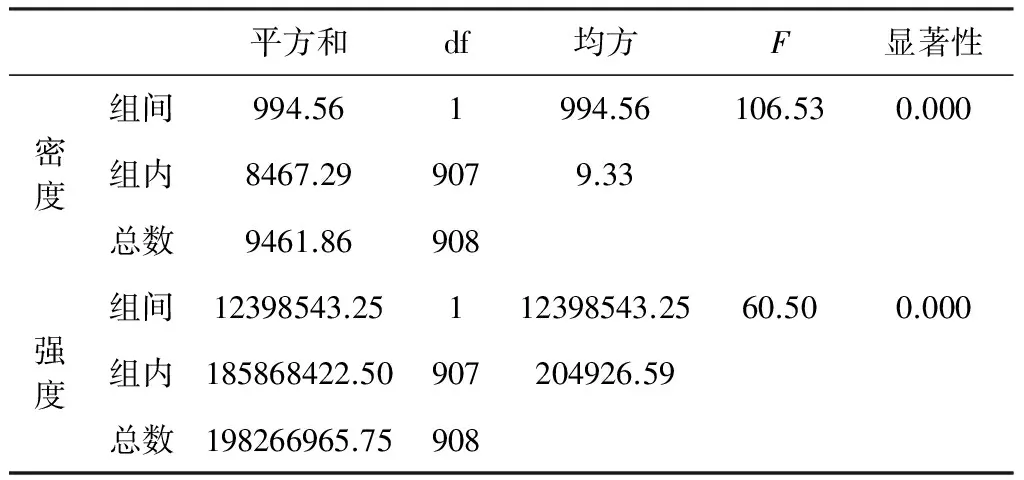

4 结语

