TI地层声学各向异性随钻评价方法的数值研究
王瑞甲,乔文孝,车小花,鞠晓东
(1.中国石油大学油气资源与探测国家重点实验室,北京 102249; 2.中国石油大学北京市地球探测与信息技术重点实验室,北京 102249)
TI地层声学各向异性随钻评价方法的数值研究
王瑞甲1,2,乔文孝1,2,车小花1,2,鞠晓东1,2
(1.中国石油大学油气资源与探测国家重点实验室,北京 102249; 2.中国石油大学北京市地球探测与信息技术重点实验室,北京 102249)
采用三维有限差分方法模拟偶极子声源在含钻铤的各向异性地层井孔中激发的声场,研究地层各向异性对偶极模式波频散特征的影响,并提出从随钻四分量偶极子声波数据中提取地层快、慢横波慢度及其各向异性的方法。结果表明,偶极子声源在各种地层井孔中均可激发对横波慢度的方位各向异性敏感的偶极模式波:对于快速地层, F2模式的低频部分对地层横波慢度及其方位各向异性最为敏感;对于中速和慢速地层,弯曲波较高频率部分对地层横波慢度较为敏感。采用各向同性地层建模的方法可以较为准确地提取地层的快、慢横波慢度,提取结果的误差小于4%。
随钻测井;声波测井;各向异性;偶极子
随钻声波测井是一种发展迅速,应用广泛的声学测量技术[1-4]。在横波测量中,人们选用了四极子声源进行测量[1]。但是,限于四极子声源的辐射指向性,难以利用其获得地层横波的各向异性信息。由于随钻四极子声波测井仪换能器的安装方式与正交偶极子声波测井仪相同,且其接收站具备正交偶极子接收功能,通过合理的电路设计,可以较为方便地实现正交偶极子声波测井,所以随钻正交偶极子测井是进行地层各向异性评价首选方法。关于偶极子声源在各向异性地层中激发的声场的研究大部分集中在电缆测井条件下的各向异性地层井孔中的声场特征方面,主要包括3种情况:VTI地层竖直井[5-9]、TI地层斜井和水平井[10-14]和正交各向异性地层井孔[15]。有关随钻条件下偶极子声源在各向异性地层中激发的声场的研究相对较少。Sinha 等[16]研究了多极子声源在含钻铤各向异性地层斜井中激发的声场,认为偶极模式波可以用于提取过井轴的两个正交的平面内的剪切模量。王瑞甲等[17-18]采用三维有限差分方法研究了正交偶极子声源在含钻铤TI地层斜井中激发的声场,证实了随钻条件下偶极子声源对于地层各向异性的方位敏感性。笔者重点研究地层各向异性的存在对于偶极模式波频散特征的影响以及从四分量偶极子数据中提取快、慢横波慢度的算法。
1 模拟方法
三维有限差分方法是进行声场模拟的常用数值方法。在直角坐标系下,采用应力和速度表示的运动方程和本构方程[6]分别为

式中,vx、vy、vz分别为x、y、z方向上的速度分量;τxx、τyy、τzz分别为x、y、z方向上的正应力;τxy、τyx、τxz为剪切应力;ρ为介质的密度;gab(a、b=x~z)应表示力变化速度的体积源,与体力源fi(i=x~z)组合使用可以模拟各种声源;C为介质的弹性常数矩阵。网格划分方式采用中心差分格式的交错网格实现,声学模型边界采用完全匹配层(PML)技术。由于计算模型较大,采用基于OpenMP和MPI的混合编程技术实现算法的并行。所采用的有限差分算法的具体实现方法见文献[17]。
本文中所关注的地层类型为横向各向同性(TI)地层,其中地层的TI旋转对称轴与井轴(z轴)垂直。这种地层可采用5个独立的弹性参数描述,
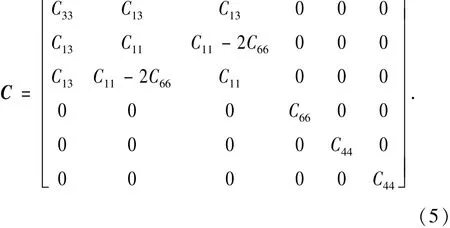
将各向异性地层看作是各向同性地层的微扰,把矩阵C分解为表征参考的各向同性介质的矩阵CISO和表征扰动的矩阵C′,即

对于偶极子声源而言,不同偏振方向的声源激发的模式波不同,所以选取的参考各向同性地层的参数不同。对于HTI地层(井轴与TI旋转对称轴垂直),选取两套各向同性地层参数,分别对应不同偏振方向的偶极子声源。对与SH波偏振方向一致的偶极子声源而言,参考的各向同性地层的纵波速度选择为,横波速度选择为对与SV波偏振方向一致的偶极子声源,对应的各向同性地层的纵、横波速度分别选择为和通过对比偶极子声源在各向异性地层与对应的各向同性地层井孔内激发的波形以及模式波的频散曲线,分析地层各向异性的存在(C′)对于模式波的影响,并进一步讨论采用各向同性地层建模从弯曲波中提取快、慢横波慢度的方法的可行性。
2 数值模拟结果及分析
2.1 数值模型
图1为含钻铤各向异性地层井孔声学模型示意图。该模型为典型的柱状径向分层介质模型,模型从内到外依次为水层、钢(钻铤)、水层和地层,其外径分别为0.054、0.18、0.24 m和无穷大。模型主计算区域大小为1 m×1 m×4.8 m,x、y和z方向的空间采样步长分别为0.005、0.005和0.0125 m。井轴与坐标轴z平行。地层为横向各向同性介质,其介质对称轴为S,平行于坐标轴x,与井轴垂直。定义偶极子声源的偏振方向同y坐标轴的夹角为β。特别地,当β=0°时,偶极子源偏振方向同地层快横波(SH波)偏振方向一致;当β=90°时,偶极子源偏振方向同地层慢横波(SV波)偏振方向一致。声源加载在距离底界面0.8 m处,采用在钻铤外径处加载两个振动相位相反的点声源的方法模拟偶极子声源。偶极子接收器同样置于钻铤外径处,源距范围为2.0~3.5 m,接收器间距为0.15 m。由于本文中重点研究地层模式波,不涉及隔声及钻铤波问题的研究,为压制钻铤波的幅度,在发射器到源距最小的接收器之间将钻铤截断。
为了分析不同地层情况下偶极子声源激发的弯曲波的频散特性,选取快速、中速、慢速3种地层进行模拟。快速地层采用Cotton Vally Shale的弹性参数[10],慢速地层采用Austin Chalk的弹性参数[10],中速地层采用实验室内用酚醛树脂材料制作的模型的TI弹性参数测量值[17]。数值模拟中采用的各种地层的弹性参数见表1。模拟时采用的钻铤材质的纵、横波速度分别为5.860和3.130 km/s,密度为7.860×103kg/m3;钻铤内外流体的纵波速度为1.500 km/s,密度为1.000×103kg/m3。
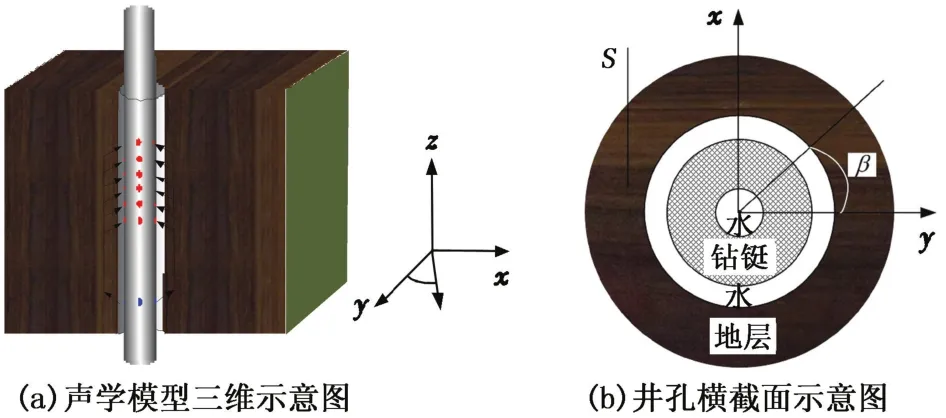
图1 含钻铤各向异性地层井孔声学模型示意图Fig.1 Schematic diagram of acoustic model for logging while drilling in a HTI formation
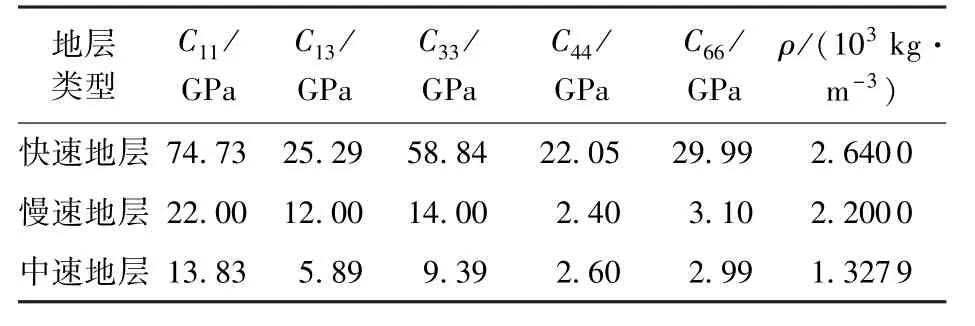
表1 地层参数Table 1 Formation parameters
2.2 快速地层
快速地层情况下,偶极子声源激发的声场的模拟结果如图2所示,其中(a)、(b)为β=0°的偶极子声源激发的波形及频散分析结果,(c)、(d)为β= 90°的偶极子声源激发的波形及频散分析结果。频散分析方法采用了文献[19]中介绍的方法。图中,实线表示各向异性地层的计算结果,虚线为各向同性地层结果,“SH”和“SV”标注的短线分别表示地层SH波和SV波的慢度,“S”标注表示横波,“F”标注表示依赖地层传播的偶极子模式波,“C”标注表示依赖钻铤传播的偶极子模式波。在频率慢度相关图中,未标注的相关条带均为噪声信号。
从图2(a)可见,在各向异性和各向同性地层情况下,偶极子波形的形态基本一致:波形初至部分几乎完全重合;对于后续波部分,各向同性地层情况下的波形到时略早于各向异性地层情况。在图2(c) 中,两种地层情况下的偶极子波形几乎完全重合。上述计算结果表明,地层各向异性的存在对于快速地层井孔内激发的偶极子声场的影响较小。
进一步通过频散分析结果研究地层各向异性对模式波频散曲线的影响。从图2(b)和(d)可观察到两种偶极模式波,分别标记为F1和F2。文献[2, 18,20]的研究结果表明,这两种偶极子波为最低阶的液浸无限大钻铤中的偶极模式波和无钻铤充液井孔中最低阶偶极模式波耦合而成的两种新的模式波。文献[18]通过灵敏度分析的方法对此现象进行了研究,认为两种模式波在低频和高频部分的影响因素不同。对于F1模式,其低频部分的频散特性由钻铤控制,高频部分主要受地层参数影响;对于F2模式,其低频部分由地层参数控制,高频部分由钻铤参数控制。从图2(b)可见,对于F1的低频部分(3 kHz以下)和F2的高频部分(4 kHz以上),各向异性地层和各向同性地层情况下的频散曲线基本重合,这说明地层各向异性的存在对其影响较小;而对于F1的高频部分(4 kHz以上)和F2的低频部分(4 kHz以下),地层各向异性的存在对模式波的频散规律则有一定的影响。图2(d)也有类似的现象。结合文献[18]的研究结果,本文中认为该现象是由于模式波在低频段和高频段的影响因素不同造成的:依赖于钻铤传播的部分(F1的低频部分和F2的高频部分)受地层参数影响很小,从而受地层各向异性影响也很小;而依赖地层传播的部分(F1的高频部分和F2的低频部分),则受地层各向异性的影响相对较大。
另外,从图2(b)和(d)可见,对于不同方向的偶极子声源和不同的地层,F2低频部分的慢度均趋近于对应的地层体横波慢度,这说明对于快速地层可以通过F2模式的低频部分获得快、慢横波的慢度。图2(b)中,在2~4 kHz频率范围内,地层各向异性的存在使得F2模式的频散曲线向低频有较大偏移,这使得图2(a)中两种地层情况下的偶极子波形存在差异;图2(d)中,在该频率范围内,地层各向异性的存在使得F2模式的频散曲线也向低频偏移,但由于偏移值较小,在图2(c)中不能够明显观察到。
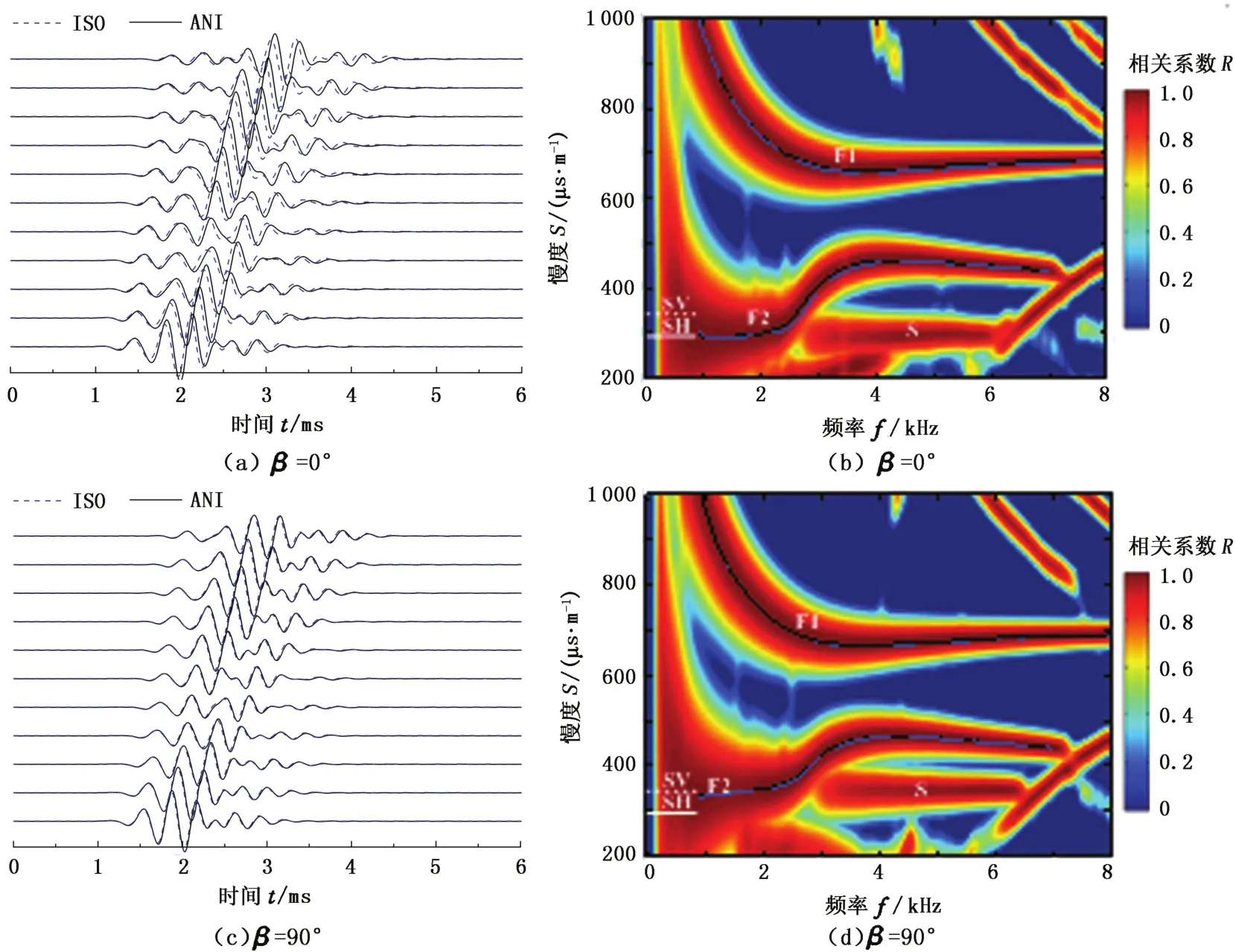
图2 偶极子声源在含钻铤快速地层井孔中激发的波形及频散分析结果Fig.2 Waveforms and dispersion analysis results in fluid-filled borehole with a collar surrounded by fast formations excited by dipole sources
2.3 中速地层
图3是中速地层情况下的数值模拟结果,其中(a)、(b)采用的声源为β=0°的偶极子声源,(c)、(d)为β=90°的偶极子声源。由图3(a)和(c)可见,各向异性地层情况下的弯曲波与对应的各向同性地层情况下的弯曲波的形态基本一致,到时比各向同性地层略晚,且在β=0°时,两种地层情况下波形的到时差别较大,在β=90°时,差别较小。这说明,对于该地层模型,各向异性的存在使得弯曲波传播速度略降低,且对于β=0°的偶极子声源而言更为明显。从图3(b)和(d)可见,在低频段(0~1.2 kHz),基本观察不到地层各向异性的存在对于弯曲波频散特性的影响,而在高频段(1.5~7 kHz),地层各向异性的存在使得弯曲波的慢度增加。这是因为低频部分的弯曲波主要由钻铤参数控制,而高频部分则主要受地层参数的影响。在利用弯曲波反演地层横波慢度时,应选择对地层参数敏感的频率段。对于该地层而言,选择1.5 kHz以上的频率是合适的。另外,与快速地层的计算结果相比,在图3(b)和(d)中观察到了地层六极子波(Hexpole mode),但未观察到其与地层各向异性相关的信息。
2.4 慢速地层
图4为慢速地层井孔中偶极子声源激发的声场。从图4(a)和(c)可见,对于慢速地层的情况,各向异性地层和对应的各向同性地层井孔情况下的弯曲波的形态基本一致,到时略有差别。地层各向异性的存在使得β=0°时弯曲波的到时滞后,而β= 90°时弯曲波的到时提前。从图4(b)和(d)可见,在低频段,各向异性地层和各向同性地层两种情况下的弯曲波频散曲线基本重合,但随着频率增加,二者出现差异,并越来越大。对于β=0°的情况,地层各向异性的存在使得弯曲波慢度增加;对于β=90°的情况,地层各向异性的存在使得弯曲波的慢度降低。如果采用各向同性地层建模,通过频散校正的方法来计算快、慢横波的慢度,对于β=0°的情况,反演得到的快横波慢度会大于真实快横波慢度;而对于β=90°的情况,反演得到的慢横波慢度会小于真实的慢横波慢度。反演结果的误差与计算采用的频率有关,对于该地层而言,频率越高,误差越大。选择恰当的频率可以降低反演结果的误差。

图3 偶极子声源在含钻铤中速地层井孔中激发的波形及频散分析结果Fig.3 Waveforms and dispersion analysis results in fluid-filled borehole with a collar surrounded by intermediate speed formations excited by dipole sources
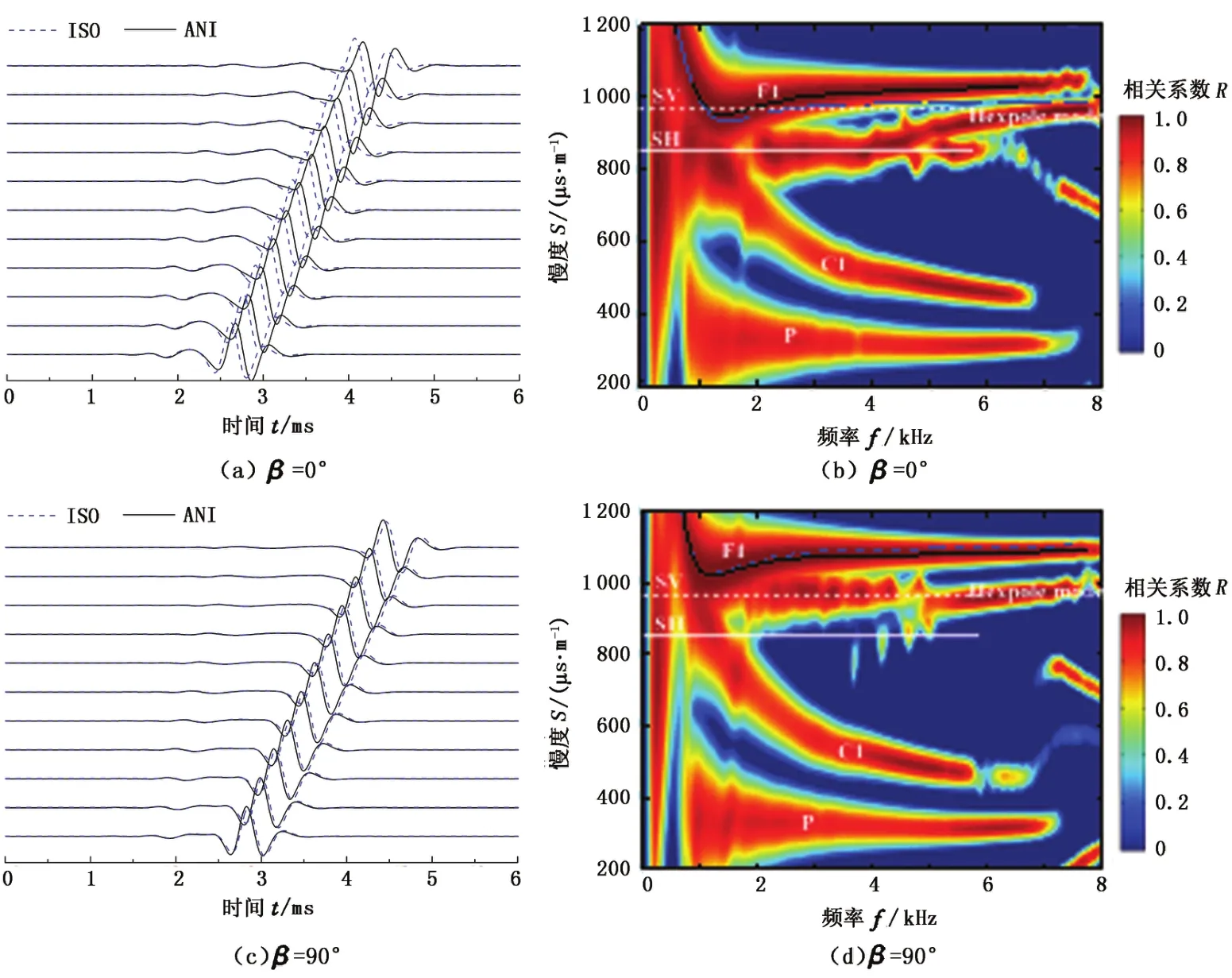
图4 偶极子声源在含钻铤慢速地层井孔中激发的波形及频散分析结果Fig.4 Waveforms and dispersion analysis results in fluid-filled borehole with a collar surrounded by slow formations excited by dipole sources
3 各向异性提取方法及数值验证
3.1 随钻情况下的地层各向异性提取方法
在随钻测量条件下,由于井孔中钻铤的存在,传统的基于时域的各向异性提取方法不适用于地层各向异性参数的提取。本文中提出基于正演模型的随钻各向异性提取方法。为简化反演过程的复杂度,以各向异性地层快、慢横波各自对应的各向同性地层建立随钻测井声学模型。在各向同性地层井孔中,弯曲波的慢度取决于地层的密度和纵、横波慢度、钻铤的密度和纵、横波慢度以及钻铤内外流体的密度及纵横波慢度,计算公式为

式中,ω为圆频率;α为该频率下弯曲波的慢度;
分别为地层的密度及纵、横波慢度;ρcol、和SScol分别为钻铤的密度及纵、横波慢度;ρf和分别为钻铤内外流体的密度及纵横波慢度;r0、r1和r2分别为钻铤内、外半径和井孔半径。由于实际的钻铤是固定的,钻铤密度ρcol、钻铤纵波慢度钻铤横波慢度钻铤内外半径r0和r1及井孔半径r2均可以看作已知量。另外,钻铤内外流体的密度及慢度ρf和可以根据实际情况确定。其他参数,包括地层的密度ρform可以根据密度测井资料确定,地层的纵波慢度可以根据单极子纵波的测量结果确定。据此,可得到弯曲波的慢度与地层横波慢度的关系:

特别地,对于快横波,选择为快横波慢度,对于慢横波,选择为慢横波慢度,其计算公式分别为

对于测得的四分量偶极子波形,首先通过Alford四分量偶极子波形旋转方法获取快、慢波波形,然后通过波场分离的方法获得较为纯净的地层偶极子波。快、慢横波慢度提取的目标函数为
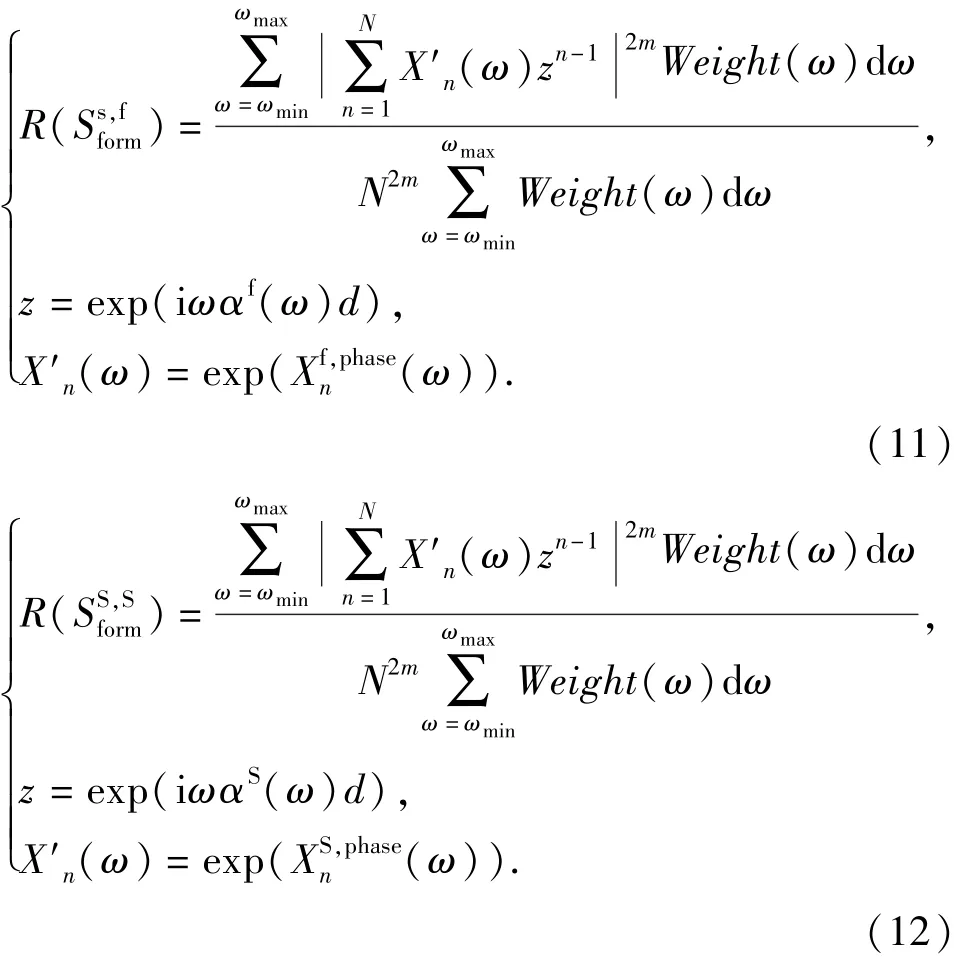
式中,(ω)和(ω)分别为快、慢地层偶极子波波形的相位谱;d为接收器源距;m为乘因子;Weight(ω)为加权系数;ωmin和ωmax分别为计算的最低频率和最高频率。有关加权系数的构造方法见文献[21]。使得目标函数R()和R()取得极大值的和即为所求的快、慢横波慢度。横波慢度的各向异性值可以近似地采用下式确定:
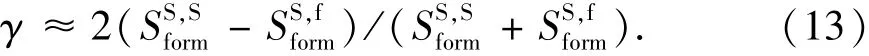
综上所述,从随钻正交偶极子资料中提取地层各向异性的算法可以分为以下几步:
(1)理论计算不同情况下含钻铤井孔中偶极子波的频散曲线,并将数据存储于硬盘中。
(2)通过Alford四分量偶极子波形旋转的方法和波场分离的方法获得快、慢偶极子波波形。
(3)从硬盘中读取偶极子波的频散曲线,并采用插值的方法对频散曲线进行重构,然后采用式(11)~(13),获取地层的快、慢横波慢度和各向异性值,并确定快横波方位角。
3.2 模拟数据的处理结果
图5为快速地层井孔中模拟的偶极子波形数据的处理结果,其中图5(a)为不同横波慢度所对应的偶极模式波(F2)频散曲线,图5(b)为根据式(11)、(12)计算得到的目标函数。图5(a)中的偶极子波的频散曲线对应图2中的F2模式。从图5(a)可见, F2模式在低频段对于横波慢度变化最敏感,随频率增加,敏感性降低。另外,随着横波慢度增加,F2模式的频散曲线向低频偏移。由此可知,对于快速地层,选择低频部分的数据可以提高反演结果的可靠性。对于该地层模型,采用1~2.5 kHz的频率范围是合适的。
从图5(b)可见,目标函数极大值所对应的值,即计算得到的快、慢横波的慢度值分别为301.1和346.9 μs/m,地层真实的快、慢横波慢度分别为296.7和346.0 μs/m,反演得到的快、慢横波慢度误差分别为1.5%和0.26%。提取的横波慢度的各向异性值为14.1%,小于真实的各向异性值15.3%。结合图2可知,该误差是由于在反演过程中采用了各向同性地层建模而引入的。
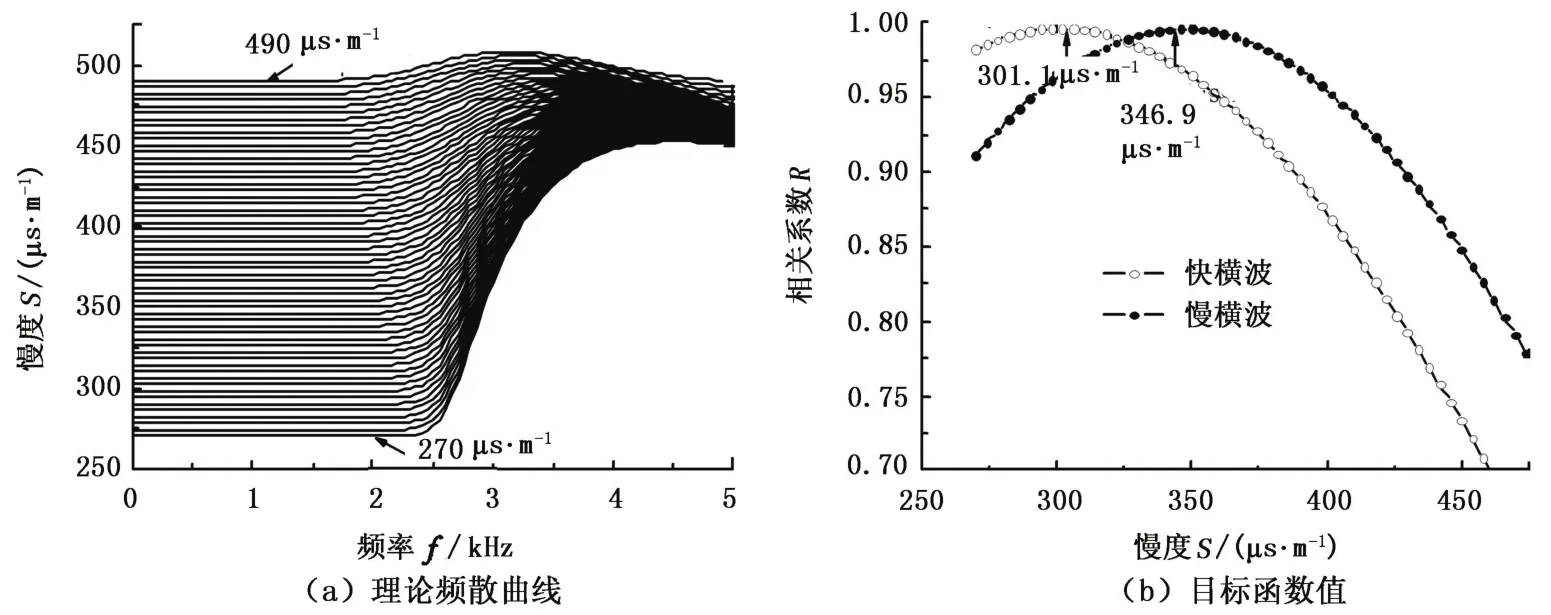
图5 快速地层模型处理结果Fig.5 Results of fast formation model
同样,采用该方法处理了中速地层偶极子声波波形数据,如图6所示。从图6(a)可见,弯曲波在低频段对地层横波慢度变化不敏感,在稍高的频率段对地层横波慢度敏感。结合图3中的频散分析结果,选取理论的弯曲波频散曲线极小值所对应的频率点作为计算的下限频率ωmin,计算的频带宽度为1 kHz。由于不同横波慢度下,理论频散曲线极小值所对应的频率是变化的,所以计算目标函数所选用的频率范围也是变化的。从图6(b)可见,反演得到的快、慢横波的慢度分别为688.4和733.1 μs/m。地层真实的快、慢横波慢度分别为666.4和714.7 μs/m。反演结果的误差分别为3.3%和2.6%。提取的横波慢度的各向异性值为6.3%,略小于真实的各向异性值7.0%。
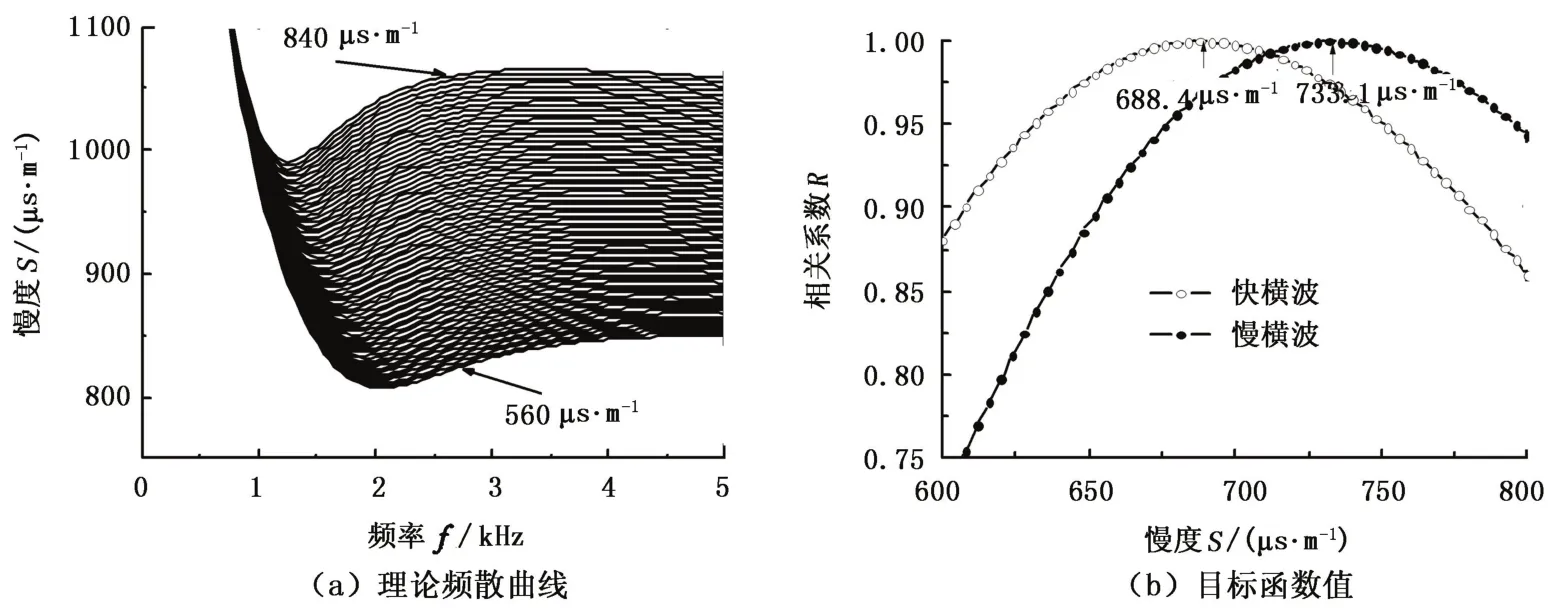
图6 中速地层模型处理结果Fig.6 Results of intermediate speed formation model
图7为慢速地层井孔偶极子数据的处理结果。由图4可见,频率越高,各向异性地层和各向同性地层情况下的弯曲波频散曲线差别越大。为了尽量减小地层的各向异性对计算结果的影响,与中速地层一致,选取理论弯曲波频散曲线极小值所对应的频率点作为计算的下限频率ωmin,计算的频带宽度为1 kHz。从图7(b)可知,反演得到的快、慢横波的慢度分别为873.2和954.8 μs/m,地层真实的快、慢横波的慢度分别为842.4和957.4 μs/m,误差分别为3.7%和0.27%。该结果与图4中的频散分析结果一致。另外,提取的横波慢度的各向异性值为8.9%,真实的各向异性值为12.8%。地层各向异性的存在使得快弯曲波慢度增加,慢弯曲波慢度减小,采用各向同性地层建模的方法提取的各向异性值与真实值有一定差别。
从上述处理结果可以看出,从模拟数据中反演得到的慢横波的误差小于快横波的误差,这是由于本文中研究的3种地层各向异性的存在对慢弯曲波频散特性的影响大于其对快弯曲波的影响。这也可以在图2~4的频散图中观察到。综上所述,采用各向同性地层建模计算地层快、慢横波慢度,误差小于4%,说明该方法是可行的。
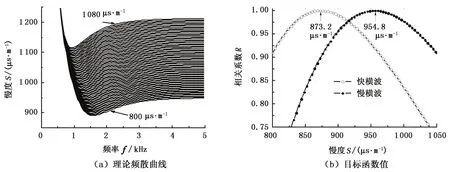
图7 慢速地层模型处理结果Fig.7 Results of slow formation model
4 结果讨论
正演模型中输入参数的误差可能导致反演得到的快、慢横波慢度和各向异性值出现较大的误差,结合随钻单极子和四极子的测量结果进行联合反演可以在很大程度上保证计算结果的可靠性。
在随钻测井中,另外一个很重要的问题是实时的数据处理和传输。四分量偶极子波形数据量较大,目前的遥测技术无法实现波形数据的实时传输,各向异性提取程序需要在井下进行,从而限制了算法的计算复杂度。由图5~7可以看出,在一定的频率段内,弯曲波慢度随地层慢度的变化呈线性。因此,可通过近似公式计算地层各向异性值

式中,ΔSS为快、慢横波的慢度差;ΔSflex为快、慢弯曲波的慢度差;为主频附近弯曲波慢度相对于地层横波慢度的灵敏度。ΔSflex可以通过时域内的弯曲波慢度计算或者快、慢波匹配等方法得到。则可以通过理论计算得到,并存储于井下存储器中。进一步采用式(13)可近似得到地层横波慢度的各向异性值。
本文中未涉及钻井液循环及钻进过程中的噪声、仪器的偏心和钻铤波等对测量结果的影响。这些因素可能对测量结果有较大的影响。针对这些问题,需要在仪器设计及信号处理方面做进一步的研究。
5 结 论
(1)在随钻条件下,偶极子声源在各种地层井孔中均可激发对横波慢度的方位各向异性敏感的偶极模式波。对于快速地层,F2模式的低频部分对地层横波慢度及其方位各向异性最为敏感;对于中速和慢速地层,弯曲波的高频部分对对地层横波慢度较为敏感。
(2)偶极子声源在各向异性地层和对应的各向同性地层井孔中激发的偶极子波形,形态相同,慢度略有差别。
(3)采用各向同性地层建模的方法可以较为准确地提取地层的快、慢横波慢度,提取结果的误差小于4%。
[1] TANG X M,CHENG C H.Quantitative borehole acoustic methods[M].San Diego:Elsevier Science Publishing Co Inc,2004.
[2] SINHA B K,SIMSEK E,ASVADUROV S.Influence of a pipe tool on borehole modes[J].Geophysics,2009,74 (3):E111-E123.
[3] 王华,陶果,王兵,等.多极子随钻声波测井波场模拟与采集模式分析[J].地球物理学报,2009,52(9): 2402-2409.
WANG Hua,TAO Guo,WANG Bing,et al.Wave field simulation and data acquisition scheme analysis for LWD acoustic tool[J].Chinese Journal Geophysics,2009,52 (9):2402-2409.
[4] 陈雪莲,魏周拓.随钻单极子声反射测井数值模拟[J].石油学报,2012,33(5):835-840.
CHEN Xuelian,WEI Zhoutuo.Numerical simulation of monopole acoustic reflection imaging logging in the logging-while-drilling condition[J].Acta Petrolei Sinica, 2012,33(5):835-840.
[5] SCHMITT D P.Acoustic multipole logging in transversely isotropic poroelastic formations[J].JASA,1989,86 (6):2397-2421.
[6] 张海澜,王秀明,张碧星.井孔中的声场与波[M].北京:科学出版社,2004.
[7] 陈雪莲,王瑞甲.径向分层TI孔隙介质井孔中激发的模式波的数值研究[J].地球物理学报,2008,51(4): 1270-1277.
CHEN Xuelian,WANG Ruijia.A numerical study on the mode waves excited by multipole sources in the fluidfilled borehole in radially layered transversely isotropic porous medium[J].Chinese Journal Geophysics,2008, 51(4):1270-1277.
[8] 陈雪莲,王瑞甲.横向各向同性弹性地层井孔中模式波的探测深度[J].吉林大学学报:地球科学版,2008, 38(3):502-507.
CHEN Xuelian,WANG Ruijia.Investigating depth of mode waves in the borehole surrounded by transversely isotropic elastic formation[J].Journal of Jilin University (Earth Science Edition),2008,38(3):502-507.
[9] HE X,HU H S.Borehole flexural modes in anisotropic formations:the low-frequency asymptotic velocity[J]. Geophysics,2009,74(4):E149-E158.
[10] SINHA B K.Elastic-wave propagation in deviated wells in anisotropic formations[J].Geophysics,2006,71 (6):D191-D202.
[11] HE X,HU H S,GUAN W,Fast and slow flexural waves in a deviated borehole in a homogeneous or layered anisotropic formation[J].Geophys J Int,2010, 181(1):417-426.
[12] 闫守国,宋若龙,吕伟国,等.横向各向同性地层斜井中正交偶极子激发的声场的数值模拟[J].地球物理学报,2011,54(9):2412-2418.
YAN Shouguo,SONG Ruolong,LÜ Weiguo,et al.Numerical simulation of acoustic field excited by cross-dipole source in deviated wells in transversely isotropic formation[J].Chinese Journal Geophysics,2011,54 (9):2412-2418.
[13] 王瑞甲,乔文孝,车小花,等.TI地层井孔中正交偶极子声波测井的物理模拟[J].中国石油大学学报:自然科学版,2012,36(6):62-69.
WANG Ruijia,QIAO Wenxiao,CHE Xiaohua,et al. Physical simulation of cross-dipole acoustic logging in borehole surrounded by TI formation[J].Journal of China University of Petroleum(Edition of Natural Science), 2012,36(6):62-69.
[14] 王瑞甲,乔文孝,鞠晓东,等.不同偏振方向的偶极子声源在HTI地层井孔中激发声场的实验研究[J].地球物理学报,2013,56(2):707-717.
WANG Ruijia,QIAO Wenxiao,JU Xiaodong,et al. Experimental study of the acoustic field in the borehole surrounded by HTI formations excited by dipole sources with different orientations[J].Chinese Journal Geophysics,2013,56(2):707-717.
[15] CHENG N Y.Borehole wave propagation in isotropic and anisotropic media:three-dimensional finite difference approach[D].Cambridge:Department of Earth, Atmospheric,and Planetary Sciences,MIT,1994.
[16] SINHA B K,SIMSEK E.Sonic logging in deviated wellbores in the presence of a drill collar:2010 SEG Annual Meeting,Expanded Abstracts,Denver US,October 17-22,2010[C].US Tulsa:SEG,c2010.
[17] 王瑞甲,乔文孝,鞠晓东.利用随钻正交偶极子声波测井评价地层各向异性的数值研究[J].地球物理学报,2012,55(11):3870-3882.
WANG Ruijia,QIAO Wenxiao,JU Xiaodong.Numerical study of formation anisotropy evaluation using cross dipole acoustic LWD[J].Chinese Journal Geophysics, 2012,55(11):3870-3882.
[18] 王瑞甲.各向异性地层声波测井模拟研究[D].北京:中国石油大学地球物理与信息工程学院,2012.
WANG Ruijia.Simulation research on acoustic logging in fluid-filled borehole surrounded by anisotropic formations[D].Beijing:College of Geophysics and Information Engineering in China University of Petroleum, 2012.
[19] 王瑞甲,乔文孝,鞠晓东.一种多通道声波测井信号频散分析方法[J].测井技术,2012,36(2):135-140.
WANG Ruijia,QIAO Wenxiao,JU Xiaodong.A multichannel acoustic logging signal dispersion analysis method[J].Well Logging Technology,2012,36(2):135-140.
[20] 崔志文.多孔介质声学模型与多极源声电效应测井和多极随钻声测井的理论与数值研究[D].长春:吉林大学物理学院,2004.
CUI Zhiwen.Theoretical and numerical study of modified Biot's models,acousto-electric well logging and acoustic logging while drilling excited by multipole acoustic sources[D].Changchun:College of Physics,Jilin University,2004.
[21] WANG R J,QIAO W X,CHE X H.A new method of extracting shear slowness from borehole mode waves: CISP'10:proceedings of the 2010 3nd International Congress on Image and Signal Processing,Yantai,China, October 16-18,2010[C].US Piscataway:IEEE, c2010.
(编辑 修荣荣)
Numerical study of anisotropy evaluation method by acoustic logging while drilling in TI formations
WANG Ruijia1,2,QIAO Wenxiao1,2,CHE Xiaohua1,2,JU Xiaodong1,2
(1.State Key Laboratory of Petroleum Resources and Prospecting in China University of Petroleum,Beijing 102249,China; 2.Key Laboratory of Earth Prospecting and Information Technology in China University of Petroleum,Beijing 102249,China)
The acoustic field excited by dipole sources in a fluid-filled borehole with a collar surrounded by anisotropic and the corresponding isotropic formations was simulated by a three-dimension finite difference method.The effects of formation anisotropy on dispersions of borehole modes were investigated.The results show that the dipole source can excite dipole modes which are sensitive to the formation anisotropy in all types of formations.For fast formation,the low-frequency part of F2 mode is most sensitive to shear velocities and anisotropy of the formation,while for intermediate speed and slow formations,the higher frequency part is more sensitive to shear velocities.A method of extracting formation fast and slow shear slowness and anisotropy parameters from four-component dipole waveforms is proposed,and is verified using numerical data. The error of extracted result is less than 4%.
logging while drilling;acoustic logging;anisotropy;dipole source
P 631.8
A
1673-5005(2014)04-0065-09
10.3969/j.issn.1673-5005.2014.04.009
2013-06-05
国家自然科学基金项目(11204380,11374371,11134011,61102102);国家油气重大科技专项(2011ZX05020-009);中国石油科技创新基金(2013D-5006-0304);中国石油天然气集团公司项目(2011A-3903,2011B-4001)
王瑞甲(1986-),男,博士,主要从事地球物理测井方法、检测声学等方面的研究。E-mail:wruijia@foxmail.com。
乔文孝(1956-),男,教授,博士,博士生导师,研究方向为声波测井、检测声学。E-mail:qiaowx@cup.edu.cn。
王瑞甲,乔文孝,车小花,等.TI地层声学各向异性随钻评价方法的数值研究[J].中国石油大学学报:自然科学版,2014,38(4):65-73.
WANG Ruijia,QIAO Wenxiao,CHE Xiaohua,et al.Numerical study of anisotropy evaluation method by acoustic logging while drilling in TI formations[J].Journal of China University of Petroleum(Edition of Natural Science),2014,38(4):65-73.

