舰艇护航编队防空队形配置方法研究*
姜鲁东 孙建华 余家祥
(1.海军装备部 北京 100071)(2.海军大连舰艇学院舰炮系 大连 116018)
舰艇护航编队防空队形配置方法研究*
姜鲁东1孙建华2余家祥2
(1.海军装备部 北京 100071)(2.海军大连舰艇学院舰炮系 大连 116018)
针对舰艇护航编队防空需要,从定量分析的角度,研究并给出了水面舰艇护航防空队形配置方法。该方法将舰炮视为编队防空的主要武器,以优化警戒幕半径为目标,构建了编队防空队形配置模型。以典型舰艇和舰炮性能为输入参数,通过算例验证了队形配置模型的有效性。
舰艇; 编队; 队形配置
Class Number O212.8
1 引言
水面舰艇护航编队的主要任务护送和掩护我海上作业的运输舰船及海洋调查、科学实验船只,其主要目的是保障被护航舰船的安全[1]。编队执行护航任务时,对空防御是的一项重要工作[2~3]。为了提高防御的效果,护航编队通常要组成防空队形,以应对来自于任意方向的空袭。
目前,关于水面编队防空的研究主要集中在武器-目标分配方向[4]。关于编队防空队形配置的研究成果较少[5],多数研究以定性分析为主,难以客观地反映防空队形的作战效果。针对上述问题,本文在分析水面舰艇护航编队防空队形的关键问题的基础上,从定量的角度给出了防空队形配置方法。
2 问题的提出
一般情况下,护航编队防空队形配置为警戒幕队形,即被护航舰船居中,警戒舰艇呈环形等间隔配置在被警戒舰船的周围,如图1所示。

图1 常见的警戒幕队形
采用图1所示队形的优点是[6]:对于任一方向的来袭目标,均可由与其航路相邻的两舰对其抗击。当目标接近到火炮有效射程时,警戒舰开始开火,当目标飞临编队中心时,炸弹已落水,即可停火。
显然,警戒幕半径Rx大小不同,抗击敌人的效果是要发生变化的。如果Rx太小,各警戒舰只能迎击目标,而打尾追的时间太短,防御效果不是最佳的;相反,如果Rx太大,由于舰炮射程有限,两警戒舰的火力交叉范围太小,火力太稀疏,防御效果也不是最优的,因此寻求最优的Rx是配置防空队形的关键。
接下来将以定量分析为基础,计算在舰炮抗击条件下的最优Rx值,使得来袭敌机被毁伤概率最大。
3 数学模型
驱护舰具有防空能力的舰炮一般有主炮和副炮两种,因此来袭敌机被毁伤概率Ps可以表示为
Ps=1-(1-P2)(1-P1)
(1)
式(1)中,P1为副炮对来袭敌空中目标的毁伤概率,P2为主炮对来袭敌空中目标的毁伤概率。
假设一发主炮炮弹对飞机的毁伤概率为P2/1,一发副炮炮弹对飞机的毁伤概率为P1/1,则
P1/1=1-(1-P1/1)n1
(2)
P2/1=1-(1-P2/1)n2
(3)
式(2)中,n1为敌方飞机到达被警戒舰前与其邻两舰副炮发射的弹数;式(3)中,n2为敌方飞机到达被警戒舰前与其邻两舰主炮发射的弹数。
再假设副炮、主炮的实际射速为m1发/分、m2发/分,则有
n1=2×A1×t1×m1/60
(4)
n2=2×B2×t2×m2/60
(5)
式(4)和式(5)中,2表示相邻两舰的火力叠加;t1、t2分别为副炮、主炮的平均射击时间(s);A1、B2为某型舰的任意方向平均可使用的副炮、主炮门数,由于目标进入方向是任意的,而且舰船可以转机动,所以此值等于各炮射界之各除以360[7]。
现在问题的关键是算出t1、t2。由于两者算法相同,所以本文以t1为例说明t1和t2的计算过程。
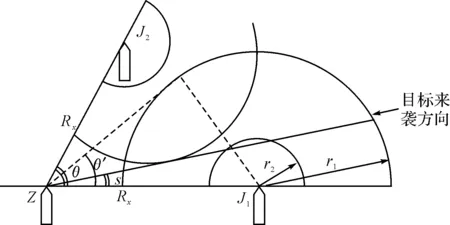
1) 当Rx 图2 警戒幕半径Rx小于火炮拦截距离r1的态势 图2中,Z为被警戒舰,J1、J2为相邻两警戒舰,θ为两舰之间的夹角(显然,θ=360/N,N为警戒舰数),r1为副炮拦截距离在海平面的投影,rs为死区在海平面的投影。 这样,目标在射界内的航程为 (6) 式(6)中,rCPA为航路与警戒舰J1的距离,且有 rCPA=Rxsin(s) (7) 2rS1为航路在死区内的距离,且有 (8) 在此航路上,副炮的射击时间t11为 (9) 式(9)中,V为目标速度(m/s),td1为炮弹飞行时间修正量且有 td1=tf(r1,H)-tf(Rx,H) (10) 式(10)中,tf(x,y)是按基本射表确定的炮弹飞行时间函数且x、y分别为目标水平距离和高度。 由于目标从各个方向进入的概率相等,因而有 (11) 2) 当Rx≥r1时(如图3所示) 图3中,各参数的定义如下: θ′=sin-1(r1/Rx) (12) 目标在射界内的航程为 (13) 这样,当td1=0时,有: (14) (15) 图3 警戒幕半径Rx大于火炮拦截距离r1的态势 用同样的方法可以算得t2。 有了t1和t2,可以根据舰炮射击效率评定原理[6]计算目标被毁伤概率PS。 设定编队由同属舰型Ⅰ的数艘舰艇组成,与该型相对应的A1=2.33、B2=0.75,主、副炮单发命中概率分别取0.0025和0.001,且该型舰的主、副炮拦截距离及射击死区数据如表1所示。 表1 主、副炮拦截距离及死区参数 按上面的数模及数据,根据不同的目标高度H、舰种、舰数进行计算,得出PS随Rx和H的变化曲线如图4和图5。图4和图5分别为3艘、4艘某舰组成警戒幕的情况。三条曲线由上而下分别表示高度为100m、1000m、2000m三种情况。纵坐标表示目标被毁伤概率PS值,横坐标表示警戒幕半径Rx值。由图可知,高度为100m、1000m、2000m时的PS值的最大值所对应Rx值分别为10~12链、8~11链、7~9链。 为了更好地说明模型的合理性,另取舰型Ⅱ和舰Ⅲ重复上述计算,并将舰型Ⅰ、舰型Ⅱ和舰型Ⅲ对不同高度的目标的运算结果列入表2~表4中。 图4 三艘某型舰编队PS随Rx和H的变化曲线 图5 四艘某型舰编队PS随Rx和H的变化曲线表2 目标高度为100m时Rx的最优值(链) 舰数舰型345舰型Ⅲ7~910~1113~16舰型Ⅱ5~89~1112~16舰型Ⅰ7~910~1213~16 表3 目标高度为1000m时Rx的最优值(链) 表4 目标高度为2000m时Rx的最优值(链) 从算例计算结果可以看出: 1) 警戒幕上舰数越多,Rx的最优值越大。 2) 目标的高度越高,Rx的最优值越小。 3)Rx的最优值与表中所列三种舰无关。实际计算表明,Rx的最优值与舰种没有直接关系,而与主、副炮的拦截距离有很大关系。 4) 不同舰种的主、副炮数量对PS的绝对值有影响,但不影响PS随Rx的变化规律。由此可见,即使A1、B2的定义不严格,也不会影响数学模型的最后计算结果。 本文给出一种舰艇编队防空队形配置模型,并通过算例验证了模型的合理性。考虑到目标的来袭高度一般不高,有理由根据计算结果认定:对3、4、5艘警戒舰三种情况,警戒幕半径Rx应分别为8、10、14链,这样配置的警戒幕队形可获得最好的对空防御效果。 本文算例虽然仅以某型主炮和副炮为例,但模型对于装备其它型号舰炮的舰艇同样有效,只要改变一下火炮拦截距离及死区的数据就可以了。 由于在计算过程中所使用的单发炮弹对飞机的毁伤概率是近似的,所以算出的PS值也是近似的,但这并不影响PS随Rx的变化规律。 本文给出的毁伤概率计算模型是对飞机而言的。对于高度较低的来袭导弹,为保证友舰的安全,警戒舰不宜向编队内部射击。这种情况下,Rx应小一点,以保证有足够的火力交叉射击时间。 此外,在本文提供的数学模型中,PS计算只考虑与目标航路相邻两警戒舰的抗击情况,实际上被警戒舰船也进行抗击,但这种抗击对寻求Rx的最优值无影响,所以在计算中不作考虑。 [1] 谭安胜.水面舰艇编队作战运筹分析[M].北京:国防工业出版社,2009. [2] Orhan K, Nur E O, Levent K. Anti-Ship Missile Defense for a Naval Task Group[J]. Naval Research Logistics,2011,58(2):306-321. [3] Washburn A. The Bang-Soak Theory of Missile Attack and Terminal Defense[J]. Military Operations Research,2005,10(1):15-23. [4] 赵国钢.驱护舰编队防空火力分配决策模型研究[D].大连:海军大连舰艇学院,2007. [5] 赵建印,刘芳.海上编队双舰防空队形部署优化研究[J].兵工学报,2010,31(2):865-869. [6] 马洪磊.编队队形变换与保持方法研究[D].大连:海军大连舰艇学院,2009. [7] 李铁.近炸引信预制玻片弹对空作战使用研究[D].大连:海军大连舰艇学院,2001. [8] 王连柱.舰炮对空战斗使用[M].大连:海军大连舰艇学院,2009. [9] 汪德虎,谭周寿.舰炮射击基础理论[M].北京:海潮出版社,1998. [10] 过传义,等.舰炮武器系统射击效力评定[M].北京:海军装备论证中心,1992. Formation Configuration for Convoy Warship Group JIANG Ludong1SUN Jianhua2YU Jiaxiang2 (1. Naval Equipment Department, Beijing 100071)(2. Dalian Naval Academy, Dalian 116018) To meet the needs for air defense of convoy warship group, a formation configuration method is presented from a quantitative point of view. In the method, the ship-borne gun are the unique anti-air weapons, and the alarm radius is the optimization target, and the mathematical model for formation configuration of convoy warship group is constructed. The model is demonstrated to be valid by computational examples in which typical warships and ship-bornes are regarded as input parameters. warship, task group, formation configuration 2013年8月3日, 2013年9月25日 中国博士后科学基金(编号:2012M521893)资助。 姜鲁东,男,硕士,工程师,研究方向:舰载武器系统及作战使用。 O212.8 10.3969/j.issn1672-9730.2014.02.005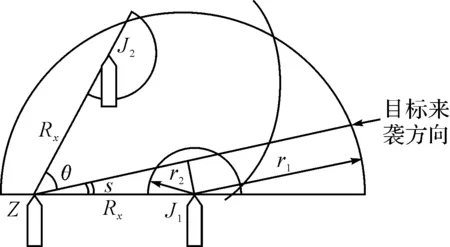
4 算例






5 结语

