黏弹阻尼层设计参数对阻尼填充墙框架抗震性能的影响分析*

廖奕发，郭阳照，杨冠男，周 云

(广州大学土木工程学院，广东广州510006)

0 引言

阻尼填充墙(Damped Infill Wall，简称DIW)是国内近年提出的一种新型减震墙体(周云，郭阳照，2011)。研究表明阻尼填充墙通过砌体单元间黏弹阻尼层剪切滞回变形耗能，具有良好的耗能效果，能为框架提供一定的抗侧力，提高结构的水平承载力，减缓结构的承载力衰减，而且不过强约束框架变形，避免造成框架柱受剪破坏、框架结构变形能力和延性变差的不利影响(郭阳照等，2013;周云等，2010，2013a，b)。

黏弹阻尼层的设计是DIW设计的核心内容，其合理性决定着阻尼填充墙框架(Damped Infill Wall Frame，DIWF)的减震性能。本文采用ABAQUS软件对不同黏弹阻尼层设计参数的DIWF进行分析，研究黏弹阻尼层储能剪切模量、厚度和损耗因子对DIWF抗震性能的影响，并给出相关的设计建议。

1 模型设计

笔者设计了3组共18个单层单跨的阻尼填充墙框架模型。各模型的区别仅在于黏弹阻尼层参数的不同，其主体框架参数均相同，具体如下:框架跨度为6 000 mm，层高为3 000 mm，如图1所示;柱截面为500×500 mm2，梁截面为300×600 mm2;混凝土强度等级为C30;梁、柱配筋根据《混凝土结构设计规范》(GB50010－2010)和《建筑抗震设计规范》(GB50011－2010)的相关要求进行设计，具体见图2。

阻尼填充墙由3个砌体单元和4层黏弹阻尼层构成，黏弹阻尼层设于上下相邻砌体单元间、顶层砌体单元与框架顶梁间以及底层砌体单元与底梁间(图1);砌体单元的一侧用拉结筋连接固定于框架柱(上下相邻砌体单元异侧固定)，而另一侧与另一柱间预留50 mm的缝隙，用柔性连接;墙体厚度为180 mm，砌体平均抗压强度为8 MPa。

图1 DIWF构造示意图Fig.1 Construction schematic of DIWF

每组分析模型的数量均为6个。第Ⅰ组为黏弹阻尼层储能剪切模量对比分析组，储能剪切模量的取值见表1，各模型的黏弹阻尼层厚度和损耗因子相同，分别为10 mm和0.25;第Ⅱ组为黏弹阻尼层厚度对比分析组，厚度的取值如表1所示，各模型的黏弹阻尼层储能剪切模量和损耗因子均相同，分别为0.1 MPa和0.25;第Ⅲ组为黏弹阻尼层损耗因子对比分析组，损耗因子的取值如表1所示，各模型的黏弹阻尼层储能剪切模量和厚度相同，分别为0.1 MPa和10 mm。

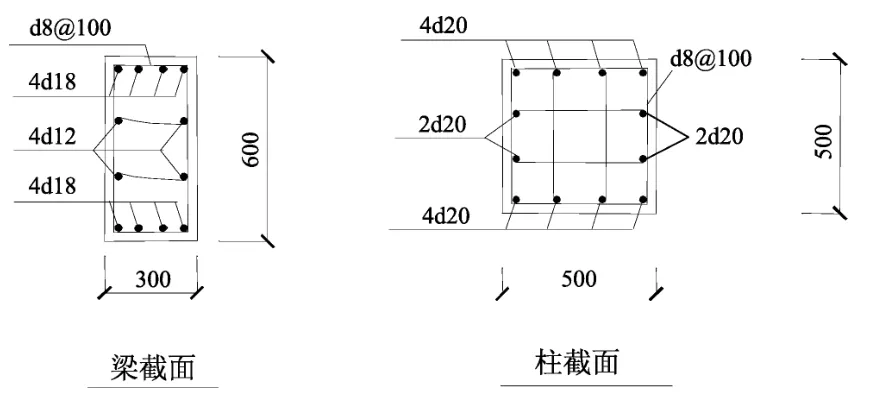
图2 梁柱截面及配筋Fig.2 Cross-section and reinforcement of beam and column

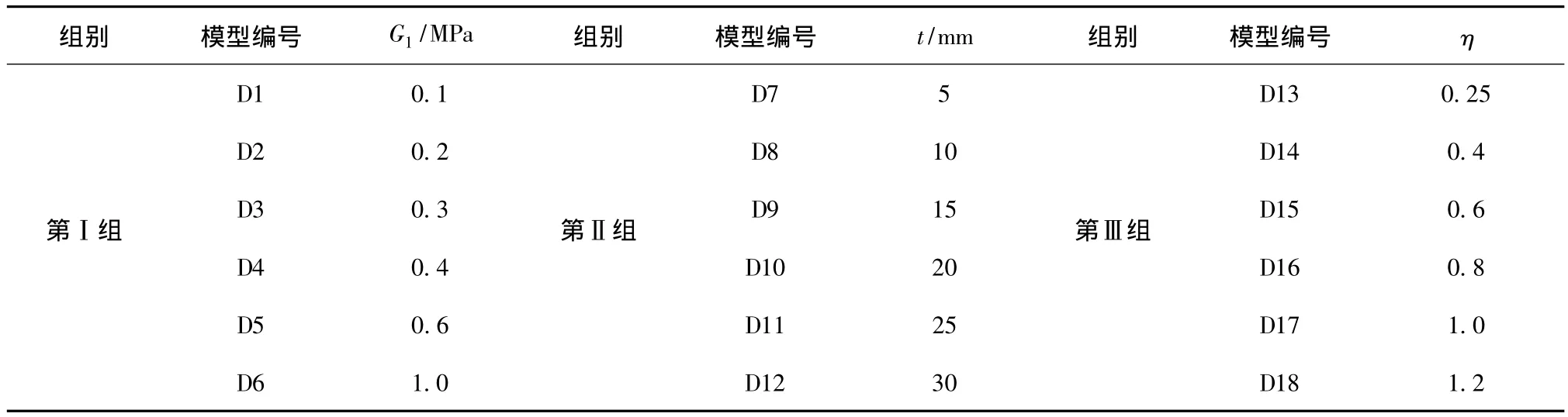
表1 黏弹阻尼层G1、t及η的取值情况Tab.1 Values of G1 ，t and η of viscoelastic damped layer

2 有限元模型的建立与验证

2.1 主体框架

参考郭阳照等(2013)，Singh(1998)等的研究，框架梁、柱均采用纤维梁单元模拟。混凝土本构方程见式(1)(Silvia mazzoni，et al 2006)，钢筋本构选用等方向性强化规则的Menegotto-Pinto模型(Martinez-Rueda，Einashai，1997;Monti，Nuti，1973;Filippo et al，1983)，其表达见式(2)。

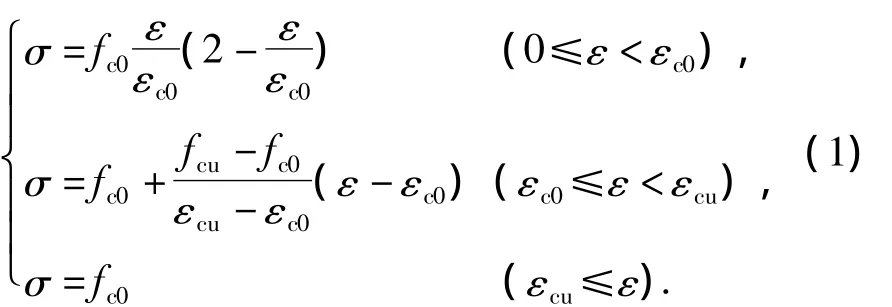
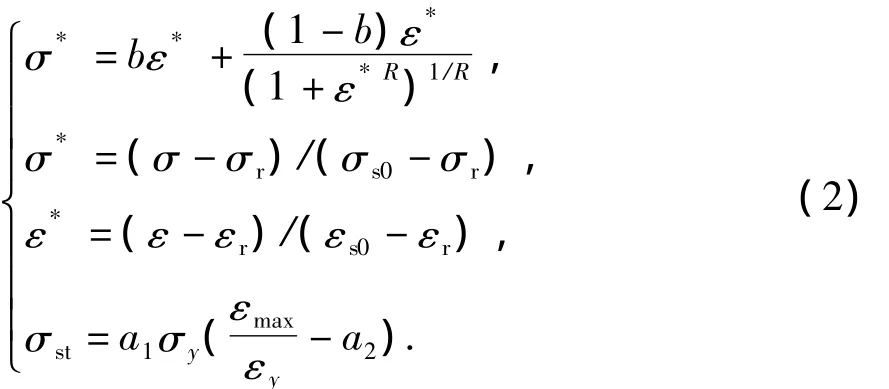
式中，σs0和εs0分别为斜率等于初始弹模E0和Esp=bE0两渐近直线交点处的应力和应变值;σγ和εγ为最后一次应变逆转点的应力和应变值;b为应变强化系数;R为控制过渡曲线形状参数;σst是一次荷载循环后变化的屈服应力;εmax为当前应变循环最大绝对应变值;σy和εy为屈服应力和应变;参数a1和a2分别定义等方向性强化的程度和临界值。

2.2 砌体

参考郭阳照等(2013)，Ghosh和 Amde(2002)的研究，将砌体视为各向同性匀质材料，采用平面应力单元划分。砌体本构选用两段式本构模型(朱伯龙，1998):

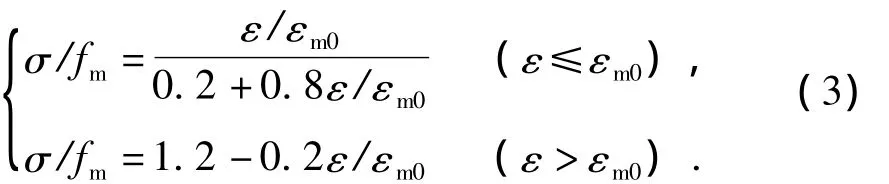
式中:σ、ε分别为砌体材料的应力和应变;fm为砌体抗压强度平均值;εm0为峰值应力对应的应变。

2.3 黏弹阻尼层

黏弹阻尼层采用多个Kelvin模型模拟，如图3所示，用线性弹簧元件LS1表征黏弹阻尼层的弹性恢复特性，用黏壶元件NH1表征黏弹阻尼层的黏滞阻尼性能。弹簧LS1的剪切刚度系数k和黏壶NH1的阻尼系数 c的确定计算如下(周云，2006):

式中:G1为黏弹阻尼层的储能剪切模量;As为黏弹阻尼层的水平横截面面积;t为黏弹阻尼层的厚度;n为Kelvin模型的个数;η为黏弹阻尼层的损耗因子;ω为激励频率。

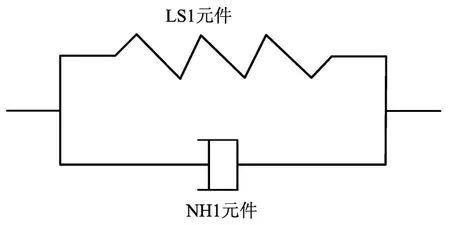
图3 Kelvin模型Fig.3 Model of Kelvin

2.4 砌体—框架界面接触

砌体—框架柱间的界面采用摩擦接触(Mohebkhah et al，2008)，摩擦系数设为0.7(砌体结构设计规范，2011)。拉结筋采用杆单元模拟。

2.5 数值模型合理性验证

采用上述方法建立BF试件和DIWF试件的有限元模型(周云等，2013b)，并进行仿真分析。图4给出了BF试件和DIWF试件的计算模拟结果与试验结果的对比图。

(1)计算的BF滞回曲线、骨架曲线与试验结果吻合得较好(图4a，b)，峰值荷载计算值与试验值的误差在10%以内，初始刚度的误差在2%左右。表明纤维梁单元模型能够较好地模拟空框架在水平循环荷载作用下的反应。

昨天一个采访延误，我来不及赶回家做晚饭，就打电话给乔振宇让他先去新开的一家韩餐馆点餐等我。等我赶到时，排号等座等了一个小时的乔振宇跟值班经理已经吵得脸红脖子粗，食客们有围观的有瞎起哄的。

(2)计算的DIWF滞回曲线、骨架曲线同样能够较好地吻合试验结果(图4c，d)，峰值荷载和初始刚度的计算值与试验值的误差均在5.0%以内，计算的误差较小。

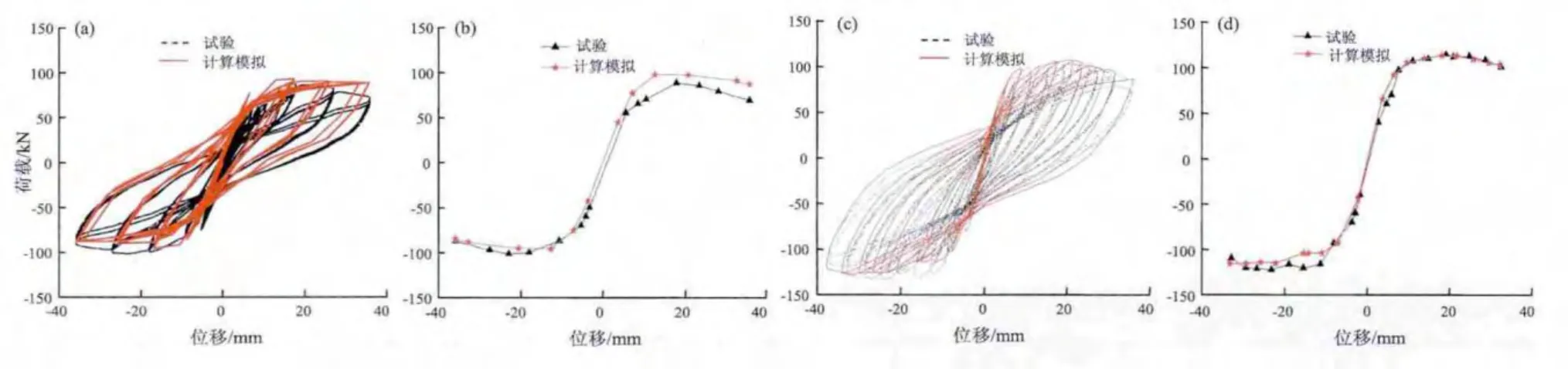
图4 计算模拟结果与试验结果对比(a)BF滞回曲线;(b)BF骨架曲线;(c)DIWF滞回曲线;(d)DIWF骨架曲线Fig.4 Comparison of numerical simulation and test results(a)hysteretic curve of BF;(b)skeleton curve of BF;(c)hysteretic curve of DIWF;(d)skeleton curve of DIWF

3 结果分析

3.1 黏弹阻尼层储能剪切模量影响分析

图5和图6分别给出了第Ⅰ组DIWF分析模型的滞回曲线和骨架曲线。由图可知:

(1)各模型的滞回曲线饱满，滞回特性稳定，滞回环包络的面积随加载位移的增大而增大，滞回环呈梭形，无明显的捏缩效应。

(2)黏弹阻尼层的储能剪切模量大于0.3 MPa时，滞回曲线正反向不对称的现象较为明显。原因是黏弹阻尼层储能剪切模量较大，阻尼填充墙对两侧框架柱的约束作用存在较大差异。

(3)黏弹阻尼层储能剪切模量对DIWF的抗侧刚度和水平承载力有较大的影响。储能剪切模量由0.1 MPa增大至1 MPa时，DIWF的初始刚度由65 kN/mm增大至92 kN/mm，峰值荷载由1 236 kN增大至2 271 kN。表明黏弹阻尼层储能剪切模量越大，阻尼填充墙对框架的抗侧刚度和抗侧力的贡献越大，DIWF的初始刚度和峰值荷载越大。

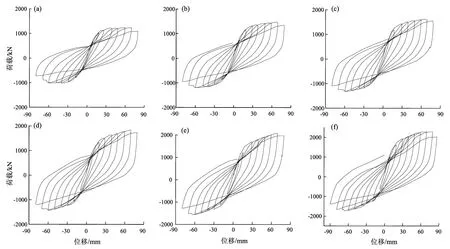
图5 第Ⅰ组DIWF模型的滞回曲线(t=10 mm，η=0.25)(a)D1(G1=0.1 MPa);(b)D2(d1=0.2 MPa);(c)D3(G1=0.3 MPa);(d)D4(G1=0.4 MPa);(e)D5(G1=0.6 MPa);(f)D6(G1=1.0 MPa)Fig.5 Hysteretic curves of DIWF model in groupⅠ(t=10 mm，η=0.25)

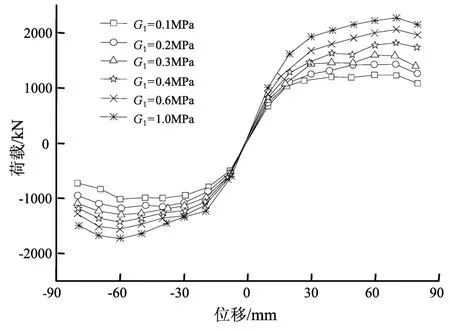
图6 第Ⅰ组DIWF模型的骨架曲线Fig.6 Skeleton curve of DIWF model in groupⅠ

根据《建筑抗震试验方法规程》(JGJ01－1996)中第4.5.6条的方法，计算DIWF的等效黏滞阻尼系数。图7a给出了DWIF在极限状态下的等效黏滞阻尼系数随黏弹阻尼层储能剪切模量变化的曲线。由图可知，随着黏弹阻尼层储能剪切模量的增大，DIWF的等效黏滞阻尼系数先增大后减小;储能剪切模量为0.3 MPa时，等效黏滞阻尼系数达到最大，为0.29。可见，黏弹阻尼层的储能剪切模量大于0.3 MPa时，DIWF的耗能能力下降。其原因是，储能剪切模量大于0.3 MPa时，阻尼层的剪切变形很小(图7b)，其耗能量变小(图7c)，耗能效果变差。

图8为阻尼填充墙典型的mises应力分布云图。由图可见，框架发生侧移时，顶层砌体单元左上角部的应力最大。图9给出了第Ⅰ组DIWF模型在层间位移角为1/550时，墙体的最大mise应力随黏弹阻尼层储能剪切模量变化的曲线。由图可知，黏弹阻尼层储能剪切模量增大，墙体的mise应力不断增大，墙体较容易破坏。

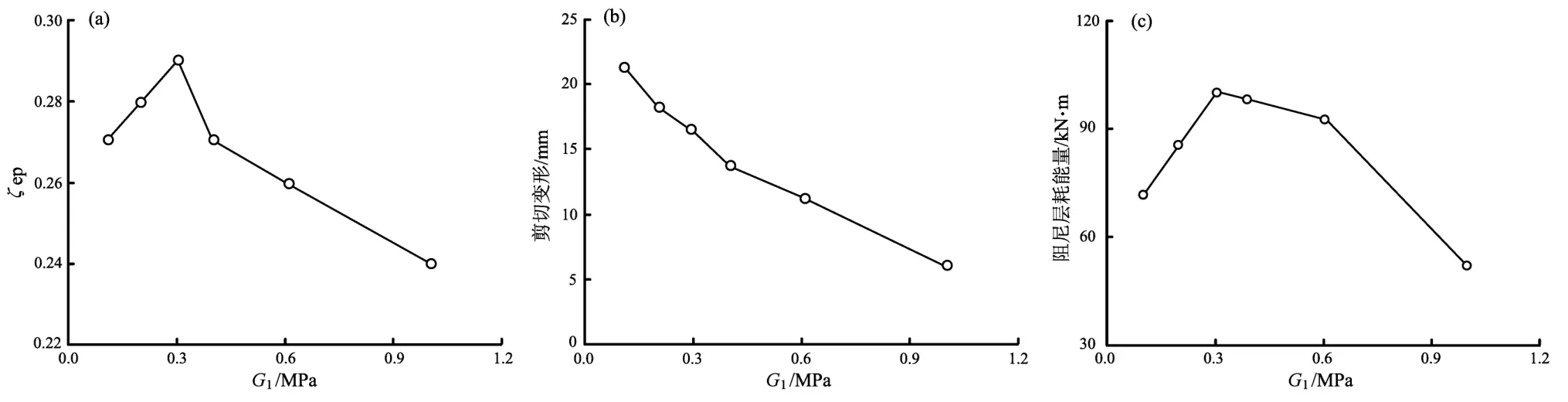
图7 第Ⅰ组DWIF模型的等效黏滞阻尼系数(a)、剪切变形(b)、耗能量(c)变化曲线Fig.7 Variation curve of equivalent viscoelastic damping coefficient(a)，shear deformation(b)and energy-dissiptated(c)of DWIF model in groupⅠ

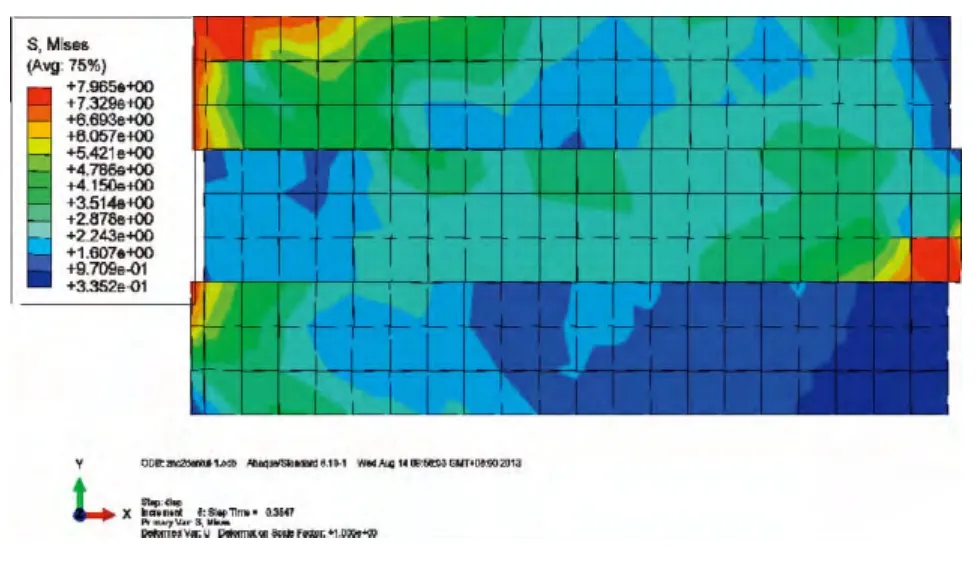
图8 阻尼填充墙mises应力分布Fig.8 Mises stress distribution of DIW

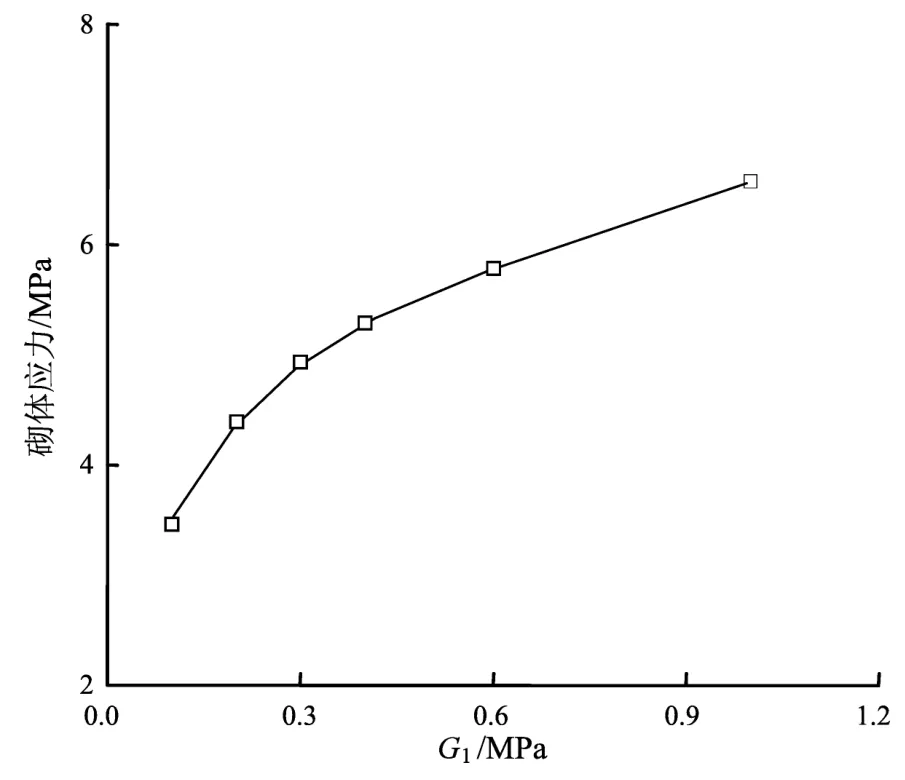
图9 第Ⅰ组DWIF模型mises应力变化曲线Fig.9 Variation curve of mises stress of DWIF model in groupⅠ

3.2 黏弹阻尼层厚度影响分析

图10给出了第Ⅱ组的D7、D10和D12模型的滞回曲线。由图可知，黏弹阻尼层储能剪切模量

图10 第Ⅱ组D7(a)、D10(b)和D12(c)模型的滞回曲线(G1=0.1 MPa，η=0.25)Fig.10 Hysteretic curves of D7(a)，D10(b)and D12(c)models in groupⅡ(G1=0.1 MPa，η=0.25)

综上所述，增大黏弹阻尼层的储能剪切模量有利于提高DIWF的抗侧刚度和水平承载能力，但黏弹阻尼层的储能剪切模量大于0.3 MPa时，阻尼填充墙对两侧框架柱的约束作用存在较大差异，DIWF的耗能能力随着阻尼层储能剪切模量的增大而降低;此外，墙体也较容易发生破坏。为此，建议黏弹阻尼层的储能剪切模量不宜大于0.3 MPa。和损耗因子相同时，阻尼层厚度越大，DIWF的滞回曲线越来越不饱满。

图11给出了第Ⅱ组DIWF模型的骨架曲线。由图可知，黏弹阻尼层的厚度越大，DIWF的抗侧刚度和水平承载力越小。当厚度由5 mm增大至15 mm时，DIWF的初始刚度和峰值荷载降低的幅度较大，其中，初始刚度由78 kN/mm减小至67 kN/mm，峰值荷载由1 425 kN减小至1 079 kN;而黏弹阻尼层厚度由15 mm增大至30 mm时，DIWF的初始刚度和峰值荷载变化较小，初始刚度由67 kN/mm减小至66 kN/mm，峰值荷载由1 056 kN减小至1 046 kN。

图12a给出了DIWF在极限状态下的等效黏滞阻尼系数随黏弹阻尼层厚度变化的曲线图。由图可知，当黏弹阻尼层厚度由5 mm增大至15 mm时，DIWF的等效黏滞阻尼系数由0.33减小至0.3，减小幅度较大;而阻尼层厚度大于15 mm时，等效黏滞阻尼系数变化较小，由0.29减小至0.28。可见，阻尼层厚度越大，DIWF的等效黏滞阻尼系数越小。原因在于，黏弹阻尼层厚度增大，阻尼层的剪切应变减小(图12b)，其耗能量降低(图12c)，耗能效果变差。

图11 第Ⅱ组DIWF模型的骨架曲线Fig.11 Skeleton curve of DIWF model in groupⅡ

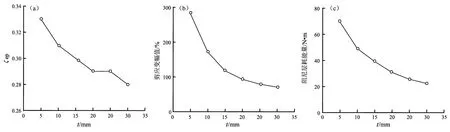
图12 第Ⅱ组DIWF模型的等效黏滞阻尼系数(a)，剪应变幅值(b)，耗能量(c)变化曲线Fig.12 Variation curve of equivalent viscoelastic damping coefficient(a)，shear deformation amplitude(b)and energy-dissiptated(c)of DIWF model in groupⅡ

由上述分析可知，通过调整黏弹阻尼层的厚度，可以控制DIWF的抗侧刚度、水平承载力和耗能能力;当黏弹阻尼层厚度在5～15 mm之间变化时，DIWF的刚度、承载力和耗能性能的变化较大;当厚度在15～30 mm变化时，DIWF性能的变化幅度很小。另一方面，黏弹阻尼层的剪应变幅值随着层厚度的减小而不断增大，当阻尼层厚度为5 mm时，其剪应变幅值为281%，接近黏弹材料的极限剪应变300%、周云(2006)研究表明黏弹阻尼材料大于300%时发生剪切破坏。基于上述考虑，建议黏弹阻尼层的厚度宜控制在5～15 mm之间。

3.3 黏弹阻尼层损耗因子影响分析

图13给出了第Ⅲ组的D13、D15和D18模型的滞回曲线。由图可知，各模型的滞回曲线饱满，滞回性能稳定，滞回环呈梭形，无明显的捏缩效应;随着黏弹阻尼层损耗因子的增大，滞回曲线越趋饱满。

图14给出了第Ⅲ组DIWF模型的骨架曲线。由图可见，黏弹阻尼层的损耗因子不断增大时，DIWF的初始刚度变化不大，峰值荷载小幅上升。

图15给出了DIWF在极限状态下的的等效黏滞阻尼系数随黏弹阻尼层损耗因子变化的曲线。由图可知，黏弹阻尼层损耗因子的增大，DIWF的等效黏滞阻尼系数不断增大，由0.31增大至0.38，DIWF的耗能能力明显增强。因此，应选择损耗因子大的黏弹材料制作黏弹阻尼层。

图13 第Ⅲ组D13(a)、D15(b)和D18(c)模型滞回曲线(G1=0.1 MPa，t=10 mm)Fig.13 Hysteretic curves of D13(a)，D15(b)and D18(c)models in groupⅢ(G1=0.1 MPa，t=10 mm)

图14 第Ⅲ组DIWF模型的骨架曲线Fig.14 Skeleton curve of DIWF model in groupⅢ

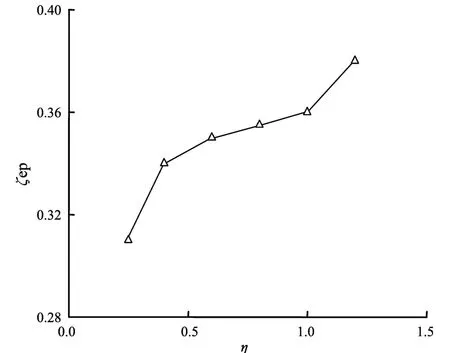
图15 第Ⅲ组DIWF模型的等效黏滞阻尼系数变化曲线Fig.15 Curve of equivalent viscoelastic damping coefficient variation of DIWF model in groupⅢ

4 结论与建议

(1)黏弹阻尼层的储能剪切模量、厚度和损耗因子对DIWF的抗震性能均有较大影响，应对其进行合理设计。

(2)随着黏弹阻尼层储能剪切模量的增大，DIWF的抗侧刚度和水平承载能力有所提高，但黏弹阻尼层的储能剪切模量过大时，黏弹阻尼层的剪切变形很小，DIWF的耗能能力明显降低，而且墙体容易发生破坏。建议黏弹阻尼层的储能剪切模量不宜大于0.3 Mpa。

(3)随着黏弹阻尼层厚度的增大，DIWF的抗侧刚度、水平承载力和耗能能力均呈下降趋势;适当减小黏弹阻尼层的厚度，有助于提高结构的滞回耗能性能，还可减少黏弹材料的用量，降低工程造价，但过薄的黏弹阻尼层不能满足剪切变形要求。黏弹阻尼层的厚度宜控制在5～15 mm之间。

(4)黏弹阻尼层损耗因子的变化主要影响DIWF的耗能性能，黏弹阻尼层的损耗因子越大，DIWF的耗能能力越强。设计时，应选择损耗因子大的黏弹材料制作黏弹阻尼层。

衷心感谢周云教授和郭阳照博士对本次工作的耐心指导和热心帮助。

郭阳照，周云，甘英杰，等.2013.新型框架阻尼填充墙性能分析［J］.振动与冲击，32(14):127－133.

周云，郭阳照，廖奕发，等.2013a.阻尼填充墙单元性能试验研究［J］.土木工程学报，46(5):56 －63.

周云，郭阳照，杨冠男，等.2013b.阻尼砌体填充墙框架结构抗震性能试验研究［J］.建筑结构学报，34(7):89－96.

周云，郭阳照.2011.一种用于框架结构的阻尼抗震填充墙板［P］.中国专利:CN102268900A，06.11.

周云，彭水淋，尹庆利，等.2010.新型框架阻尼填充墙的设计与分析［J］.工程抗震与加固改造.33(4):79－83.

周云.2006.粘弹性阻尼减震结构设计［M］.武汉:武汉理工大学出版社.

朱伯龙.1998.砌体结构设计原理［M］.上海:同济大学出版社.

Mohebkhah A.，Tasnimi A.A.，Moghadam H.A..2008.Nonlinear analysis of masonry-infilled steel frames with openings using discrete element Method［J］.Constructional steel research，64(12):1463－1472.

Filippo F.C.，Popov E.P.，Bertero V.V..1983.Effects of bond deterioration on hysteretic behavior of reinforced concrete joints［R］.USA:Earthquake Engineering Research Centre，University of California Berkeley.

GB50003－2011，砌体结构设计规范［S］.

GB50010－2010，凝土结构设计规范［S］.

GB50011－2010，建筑抗震设计规范［S］.

Ghosh A.K.，Amde A.M.，2002.Finite element analysis of infilled frames［J］.Struct Engineering，128(7):881 － 889.

JGJ01－1996，建筑抗震试验方法规程［S］.

Martinez-Rueda J.E.，Einashai A.S..1997.Confined concrete model under cyclic load［J］.Materials and Structures，30(4):139 － 147.

Monti G.，Nuti C..1973.Method of analysis for cyclically loaded R.C plane frames including changes in geometry and nonelastic behavior of elements under combined normal force and bending［J］.Symposium on Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads，International Association for Bridge and Structural Engineering，Zurich，Switzerland:15 －22.

Silvia mazzoni，Frank Mckenna，Michanel H.Scott，et al.2006.Open System for Earthquake Engineering Simulation User Command-Language Manual，University of California Berkeley.

Singh H.，Paul D.K.，Sastry V.V..1998.Inelastic dynamic response of reinforced concrete infilled frames［J］.Comput＆ Structure，69(6):685－693.