天津市测震台网Sg震相到时残差大的原因分析*

谢 静，刘双庆，谭毅培

(天津市地震局，天津300201)

0 引言

地震定位是地震学研究中首要和最基本的问题之一。精确的定位不仅能够保证区域台网观测报告的准确性和完整性，也能为地震分析预报工作提供科学的基础资料。在常用的线性化地震定位方法中，走时表或速度结构模型的选取对定位结果有较大影响(Bouchaala et al，2013;Mahesh et al，2013)，即使如主事件定位法、双差定位法(Waldhauser，Ellsworth，2000)等相对定位方法，选取不同的1维速度模型仍会造成定位结果明显的偏差(Michelini，Lomax，2004)。虽然有研究表明，使用三维速度结构模型能有效提高定位精度(Chen，Willemann，2001;张慧民等，2013)，但其定位算法计算复杂度较高，且需要研究区域有普遍认可的三维速度模型。因此在区域地震台网日常编目工作中，选取合适的一维多层地壳速度结构模型来有效提高地震定位精度，是切实可行的办法。

本文以天津测震台网地震记录为例，针对定位结果中Sg震相正残差整体偏大的问题，选取多种一维速度模型计算理论到时，与观测到时比较，分析不同一维速度模型对Sg到时以及地震定位精度的影响。然后在不改变速度模型的基础上，分析震源深度的改变对Sg震相到时的影响。

1 台站及数据资料

本研究选取2009年1月至2012年3月天津市行政区内ML≥1.0及其邻区ML≥2.0的49个地震，重新进行震相到时读取。所选地震目录来自中国地震台网中心，地震波形数据及台站信息源于天津测震台网。天津测震台网台站分布及所选地震分布情况见图1。

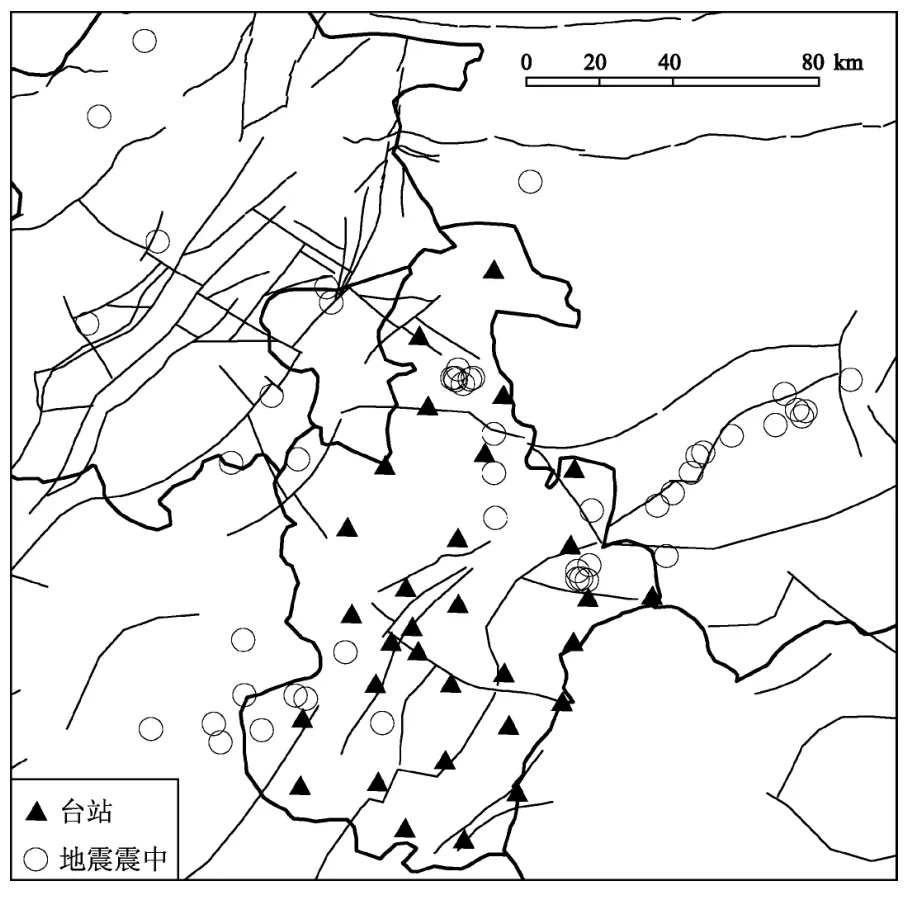
图1 地震与台站分布Fig.1 Distribution of the selected earthquakes and stations

震相读取时只选取天津测震台网台站记录到的清晰震相到时，并将该到时称为震相的读取到时。本文所选取的6种速度模型如表1所示，所有速度模型每层内地震波速度是均匀的。对每一种速度模型计算地震的Pg和Sg震相理论到时，与读取到时相减以获得各个速度模型定位台站的Pg和Sg到时差，并用这些结果分析检验不同速度模型对Pg和Sg震相到时的影响。

表1 地壳模型与地震波速度结构模型Tab.1 Crust model and velocity structure model of seismic wave

2 结果分析

通过对所选地震进行重新定位，从定位报告里提取各个台站的Pg、Sg震相走时及其对应的震中距，可以分别得到天津地区Pg、Sg震相的走时与震中距关系，如图2所示，实线为拟合曲线，拟合后获得天津地区的平均速度模型和震源优势深度:VP=5.99 km/s，VS=3.48 km/s，H=13 km，这就是表1里的速度模型1。

这个震源优势深度与张国民等(2002)通过研究各省区域地震台网结果获得的华北地区平均震源深度(14±7)km的结果基本一致，比郭永霞等(2010)认为华北地区震源深度主要分布在7.5～12.5 km范围内要略深。编目工作中所用的华南速度模型(表1中速度模型4)和该平均速度模型相比，S波速度明显偏大，必然会导致地震波理论到时偏前。

已知速度模型、震源位置、台站位置就可以计算出地震波从震源到台站的理论走时，再结合发震时刻就可以得到地震波到达每个台站的理论到时。本文只讨论不同速度模型、不同震源深度对地震波的直达波Pg、Sg震相定位残差的影响，这里用Pg、Sg震相读取到时与理论到时之差来衡量定位残差大小。本文用4种震源深度来进行讨论:第1种是单纯型法定位所得震源深度，一般为5 km、6 km，简称深度1;第2种是所有地震在深度1基础上增加5 km，震源深度平均在10 km左右，简称深度2;第3种是所有地震在震源深度1基础上增加10 km，震源深度值大致在15 km左右，简称深度3;第4种是所有地震在震源深度1基础上增加15 km，震源深度值大致在20 km左右，简称深度4。

图3是6种不同速度模型的Pg到时差分布图。图3a震源深度为深度1时，中心点在－0.5附近，到时差值主要分布在(－1，1)，说明速度模型1的P波速度值与实际相比略有偏差，因为本文采用的速度结构是均匀层状速度模型，与实际地下结构有差异，因此导致到时差值有正值也有负值。随着震源深度的加深，Pg到时差分布图的中心点从0向－1移动，说明速度模型1在震源深度值较小时比较符合实际，在震源深度值较大时，速度值偏小，震源深度值对震相到时的影响，主要原因可能是速度模型的不合理造成的。图3b震源深度为深度1时，中心点在0值附近，到时差值主要分布在(－1，1)，说明速度模型2的P波速度值比较符合实际，此时4种震源深度所得Pg到时差值都集中分布在0值附近，速度模型2较适合天津地区的速度模型，该模型下震源深度对震相到时影响较小。图3c震源深度为深度1时，中心点在－1附近，到时差值主要分布在(－2，1)，速度模型3的P波速度值偏小。该模型下，震源深度为深度4到时差分布中心点在－0.5附近，比其它3种深度到时差值略小。说明在该速度模型下，震源深度在20 km左右时，理论到时和实际到时比较接近。但相对速度模型对震相到时的影响而言，震源深度对震相到时的影响很小。图3d震源深度为深度1时，中心点在0附近，到时差值主要分布在(－1，1)，速度模型4的P波速度值也比较符合实际，该速度模型是编目工作常用的华南速度模型，因此在编目工作中Pg震相并未出现到时残差较大的现象。在该速度模型下，4种震源深度所得Pg到时差值都集中分布在－0.2附近，该P波速度模型较符合天津地区，此时震源深度对震相到时影响并不大。图3e震源深度为深度1时，中心点在 －0.5附近，到时差值主要分布在(－1.5，0.5)，速度模型5的P波速度值较实际值略微偏小。在该速度模型下，4种震源深度所得Pg到时差值都集中分布在－0.5附近，震源深度对震相到时影响并不大。图3f震源深度为深度1时，中心点在－1.5附近，到时差值主要分布在(－3，0.5)，速度模型6的P波速度值与实际值相差甚远，可见全球速度模型并不适合于局部地区。在该速度模型下，震源深度在15 km左右时，Pg到时差分布图中心点在－0.5附近，而震源深度为20 km时，中心点在－1附近，震源深度在0～10 km时，中心点在－1.5附近，在该速度模型下震源深度对震相到时影响较大，其原因可能是速度模型的不合理。从Pg到时差分布图分析，速度模型2、速度模型4的P波速度值是较适合天津地区的，在这两种速度模型下，震源深度对Pg到时影响并不大。

图4是6种不同速度模型的Sg到时差分布图。图4a中震源深度为深度1时，中心点在0附近，到时差值主要分布在(－1，1)，对速度模型1，随着震源深度的加深，Sg到时差分布的中心点从0向－1移动，说明该平均速度值在震源深度浅时比较符合实际，在震源深度值较大时，速度值偏小，震源深度值对震相到时的影响，主要原因可能是速度模型的不合理造成的。图4b中震源深度为深度1时，中心点在0值附近，到时差值主要分布在(－1，1)，速度模型2的S波速度值符合天津地区，在该速度模型下，4种震源深度所得Sg到时差值变化不大，说明此时震源深度对震相到时影响不大。图4c中震源深度为深度1时，中心点在 －0.5，到时差值主要分布在(－2，1)，说明速度模型3的S波速度值偏小，在该速度模型下，4种震源深度所得Sg到时差值变化不大;图4d中震源深度为深度1时，中心点在0.8附近，到时差值主要分布在(－1，2)，速度模型4的S波速度值偏大，日常编目工作应用的是该模型，因此，理论的Sg震相到时比实际读取的到时早，导致了Sg到时残差大，这与工作中碰到的现象相符。在该速度模型下，4种震源深度所得Sg到时差值变化并不大。图4e震源深度为深度1时，中心点在－1附近，到时差值主要分布在(－2，1)，速度模型5的S波速度值偏小;在该速度模型下，4种震源深度所得Sg到时差值变化并不大。图4f中震源深度为深度1时，中心点在－1附近，到时差值主要分布在(－3，1);震源深度为深度3、深度4时，中心点在－0.2值附近，震源深度越深该速度模型所得Sg到时差值越小;该速度模型为全球速度模型，与局部速度结构相差甚远，可能导致了震源深度对震相到时的较大影响。从Sg到时差分布图分析，速度模型2的S波速度值是比较适合天津地区的。结合P波速度值和S波速度值的分析，只有速度模型2是比较适合天津地区的。大多数速度模型下，震源深度对震相到时的影响并不大，震源深度对震相到时的影响比上述的速度模型差异对震相到时的影响小得多。

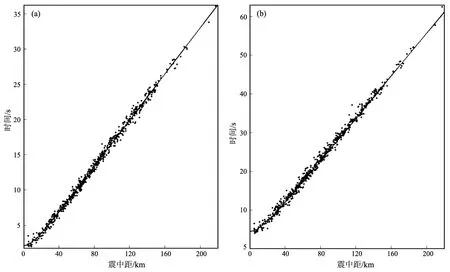
图2 Pg(a)、Sg(b)震相的走时与震中距关系图Fig.2 Relationships between time and distance of Pg(a)and Sg(b)phases

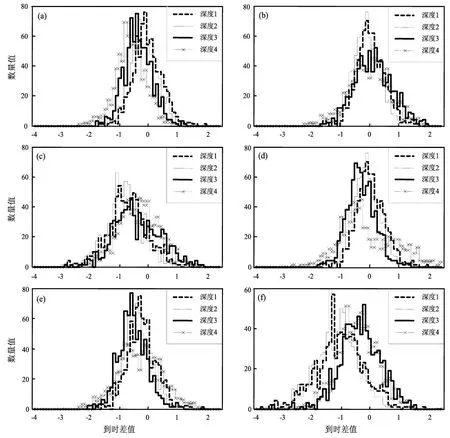
图3 6种速度模型的Pg震相到时差分布图Fig.3 The distribution of six kinds of velocity models corresponding to arrival time differences of Pg phase

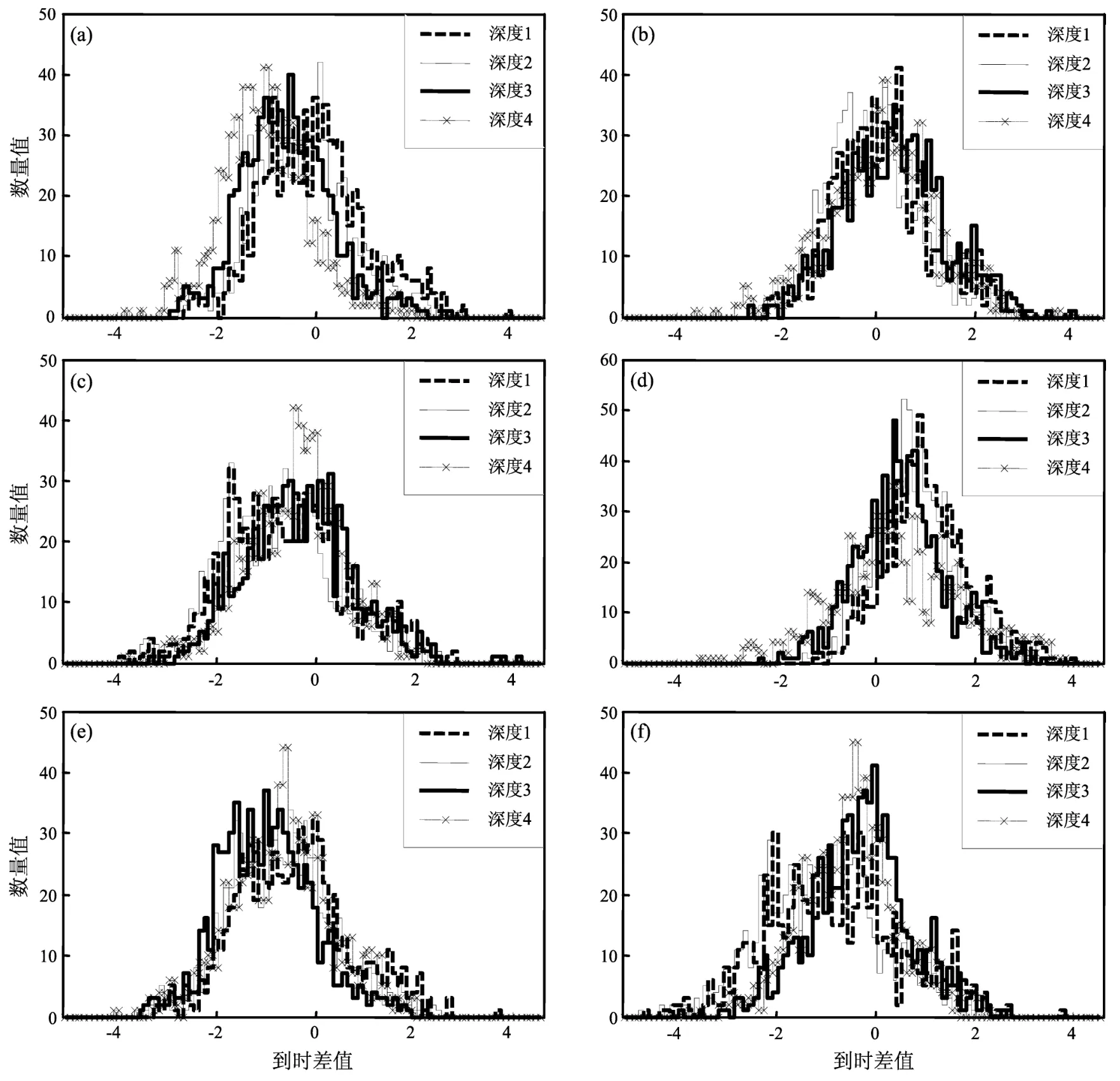
图4 6种速度模型的Sg震相到时差分布图Fig.4 The distribution of six kinds of velocity models corresponding to arrival time differences of Sg phase

3 结论与认识

(1)天津测震台网日常编目所用软件MSDP定位时所用的速度模型是华南速度模型(速度模型4)，通过分析可知，华南速度模型P波速度比较符合天津地区，因此在编目中Pg震相到时残差较小;而华南速度模型S波速度值较天津地区偏大，导致了Sg震相理论到时比实际到时超前。因此，该速度模型并不很适合天津地区。通过本文的分析研究可知本文所列出的6个模型中，速度模型2是比较符合天津地区的，在今后编目工作中，可以用该速度模型替换现用的速度模型4。

(2)从本文的分析结果看，引起震相到时残差大的原因主要是速度模型的不合理。在速度模型较合理时，震源深度对震相到时残差的影响并不明显，影响较大的主要是震中距较小的近台震相走时;速度模型与实际情况相差甚远时，震源深度对震相到时残差的影响将变大，因此震源深度对震相到时残差的影响可能很大程度上受速度模型的合理性控制。

(3)本文通过对所选地震的直达P波和S波的走时曲线的分析，得到天津及邻近地区地震的平均优势震源深度在13 km左右，而实际工作中单纯型法定位结果震源深度只有5、6 km，直接使用编目结果的震源深度做研究工作时不应忽视这个问题。

(4)由于本文中拟合的一维模型都是上行波的数据，因此计算的速度值会比其他模型偏小，而且用拟合曲线的截距作为平均深度仅提供对比意义。

(5)针对震源深度对残差影响的台站分布，我们将在后续工作中进行研究。

范玉兰，林纪曾，胡瑞贺，等.1990.华南地区近震走时表的研制［J］.华南地震，10(2):1－16.

郭永霞，黄媛，张中天，等.2010.华北地区天然地震震相特征研究［J］.中国地震，26(1):112－122.

国家地震局地球物理研究所.1980.震相走时便查表［M］.北京:地震出版社.

滕吉文，张中杰，王光杰，等.2000.地球内部各圈层介质的地震各向异性与地球动力学［J］.地球物理学进展，15(1):1－35.

杨婷，吴建平，房立华，等.2012.华北地区地壳上地幔S波三维速度结构［J］.地球物理学进展，27(2):441－454.

张国民，汪素云，李丽，等.2002.中国大陆地震震源深度及其构造含义［J］.科学通报，47(9)，663 －668.

张慧民，靳平，刘文学，等.2013.基于局部一维模型与走时标定的区域三维速度模型构建技术研究［J］.地震学报，35(2):229－237.

Bouchaala F.，Vavryuk V.，Fischer T..2013.Accuracy of the master-event and double-difference locations:synthetic tests and application to seismicity in West Bohemia，Czech Republic［J］.J.Seis.，17(3):10.1007/s10950－013－9357－4.

Chen Q.，Willemann R.J..2001.Global test of seismic event locations using three-dimensional earth models［J］.Bull.Seismol.Soc.Am.，91(12):1704－1716.

Mahesh P.，Rai S.S.，Sivaram K.，et al.2013.One-dimensional reference velocity model and precise locations of earthquake hypocenters in the Kumaon-Garhwal Himalaya［J］.Bull.Seismol.Soc.Am.，103(2):328－339.

Michelini A.，Lomax A..2004.The effect of velocity structure errors on double-difference earthquake location［J］.Geophys.Res.Lett.，31(9):L09602.doi:10.1029/2004GL019682.

Waldhauser F.，Ellsworth W.L..2000.A double-difference earthquake location algorithm:Method and application to the northern Hayward fault，California［J］.Bull.Seismol.Soc.Am.，90(6):1353 －1368.