直线超声电机精密运动平台系统模型辨识
曹会平,叶 明,姚志远,李晓牛
(1.南京航空航天大学电子信息工程学院,江苏 南京210016;2.南京航空航天大学机械结构力学及控制国家重点实验室,江苏 南京210016)
0 引言
直线超声电机是利用压电陶瓷的逆压电效应、结构的超声振动使其运动,并通过定/动子的摩擦耦合,将结构的微幅振动转换成动子的宏观直线运动[1]。受压电能量转换和摩擦传递等的非线性和分散性影响[2],直线超声电机在运行的过程中表现出较强的时变、非线性和强耦合,故实现其精确定位控制也就变得复杂了。为直线超声电机运动平台建立合理的数学模型,估算某输入条件下电机、平台的输出特性,成为解决超声电机控制的重要手段之一。
近些年,国内外学者在超声电机建模方面做了大量工作[3-8]。大多研究工作集中在超声电机自身的辨识系统上,对超声电机平台的整体辨识研究还比较少;研究对象多为旋转型电机,对直线电机模型辨识的研究也较少。在对电机平台进行研究时,平台除电机外的其他外围设备也会对系统模型产生影响,仅用电机模型代替电机平台进行试验是不准确的。为提高系统模型准确性,对平台进行更加精确的控制,将电机平台作为一个整体进行研究是非常有必要的。
因此,搭建了一个直线超声电机运动平台。建立了直线超声电机运动平台的电压-位移模型。通过比较实际输出与模型输出曲线差异的试验研究,验证了所建系统模型的正确性。为了将平台模型用于定位控制,针对平台模型参数的变化,将各个参数看作是以输入电压为自变量的函数,采用最小二乘法分别对其进行多项式拟合,最后通过实验仿真,得到拟合前后模型输出曲线,从而证明了拟合数据的正确性。
1 直线超声电机运动采集平台
直线超声电机运动采集平台由数据采集设备(包括凌华科技PXI-3910嵌入式控制器和NI PXI-6229数据采集卡)、直线超声电机运动平台和信号调理电路构成。其结构如图1所示。
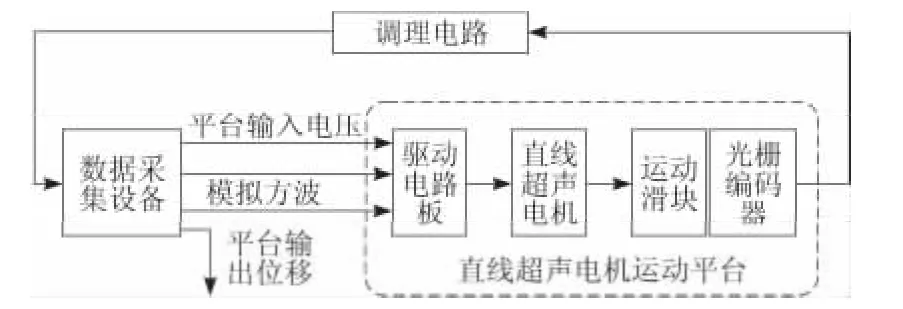
图1 超声电机运动采集平台结构
其中,PXI-3910控制器采用Intel Celeron M 处理器,为位移采集提供了稳固的操作环境,通过人机交互界面实现数据采集卡端口定义、参数设置、数据收发及处理等功能[9]。PXI-6229数据采集卡具有16位量化精度,32路单端A/D模拟输入通道,4路模拟输出通道,2个32位通用计数器,满足平台输入、输出信号端口数目和精度等要求。
直线超声电机运动平台包括直线超声电机驱动板、直线超声电机和装有光栅编码器的运动滑块。驱动电路板产生2路频率可调的正弦信号直接作用于电机,驱动电机运动;后两者构成平台的位移信号生成装置,其实物如图2所示。系统所用的电机是具有连续变截面振子的V形直线超声电机,通过固定盒固定在运动滑块前端。运动滑杆与电机定子无缝接触,其一端连接运动滑块,运动滑块固定在导轨上,只能沿导轨做直线往返运动。在驱动信号作用下,电机定子推动滑杆运动,滑块相应运动,光栅编码器读头发出位移信号。

图2 位移信号生成装置实物
实验中,PXI-6229数据采集卡2路AO口输出方波信号模拟电机驱动板开关,通过改变输出方波的频率以及占空比,控制电机运行时间;1路AO口输出模拟电压,作为平台输入电压信号作用于电机驱动板;1个计数器通道接收调理后的光栅尺信号。当上位机Lab VIEW程序控制数据采集卡输出2路方波开启电机运动时,另一路电压阶跃信号同时输入驱动板,经压控振荡、分频、功率放大和电感匹配后,输出2路相位差为的正弦信号驱动电机运动,电机推动滑块运动,使其上的光栅尺产生A+/A-,B+/B-差分信号,该差分信号再经其后的调理电路转换成A,B 2路单端脉冲信号,数据采集卡采集A,B信号,经上位机处理得到平台运动位移。正弦信号的频率与电压阶跃信号在某一范围内呈线性关系,故改变数据采集卡输出阶跃电压实际上也就是改变电机驱动信号的频率,从而影响电机运动位移。为了实现正弦信号频率微调,该模拟输出电压需要精确到小数点后3位,PXI-6229的16位量化精度完全满足系统需要。
2 实验设计与数据分析
在实验中,运动平台数学模型以输入超声电机驱动板的某一幅值阶跃电压信号为输入信号,在该电压下运动平台运行某一固定时间的输出位移信号为输出信号。由于超声电机响应时间仅为ms级,且实验运动平台总行程为6 cm左右,故实验中选择电机运行时间为200 ms,此时电机运行平稳且运动位移未超平台行程。由于电机谐振频率约为31.9 k Hz,对应的输入电压值为1.508 V,所以输入电压在[1.10 V,1.65 V]范围内时,电机可以正常运行。为了准确研究平台的动态特性,数据采集过程中输入电压信号必须在电机正常运行范围内且覆盖其谐振频率。在电机谐振频率31.9 k Hz左右改变输入电压幅值,采集10组数据点。实验表明,超声电机关断后,负载在10 ms内就会停止运动,位移值稳定不变。因此,考虑采集信号的完整性,电机关断后,使数据采集卡继续连续采集10 ms位移信号,得到平台整个运动过程中的位移数据点。同时,为了减小误差,每个输入电压条件下测量多次位移输出,将位移平均值作为平台位移信号输出。
实验输入的阶跃电压与平台运行位移数据如表1所示。一方面,由于超声电机性能受输入电压影响较大,所以改变输入电压,平台运行位移变化也较大;另一方面,超声电机的非线性决定了在输入电压基本均匀变化的条件下,输出位移变化不稳定。
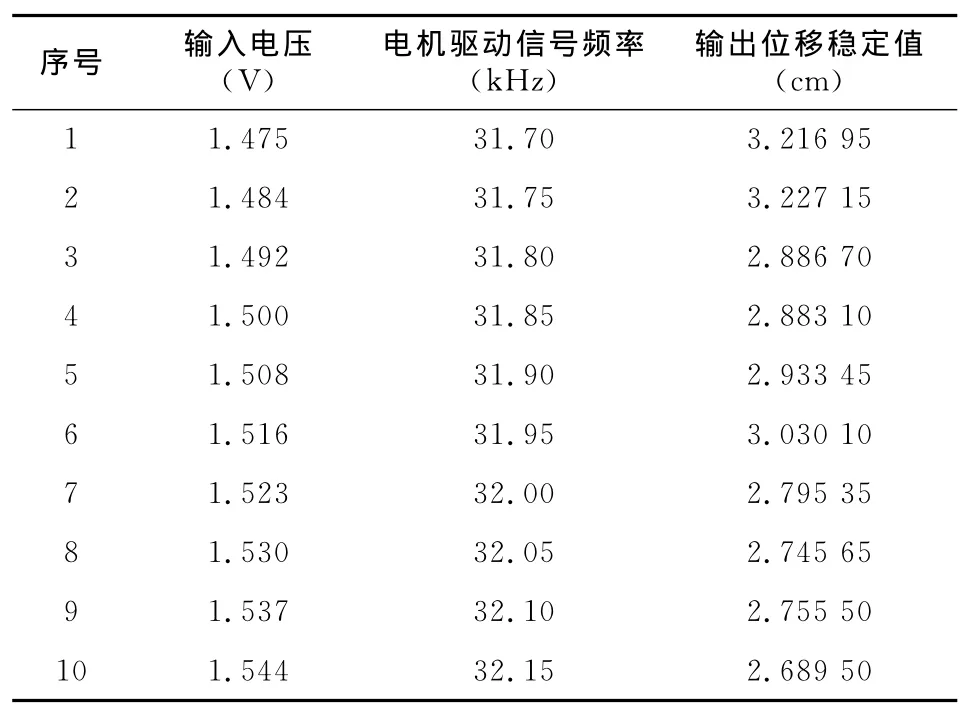
表1 输入阶跃电压与输出位移数据
3 模型辨识
不同输入电压条件下,电机平台阶跃响应曲线为欠阻尼系统,且传递函数的参数会随输入电压变化而变化。为研究方便,简化模型将其看做二阶欠阻尼系统,可设直线超声电机平台传递函数为:
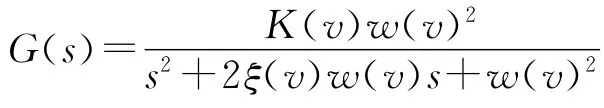
K(v)为放大系数;ξ(v)为二阶系统的阻尼比;w(v)为二阶系统的无阻尼自然振荡频率;v为平台输入电压值。
利用Matlab系统辨识工具箱,分别对表1中10组数据进行模型辨识,建立以电机运动平台电压阶跃信号为输入信号、平台位移信号为输出信号的0零点、2极点的传递函数模型,得到平台模型表达式。模型参数及得到的模型阶跃响应与实际响应匹配度如表2所示。从匹配度来看,系统辨识得到的模型与实际模型较为吻合。
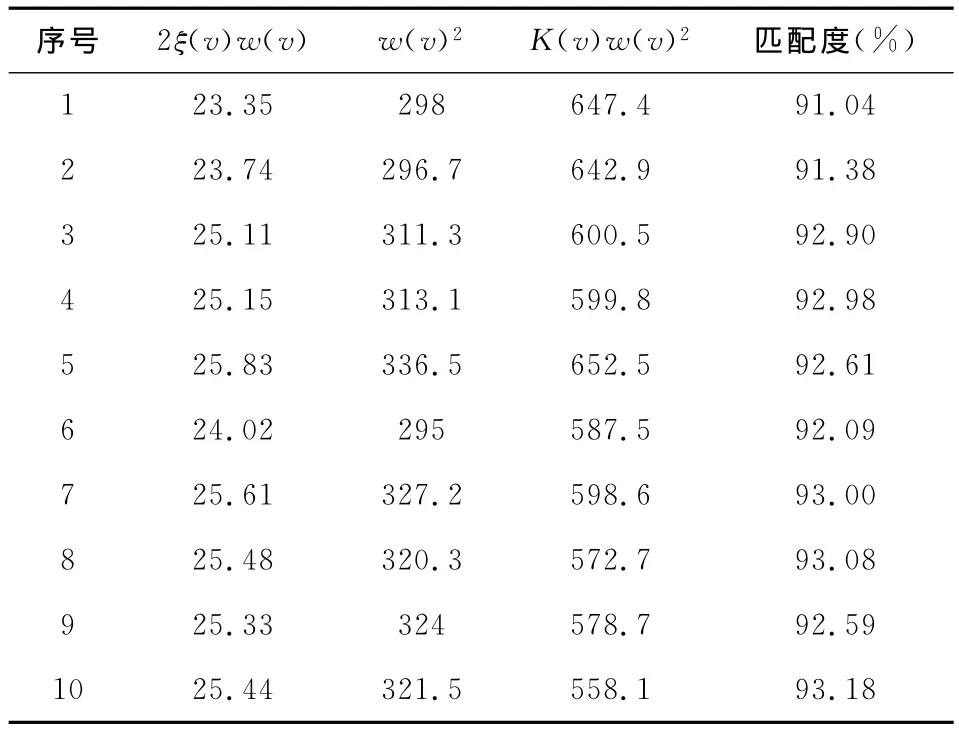
表2 系统辨识模型参数值
以第1组数据为例,将实测位移值与平台模型辨识得到的阶跃响应结果比较,如图3所示。由图3可以看出,系统辨识得到的位移值与实际位移值基本相同。两者之间的误差主要是由于将平台看做二阶系统造成的,随着平台阶数的增加,模型将趋于逼近真实模型。实验表明,当模型取七阶系统时,匹配度接近100%,但七阶系统增加了模型的复杂度,且不利于对平台控制分析。
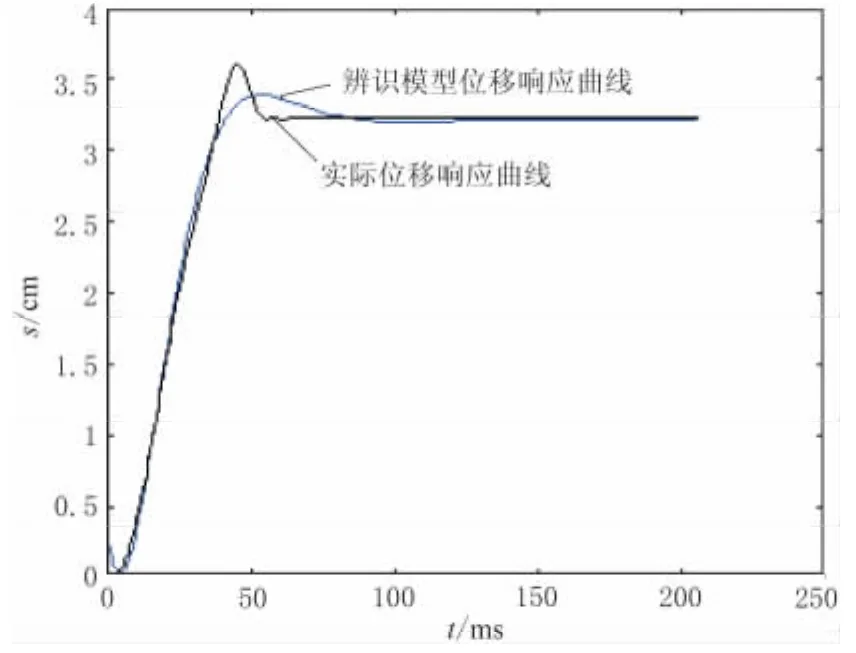
图3 实际位移与平台辨识位移响应曲线
4 参数拟合与拟合模型仿真
由表2也可以看出,得到的模型参数是自变量为输入电压的函数。以最小二乘法为准则,利用Lab VIEW进行二次多项式拟合,并根据拟合多项式,得到拟合后模型参数值如表3所示。
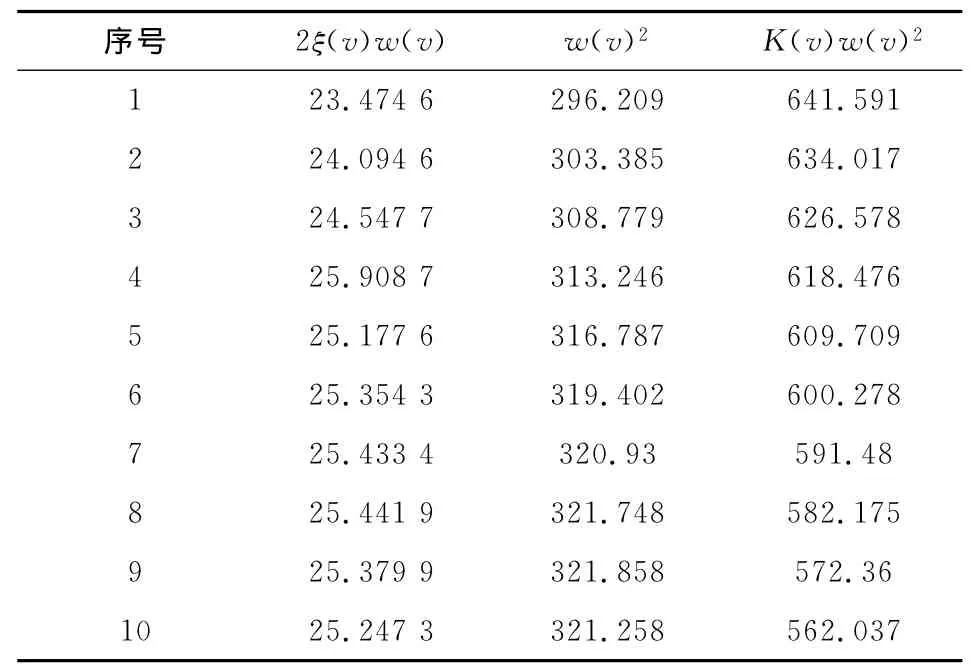
表3 多项式拟合后的参数值
利用Simulink对系统辨识模型进行仿真,得到参数拟合前后的平台阶跃响应曲线如图4所示,其中拟合前阶跃响应用虚线表示,拟合后阶跃响应用实线表示。由2条曲线对比可以看出,拟合结果较理想。
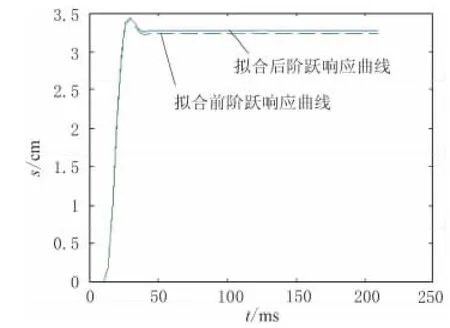
图4 参数拟合前后的平台阶跃响应曲线
5 结束语
将直线超声电机运动平台看做二阶欠阻尼系统,利用Matlab自带系统辨识工具箱,对平台进行辨识得到辨识模型。通过拟合得到以输入电压信号为自变量的模型参数的函数,并对参数拟合后的模型进行仿真。从仿真结果可以看出,利用Matlab系统辨识工具箱,可以灵活、方便地计算得到系统模型,且所得模型与实际模型较吻合。
[1] 陈廉清,任敏杰,张振祥.直线型超声波电机及其应用[J].微电机,2005,38(4):76-78.
[2] 史敬灼.超声波电机运动控制理论与技术[M].北京:科学出版社,2011.
[3] Frangi A,Corigliano A,Binci M,et al.Finite element modeling of a rotating piezoelectric ultrasonic motor[J].Ultrasonics,2005,43(9):747-755.
[4] 刘 博,史敬灼.超声波电机频率-转速控制的阶跃响应建模[J].微电机,2010,43(11):77-80.
[5] 史维佳.超声电机建模及实验研究[D].哈尔滨:哈尔滨工业大学,2011.
[6] 黄青华,魏守水,赵淳生.超声电机的等效电路模型及其参数辨识[J].微电机,2003,36(5):14-16.
[7] 王心坚,金 龙,尧 波,等.行波超声波电机非参数辨识模型[J].中国电机工程学报,2008,28(18):83-89.
[8] 张建桃,张铁民,梁 莉,等.直线超声电机非线性模型辨识[J].华南师范大学学报(自然科学版),2012,44(3):64-67,74.
[9] 张键滔,姚志远,宋小刚,等.基于虚拟仪器的直线超声电机机械特性测试[J].振动、测试与诊断,2012,32(2):218-222.

