最小二乘法在抛光设备压力控制中的应用

孙振杰，王君锋，程启忠

(1.中国电子科技集团公司第四十五研究所, 北京100176；2.华北石油管理局水电厂，河北任丘062552)

在化学机械抛光过程中，压力的变化对化学机械抛光的工艺性有显著的影响，因此晶片在抛光过程中设定精确的压力是非常必要的，如何建立一种行之有效的抛光压力控制方法，是CMP 工艺研究的一个重要方面。

在实际的抛光过程中，压力值的大小不仅影响抛光后晶片表面去除率、粗糙度等工艺指标，而且当压力波动较大时，会对晶片的表面加工质量产生严重的影响甚至产生碎片。因此在抛光设备压力控制部分不仅要考虑控制方法，同时要考虑合理的压力值设定范围。那么如何在蓝宝石晶片抛光过程中，设置合理的压力参数呢，下面采用数值分析的方法进行研究，这里我们主要研究单因子因素，以抛光去除率作为响应变量，抛光压力作为因子，建立响应变量与因子的回归关系。

1 数学描述

在科学实验和统计研究中，往往需要从一组观测值（i=0，1，2，…，n），去寻找y 与x 之间的函数关系，即：y=f(x)。通过最小二乘法拟合曲线的方法，得到y 与x 的拟合曲线。以便直观地研究y随x 的变化关系。

2 最小二乘法拟合曲线概述

求得拟合曲线以后再通过误差分析得到拟合曲线y*(x)对数据(xi，yi)的拟合精度，其中可以用误差平方和σ 来描述：

3 算法分析

由于影响晶片抛光去除率的工艺参数很多，而本方案只考虑抛光压力与抛光去除率的函数关系，因此在实验过程中，保证其它工艺参数设置不变，而逐步增大抛光压力参数设置。通过实验测得抛光去除率与抛光压力关系数据如表1，求抛光去除率y 与压力x 关系的拟合曲线，以便在程序控制中进行压力的校正。

上述的y 一般是在实验中通过观测得到，总会带有观测误差，并且n 往往很大，因此不能要求曲线y=f(x)通过上述数据表示出所有点。

为了得到抛光压力与抛光去除率之间的函数关系，这里我们用最小二乘法分别进行一次、二次和三次多项式的曲线拟合，并通过MINITAB 软件绘制出曲线拟合的图形。

4 程序设计

class pre

{

protected:

int m，n；

double *a，*x，*y；

double dt；

public:

pre(int m，int n)

{

this->m = m；

this->n = n；

dt = 0；

x = new double[m]；

y = new double[m]；

a = new double[n+1]；

}

}

函数中一共有m 个数据点，数据点的x 值，即压力值。

void pre::press()

{

double *vy = new double[m+1]；

double *f = new double[n+1]；

int i，j，k；

double **vx = new double*[n+1]；

double **coe = new double*[n+1]；

for(i = 0；i <= n；i++)

{

vx[i]= new double[m+1]；

coe[i]= new double[n+1]；

/*进行曲线拟合*/

}

for(i = 0；i <= n；i++)

{

for(j = 0；j < m；j++)

{

vx[i][j]= value(x[j]，i)；

}

for(j = 0；j < m；j++)

{

vy[j]= y[j]；

}

}

}

在上述构造的曲线族中寻找一曲线按照某种原则去拟合数据，用所得的拟合数据曲线去代替数据所反应的函数关系。新的拟合曲线记为y*(x)

/*误差分析*/

void pre::deviat()

{

double *funcValue = new double[m]；

double sum=0；

int i，j；

for(j = 0；j < m；j++)

{

funcValue[j]= 0；

for(i = 0；i <= n；i++)

{

funcValue[j]+= a[i]* value(x[j]，i)；

}

sum += (y[j]- funcValue[j]) * (y[j]- funcValue[j])；

}

this->dt = sqrt(sum)；

}

5 结果分析

5.1 病态处理

作曲线拟合，选择基函数是至关重要的，通常要根据具体的物理背景或坐标点（i＝0，1，2，…，m）的分布情况去选择。通常选择幂函数（j＝0，1，2，…，n）作基函数，这时，拟合曲线是n 次多项式曲线。当n 较大（n≥7）时，相应的法方程往往是病态的，n 越大病态越严重，此时需重新选择基函数进行曲线拟合。

本方案中，通过分析可知采用二次和三次多项式拟合所得数据已经满足要求，因此此案例未涉及病态的处理。

5.2 程序运行结果

一次多项式拟合结果：程序运行结果见图1，通过程序运行结果得到的抛光压力（x）与抛光去除率（y）之间一次多项式拟合的函数关系式：

y=0.926458+0.131703 x

均方误差：σ=0.212996

二次多项式拟合结果：程序运行结果见图2，通过程序运行结果得到的抛光压力（x）与抛光去除率（y）之间二次多项式拟合的函数关系式：

图1 一次多项式拟合结果

y=1.1034+0.117686x-0.000935099x2

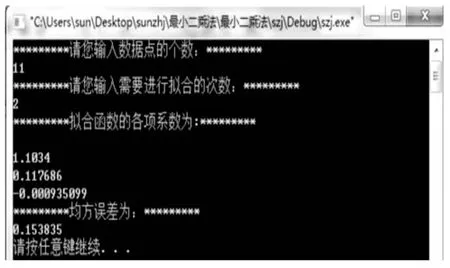
图2 二次多项式拟合结果图1

均方误差：σ=0.153835三次多项式拟合结果：程序运行结果见图3，通过程序运行结果得到的抛光压力（x）与抛光去除率（y）之间三次多项式拟合的函数关系式：

y=0.926458+0.131703x-0.00581965x2-0.00001378x3

均方误差：σ=0.112111

图3 三次多项式拟合结果

5.3 MINITAB 绘制拟合线图

通过图4可以看出，如果抛光压力（x）与抛光去除率（y）之间是一次多项式拟合函数关系时，则实验数据与拟合线图偏差很大，拟合效果不理想，不满足设备工艺参数控制要求。

图4 一次多项式拟合线图

通过图5可以看出，如果抛光压力（x）与抛光去除率（y）之间是二次多项式拟合函数关系时，则实验数据与拟合线图偏差不大，拟合效果相对理想，基本满足设备工艺参数控制要求。

图5 二次多项式拟合线图

通过图6可以看出，如果抛光压力（x）与抛光去除率（y）之间是三次多项式拟合函数关系时，则实验数据与拟合线图偏差很小，拟合效果很理想，满足设备工艺参数控制要求。

通过三次拟合的运行结果以及拟合线图可知，第三次拟合的三次多项式曲线更加贴切的描述出实际问题中出现的抛光压力（x）与抛光去除率（y）之间的函数关系，同时均方误差也在合理值接受范围内。得到的抛光压力（x）与抛光去除率（y）之间三次多项式拟合的函数关系式：

图6 三次多项式拟合线图

y=0.926458+0.131703x-0.00581965x2-0.00001378x3

均方误差：σ=0.112111

该方案完成后，在以后的晶片抛光过程中，可以根据上述函数关系式调整抛光压力工艺参数设置，实现抛光压力柔性连续调节，以达到工艺要求的抛光去除率。

[1]颜庆津.数值分析[M].北京：北京航空航天大学出版社.2012.207-215.

[2]洪楠.MINITAB 统计分析教程[M].北京：电子工业出版社.2007.256-275.