以矢量图为导引的调制解调理论教学方法研究

冯心欣，王新兵，郑海峰，甘小莺，吴炜捷

(1.福州大学物理与信息工程学院，福建福州350116;2.上海交通大学电子信息与电气工程学院，上海210094)

0 引言

“通信原理”课程中的一个重要概念是信号的调制和解调处理，对于该处理的讲解都是必不可少并贯穿始终的。同时，在实际的通信系统中，调制解调处理也是实现信号无线传输和信道复用的基础。因此，将调制解调处理和带通传输系统讲深讲透，有利于学生理解整个“通信原理”的知识体系，为他们后期深入地学习通信领域内的各种新知识奠定良好的基础。

《通信原理》教材[1]和[2]主要从时域波形和频域频谱两个方面对带通传输系统加以分析。这虽然可以全面地描述系统特点，但过多的数学表达式可能会影响学生的理解。本文的重点是讨论如何借助矢量图进行调制解调部分的辅助教学，使得抽象的数学表达式形象化，帮助学生全面深入地理解带通传输系统。

1 矢量图辅助教学思路

我们在“通信原理”课程教学中，引导学生回忆先修课程“信号与系统”中所提到的正交矢量和正交函数的关系，建立“表征信号的一些参数可以与矢量的范数类比，而信号之间的相关性可以利用矢量的内积运算来描述”的概念[3]。接着引导学生建立载波与二维空间正交坐标轴的对应关系。

我们在讲解调制解调系统时，特别是线性调制解调系统的过程中，基于实例引入矢量图法。

2 基于正交函数的矢量图建立

“通信原理”课程通常定义的调制载波为正弦波和余弦波。我们可以帮助学生建立如下概念。

(1)形如cos(ωct)和sin(ωct)的余弦波和正弦波是一对正交函数。其原因在于这两个函数满足如下条件[4]:

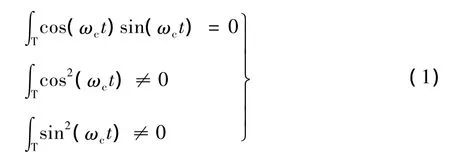
因此，可以把cos(ωct)和sin(ωct)类比成二维空间中的一对正交坐标轴，如x轴和y轴一般。

(2)余弦和正弦函数有如下关系式:

所以可以得出图1所示的矢量图。

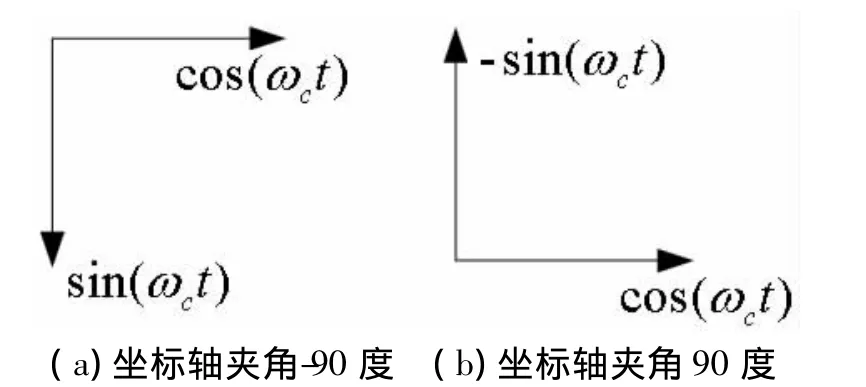
图1 正弦/余弦函数矢量图

该矢量图是正交调制与解调的基础，也是数字调制中信号空间星座图由来的本质[5]。该矢量图适用于包括模拟和数字在内的线性调制解调系统的辅助教学。

3 以矢量图为导引的辅助教学示例

3.1 双边带信号的相干解调

通常“通信原理”课程的教材定义相干解调为:接收端必须提供一个与接收的已调载波严格同步(同频同相)的本地载波(称为相干载波)，它与接收的已调信号相乘后，经低通滤波器取出低频分量。在教学过程中我们发现，通过对时域表达式和频域频谱的分析，学生较容易理解同频的概念，但不易理解同相的概念。我们在此情况下，可以采用矢量图法进行辅助教学，让学生以更直观的方式理解“相干”，为课程后期数字信号的最佳接收部分的讲解打好基础。

我们以教材[1]中的双边带(DSB)信号相干解调处理为例。DSB信号通常可以表示为:Sm(t)=m(t)cos(ωct)。利用相干解调法解调DSB信号时，可以分为两大步骤:①接收信号经过中心频率与调制载频相同的带通滤波器，进行带外噪声滤除;②滤波后的信号与本地载波相乘后经过低通滤波器取出低频分量。

经过步骤①处理的信号可以表示为已调信号和窄带噪声之和，即

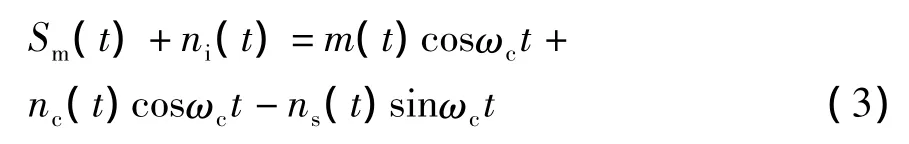
如果以图1(b)为参照坐标系的话，上式可表示为图2所示的矢量图。

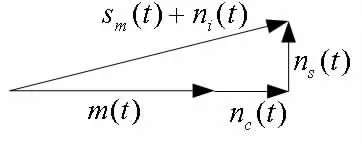
图2 DSB混合信号矢量图

步骤②的处理是真正进行相干解调的过程，类似于将空间中的矢量向坐标轴映射的过程。要解释该概念，需从以下两点入手。

首先，让学生明确以下观点:对于低通滤波器而言，如果输入信号的频率远大于滤波器的截止频率，则低通滤波器等效于积分器。这一观点既可以从直观角度来加以说明，即积分器的输出值是对多个时刻信号输入值的累加，导致信号的抖动被钝化，等同于滤除高频分量;也可以从数学的角度加以说明，即低通滤波器和积分器的传递函数对于频率远大于滤波器截止频率的信号而言是相同的[4，5]。

其次，引导学生理解步骤②的处理过程，即相乘低通处理等价于相乘积分处理也等价于函数间的相关运算，类似于矢量映射。我们观测图2可直观地得出，如果本地载波与已调载波完全同频同相，即生成的是一个“相干”载波，则等价于将Sm(t)+ni(t)映射于cos(ωct)轴，解调出来的信号将由调制信号m(t)和噪声同相分量nc(t)构成，该噪声正交分量ns(t)则完全被消除。反之，如果本地载波与已调载波是同频不同相的，即等价于将Sm(t)+ni(t)映射于cos(ωct+)轴，如图3所示，可能引起信号强度变小和噪声强度变大。在极端情况下，如果本地载波与已调载波正交，即=π/2或-π/2或 ，则等价于将Sm(t)+ni(t)映射于sin(ωct)或-sin(ωct)轴。此时，解调出的信号将完全由噪声正交分量ns(t)构成，不存在任何调制信号分量，解调失败。

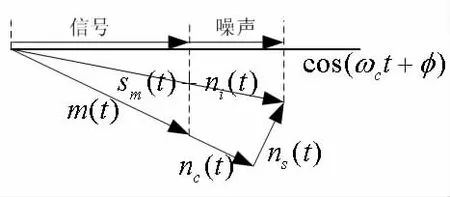
图3 本地载波与调制载波同频不同相

我们可以利用上述矢量图进行辅助教学，帮助学生直观地建立图4所示的思维图，加深对线性调制及相干解调的理解。

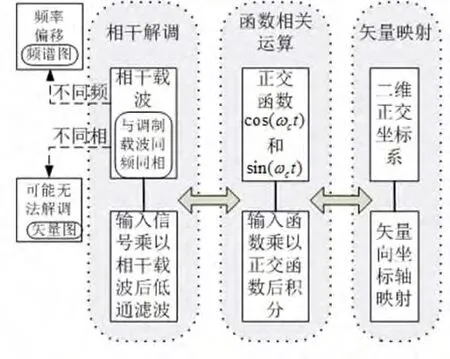
图4 相干解调、相关运算、矢量映射关系图

3.2 调幅信号非相干解调的门限效应

调幅信号可以采用包络检波法进行非相干解调，结合本文3.1节，可以在此处向学生解释“非相干”的含义，即，不需要本地生成相干载波，也没有相乘低通处理的过程。包络检波法的缺点在于存在门限效应，即当包络检波器的输入信噪比小于一定门限值时，解调器的性能将急剧恶化。我们如果以矢量图辅助讲解门限效应，可以降低学生对公式繁杂推导所产生的恐惧心理，同时获得直观的理解，增强教学效果。

同样以教材[1]为例，包络检波器的输入信号可以表示为

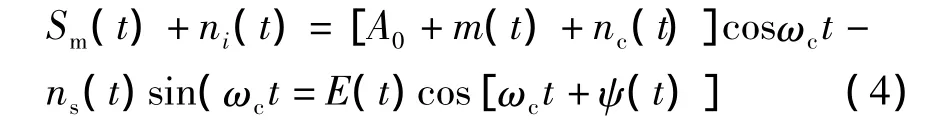
式中，E(t)就是所求的信号与窄带噪声的合成包络，也是包络检波器的输出。在大信噪比和小信噪比的条件下，以图1(b)为参照坐标系，式(4)可以表示成图5所示的矢量图。

图5 AM混合信号矢量图

当包络检波器输入信噪比足够大时，如图5(a)所示，输出包络E(t)近似等于A0+m(t)+nc(t)。该包络中包含有用信号m(t)，此时包络检波器可以正常解调。而当输入信噪比小于某个门限值时，如图5(b)所示，输出的包络E(t)几乎都由噪声构成，包络检波器不能正常解调，出现门限效应。

4 结语

本文提出了基于矢量图的“通信原理”课程辅助教学法。该教学法引导学生建立载波和二维空间正交坐标轴的对应关系，从矢量映射的角度理解调制系统。该方法具有简单直观的优点，可以提高学生对核心知识和概念的理解水平，有助于其后续知识的学习。

[1]樊昌信，曹丽娜，通信原理(第六版)[M].北京:国防工业出版社，2009.

[2]张力军等著，通信原理[M].北京:高等教育出版社，2008.

[3]郑君里，应启珩，杨为理，信号与系统(第三版)(上、下册)[M].北京:高等教育出版社，2011.

[4]Simon Haykin等著，林秩盛等译，信号与系统(第二版)[M].北京:电子工业出版社，2004.

[5]Richard G.Lyons，Understanding Digital Signal Processing(3rd Edition)[M].US:Pearson Education，2010.