基于方向优先和对向搜索的改进Dijkstra算法
唐彩红
(山东万杰医学院,山东 淄博 255213)
0 引言
近年来,随着城市规模的飞速发展和人们生活质量不断提高,交通线路越来越多而复杂,汽车销售量也逐年增加。人们驾车出行时,首要解决的问题是——选择最短的、合适的道路。因此,最短路径问题成为交通网络研究中的一个重要问题。Dijkstra算法是目前最经典、研究最多的一种算法。针对传统Dijkstra算法的不足,许多学者进行了一些研究和改进,如:陆檩等提出了限定区域的搜索方法,姜惠娟则根据顶点的出度和入度对算法进行了优化;还有一些学者在存储结构上做了一些改进:如采用邻接表等,然而,采用这些改进的Dijkstra算法来搜索庞大复杂的交通网络时,占用存储空间大,搜索效率仍然不高[1-8]。为此,本文通过改进存储结构,提出一种基于方向优先和对向搜索的改进Dijkstra算法,以减少存储空间,提高搜索效率。
1 传统Dijkstra算法的弊端
1.1 从搜索方法来分析
传统Dijkstra算法的基本思想是:按照路径长度依次递增的次序生成最短路径。该算法在搜索最短路径时需要逐一遍历网络图中所有顶点,搜索方向具有盲目性,搜索范围很大,从而导致搜索效率很低[9]。求解搜索效率的公式如下:
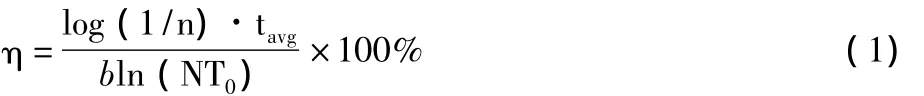
由公式(1)可知,其最短路径搜索效率与需要搜索的顶点数n成反比。显然,随着交通线路和交叉口的增多,采用传统Dijkstra算法搜索最短路径时,搜索效率会大大地降低。根据交通网络的空间特性可知[10-12],从源点到终点的最短路径方向应与源点和终点直接相连的线路方向大致一致,显然,与源点关联的道路的方向与这条线路的方向偏差越小,即方向间的夹角越小,该道路被选中的概率就会越大。因此,本文根据这一原理,提出按方向优先的搜索方法。在搜索过程中,只需从源点的邻接顶点中找出与源点的连线方向和源点与终点的连线方向之间夹角最小的顶点,从而能够避免遍历网络图中与最短路径无关的大量顶点,缩小搜索范围,减少计算量,提高搜索效率。
然而,对于庞大复杂的交通网络,采用按方向优先的单向搜索方法,搜索效率仍然不高。为此,本文提出方向优先+对向搜索相结合的搜索方法。对向搜索是一种能够缩小搜索范围的方法[13]。算法中需设置2个进程,分别从源点和终点同时进行对向搜索,并在搜索过程中都采用按方向优先的搜索方法,从而能够进一步缩小搜索范围(理想情况下搜索范围为原来1/2),加快搜索速度。综上所述,本文提出了方向优先与对向搜索相结合的搜索方法,以提高搜索效率。
1.2 从存储空间来分析
传统Dijkstra算法采用邻接矩阵来存储图的信息。通常情况下,交通网络图对应的邻接矩阵是一个稀疏矩阵,存储了大量的权值为0或∞的无效元素,从而浪费了大量的存储空间,并降低了搜索效率[14]。为此,结合本文提出的搜索方法,采用顶点-弧联合结构来存储图中的信息,其中,弧的信息采用邻接矩阵与判断矩阵联合来存储,顶点信息采用一维数组存储,不仅避免了存储大量无效元素,而且在节省存储空间的同时,还提高了算法的搜索效率。
因此,针对传统Dijkstra算法的不足,提出了一种改进的Dijkstra算法。通过改进存储结构和搜索方法,以加快搜索速度,提高搜索效率。
2 改进的Dijkstra算法描述
2.1 存储结构的定义
首先对交通网络地图进行扫描,然后使用Arc-GIS 9.3 Desktop地理信息系统软件对扫描图进行编辑、处理,提取地图中的路段和路段交叉处,分别将其抽象为图中的弧和顶点,并保留它们之间的拓扑关系,从而生成一个对应于交通网路的带权图G。设图G含有n个顶点、m条弧。结合本文提出的搜索方法,本文采用顶点-弧联合结构来存储图中的信息。
1)顶点的存储结构。
根据方向优先的搜索方法,本文对顶点结构采用一维数组vex[N]来存储,各顶点信息按顶点编号顺序存储,且每个数组元素包括4项。在遍历图中顶点的邻接点时,循环次数可由该顶点的关联弧数h来确定,从而减少无用的循环,大大提高了算法的搜索速度。顶点的存储形式见表1。

表1 顶点的存储形式
2)弧的存储结构。
图中弧的信息采用邻接矩阵与判断矩阵联合来存储。
①构造图的邻接矩阵A。
邻接矩阵A的行数为图G的顶点数,并按顶点编号由小到大排列;列数为网络图中顶点的最大关联弧数(通常交通网中与路口关联的道路不超过4条)。矩阵A中第i行元素的值为与第i个顶点邻接的顶点编号值,并按由小到大排列,如果该顶点的邻接顶点数小于最大关联弧数4,则该行剩下的元素值全置为0。邻接矩阵A占用的存储空间为n×4。
②构造图的关联矩阵B。
关联矩阵B与邻接矩阵A是对应的,其大小与矩阵A相同。将邻接矩阵A各元素的邻接顶点的编号值用与其关联的弧上的权值代替,便得到了邻接矩阵B。邻接矩阵B占用的存储空间也为n×4。
传统Dijkstra算法的空间复杂度为O(n2)。显然,采用本文改进的存储结构,算法的空间复杂度为O(n),节省了大量存储空间,提高了搜索速度。
2.2 方向优先+对向搜索的搜索描述
传统Dijkstra算法在搜索最短路径时需要逐一遍历网络图中所有顶点,搜索范围大,搜索效率低。因此,对传统算法的搜索方法进行改进,提出了方向优先+对向搜索的搜索方法。通过采用方向优先的搜索方法,缩小搜索范围,以避免遍历许多与最短路径无关的顶点,从而提高搜索速度;通过采用对向搜索的搜索方法,能够进一步缩小搜索范围,加快搜索速度。鉴于此,本算法需设置2个进程,分别记作P1、P2,并用集合 U1、U2分别来存放 2个进程搜索到的最短路径上顶点,这些顶点的编号按搜索的顺序分别存放在一个一维数组中。基于2.1节中定义的图的存储结构,方向优先+对向搜索的搜索算法描述如下:
1)2个进程P1和P2分别同时从源点V0和终点V6出发(如图1所示),进行对向搜索。
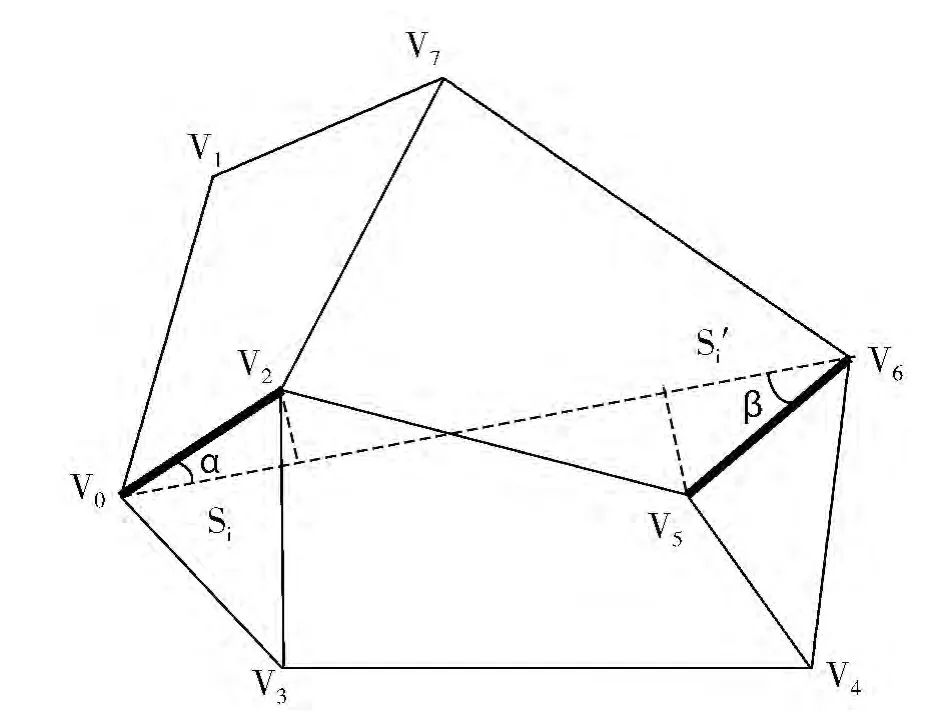
图1 某地区部分交通网络图
现以从源点出发进行搜索的进程P1为例,从邻接矩阵A中依次查找该源点的还未加入到最短路径集合U1中的邻接顶点,并计算该顶点与源点连线方向的斜率、源点与终点连线方向的斜率,进而计算出这2连线方向之间的夹角α。若设待搜顶点、源点和终点的坐标分别为(x,y)、(xc,yc)、(xr,yr),则夹角α的计算公式为:

其中:
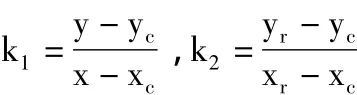
2)按照方向优先的原则,2进程分别选取夹角最小的顶点,并将选取的顶点分别加入到集合U1和U2中。
如图1所示,2进程分别同时从源点V0与终点V6开始对向搜索。进程P1搜索:与源点V0关联的顶点中,V2与V0的连线方向和V0与V6的连线方向之间的夹角最小,应选取顶点V2并将该顶点的信息加入到集合U1中;同理,进程P2选取顶点V5并加入到集合 U2中;U1={V0,V2},U2={V6,V5},如图 1 所示,2粗线弧V0V2和V6V5分别为2进程搜索到的最短路径。
3)现设Si为P1进程进行第i步搜索时搜索到的顶点在直线V0V6上的投影点和源点V0之间的直线长度,Si'为P2进程进行第i步搜索时搜索到的顶点在直线V0V6上的投影点和终点V6之间的直线长度,S为直线V0V6的长度。则:

同理可求得S'i,然后进行如下判断:
①若Si+S'i=S或P1进程在第i步搜索到的顶点恰为P2进程在第i-1步搜索到的顶点且P2进程在第i步搜索到的顶点恰为P1进程在第i-1步搜索到的顶点,则2进程停止对向搜索,并转入步骤4)。
②若Si+S'i<S,则把步骤2)中选取的2顶点分别作为2进程的源点,然后转入步骤1)继续搜索。
③若Si+S'i>S,则说明2进程搜索到最短路径无法汇合,2进程应分别沿着各自的方向继续搜索,即反复执行步骤1)和2),直到2进程搜索到源点或终点,则搜索结束。最后从集合U1和U2中选取最短路径长度较小者作为所求最短路径,并转入步骤5)。
4)将集合U1和U2进行合并,即可得到源点到终点最短路径。
5)搜索算法结束。
按照上面描述的搜索算法,即可求得图2中粗线所示的从源点V0到终点V6最短路径,即V0→V2→V5→V6。
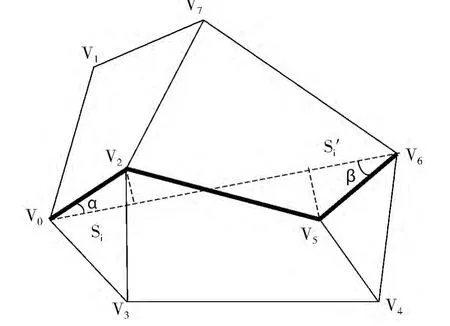
图2 方向优先和对向搜索图
2.3 性能分析
传统Dijkstra算法的空间复杂度为O(n2)。若采用本文改进的存储结构,算法的空间复杂度减少到O(n)。图的存储结构若采用邻接矩阵,搜索各个顶点的邻接顶点时所需时间均为O(n),而采用本文改进的存储结构,搜索时间则减少到O(h)(h为该顶点关联的弧数,h≤4)。基于本文改进的存储结构,采用方向优先的搜索方法,避免了遍历图中与最短路径上无关的大量顶点,算法的时间复杂度大大降低了。若采用方向优先+对向搜索相结合的搜索方法,使算法具有并行化策略,可使算法的时间复杂度在原有基础上进一步降低;当搜索含有较少的顶点和弧的交通网时,采用对向搜索的搜索方法,搜索效率的提高并不明显;但搜索较复杂的交通网时,搜索效率就会明显地提高,最理想情况下可使算法的时间复杂度减少到原来一半,然而最坏的情况下时间复杂度与单向搜索的算法相同。
3 应用实例
为验证改进的Dijkstra算法的性能,实验选取山东省某区域作为研究对象,并设定好出发地和目的地。首先采用ArcGIS 9.3 Desktop软件对该区域进行编辑并抽象成带权图,该图含有75个顶点。分别对改进的Dijkstra算法和传统Dijkstra算法进行模拟搜索最短路径实验,最短路径搜索完毕后,统计出2种算法所遍历搜索的总顶点数,并由此求出2种算法的搜索效率。实验结果如表2所示。

表2 2种算法性能比较表
由表2可看出,若采用传统Dijkstra算法,需搜索的顶点总数为74,计算量大且存储空间大,搜索效率为84.3%;若采用本文提出的改进的Dijkstra算法,存储空间大大减少了,需搜索的顶点数减少到17,搜索效率由84.3%提高到97.2%。由此可见:采用改进的Dijkstra算法,在减少存储空间的同时,加快了搜索速度,提高了搜索效率,表明改进的Dijkstra算法是有效的。
4 结束语
本文针对传统Dijkstra算法的不足,提出了一种基于方向优先和对向搜索的改进Dijkstra算法。通过改进存储结构和搜索方法,节省了大量存储空间,提高了搜索速度。然而,本文提出的改进的Dijkstra算法求解交通网络中的最短路径时,并没有考虑道路的拥塞情况、障碍物存在的情况等,因此还有待于进一步改进,以更好地满足人们的需求。
[1] 陆檩,李世杰,王贵甫,等.港区导航系统中最短路径搜索算法[J].计算机工程,2011,37(17):279-281.
[2] 姜惠娟.Dijkstra最短路径算法的优化及在应急交通中的应用[J].泰山学院学报,2013,35(6):65-68.
[3] 李桂玲.Dijkstra算法的一种改进[J].电脑开发与应用,2009,22(7):13-14.
[4] 徐凤生.最短路径的求解算法[J].计算机应用,2004,24(5):88-89.
[5] 周培德.交通道路网中任意两点之间最短路径的快速算法[J].计算机工程与科学,2002,24(4):35-37.
[6] 肖海俊.最短路径算法在交通导航方面的应用和改进[J].计算机应用与软件,2011,28(9):298-300.
[7] 田昇.基于Dijkstra算法的物流配送系统最短路径程序设计[J].交通标准化,2009(13):89-92.
[8] 黄睿.Dijkstra算法在物流中的优化与实现[J].计算机时代,2012(2):10-12.
[9] 严蔚敏,吴伟民.数据结构(C语言版)[M].北京:清华大学出版社,2002.
[10] 王凌,段江涛,王保保.GIS中最短路径的算法研究与仿真[J].计算机仿真,2005,22(1):117-120.
[11] 李健.基于Dijkstra最短路径算法的优化研究[J].渭南师范学院学报,2009,24(5):61-64.
[12] 王华.基于Dijkstra算法的物流配送最短路径算法研究[J].计算机与数字工程,2011,39(3):48-50.
[13] 郭晶,刘广军,董绪荣,等.嵌入式导航系统的最短路径算法研究[J].装备指挥技术学院学报,2005,16(5):100-103.
[14] 章炯民,窦亮,黄国兴.数据结构与算法教程[M].上海:华东师范大学出版社,2007.
[15] 刘迎春.一种实用的最短路径求解算法[J].浙江工业大学学报,2000,28(2):169-173.
[16] 王志和,凌云.Dijkstra最短路径算法的优化及其实现[J].微计算机信息,2007,23(33):275-277.
[17] 徐涛,郑英,周念.物流最短路径规划最优化计算方法研究[J].物流技术,2013,32(7):236-238.

