基于虚拟目标的KKV逆轨拦截导引方法
舒健生,孟少飞,张士熊
(第二炮兵工程大学906 室,西安 710025)
逆轨拦截是一种特殊的拦截方式,它要求拦截器要在与目标遭遇之前飞到目标正前方的轨道上,并以较小的轨道交角与目标遭遇。这种拦截方式具有较大的拦截概率[1],同时也能提高拦截高速非机动目标的拦截精度[2],但同时也需要已知目标的运动状态信息[3]。考察逆轨拦截的轨道可以看出,逆轨拦截时拦截器的速度方向往往指向卫星轨道的延长方向上,并逐渐向卫星方向转动,在这个过程中,拦截器的位置也逐渐向卫星轨道的延长线靠近,并最终沿着卫星轨道的延长线飞向卫星。因此可以假设存在一个镜像目标T',其飞行方向与真实目标T 相反,并最终与真实目标逆向相遇。而拦截器的飞向过程可以看做是以这个镜像目标为导引的追踪过程,如图1 所示。在这个思路基础上,本文设计了基于组合预测命中点的逆轨拦截导引方法。

图1 虚拟目标示意图
1 虚拟目标的确定
设初始时刻目标在惯性空间的运动参数为RT(t)、VT(t),在较短时间Δt 内,其在惯性空间的运动可以当做“二体问题”来看待。则其Δt 时间后的运动参数可以进行预测

其中K(·)为开普勒方程的解算过程。令Δt = Δt1+ Δt2,则有:

设剩余时间为tgo,由于沿视线方向上的相对速度的变化率较小,因此tgo可用下式进行估计

对式(4)导有

假设预测命中点为m*,其对应的空间位置为R*(t),则R*(t)为目标轨道上的点,且有

其中K1(·)表示取结果的第一项,tgo(t)为t 时刻的剩余时间。经过较小的时间τ 后,预测命中点的位置为

又有
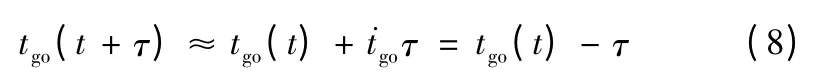
代入式(7)可得

结合式(3)有
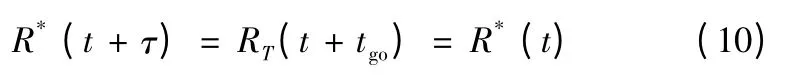
所以m*的移动速度为

记目标在m*点的速度为,则有

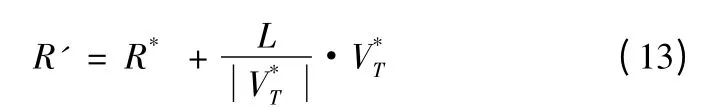
假设T'以恒定的速度向m*靠近,并在tgo时间内到达m*。记其速度为V',则有


将式(14)代入式(15)可得

2 导引方法的选择
考虑到T'运动特点是以恒定的速度和方向向m*运动,并以逆轨的方式与卫星遭遇。如果拦截器能在T'正后方尾随T'飞行,并在tgo时间内追上T'点,则拦截器就能实现对卫星的逆轨拦截。
追踪法是一种控制拦截器的速度方向始终指向目标的导引方法,在视线坐标系下导引律[4]
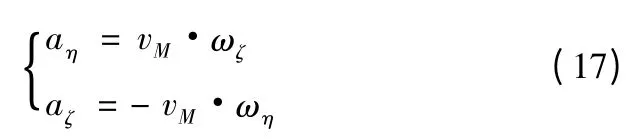
追踪法特点是拦截器在任何起始射角下,都会从目标正后方命中目标。因此,可以用追踪法导引拦截器飞向T',从而实现从正后方命中T',对卫星逆轨拦截的目的[5]。
在飞行过程中,拦截器为了跟踪卫星的运动,其导引头始终是对准目标的。而以T'点作为虚拟目标对拦截器进行导引时,可以假设拦截器有一个虚拟视场是对准T'点的,其与T'点的连线即为虚拟视线LOVS(Light Of Virtual Sight),导引律的解算依赖的是从拦截器到m'点的虚拟视线的信息q'ε、q'β和
当已知T'的位置R'时,拦截器与T'的相对运动状态为
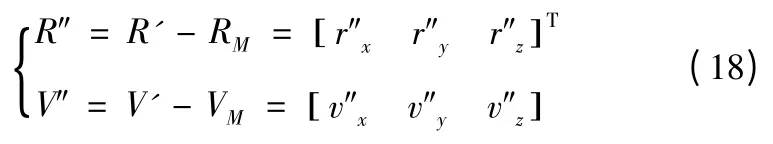
拦截器与T'的距离为
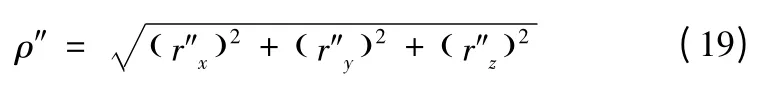
则虚拟视线的高低角和方位角q'ε、q'β分别为
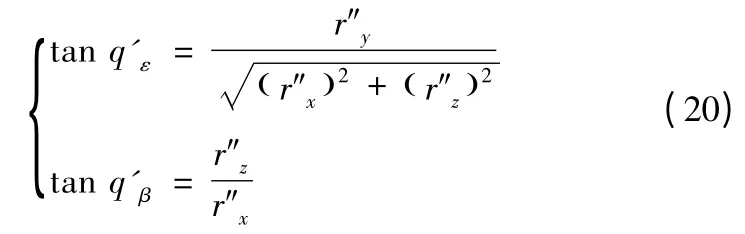
惯性坐标系和由虚拟视线构成的虚拟视线坐标系的转换矩阵为
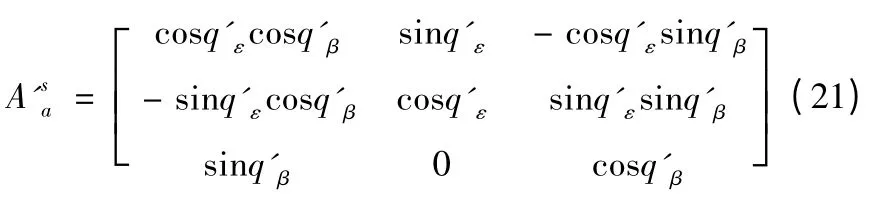
设拦截器和T'点的相对速度转换到虚拟视线坐标系中为V's,则有
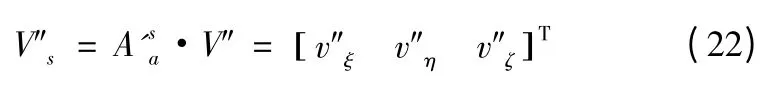
则虚拟视线的转率为

记拦截器的初始速度转化到虚拟视线坐标系中为V'Ms0,则有

由于初始速度往往不是沿着虚拟视线方向的,因此有v'Mη0≠0,v'Mζ0≠0,因此需要在导引律中加入修正项,使v'Mη→0,v'Mζ→0。设计虚拟视线坐标系下的导引律为
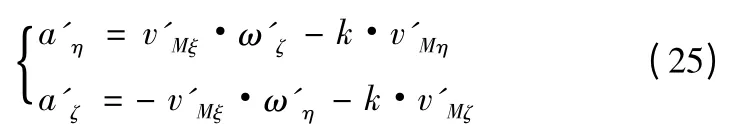
当拦截器和T'点的距离小于一定值时,T'点的误差和移动对视线转率影响增大,此时,拦截器开始以真实目标进行导引。
3 L 取值范围的讨论
追踪法的飞行时间为[6]

其中,ρ'为拦截器和T'点的距离;V'为T'的速度的大小,有V' =;q 为虚拟视线和m'运动轨迹的夹角,即也是虚拟视线和V'的夹角。
为了使拦截器在到达T'的同时,T'也到达m*,需要使T=tgo,同时将式(14)代入式(26)可得方程

式(27)是一个关于L 的超越方程,难以求得解析解。
设拦截器和目标的初始距离为315 km,接近速度为10 km/s,计算不同L 值下F 的值,进而得到F 随L 的变化规律如图2 所示。
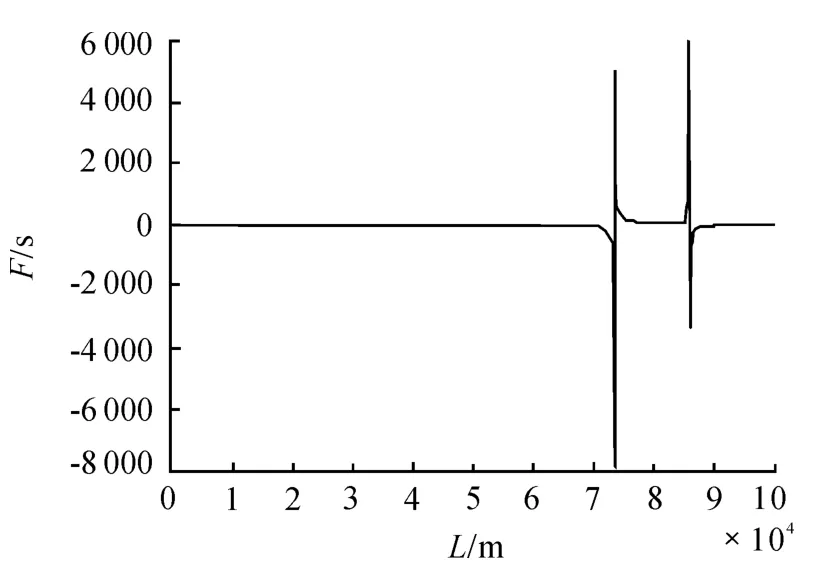
图2 F 随ρ'的变化规律
可以看出,F 并不是随L 单调变化,因此也难以用数值方法求解方程(4.53)。但是从图中可以看出,L≤70 km 时,F 的值基本保持在0 附近,可以近似作为式(27)近似解的范围。
4 推力的转化
加入预测命中点后求得的推力加速度a'η、a'ζ是相对于虚拟视线的法向和侧向的加速度,实际上,拦截器的视线始终是对准真实目标的,其提供的推力加速度也是沿着真实视线的法向和侧向的。因此,需要计算真实视线坐标系中与a'η、a'ζ等效的推力加速度aη、aζ。
考虑到真实视线坐标系中的推力在沿视线方向上为零,但变换到虚拟视线坐标系后沿虚拟视线方向却不再是零,只能保证在虚拟视线的法向和侧向上的分量和计算值相等。因此可以设其沿着虚拟视线的分量为a'ξ,则在虚拟视线坐标系中推力加速度为,其转换到发射惯性坐标系中有

同时,将发射惯性坐标系下的推力加速度转换到真实的视线坐标系中有

联立式(28)和式(29)有

由于qε、qβ和q'ε、q'β都是已知的,因此的值也可以计算得到,在这里将表示为A,即

因此式(30)又可以表示为
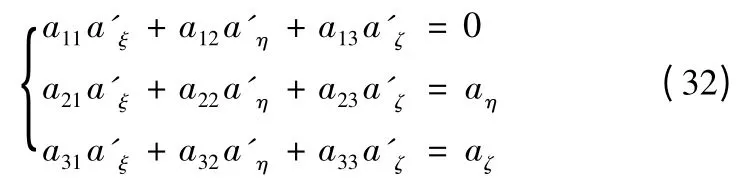
由上式第一项可以解得
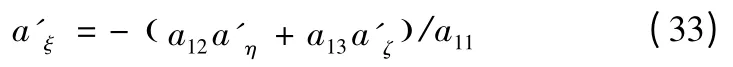
将其代入式(32)后两项则可求得实际视线坐标系下的推力加速度为

5 仿真验证
假设末端初始时刻,拦截器和卫星的初始距离为315 km,接近速度为10 km/s,目标速度为7.036 71 km/s,拦截器速度为3.001 75 km/s。拦截器质量为30 kg,最大轨控加速度为10 g0,取L=20.0 km。
仿真结果显示脱靶量为0.399 536 m,三维效果如图3和图4 所示。

图3 仿真效果图
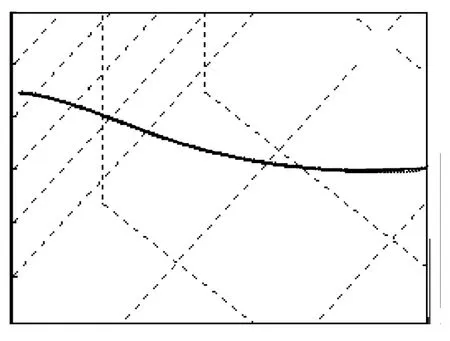
图4 拦截器弹道放大图
由图3 可以看出,拦截器的弹道呈现弧度较小的“S”形,比较平直。由图4 可以看出,拦截器的弹道中间平直,两头有较小的弧度。拦截初始阶段,拦截器向远处的T'飞向,由于距离ρ 较大,虚拟视线转率较小,因此拦截器的速度方向变化较小,弹道比较平直。当接近T'点时,视线转率增大,速度也转动较快,于是在末端附近弹道比较弯曲。视线转率随时间的变化如图5 所示。
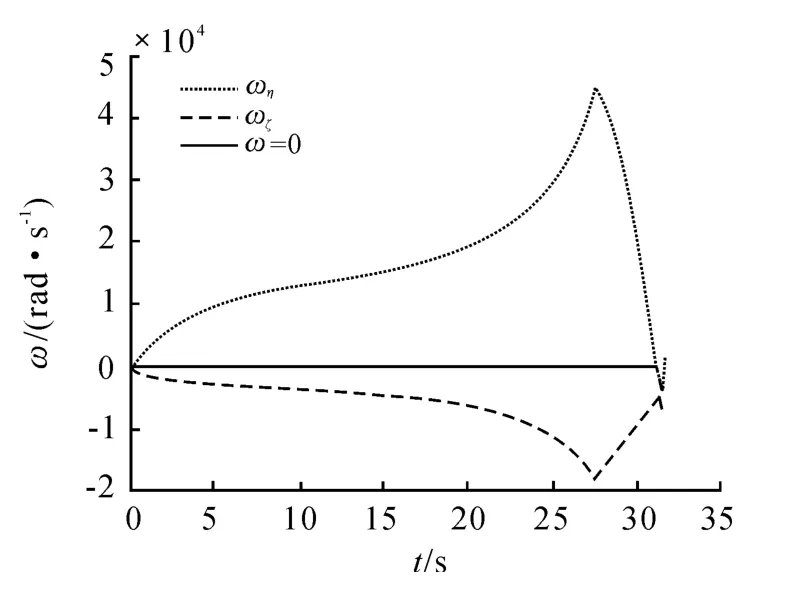
图5 视线转率变化图
由图5 可以看出,视线转率的变化分为两个阶段,第一阶段是拦截器向T'的迅速靠近过程,这个过程中由于ρ 较大,虚拟视线转率小,拦截器的速度方向变化小,视线转率主要由卫星的法向速度决定,并逐渐增大。随着拦截器逐渐靠近T',虚拟视线转率增大,拦截器的速度方向变化较大,抑制了视线的增大,并随着逆轨的逐渐完成,视线转率逐渐减小,并收敛到零附近。最后随着ρ 的减小,视线转率发散。
6 结束语
本文以真实目标运动参数和剩余时间求解出虚拟目标的运动参数,并以低速匀速运动的虚拟目标代替高速变速的真实目标对拦截器进行导引。在导引方法的选择上利用力追踪法总是从目标后方靠近目标的特性,来实现逆轨拦截的目的,并且比较简单与稳定。最后的仿真结果验证了这种方法的可行性,由仿真结果来看,拦截器弹道较为平滑,脱靶量较小。
[1]王继平,鲜勇,王明海,等.轨道交角与时间偏差对拦截卫星拦截概率的影响[J]. 飞行力学,2008,26(5):89-92.
[2]胡小磊.反导逆轨拦截复合制导律研究与仿真[J].空军装备研究,2010,4(1):20-23.
[3]吴鹏.带末段攻击角约束的制导方法研究[D].哈尔滨:哈尔滨工业大学,2009.
[4]雷虎明.导弹制导与控制原理[M].北京:国防工业出版社,2006.
[5]刘兴堂.导弹制导控制与系统仿真[M].西安:西北工业大学出版社,2006.
[6]程国采.战术导弹导引方法[M].北京:国防工业出版社,1996.

