海洋环流模式中的二阶湍流封闭格式综述

梁书秀,严 斌,孙昭晨,张怡辉

(大连理工大学海岸和近海工程国家重点实验室,辽宁大连 116024)

海洋环流模式中的二阶湍流封闭格式综述

梁书秀,严 斌,孙昭晨,张怡辉

(大连理工大学海岸和近海工程国家重点实验室,辽宁大连 116024)

针对目前海洋环流模式预测能力存在的不足,从雷诺应力方程着手,归纳和阐述了二阶湍流闭合模式中压力项、扩散项和耗散项的改进与发展,分析和讨论了各种改进格式对模型完善和预测能力的影响,同时分析了波浪混合作用对环流封闭格式的影响,并对海洋环流模式中二阶湍流封闭格式发展进行了简要综述。压力项的改进主要集中于压力项中各影响量的添加,使得可以模拟的湍流的理查森数Ri趋近1;扩散项的改进主要通过改善湍流能量扩散的第三稳定函数Sk来完成;对于耗散率的改进更多是基于经验,用与理查德森数相联系的阶梯型函数可以有效模拟强分层流;环流模式中通过模拟波浪对垂向扩散系数的影响和在紊动动能方程中考虑波浪破碎耗散的能量的注入,都可以从物理机制上改善目前模式所模拟的混合层太浅和温跃层强度偏低的共性问题。

湍流封闭格式;压力项;扩散项;耗散项;波浪混合

近年来,基于二阶湍流封闭格式假设的地球流体力学研究发展迅速,加之海洋环流封闭模式在海洋表面层的应用日益广泛,海洋环流封闭模式的改进和完善变得越来越重要。海洋环流模式的基本方程为 Navier-Stokes方程。在 19世纪,Navier和Stokes分别以不同的方式对欧拉方程作了修正。1821年,Navier在修正欧拉方程时推导了原始的Navier-Stokes方程,其在推导中没有加入剪切应力的概念,但考虑了分子与分子之间的作用力。Stokes在1845年首次引入动力黏性系数,建立了适合黏性流体的基本方程,即现在流体力学中广泛应用的Navier-Stokes方程。之后,Reynolds[1]建议用统计平均方法来简化Navier-Stokers方程。在Reynolds的统计平均方法中对速度取平均值的时候产生一个问题:由紊动引起的平均量输运项的表达是未知项,使得方程不闭合。对此在1925年Prandtl[2]提出混合长度假设,即把紊动输运项与时均流的当地量建立唯一的联系,以达到封闭二阶未知项的目的。这类在时均流方程中封闭二阶矩的方法称为一阶封闭格式,但只能计算为数不多的几种自相似流。为了弥补这一缺陷,从20世纪40年代开始发展了一批较早的湍流模型,它们放弃了紊动输运项和时均流各量之间较直接的代数联系,转而采用一些紊动量的微分输运方程,如Kolmogorov[3]建议通过求解紊动动能的输运方程来确定其分布。上述模型都是假设湍流的当地状态可用某个速度尺度表征,而且雷诺应力的各个分量均可通过不同的方式与这个速度尺度相联系。为了考虑雷诺应力各分量的不同发展程度,正确地计算复杂水流中各项雷诺应力的输运,有些湍流模型采用雷诺应力的各个分量和紊动热通量的输运方程。在闭合这些二阶矩输运方程中,出现了新的三阶矩,对于三阶矩的处理方法即为二阶封闭格式。

20世纪70年代以后,科研工作者逐步致力于紊动动量方程中各三阶项的改进和发展,如Mellor等[4-6]提出的基本模型,以及在此基础上得到的Level 4、3、2.5和2模型。该类湍流封闭模式MY应用较成熟的是由 Mellor[4]提出的 POM(princeton ocean model)模型,经过多年的改进,已成为较广泛使用的海洋模型。本文将重点总结和概括有关海洋湍流模式已有的研究成果中对动量方程中压力项、扩散项、耗散项的改进和完善,以及相应的优缺点。同时,针对波浪混合及破碎对湍流封闭格式的影响方面的研究做了对比分析。

1 压力相关矩的改进

首先列出二阶封闭过程中所需的动量方程、热通量方程和温度脉动方程的表达式:动量方程

热通量方程

温度脉动方程

式中:i、j、k、m分别表示不同的坐标方向,以区分不同方向的变量及方向导数;ui、uj、uk分别为不同方向的脉动速度;Ui、Uj、Uk分别为不同方向的时均速度;xi、xj、xk分别分别为不同方向的坐标变量;t为时间;ρ为瞬时密度;p为脉动压力;fk为科氏力系数;β为经验系数;θ为温度的紊动变量;gi为重力加速度在i方向的分量;ν为水的运动黏性系数;λ为水的温度分子扩散系数;δik为克罗内克尔符号;Θ为时均温度;εijk为交变符号(当 ijk为123、312、231时,εijk=1;当ijk为213、321、132时,εijk=-1;其他情况下εijk=0)。

公式中带有上划线的量符号表示各紊动变量的时均值。式(1)左侧第1项为时间变化率,第2项为对流输运项;方程右侧第1项为扩散输运项,第2项为压力相关项,第3项为应力产生项,第4项为科氏力项,第5项为浮力项,最后一项为黏性耗散项。式(2)左侧第1项为时间变化率,第2项为对流输运项;右侧第1项表示扩散输运项,第2项和第3项代表时均流场的产生项,第4项为浮力产生项,第5项为压力相关项,第6项为黏性耗散项。式(3)左侧第1项为时间变化率,第2项为对流输运项;右侧第1项表示扩散输运项,第2项代表时均流场的产生项,第3项为黏性耗散项。

Rotta等[5-10]对式 (1)中的压力相关矩进行了相当广泛的研究,压力相关矩一般采用如下简化方式表达:

将压力相关矩表示为压力扩散项和压力应变项(采用∏ij表示),Hanjalic等[11]指出式(4)中右端的前两项(压力扩散项)的量级相对压力应变项较小,可以忽略。较早对∏ij的处理方式是Rotta[5]的能量重分布假设:

式中:l1为经验长度尺度。

式(5)右端第1项表示各脉动速度分量之间的相互作用,第2项表示紊动流动应变率(也可称为平均剪切作用),式(5)的作用即是把能量在各个分量之间重新分配,Mellor等[12-14]也采用此格式。此外,Rodi[8]对压力应变项的模拟就是用压力脉动

泊松方程消去压力应变项中的脉动压力p,从而得出有3种作用对压力应变项有贡献的结论,即各脉动速度分量之间具有相互作用、平均剪切作用以及浮力作用,通常将这3种作用的贡献分别做以下模拟:

式中:K为湍动能;ε为湍动能耗散率;C1、C2、C3、γ和β1均为常数。

由于剪切项和涡量项是各自独立的,所以需考虑涡量效应,而式(6)和式 (7)都没有考虑涡量效应。如果考虑完整性,还应添加非均匀项。Canuto等[15]在湍流模式中考虑了各脉动速度分量之间的相互作用、平均剪切作用、浮力作用、非均匀项以及涡量项,∏ij表达式如下:

其中非均匀项和涡量项分别为

式中α1、α2为常数。式(8)使MY模型中临界理查森数Ricr从0.2提高到1.0。这种变化使大多数模拟出的海洋湍流混合特征能够符合实际情况,这一点已由Martin[16]给予了验证,Martin设置Ricr接近于1.0,在Papa和November两地通过实测得到了正确的混合层深度。此外,Monin[17]的试验数据证明实际理查森数 Ri＞1时湍流交换仍是存在的。图1为普朗特常数随理查森数Ri变化的试验值和计算值对比,Webster[18]的稳定分层流湍流试验测量结果表明混合存在的上限是 Ri接近1.0;Gerz等[19]的直接数值模拟和Wang等[20]的大涡模拟也说明湍流在Ri接近1.0也是存在的。

从图1可以看出,对于压力相关矩的改善主要是考虑更多的压力相关矩的影响因素;从另一方面来说,人们对压力相关矩的了解越来越全面:从最开始的各脉动速度分量之间的相互作用、平均剪切作用、浮力作用,到非均匀项和涡量项影响的添加,使得模型能够模拟越来越大的Ri下强分层湍流,从而对实际海洋混合的模拟也越来越准确。

图1 普朗特常数随理查森数变化的试验值和计算值

2 扩散项的改进

除了压力相关矩的改善之外,如何处理三阶扩散项的研究逐渐受到重视,针对三阶扩散输运项参量化,采用较为广泛的是Mellor等[12]提出来的闭合模式和标准的K-ε模型[21],采用式(9)闭合三阶扩散项:

式中:Sq、Suθ和Sθ为无因次常数;l为湍流基本长度尺度。

式(9)使得方程中三阶扩散输运项降为二阶,封闭了方程组,进而有利于数值求解。此外,Andréj等[22-25]提出了复杂的参量化,但只适用无剪切对流问题。式(9)基于一般假设,只适用剪力项、浮力项和耗散项占主要部分的近似各向同性湍流中,在稳定强分层流中就失效了。这种三阶扩散输运项闭合最常用的方法即是顺梯度逼近 (downgradient approximation,DGA)。虽然DGA能够较好的模拟三阶动量,但Moeng等[26]研究显示DGA低估了三阶动量的值,导致低估了总体动能的垂直通量,因而Canuto等[15]认为应该考虑稳定情况(无时间项),从而将动力方程转换为代数方程(即通用格式),即

式中:u、υ和w分别为x、y和z方向的速度紊动变量;τ为常数;α为膨胀系数;A、B、C、D、E、F、G、H、I和J分别为待定常数。相比于DGA,式(10)使用了二阶动量梯度,虽然能够较准确地模拟三阶动量的值,但是存在大量需要确定的常数,即需要大量的试验数据来确定待定常数,操作起来仍然不方便。此外,对于三阶扩散项的垂直输运项 Fk,Patrick等[27]通过引进湍流能量扩散的第三稳定函数Sk进行参数化,即

图2为湍动能垂向扩散系数的第三稳定函数Sk与理查森数Ri的关系,Sk主要有3种假设。

图2 第三稳定函数Sk与理查森数Ri的关系

a.K-ε模型采用如下关系:

式中:Su为稳定结构系数;σk为扩散常数,取σk=1。

b.Sk常数可由MY模型[12]计算得到:

式中Sk0为经验常数。

c.可由DH模型[11,28]推导得出Sk与湍流动能的垂直分量成正比:

式中:cs为扩散系数;αM、αN分别是关于剪力频率M、浮力频率N的稳定性参数;Sb为稳定结构系数。

由图2可知,K-ε模型的Sk随着Ri减小,直至其为0.85左右,但实际上Ri大于0.85之后,湍流还是存在的,与海洋中的实测数据不符;MY模型采用的是Sk为常数,未能充分反映在低理查森数下Sk实际情况;而DH模型的Sk逐渐减小直至趋近某常数,可以说DH模型综合了K-ε模型和MY模型的优势,充分反映了真实海域下湍流的状态。

应用于海洋和海岸的大多数预测模型的二阶湍流封闭格式的缺陷是:闭合参数只适用于近似各向同性湍流,在湍混合较好和高雷诺数湍流下是满足的,但在强分层流中是不满足的,此时湍流逐渐各向异性,这一点可由 Yamazaki[28]的海洋实测、Thoroddson等[29]的试验数据和Itsweire等[30]的直接数值模拟所证明。

由上述分析可知,DH模型虽然仍旧采用DGA的格式,但它将Sk与Ri之间建立起一个可以反映实际湍流垂向特性的联系,即在高Ri下,湍流也是能够模拟的,这大大增加了湍流的模拟区域,同时减弱了低估三阶动量值的可能性。

3 耗散项的改进

对于动量方程中的耗散项,采用无因次变量法得到经典公式如下:

式中Λ为湍流特征长度尺度。对于热通量和温差方程中的耗散项,由Mellor的早期模型[12]可得

其中

式中l2、Λ2为与温度相关的长度尺度,可由湍流主长度尺度乘以一个常量得到,而常量的值需要由试验得到。

式(17)的初处理方式如同式 (16),但是式(16)没有进行二次处理,而式(17)和式(18)进行了二次处理。式(17)是将uiθ的平均值与温度对流项、浮力项和科氏力项相联系,而 式(18)只是与温度对流项相联系,相对而言,式(18)处理更简单。

在Dickey[31]的分层流试验(下文称为DM试验)中,湍流逐渐衰减直至临界理查森数,湍流的涡动转化成线性内波。而根据DM试验,由分子黏性引起微小的衰减仍然存在,而且随着雷诺数增大而减小。鉴于此,Mellor[32]对MY模型进行了修正,用与理查德森数相联系的耗散率代替已有的子模型耗散,同时为了模拟分层流和耗散率的中断,对ε进行如下处理:

式中:H(Rq)为与理查森数相关的阶梯函数;N为浮力频率;Rqc为Rq的临界值,约等于100。

渤海的实测数据显示湍耗散率在垂直结构存在间断性的分布,如图3所示,其中χθ为热耗散率。t4测点在水深10 m处湍耗散率变化有3个数量级,而式(19)(20)可以有效地模拟耗散率的中断。

但当MY模型在整个海洋上表边界层运用时,在夏季稳定分层情况下,会出现过浅的海洋表面层深度和过高的海表温度现象。鉴于此,Kantha等[14]认为有必要修改MY模型,而且直接在混合层中添加涡黏系数和扩散系数(即放弃了经验常数是无因次变量的原则)。此外,Martin[16]在 Papa和November两个站点的实测结果也说明MY模型中过浅的混合层导致夏天海表温度过高这一事实,MY模型中夏季海表温度仍然是偏高的,因此仍然需要改善。

为了和原来的MY模型相应的项表达一致, Mellor[32]对变量进行了变换,设Rq=-B21GH,其中B1为常数,则式(19)(21)分别可以变为式(22)(23)。

式中GHc为需要指定的常数,一般可以通过模拟值和实测值的符合良好时给定。

Mellor证明了涵盖并依赖理查森数的耗散率能增加分层外围部分的湍流动能,增加了边界层的厚度,而且能够改善与风压和热通量实测结果的吻合程度[16]。当然有些因素使得模型计算与实测数据吻合不是很理想,除了模型物理量的过度简化和实测数据误差,还包括未知内波、表面波等原因。

对于耗散率的模拟,用与理查德森数相联系的阶段性函数有效模拟强分层流(各向异性湍流),这说明了未涵盖、未依赖理查森数的耗散率低估了湍流的动能,未能有效捕捉到湍动能;这也证明了耗散率也是依赖于理查森数的,进一步说明了强分层流的本质。

图3 渤海各测点湍耗散率和热耗散率垂向分布

4 波浪对湍流封闭格式的影响

波浪在海洋和大气的能量、动量及气体交换中起着重要作用。波浪引起的海洋上层湍混作用通常认为有3种机制[33]:波浪破碎产生的紊动和混合;波流相互作用产生的Langmuir环流;非破碎波浪水质点运动水平速度的垂直梯度产生的剪切流对紊动产生的贡献。

海洋环流控制方程中的雷诺应力项可以直接体现海洋的混合过程,该项依据不同的参数化方法来闭合方程组,是海洋环流数值模式研究中最薄弱的环节[34]。Qiao等[35]建立了波浪运动混合的理论框架,基于该理论并利用海浪数值模式,可以得到实时的三维波致雷诺应力和波浪运动对环流场的混合作用。

其中,波浪破碎的湍混作用一直是个难点。由波浪破碎引起的湍混作用的经典描述来源于Craig等[36]模型。其中波浪破碎对紊动的贡献是通过在紊动动能方程中添加通量,该通量来源于波能的耗散。Rascle等[33]等综合了以前的研究,给出了以下的表达方式:

式中:Sm和Sq是模型参数,分别取0.39和0.2[12];τw为由波浪运动引起的垂向动量的通量;DE(c)表示在相速度c到c+dc范围的破碎波的能量损失;fc(z)为标准化深度函数,表示每一个破碎波的能量注入深度,这里正比于破碎波的波长。

整个紊动动能能量注入的剖面取决于fc(z)和DE(c)参数化方法选择。Craig等[36]模型和观测中耗散率的对比使得Craig等[36-40]认为有更大的近表面扩散,否则湍动能就难以穿越到很深的水域。在波浪破碎下,剪切产生项和耗散项不再守恒。相比于Craig等[36]模型,Kudryavtsev等[41]认为波浪破碎引起的湍流是湍动能和湍动量直接注入到某一深度,并且此深度与波高是同一个量级,他将 fc(z)和DE(c)分别采用如下格式:

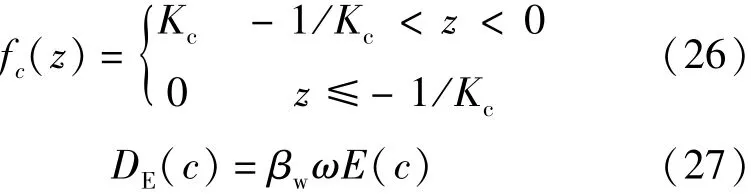
式中:Kc为波数;βw为风成波成长率;ω为辐散频率; E(c)为能量谱函数。Kudryavtsev选择了一个较简单的饱和谱,在谱峰处高速截断,βw可采用如下公式:

式中:cβ是常数;u*为空气与海面的摩阻流速。

Kudryavtsev的方法考虑了波浪破碎的行为,例如微尺度的破碎,并且纳入到模型的亚黏层中。因为波浪破碎在水面下能产生较长久的湍流,而这种波浪破碎与微尺度的破碎有关的。Kudryavtsev的描述符合耗散率的观测结果,也符合表面的“cold skin”和亚黏性层的观测结果。这一点可以由Terray等[37]基于试验结果提出的3层结构得到证明,试验结果表明水体上层(水深为波高的60%)是由波浪破碎引起的湍流注入区,并同时有50%的能量耗散。而其之下的变化层(耗散正比于z-2),与更深层(壁面相似定律适用)是可以合并考虑的。Kudryavtsev的这种描述摆脱了Craig等[36]模型中海表面的粗糙尺度,仅仅基于破碎波的大小和谱分布。

另一种波浪破碎能量注入到一定深度的方法体现在Sullivan等[42-43]复杂的模型中。这些模型采用直接数值模拟或是大涡模拟的破碎波浪的分布来解决动量在某一深度注入。假设波浪破碎是随机的:①波浪破碎是一个在时间和空间上均匀分布的随机过程;②用空间和时间上的紧致函数代替单体波浪破碎,以便从破碎波浪中捕捉到平均体脉冲,这样可以避免空气-水完全模拟的复杂性;③强迫破碎脉冲是互相不影响的,使得在波浪破碎区可以由离散的事件叠加而成。

对于Pwb(z),Sullivan等[42]采用类似于Kudryavtsev的格式:

式中b2是依赖于波龄的常数,并由对海洋通量的总能量和总动量决定。

由式(26)(27)(29)(30)对比分析,可知Sullivan模型中的fc(z)更浅,因而耗散率相对更小,同时Sullivan模型中的这种分布,只有少量能量是通过波浪破碎耗散的。尽管Sullivan选择的破碎波浪的分布在物理上是合理的,即当波浪成长时,波浪破碎向高频移动,但与实际观测的耗散率吻合较差。这种结果来源于过小的波浪破碎注入深度和波浪谱分布的格式选择,故而有只有短波导致耗散。此外, Sullivan的分析得出:未充分发展的波浪比成熟波浪的湍流注入更大的深度,这与Terray等[37]所测结果相反。

5 结 语

对于海洋环流模式中二阶湍流闭合模式的各项模拟,学者们更倾向于不断完善各项与理查森数的关系,使之能够反应强分层流的本质,并且取得了较好的成果。但环流模型中现有的模式普遍低估了各种动力条件对海表的混合作用,同时缺乏海表强风、波浪对环流作用的实测及模型化研究,例如如何有效地定义风能的输入方式,风能输入(特别是强风作用下)在波浪不同成长阶段的作用如何等,这些机理性的问题在海洋观测、试验研究和数值模拟方面的结论还存在一定的差异,不同研究的结论有时甚至是相悖的。而对于这个在海洋环流和表面混合中起着重要作用的波浪破碎动力过程的研究,由于波浪破碎模型发展的瓶颈和对该过程能量、动量、气体交换机理性研究的欠缺和困难,还有很多工作需要进一步的深入展开,从而不断完善海洋环流模式的诊断和预测能力。

[1]REYNOLDS O.On the dynamical theory of incompressible viscous fluids and the determination of the criterion[J].Philosophical Transactions of the Royal Society of London. 1895:123-164.

[2]PRANDTL L. Bericht über untersuchungen zur ausgebildeten turbulenz[J].Z Angew Math Mech,1925, 5:136-139.

[3]KOLMOGOROV A N.The local structure of turbulence in incompressible viscousfluid forverylargeReynolds numbers[J].Mathematical and Physical Sciences,1991, 434:9-13

[4]MELLOR G L.Analytic prediction of the properties of stratified planetary surface layers[J].Journal of the Atmospheric Sciences,1973,30(6):1061-1069.

[5]ROTTA J C.Statistiche theorie nichthomogener turbulenz [J].Zeitschrift für Physik,1951,129(6):547-572.

[6]LUMLEY J L,KHAJEH-NOURI B.Modeling homogeneous deformation of turbulence[J].Advances in Geophysics, 1974,18A:162-192.

[7]LAUNDER B E,REECE G J,RODI W.Progress in the development of a reynolds-stress turbulence closure[J]. Journal of Fluid Mechanics,1975,68(3):537-566.

[8]RODI W.A new algebraic relation for calculating the Reynolds stresses[J].Z Angew Math Mech,1976,56: 219-221.

[9]SHIH T S,SHABBIR A.Studies in turbulence[M].New York:Springer-Verlag,1992.

[10]GATSKI T B,SARKAR S,SPEZIABLE C G.Studies in turbulence[M].New York:Springer-Verlag,1992.

[11]HANJALIC K,LAUNDER B E.A Reynolds stress model of turbulence and its application to thin shear flows[J]. Journal of Fluid Mechanics,1972,52(4):609-638.

[12]MELLOR G L,YAMADA T.Development of a turbulence closure model for geophysical fluid problems[J].Review of Geophysics and Space Physics,1982,20(4):851-875.

[13]MELLOR G L.Retrospect on oceanic boundary layer modeling and second moment closure[C]//MüLLER P, HENDERSON D.Parameterization of small scale processes.Hawaiian:Winter Workshop,1989:251-272.

[14]KANTHA L,CLAYSON C A.An improved mixed layer modelforgeophysicalapplication [J].Journalof Geophysical Research,1994,99(C12):25235-25266.

[15]CANUTO V M,HOWARD A,CHENG Y,et al.Ocean turbulence,part I:one-point closure model momentum and heatverticaldiffusivities [J].JournalofPhysical Oceanography,2001,31(6):2546-2559.

[16]MARTIN P J.Simulation of the mixed layer at OWS November and Papa with several models[J].Journal of Geophysical Research,1985,90(C1):903-916.

[17]MONIN A S,YAGLOM A M.Statistical fluid mechanics: mechanics of turbulence[M].Cambridge:The MIT Press, 1971.

[18]WEBSTER C A G.An experimental study of turbulence in a density stratified shear flow [J].Journal of Fluid Mechanics,1964,19(2):221-245.

[19]GERZ T,SCHUMANN U,ELGHOBASHI S E.Direct numericalsimulation stratified homogeneousturbulent shear flows[J].Journal of Fluid Mechanics,1989,220 (1):563-594.

[20]WANG D,LARGE W G,MCWILLIAMS J C.Large eddy simulation of the equatorial ocean boundary layer:diurnal cycle,eddy viscosity and horizontal rotation[J].Journal of Geophysical Research,1996,101(C2):3649-3662.

[21]RODI W.Turbulence models and their application in hydraulics[M].Delft:IAHR Publication,1984.

[22]ANDRÉJ C,LACARRÈRE P.Mean and turbulent structures of oceanic surface layer as determined from onedimensional,third-ordersimulations[J].Journalof Physical Oceanography,1985,15(2):121-132.

[23]CANUTO V M.Large eddy simulation of turbulence:a sub-grid model including shear,vorticity,rotation and buoyancy[J].The Astrophysical Journal,1994,428(2): 729-752.

[24]ABDELLLA K,MCFARLANE N.A new second-order turbulence closure scheme for the planetary boundary[J]. Journal of the Atmospheric Sciences,1997,54(14):1850-1867.

[25]ZILITINKEVICH S,GRYANIK V M,LYKOSSOV V N,et al.Third-order transport and nonlocal turbulence closures for convective boundary layers[J].Journal ofthe Atmospheric Sciences,1999,56(19):3463-3477.

[26]MOENG C H,WYNGAARD J C.Evaluation of turbulent transport and dissipation closures in second-order modeling [J].Journal of the Atmospheric Sciences,1989,46(14): 2311-2330.

[27]PATRICK J L,SANDRO C,GEORG U.Validation of turbulence closure parameterizations for stably stratified flows using the PROVESS turbulence measurements in north sea[J].Journal of Sea Research,2002,47(3): 239-267.

[28]YAMAZAKIH.Stratified turbulence neara critical dissipation rate[J].Journal of Physical Oceanography, 1990,20(10):1583-1598.

[29]THORODDSON S T,VAN ATTA C W.The influence of stable stratification on small-scale anisotropy and dissipation in turbulence[J].Journal of Geophysical Research,1992,97(C3):3647-3658.

[30]ITSWEIRE E C,KOSEFF J R,BRIGGGS D A,et al. Turbulence in stratified shear flows: implications for interpreting shear-induced mixing in the ocean[J]. Journal of Physical Oceanography,1993,23(7):1508-1522.

[31]DICKEY T D.An experiment study of decaying and diffusing turbulence in neutral and stratified fluids[D]. Princeton:Princeton University,1977.

[32]MELLOR G L.One-dimensional,ocean surface layer modeling:a problem and a solution[J].Journal of Physical Oceanography,2001,31(3):790-809.

[33]RASCLE N,CHAPPON B,ARDHUIN F,et al.A note on the direct injection of turbulence by breaking waves[J]. Ocean Modelling,2013,70:145-151.

[34]张敬.海岸、河口区三维近岸环流与物质输运数值研究[D].青岛:中国海洋大学,2010.

[35]QIAO F,YUAN Y,YANG Y,et al.Wave-induced mixing in the upper ocean:distribution and application to a global ocean circulation model[J].GeophysicalResearch Letters,2004,31(11):L11303.1-L11303.4.

[36]CRAIG P D,BANNER M L.Modeling wave-enhanced turbulence in the ocean surface layer[J].Journal of Physical Oceanography,1996,26(5):2546-2559.

[37]TERRAY E A,DONELAN M A,Agrawal Y C,et al. Estimates of kinetic energy dissipation under breaking waves[J].Journal of Physical Oceanography,1996,26 (5):792-807.

[38]TERRAY E A,DRENNAN W M,DONELAN M A.The vertical structure of shear and dissipation in the ocean surface layer [C]//Csanady G T.Proceeding of symposium on air-sea interaction.Sydney:University of New South Wales,2000:239-245.

[39]SOLOVIEV A,LUKAS R.Observation of wave-enhanced turbulence in the near surface layer of the ocean during TOGA COARE[J].Deep Sea Research,2003,50(3): 371-395.

[40]GEMMRICH J R,FARMER D M.Near-surface turbulence in the presence of breaking waves[J].Journal of Physical Oceanography,2004,34(5):1067-1086.

[41]KUDRYAVTSEV V,SHRIRA V,DULOV V,et al.On the vertical structure of wind-driven sea currents[J].Journal of Physical Oceanography,2008,38(10):2121-2144.

[42]SULLIVAN P P,MCWILLIAMS J C,MELVILLE W K. The oceanic boundary layer driven by wave breaking with stochastic variability,part 1:Direct numerical simulation [J].Journal of Fluid Mechanics,2004,507:143-174.

[43]SULLIVAN P P,MCWILLIAMS J C,MELVILLE W K. Surface gravity wave effects in the oceanic boundary layer: large-eddy simulation with vortex force and stochastic breakers[J].Journal of Fluid Mechanics,2007,593:405-452.

Review of two-order turbulence closure schemes for ocean circulation model//

LIANG Shuxiu,YAN Bin,SUN Zhaochen, ZHANG Yihui
(State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024, China)

A brief review of the development of second-order turbulence closure is presented aiming to overcome the two deficiencies in the prediction of the ocean circulation model.The paper begins from Reynolds stress equations,analyzes and summarizes the improvement and development of pressure relations term,diffusions term,and dissipations term aiming at stating the effects of the terms on the prediction ability of corresponding turbulence closure.Finally,the different ways to consider the wave mixing in ocean circulation model are discussed as well.The improvement of pressure correlation focuses on adding the relative terms such that the Richardson's number of the turbulence approaches 1.The diffusion term is improved by the third stability function Sk.The improvement of dissipation relies on the empiricism by using the Heaviside step function to simulate the strong stable stratified flow.In simulating the wave impact on the vertical diffusion coefficient and injecting energy dissipated in wave breaking into turbulent kinetic energy equation,the two general problems-too shallow mixing layer and the low intensity of the thermocline-may be improved physically.

second-order turbulence closure;pressure relations;diffusions;dissipations;wave mixing

TV131.2;P751

:A

:1006-7647(2014)04-0082-07

10.3880/j.issn.1006-7647.2014.04.018

2013-0704 编辑:周红梅)

国家自然科学基金(51279028)

梁书秀(1972—),女,辽宁凤城人,副教授,博士,主要从事海洋环境数值模拟及海洋信息数字化研究。E-mail:sxliang@dlut.