岩体间超低摩擦发生机理的摆型波理论

潘一山 王凯兴

（辽宁工程技术大学力学与工程学院，阜新 123000）

岩体间超低摩擦发生机理的摆型波理论

潘一山 王凯兴

（辽宁工程技术大学力学与工程学院，阜新 123000）

针对深部冲击地压发生时煤岩体有明显的错动现象，基于块系岩体中的摆型波传播理论，研究摆型波在块系岩体中传播时诱发岩块间的超低摩擦发生机理。通过分析动力作用下岩块间的相对位移最大值，研究块系岩体的超低摩擦发生规律。当岩块间的软弱介质处于拉伸最大值状态时，在侧向扰动作用下岩体极易发生超低摩擦滑动，由此给出了块系岩体的超低摩擦发生判据。最后，通过计算分析了块系岩体自身特性及外界扰动特性对岩块间超低摩擦的影响。基于摆型波理论的超低摩擦发生机理研究，对认识深部岩体错动型冲击地压启动规律具有重要意义。

岩石力学 块系岩体 摆型波 超低摩擦

0 引言

在煤炭深部开采过程中冲击地压动力灾害将更加剧烈和频繁。深部煤岩体在高应力状态下的采动过程中诱发冲击地压能使煤层错动1m多，这种现象在高应力状态下难以解释，极有可能是煤岩体间的摩擦力减弱而诱发的。同时，深部煤岩体的真实存在状态应是具有不同等级的块系结构，块体间摩擦力的变化对煤岩体的结构稳定具有重要影响。在动力作用下块体的运动与块体间的摩擦有密切的关系。岩体间超低摩擦的研究，将对认识深部岩体错动型冲击地压启动规律具有重要意义。Kurlenya等（1999）在对深部块系岩体动力传播研究中发现了岩体的不规则超低摩擦现象并进行了相关实验研究。钱七虎（2004）、王明洋等（2005）分别对深部块系岩体的静力和动力问题中的超低摩擦进行了理论和实验分析。吴昊等（2008）分析了块系岩体中的超低摩擦现象。姚路等（2013）通过实验研究了高速滑动条件下，岩石的摩擦系数会随位移大幅降低。块系岩体的超低摩擦与摆型波动力传播的内在机理联系有待于进一步研究。因此，我们基于块系岩体中的摆型波传播理论来研究岩体中的超低摩擦现象。针对Sadovsky（1979）提出的深部岩体等级块系构造理论，目前Aleksandrova等（2004，2006，2008）、潘一山等（2012）分别对块系岩体中的摆型波动力学传播过程进行了相关研究，为研究块系岩体中的动力传播诱发岩体间的超低摩擦提供了理论基础。

摆型波在块系岩体中传播时，岩块间的软弱连接介质在块体的作用下呈现周期的拉伸和挤压变化。当相邻岩块间的软弱介质在拉伸方向上的相对位移达到最大值时，相邻块体呈现出最大的“剥离”状态，岩块间的正压力相对较小，若在侧向力作用下容易造成块体间的超低摩擦滑移。因此，基于摆型波传播动力模型，研究在外界扰动作用下块系岩体动力响应过程中岩块间相对位移的动态变化。通过岩块间的最大“剥离”即沿传播方向上相邻岩块间相对位移在拉伸方向上的最大值，给出超低摩擦发生准则。同时指出块系岩体中的动力传播还存在岩块间的“超强挤压”现象。

1 冲击扰动下块系岩体动力模型

依据Sadovsky（1979）提出的深部岩体等级块系构造理论，在块系岩体中的动力传播，会产生一种特殊的岩体动力响应现象——摆型波。Kurlenya等（1993，1996）发现了岩体受爆炸作用产生了信号交错变化的现象，据此用爆炸的方法在岩体内部形成空隙时，在岩块的周围发生块间不同符号的位移相互对应的摆动。这一现象的发现使得基于连续介质力学的弹塑性应力波理论难以给出合理的解释。因此，推测有可能存在一种新型非线性弹性波并称其为摆型波。

Kurleny等（2000）从实测波形中分离出来的摆型波波形曲线，如图1。其中，tP和tS分别为纵波和横波到达时间，tμ为摆型波到达时间，t*为摆型波记录时间，VP和VS分别为纵波和横波波速，纵坐标为位移幅值用电压信号表示。在块系介质冲击作用下的动力响应试验以及深部爆炸和岩爆地震波谱分析中均证明了摆型波的存在及其非线性低频、低速特征。摆型波形成于一定冲击能量作用下的不同等级块系块体的错动和旋转过程中。

图1 地下爆炸时典型的位移波形Fig.1 Waveform of displacement generated by typical underground explosion.

Aleksandrova等（2008）给出摆型波在块系介质中的动力传播模型，如图2所示。其中mi为岩块质量，且岩块相比于块体间的软弱连接介质可抽象为刚体，整个块系岩体由n个岩块组成。岩块间的软弱连接介质简化为凯尔文粘弹性模型，其弹性系数为ki，阻尼系数为ci，外界冲击扰动为f（t），xi为第i岩块的位移响应。

下面对冲击载荷f（t）作用下摆型波传播过程中块系岩体的动力响应进行分析，进而研究由摆型波传播诱发的岩体超低摩擦。块系岩体动力响应方程的矩阵形式为

图2 摆型波动力传播模型Fig.2 Dynamic model of pendulum-type wave propagation.

式（1）中：

方程组（1）可变换为如下方程

令y（t）=［x（t） x·（t）］T，于是式（2-1）可降阶为

式（2-2）中：

令y=Фq，则在2n维状态空间中摆型波方程可表示为一阶微分方程组

由式（3）可知：在初始脉冲扰动f（t）作用下，式（2-2）的解为

式（4）中：Ф=［φ1…φ2n］，φi为矩阵B-1Aφi=φi／λ的广义特征向量；d=diag（eλ1t，eλ2t，…，eλ2nt），λi为广义特征向量φi所对应的特征值；q0=a-1ФTAy（0），a=ФTAФ=diag（a1，a2，…，a2n），y（0）为脉冲载荷f（t）作用下的初始条件，其中xi（0）=0，i=1，…，n，即初始时刻各块体的位移为零；1（0）=v，（0）=0，（i=2，…，n），即在脉冲载荷f（t）作用下初始岩块m1的扰动速度为v，其余块体的速度为零。由式（4）可知：

式（5）中：p=a-1ФTA。

2 块系岩体超低摩擦发生判据

下面分析在脉冲扰动f（t）作用下块系岩体的超低摩擦发生判据。令cir=φi，rpr，n+1=air+ birj，λr=αr+ωrj（αr＜0，j为虚数），则由上面的分析可知第i块岩块在脉冲载荷作用下的位移响应为

式（6）中：θir=arctan（bir／air），因此第i块与相邻块体i-1之间的相对位移为

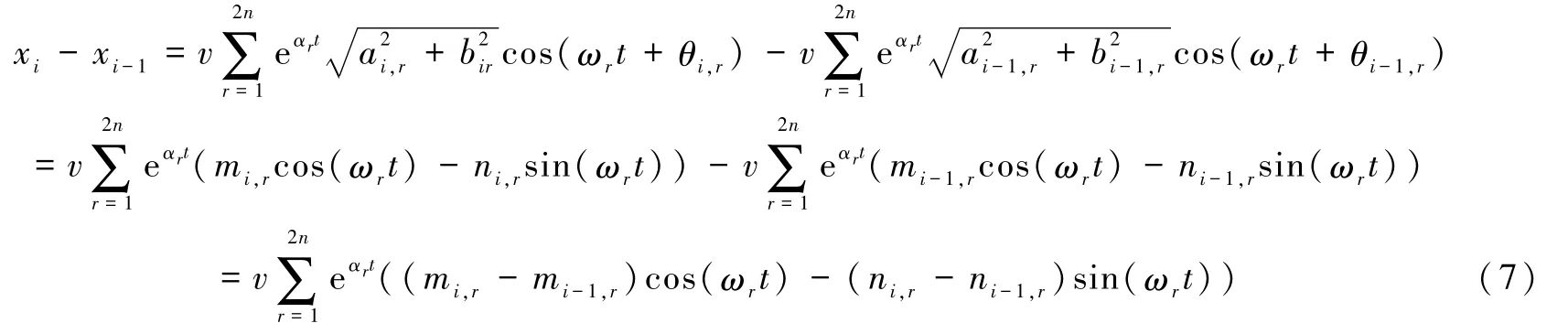
令mi，r-mi-1，r=li-1，r，ni，-ni-1，r=li，r，则式（7）可表示为

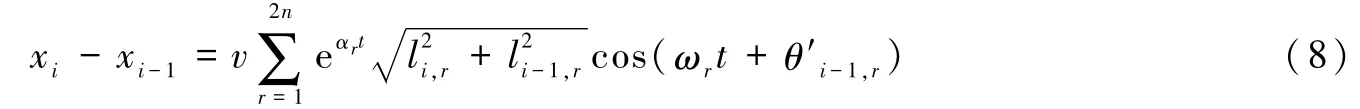
式（8）中，θ′i-1，r=arctan（lir／li-1，r），由此可知，相邻块体间的相对位移是由不同幅值、不同频率以及不同相位的余弦波叠加而成。由式（8）可知，块体间的软弱连接介质在脉冲载荷作用下呈现周期的拉伸和挤压变化。当相对位移xi-xi-1为正值时说明块体i-1与相邻块体i之间的软弱连接介质沿扰动传播方向被拉伸。我们关心的是拉伸最大值点，为此对式（8）求导得

式（9）中：φi-1，r=arctan（ωr／αr）。因此若对任意的r有

则块体i-1和块体i之间的相对位移xi-xi-1取得极值。由式（10）可知

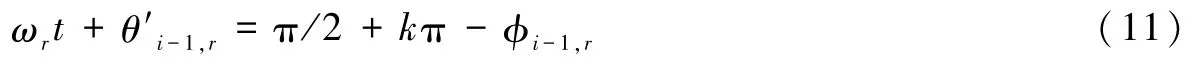
将式（11）代入式（8）可得

由于φi-1，r=arctan（ωr／αr）可知，因此，对任意的r若ωr＞0，在式（10）中k=2n，若ωr＜0，k=2n+1时，相对位移xi-xi-1取得极大值，此时对应着拉伸极值。同时，对任意的r若ωr＞0，在式（10）中k=2n+1，若ωr＜0，k=2n时，相对位移xixi-1取得极小值，此时对应着挤压极值。可以证明周期内其余极值点的幅值一定存在于这2个极值之间，因此这2个极值点分别是周期内的最大值和最小值。

当第i块和第i-1块之间具有超低摩擦倾向时，应满足

相对于超低摩擦现象，我们认为岩块间同样存在着“超强挤压”现象，且周期挤压规律满足

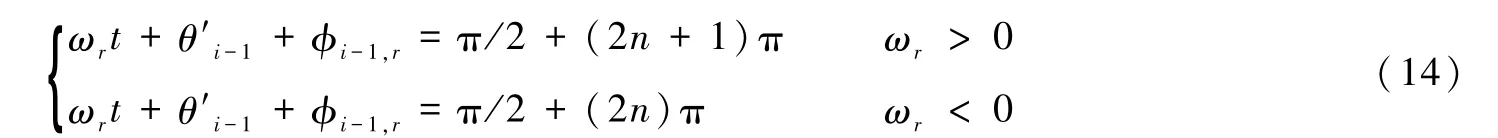
由上面的分析可知岩体的超低摩擦和超强挤压发生规律相同，只是有发生时间先后的差异。由此可见，超低摩擦和超强挤压周期交替发生，将岩块间的相对位移在拉伸方向上取得最大值时所对应的时刻称为准超低摩擦时刻

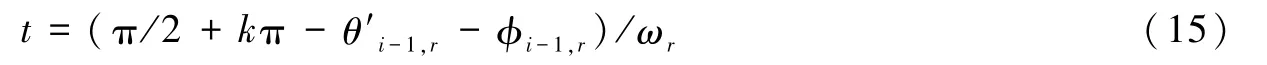
其中k为满足相对拉伸位移取得最大值的一个常数。若第i块和第j块两侧分别具有超低摩擦倾向时，则有

且

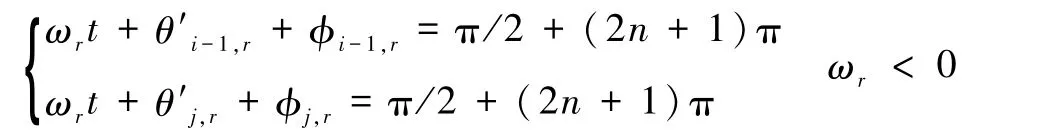
由此可得在脉冲载荷作用下局部岩体发生超低摩擦滑移的判据

此时，第i块至第j块之间的岩体在侧向力作用下容易滑出而诱发冲击地压等动力灾害。

从式（8）可知，在外界冲击扰动v一定的情况下，岩块间的相对位移由块系岩体的自身特性所决定，同时，外界扰动速度v不会改变岩体的超低摩擦发生规律，只会提高岩块间软弱连接介质的拉伸幅值。同时式（16）中的参数θ′i，r，φi，r均与块系岩体的M，C，K有关，下面通过计算分析块系岩体特性及扰动特性对超低摩擦的影响。

3 块系岩体超低摩擦计算分析

3.1 岩块尺度对超低摩擦影响分析

根据相关试验参数本文选取的原始计算参数为：岩块间粘性阻尼系数ci=20kg／s，弹性刚度系数ki=1×105kg／s2，各岩块的质量为mi=5kg，i=1，…，n，在脉冲载荷f（t）作用下初始岩块的扰动速度v=1m／s。下面分析块系岩体分别由不同尺度的岩块组成时，中间区域两块间的相对位移变化。假设整个块系岩体的总质量为100kg，根据质量守恒可计算块数为10块时每块的质量为10kg；块数为20块时每块的质量为5kg；块数为30块时每块的质量为3.33kg，且不同岩块尺度下块体间的粘弹性性质相同。则在脉冲扰动下不同尺度块系岩体中间两块的相对位移如图3。

当相对位移为正时，则表明块体间的软弱介质被拉伸，当相对位移为负值时，则表明块体间的软弱连接介质被压缩。我们关心的是拉伸最大值及其出现的时间点。由图3可知，在不同岩块尺度下块系岩体中间两块的相对位移最大值依次为3.0，1.5，1.1mm；所对应的时刻依次为0.38，0.37，0.45s。因此，随着岩块尺度的变小块系岩体中间区域2个块体间的最大拉伸值明显下降，同时所对应的时刻相对延后。由此当岩体节理较发育时，在中间区域发生超低摩擦的可能性有所下降。

图3 不同块体尺度下块系岩体中间两块的相对位移Fig.3 Relative displacement between intermediate rock blocks in different block scales.

下面利用10个块体组成的块系岩体进行计算分析，当改变局部岩块间的力学性质（粘弹性性质）及块体自身质量时，分析岩块间的相对位移变化特征。在不同条件下分别对第5块和第6块之间的相对位移x6-x5进行分析。

3.2 块系岩体特性对超低摩擦影响分析

3.2.1 岩块间弹性变化

当块体5和块体6之间的弹性系数分别下降为原来的50%（k5=0.5×105kg／s2）和25%（k5=0.25×105kg／s2）时，其余计算参数不变，则相对位移x6-x5如图4。

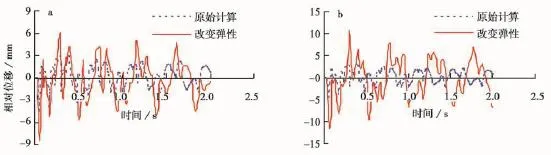
图4 块体5和块体6之间弹性下降时其相对位移变化Fig.4 Relative displacement between block 5 and 6 with a decreased elasticity.a块5和块6间弹性为原来的50%；b块5和块6间弹性为原来的25%

由图4可知，在原始计算参数下相对位移的最大值为3.0mm，所对应的时刻为0.38s。当块体5和块体6之间的弹性系数为原来的50%时，相对位移最大值为6.1mm，所对应的时刻为0.29s；当弹性系数为原来的25%时，相对位移最大值为10.7mm，所对应的时刻为0.30s。因此，岩块间的弹性系数下降时块体间的最大拉伸值反而增大，且最大值的出现时刻明显提前。岩块间的弹性下降幅度越大，块体间的最大拉伸值增大越明显，更易发生岩体超低摩擦。3.2.2 岩块间粘性变化

当块体5和块体6之间的粘性系数分别为原来的5倍（c5=100kg／s）和50倍（c5= 1000kg／s）时，其余计算参数不变，则相对位移x6-x5如图5。

由图5可知，当块体5和块体6之间的粘性系数为原来的5倍时，相对位移最大值为2.8mm，所对应的时刻为0.39s；当粘性系数为原来的50倍时，相对位移最大值为2.0mm，所对应的时刻为0.38s。因此，当岩块间的粘性系数增大时块体间的最大拉伸值下降明显，岩体间的超低摩擦效应有减弱的趋势。

图5 块体5和块体6之间粘性增大时其相对位移变化Fig.5 Relative displacement between block 5 and 6 with an increased viscidity.a块5和块6间粘性为原来的5倍；b块5和块6间粘性为原来的50倍

3.2.3 岩块质量变化

当块体5的质量分别为原来的50%（m5=2.5kg）和25%（m5=1.25kg）时，其余计算参数不变，则相对位移x6-x5如图6。

图6 块体5质量下降时第5和6块间相对位移变化Fig.6 Relative displacement between block 5 and 6 with a decreased mass of block 5.a第5块质量为原来的50%；b第5块质量为原来的25%

由图6可知，当块体5的质量为原来的50%时，相对位移最大值为2.0mm，所对应的时刻为0.18s；当质量为原来的25%时，相对位移最大值为2.0mm，所对应的时刻为0.18s。由此可知，岩块质量下降时块体间的最大拉伸值下降明显，且出现时刻明显提前，但块体质量的下降程度对最大拉伸值及其出现时刻影响较小。因此，局部岩块质量下降时会导致岩体间的超低摩擦明显减弱。

3.3 外界周期扰动对超低摩擦影响分析

下面分析外界周期扰动频率对岩块间相对位移变化的影响，仍然采用10个岩块进行计算分析，且块系岩体的计算参数不变。令外界周期扰动函数为f（t）=p sin（ωt），则第i块和第i-1块之间的稳态相对位移可表示为

式（17）中

由式（18）进一步可得

其中

由于低频扰动对岩体的稳定影响更大，选取扰动频率在20Hz以下进行分析，同时令稳态激振力p=50N。研究在不同扰动频率ω下块体5和块体6之间的相对位移x6-x5的变化。

（1）扰动频率为2Hz时，相对位移x6-x5的变化如图7。

其中瞬态相对位移是由脉冲载荷引起的块体间相对位移，且在脉冲载荷作用下初始岩块m1扰动速度为1m／s。稳态相对位移是由外界周期扰动f（t）=p sin（ωt）所引起的，而相对位移为瞬态相对位移和稳态相对位移的叠加。

由前面的计算可知块体5和块体6之间的瞬态相对位移最大值为3.0mm，所对应的时刻为0.38s。同时由图7可知，当外界扰动频率为2Hz时，稳态相对位移最大值为0.3mm，所对应的时刻为1.69s。块体间最后表现出来的最大相对位移为2.9mm，所对应的时刻为0.38s。此时在外界周期扰动作用下，岩块间的最大拉伸值下降0.1mm，但最大值出现时刻不变。

（2）扰动频率为5Hz时，相对位移x6-x5的变化如图8。

图7 扰动频率ω=2时第5和6块间相对位移变化Fig.7 Relative displacement between block 5 and 6 at the perturbation frequencω=2.

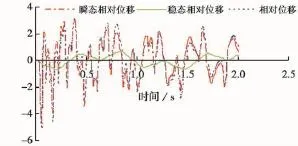
图8 扰动频率ω=5时第5和6块间相对位移变化Fig.8 Relative displacement between block 5 and 6 at the perturbation frequencyω=5.

当外界扰动频率为5Hz时，稳态相对位移的最大值为0.7mm，所对应的时刻为0.85s。块体间最后表现出来的最大相对位移为3.3mm，所对应的时刻为0.39s。此时在外界周期扰动作用下，岩块间的最大拉伸值增大0.3mm，同时出现时刻延后0.01s。

（3）扰动频率为14Hz时，相对位移x6-x5的变化如图9。

当外界扰动频率为14Hz时，稳态相对位移的最大值为9.7mm，所对应的时刻为1.64s。块体间最后表现出来的最大相对位移为11.8mm，所对应的时刻为1.65s。此时在外界周期扰动作用下，岩块间的最大拉伸值增大8.8mm，同时出现时刻延后1.27s。此时的扰动频率接近块系岩体的准共振频率。

（4）扰动频率为17Hz时，相对位移x6-x5的变化如图10。

当外界扰动频率为17Hz时，稳态相对位移最大值为6.7mm，所对应的时刻为1.48s。块体间最后表现出来的最大相对位移为7.9mm，所对应的时刻为1.09s。此时在外界周期扰动作用下，岩块间的最大拉伸值增大4.9mm，同时出现时刻延后0.71s。

图9 扰动频率ω=14时第5和6块间相对位移变化Fig.9 Relative displacement between block 5 and 6 at the perturbation frequencyω=14．

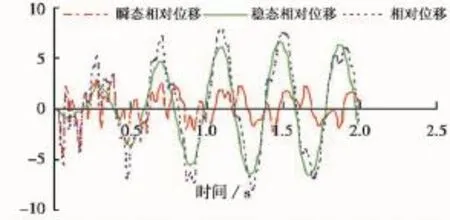
图10 扰动频率ω=17时第5和6块间相对位移变化Fig.10 Relative displacement between block 5 and 6 at the perturbation frequencyω=17．

（5）扰动频率为20Hz时，相对位移x6-x5的变化如图11。

当外界扰动频率为20Hz时，稳态相对位移的最大值为2.6mm，所对应的时刻为1.88s。块体间最后表现出来的最大相对位移为5.1mm，所对应的时刻为0.28s。此时在外界周期扰动作用下，岩块间的最大拉伸值增大2.1mm，同时出现时刻提前0.1s。

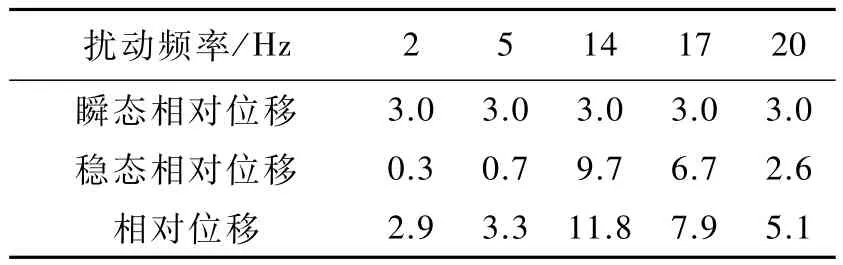
表1 不同扰动频率下相对位移x6-x5的最大值Table 1 Maximum of relative displacement between block 5 and 6 at different perturbation frequencies

图11 扰动频率ω=20时第5和6块间相对位移变化Fig.11 Relative displacement between block 5 and 6 at the perturbation frequencyω=20．

从表1可知，在脉冲载荷作用下，块体间呈现瞬态相对位移且最大值为3.0mm，同时，在外界周期扰动作用下，块体间呈现稳态相对位移且不同扰动频率下的稳态相对位移有较大的差别。在脉冲载荷和外界周期扰动的叠加作用下块体间会出现2种动载荷叠加作用下的相对位移。当扰动频率为14Hz时（接近准共振频率），岩块间的稳态相对位移最大值迅速增大，同时扰动频率在14Hz两侧取值时，稳态相对位移的最大值有逐渐下降的趋势。外界周期扰动会使岩体超低摩擦表现得更明显，即在2种动载荷叠加后的相对位移相比脉冲载荷作用时的瞬态相对位移明显增大，如（5，14，17，20Hz），同时，周期扰动也存在使超低摩擦减弱的表现，如2Hz。

3.4 外界扰动幅值对超低摩擦影响分析

下面研究在外界周期扰动频率一定时，扰动幅值对岩块间相对位移的影响。令外界扰动频率ω=5Hz，稳态激振力幅值p分别为p=100N和150N。

（1）稳态激振力p=100N时，相对位移x6-x5的变化如图12。

当外界激振力幅值p=100N时，稳态相对位移的最大值为1.4mm，所对应的时刻为0.85s与p=50N（图8）时相比最大值增大0.7mm，且出现时刻不变。此时，块体间最后表现出来的最大相对位移为3.6mm，所对应的时刻为0.39s，与p=50N时相比最大相对位移增大0.3mm，且出现时刻不变。

（2）稳态激振力p=150N时，相对位移x6-x5的变化如图13。

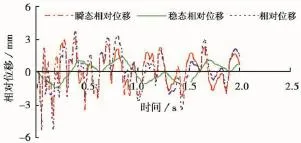
图12 扰动幅值p=100N时第5和6块间相对位移变化Fig.12 Relative displacement between block 5 and 6 at the perturbation amplitude p=100N.

图13 扰动幅值p=150N时第5和6块间相对位移变化Fig.13 Relative displacement between block 5 and 6 at the perturbation amplitude p=150N.

当外界激振力幅值p=150N时，稳态相对位移的最大值为2.1mm，所对应的时刻为0.85s，与p=100N时相比最大值增大0.7mm，且出现时刻不变。此时，块体间最后表现出来的最大相对位移为4.0mm，所对应的时刻为0.39s，与p=100N时相比最大值增大0.4mm，且出现时刻不变。因此，外界激振力幅值p的变化只会改变块体间拉伸最大值的大小，不会改变其出现的时刻，因此激振力幅值p越大，岩体间越容易发生超低摩擦。

4 结论

（1）基于摆型波理论研究了块系岩体超低摩擦发生规律，由此提出煤岩错动型冲击地压的超低摩擦机理，即摆型波在煤岩体中传播时块体间的相对位移达到最大值时，在侧向力作用下容易诱发煤岩体滑移冲击。

（2）通过动力传播下岩块间的相对位移动态变化规律研究，给出了块系岩体超低摩擦发生判据。在块系岩体动力传播过程中相邻块体间存在着拉伸和挤压交替变化，当达到拉伸最大值时，相邻块体间出现最大的“剥离”状态，正压力较小，此时在侧向力作用下岩块容易向侧向滑出。由此，将相邻块体间出现拉伸最大值作为岩体超低摩擦的发生判据。

（3）一定区域内的块系岩体当组成岩体的块度越小则中间块体间的最大拉伸值越小，同时岩块间的阻尼增大或块体质量下降时，块体间的最大拉伸值也出现下降变化，此时岩体发生超低摩擦的可能性较小。但当岩块间的弹性系数下降时，块体间的最大拉伸值明显增大，此时岩体发生超低摩擦的可能性较大。

（4）外界扰动频率会改变岩块间的最大拉伸值。当扰动频率接近块系岩体的准共振频率时，最大拉伸值急剧增大，当远离共振频率取值时，最大拉伸值逐渐下降。此外，外界扰动幅值只会改变最大拉伸值的幅值大小，而不会改变其出现的时间。

钱七虎.2004.深部地下空间开发中的关键科学问题［R］见：第230次香山科学会议：深部地下空间开发中的基础研究关键技术问题.北京.2004.

QIAN Qi-hu.The key problems in deep underground space development［R］.In：The 230th Xiangshan Academic Conference：Basic Crucial Problems in Deep Underground Space Development，Beijing，2004（in Chinese）.

潘一山，王凯兴.2012.岩块尺度对摆型波传播影响研究［J］.岩石力学与工程学报，31（supp l 2）：3459—3465.

PAN Yi-shan，WANG Kai-xing.2012.Study on effect of block-rock scale on pendulum-type wave propagation［J］. Chinese Journal of Rock Mechanics and Engineering，31（suppl 2）：3459—3465（in Chinese）.

吴昊，方秦，王洪亮.2008.深部块系岩体超低摩擦现象的机理分析［J］.岩土工程学报，30（5）：769—775.

WU Hao，FANG Qin，WANG Hong-liang.2008.Mechanism of anomalously low friction phenomenon in deep block rock mass［J］.Chinese Journal of Geotechnical Engineering，30（5）：769—775（in Chinese）.

王明洋，戚承志，钱七虎.2005.深部岩体块系介质变形与运动特性研究［J］.岩石力学与工程学报，24（16）：2825—2830.

WANG Ming-yang，QI Cheng-zhi，QIAN Qi-hu.2005.Study on deformation and motion characteristics of blocks in deep rock mass［J］.Journal of Rock Mechanics and Engineering，24（16）：2825—2830（in Chinese）.

姚路，马胜利.2013.断层同震滑动的实验模拟：岩石高速摩擦实验的意义、方法与研究进展［J］.地球物理学进展，28（2）：607—623.

YAO Lu，MA Sheng-li.2013.Experimental simulation of coseismic fault sliding：Significance，technologicalmethods and research progress of high-velocity frictional experiments［J］.Progress in Geophysics，28（2）：607—623（in Chinese）.

Aleksandrova N I，Chernikov A G，Sher E N.2006.On attenuation of pendulum-type waves in a block rock mass［J］. Journal of Mining Science，42（5）：468—475.

Aleksandrova N I，Sher E N.2004.Modeling of wave propagation in block media［J］.Journal of Mining Science，40（6）：579—587.

A leksandrova N I，Sher E N，Cherniko A G.2008.Effect of viscosity of partings in block-hierarchical media on propagation of low frequency pendulum waves［J］.Journal of Mining Science，44（3）：225—234.

Kurlenya M V，Oparin V N，Vostrikov V I.1999.Effect of anomalously low friction in block media［J］.Journal of Applied Mechanics and Technical Physics，40（6）：1116—1120.

Kurlenya M V，Oparin V N.1999.Geomechanics，problems of nonlinear geo-mechanics（PartⅠ）［J］.Journal of Mining Science，36（4）：12—16.

Kurlenya M V，Oparin V N.2000.Geomechanics，problems of nonlinear geomechnics（partⅡ）［J］.Journal of M ining Science，36（4）：305—326.

Kurlenya M V，Oparin V N，Vostrikov V I.1993.Formation of elastic wave packages in the block-structured medium under impulse loading pendulum type waves［J］.Dokl Akad Nauk SSSR，333（4）：1—7.

Kurlenya M V，Oparin V N，Vostrikov V I.1996.Pendulum-type waves，partⅡ：Experimental methods and main results of physicalmodeling［J］.Journal of M ining Science，32（4）：245—273.

Sadovsky M A.1979.Natural lumpiness of rocks［J］.Dok l AN SSSR，247（4）：21—29.

Wang Kai-xing，Pan Yi-shan，Nadegda Dergachova.2013.Steady-state response and resonance condition of block rock mass on external periodic excitation［J］.Mathematical Methods and Physicomechanical Fields，56（1）：94—101.

PENDULUM-TYPE W AVES THEORY ON THE M ECHANISM OF ANOM ALOUSLY LOW FRICTION BETW EEN ROCK M ASSES

PAN Yi-shan WANG Kai-xing

（School of Mechanics and Engineering，Liaoning Technical University，Liaoning，Fuxin 123000，China）

When rock burst occurs in deep coalmine，there is a significant phenomenon of rupture in coal and rock mass.Based on the theory of pendulum-type wave's propagation in the block rock mass，the mechanism of anomalously low friction between rock blocks is studied.Block rock mass is composed of rock block and the weak medium between rock blocks.The law of anomalously low friction in rock mass is studied bymaximum value of relative displacement between rock blocks under dynam ic action. The softmedium between rock blocks has periodic tensile and compressive variations under the effect of blocks during pendulum-type wave's propagation in block rock mass.When relative displacement of softmedium between rock blocks reaches the maximum value in the tensile direction，the adjacent blocks would show an obvious separation state.At this time，positive pressure between rock blocks is small relatively and rock block is easy to slide under lateral force in themechanism of anomalously low friction between rock blocks.As a result，the criterion for block rock mass'anomalously low friction is put forward.Based on the dynamic model of pendulum-type wave's propagation，this paper analyzes the relative displacement between rock blocks under the effect of various external perturbations including the transient perturbation and periodical perturbation，as well as the transient state response and steady state response of block rock mass.The effect of mass of local block and viscoelasticity property of softmedium between rock blocks on the relative displacement between local rock blocks is calculated.When the viscous coefficient in block partings increases or the mass of rock block decreases，the maximum tensile value between rock blocks decreases，at this moment，the anomalously low friction does not act easily.However，when the elasticity coefficient in block partings decreases，the maximum tensile value between rock blocks increases obviously，at this moment，the anomalously low friction acts easily.Meanwhile，the effect of external disturbance property on anomalously low friction in rock mass is analyzed.Changing external disturbance frequency will lead to change of maximum tensile value between rock blocks，which will rise sharply at the disturbance frequency close to the quasi-resonant frequency and decline gradually at the disturbance frequency far away from the quasi-resonant frequency.It is important for understanding the laws of faultmovement type rock burst through the analysis of the anomalously low friction mechanism of rock mass based on propagation of pendulum-type waves.

rock mechanics，block rock mass，pendulum-type waves，anomalously low friction

P313

A

0253-4967（2014）03-0833-12

潘一山，男，1964生，1999年在清华大学获固体力学专业博士学位，教授，博士生导师，主要从事固体力学和岩石力学方面的研究工作，E-mail：panyish_cn＠sina.com。

10.3969／j.issn.0253-4967.2014.03.022

2014-07-14收稿，2014-09-09改回。

国家重点基础研究发展规划项目（2010CB226803）和国家自然科学基金（51404129）共同资助。