不可逆汽机热泵性能优化研究
赵 麒,刘丽莘,韩风毅,王 琛
(1.长春工程学院能源动力工程学院;2.长春工程学院建筑设计研究院,长春130012)
0 引言
国内外学者A Bejan,L G Chen等以探索热力过程的性能界限、热力学优化目标的问题开展了广泛深入的研究,在物理学领域取得了很多研究成果[1-2]。A Durmayaz[3]以热力学、传热学、流体力学和其他传输过程的基本理论相结合,在有限时间和有限尺寸约束条件下,优化存在不可逆性的实际热力系统性能。Badescu[4]提出了一个由太阳能驱动的内可逆卡诺热机航天动力站模型,他获得了最大功率输出并优化了太阳能集热器和辐射面积的最佳配比。Wu and Kiang[5]介绍了内部不可逆卡诺热机的性质可由名为周期不可逆参数的单参数确定。Salah El Din[6]研究了变温位不可逆卡诺热机,他得出冷热量侧流体的最佳工作温度和最大输出功率是换热器进口的温度而不是进口和出口的平均温度。
陈金灿等[7]确定了不可逆辐射卡诺热机最大输出功率时的效率和相应的最佳工作流体温度和传热面积[8-11]。完成了吸收式热泵的相似分析,建立了一个通用的不可逆吸收式制冷循环模型,模型包括了流体和外部热源间有限传热、热池向冷空间的散热、流体内部分散的不可逆性,用此模型在总换热面积一定的情况下计算了最大cop和系统冷负荷率,此后研究了不可逆四温位不可逆吸收式制冷循环的性能。陈林根等[12]研究了带有变温热源的可再生不可逆闭式Joule-Brayton循环性能。
本文建立了不可逆汽机热泵的数学模型,在总换热面积一定的前提下,对系统热负荷与系统性能系数进行优化研究,为实际汽机热泵的设计与运行提供理论基础。

图1 汽机热泵系统原理图
1 系统模型
汽机热泵系统工作原理如图1,由动力循环和压缩式热泵循环两部分组成,包括汽机、压缩机、蒸发器、冷凝器和节流阀。动力部分的高温热源温度为TH,向低温热源TL放热,汽机中蒸汽做功,温度由T1降至T2,蒸汽做功产生的机械能驱动热泵的压缩机工作。热泵由汽机带动,从低温热源T4吸热,向高温热源T3放热,热泵蒸发器与冷凝器中工质的工作温度分别为Te、Tc。
根据传热定律,汽机高温侧、低温侧、冷凝器和蒸发器的换热分别为

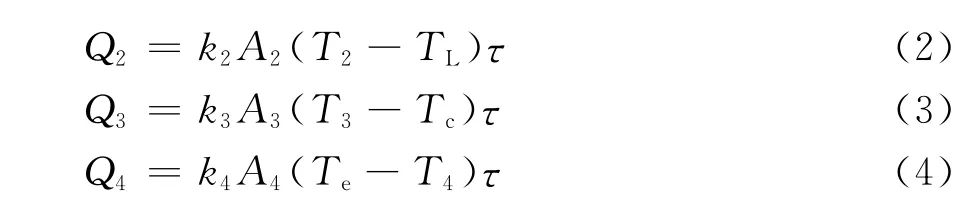
k1、k2、k3、k4分别为汽机高温侧、低温侧、冷凝器和蒸发器的换热系数,A1、A2、A3、A4分别为汽机高温侧、低温侧、冷凝器和蒸发器的换热面积,τ为系统循环时间。根据热力学第一定律

引入总换热面积A,由下式确定,且保持不变。
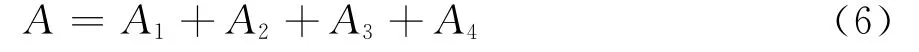
定义a为冷凝器与低温侧换热量之比。

假设热空间与环境间的热漏满足线性传热规律,

由热力学第二定律,引入不可逆因子I,
I=1时,循环为可逆循环,I>1时,循环为不可逆循环。
2 性能优化
有上述模型和热力学第二定律
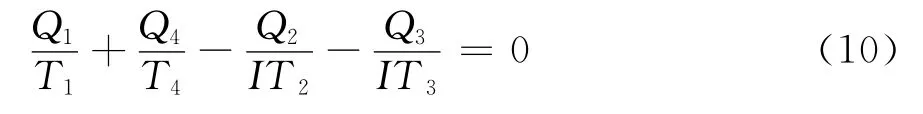
由热负荷定义

引入系统性能系数
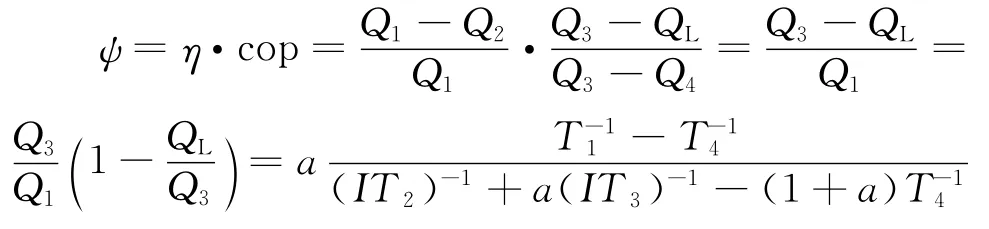


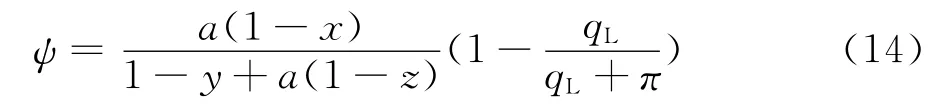
引入拉格朗日函数

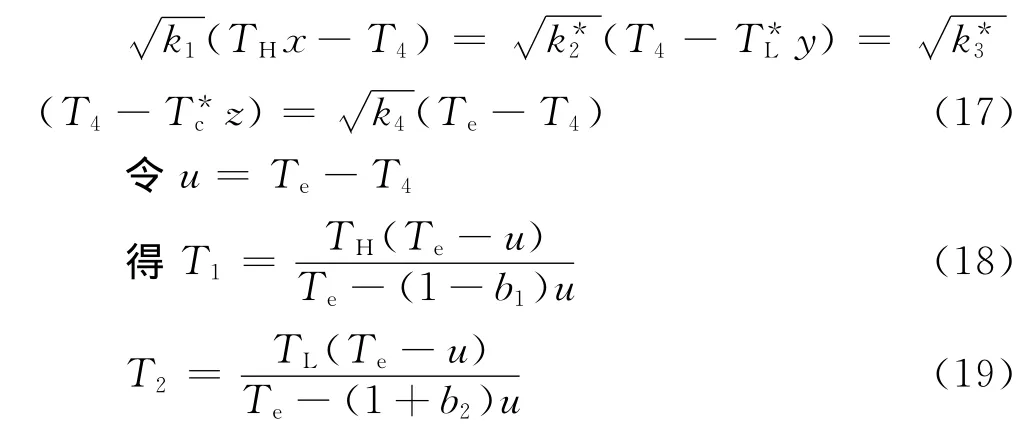
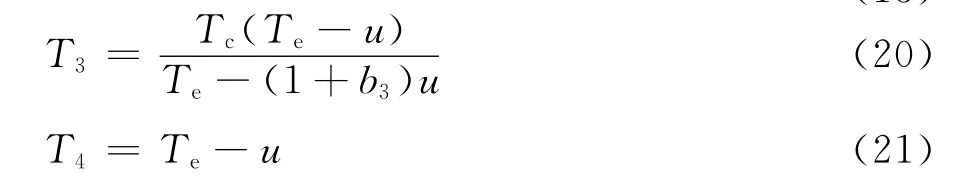
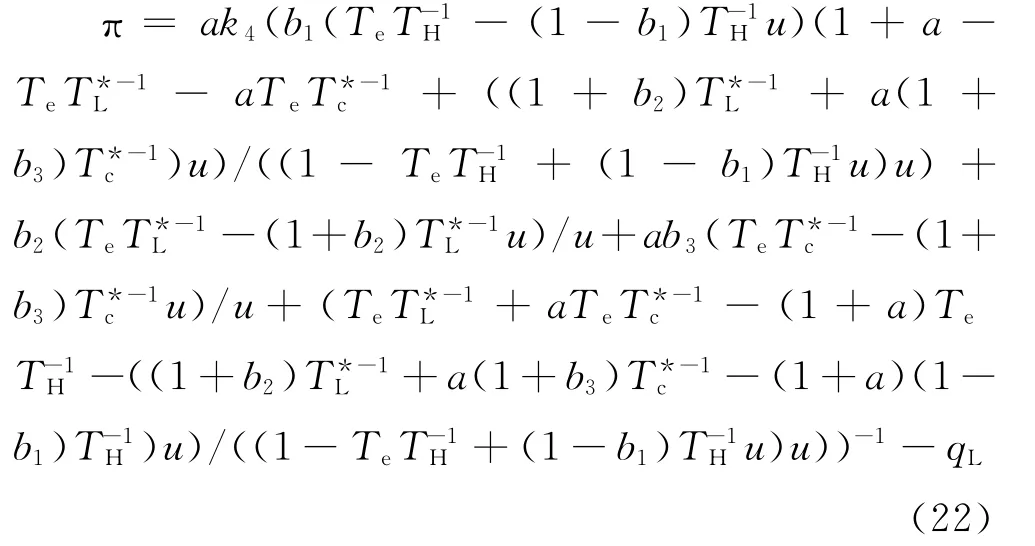
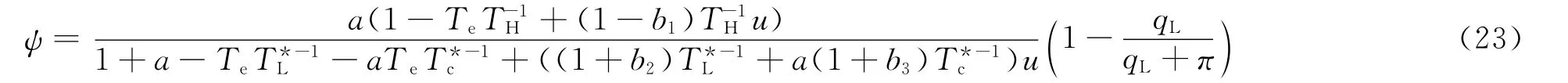
3 分析与讨论
为分析系统的性能,引入算例进行分析。
计算条件:k1=k2=k3=k4=0.5k·W/K·m2,A =10m2,TH=623K,TL=534K,Te=293K,Tc=333K。
图2、图3为蒸发器换热温差和不可逆性对系统性能的影响(KL=0,a=1),热负荷随蒸发器换热温差的增加而增大,系统性能系数随之减小,相同换热温差时,不可逆性越大,热负荷与系统性能系数均越小。I=1时,换热温差由5℃升至30℃,热负荷上升了6.21倍,系统性能系数下降了28.22%;I=1.05时,换热温差由5℃升至30℃,热负荷上升了5.52倍,系统性能系数下降了25.29%。传热温差为18℃时,I=1.05相比I=1.00系统的热负荷与性能系数分别下降了69.34%和7.39%。

图2 不可逆性对热负荷的影响
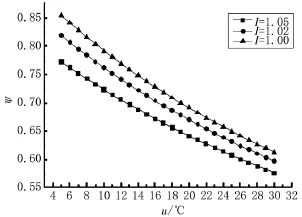
图3 不可逆性对系统性能系数的影响
图4、图5为蒸发器换热温差和热漏对系统性能的影响(I=1,a=1)热负荷随蒸发器换热温差的增加而增大,相同传热温差时热漏系数越大,热负荷越小。KL=0.02时,换热温差由5℃升至30℃,热负荷上升了16.56倍;传热温差为18℃ 时,KL=0.01与KL=0.03对应的热负荷下降了16.98%。系统的性能系数在存在热漏的情况下随蒸发器换热温差的增加先迅速增加达最大值后逐渐略有减小,KL=0.01、KL=0.02、KL=0.03在u=15℃、u=17℃、u=22℃达最大系统性能系数,分别为0.667、0.599、0.549。
图6、图7为蒸发器换热温差和冷凝器与低温侧换热量比对系统性能的影响(KL=0,I=1),热负荷随蒸发器换热温差的增加而增大,系统性能系数随之减小,相同换热温差时,冷凝器与低温侧换热量比越大,热负荷与系统性能系数均越大。a=5时,换热温差由5℃升至30℃,热负荷上升了86.28%,系统性能系数下降了33.84%,传热温差为18℃时,a=5相比a=0.5系统的热负荷与性能系数分别上升了41.63% 和159.57%。

图4 热漏对热负荷的影响
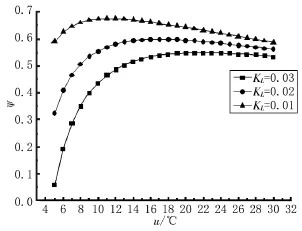
图5 热漏对系统性能系数的影响

图6 冷凝器与低温侧换热量比对热负荷的影响
4 结论
应用有限时间热力学对考虑热阻、热漏和内部不可逆性对汽机热泵系统的性能影响进行了分析。通过数值算例研究了循环参数对系统性能系数ψ和热负荷的影响,结果适用于符合牛顿传热规律的所有汽轮机热泵系统,并为汽机热泵系统性能改进与优化提供一些理论指导。

图7 冷凝器与低温侧换热量比对系统性能系数的影响
[1]Bejan A.Entropy generation minimization:the new thermodynamics of finite-size and finite-time process[J].Applied Physics,1996,79(3):1191-1218.
[2]Chen LG,Wu C,Sun FR.Finite time thermodynamics optimization or entropy generation minimization of energy system[J].Journal of Non-equilibriumThermodynamics,1999,24(4):327-359.
[3]Durmayaz A,Sogut OS,Sahin B,etc.Optimization of thermal systems base on finite-time thermodynamics and thermoeconomics[J].Progress in Energy and Combustion Science,2004,30(3):175-217.
[4]Badescu V.Optimum design and operation of a dynamic solar power system[J].Energy Convers Mgmt,1996,37(2):151-160.
[5]Wu C,Kiang RL.Finite-time thermodynamic analysis of a Carnot engine with internal irreversibility[J].Energy,1992,17(12):1173-1178.
[6]Salah El-Din MM.Second law analysis of irreversible heat engines with variable temperature heat reservoirs[J].Energy Convers Mgmt,2001,42(2):189-200.
[7]Chen J,Wu C,Kiang RL.Maximum specific power output of an irreversible radiant heat engine[J].Energy Convers Mgmt,1996,37(1):17-22.
[8]Chen J,Andresen B.Optimal analysis of primary performance parameters for an endoreversible absorption heat pump[J].Heat Recovery Syst CHP,1995,15(8):723-731.
[9]Chen J,Schouten JA.Optimum performance characteristics of an irreversible absorption refrigeration system[J].EnergyConvers Mgmt,1998,39(10):999-1007.
[10]Chen J.The optimum performance characteristics of a four-temperature-level irreversible absorption refrigerator at maximum specific cooling load[J].J Phys D:Appl Phys,1999,32:3085-3091.
[11]Chen J.The general performance characteristics of an irreversible absorption heat pump operating between four temperature levels[J].J Phys D:Appl Phys,1999,32:1428-1433.
[12]Chen LG,Sun FR,Wu C,etc.Theoretical analysis of the performance of a regenerative closed Brayton cycle with internal irreversibilities[J].Energy Convers Mgmt,1997,3(9):871-877.

