农村固体废弃物回收逆向物流网络优化

柴月珍

(重庆大学数学与统计学院，重庆 401331)

农村固体废弃物回收逆向物流网络优化

柴月珍

(重庆大学数学与统计学院，重庆 401331)

针对农村固体废弃物回收，以减少废弃物堆积、获得回收效益为目标，在混合整数线性规划方法的基础上建立了一种多产品、侧重回收、有能力限制的逆向物流网络优化设计模型。据此确定各初级回收代理点和集中回收处理中心的建立，使各种设施的投资和运营成本以及处理成本之和最小。利用Benders算法求解该模型，并通过算例验证了模型的有效性。

农村;多产品;有能力限制;逆向物流;混合整数线性模型

随着科学技术的进步和顾客消费水平的提高，企业的创造能力也不断提升，随之而来的是社会产品更新替代越来越频繁。资源短缺、环境恶化是目前社会所面临的较为严重的问题。随着农村生活水平的不断提高，农村的固体废弃物产生总量也有显著增加，但农村地区的物流基础设施建设仍相对落后，为农村逆向物流的发展带来很多不便。

长期以来，有关废弃物回收处理的研究都集中在大城市、单一产品的回收处理方面，而针对农村或乡镇地区的较杂乱的多种固体废弃物处理回收方面的文献则较少。文献［1］分析了农村废弃物回收逆向物流的特点及存在的问题;文献［2］提出了农村逆向物流的含义及发展农村逆向物流的意义，并在此基础上设计了适用于农村的逆向物流网络结构;文献［3］提出了多级逆向物流网络结构，建立的0－1混合整数规划模型实现了逆向物流网络的选址/分配问题，该模型兼顾了个客户群的产品回收便利性;文献［4］关于单产品、有能力限制的产品回收建立了基于混合整数线性规划方法的逆向物流网络优化模型，据此确定了网络中各设施的数量及位置，以及该网络路径上的物流量分配。这些文献中的物流网络模型都以总成本最小为目标。事实上，根据中国农村的性质和特点，在中国广大农村地区，包含检测、拆解在内的大型逆向物流网络很难实施，即着重于农村废弃物回收的逆向物流网络还需要城市物流网络设施的配合［5］。

1 模型建立

1.1 模型描述

针对小型城市及其周边区县(主体为周边区县农村地区)所建立的固体废弃物回收逆向物流网络，各区县会设多个初级回收点。为提高资源利用率，缓解市区的交通拥堵状况，从每个县现有(或新建)的初级回收点中选取一个代理该县的废弃物处理及运输，即其他初级回收点所回收的废品全部送往该地点，然后由该回收点集中运往集中处理中心。

模型1图1为逆向物流网络图。在该网络图中，P表示区县P建立初级回收代理处理点;C表示集中回收处理中心;D表示废弃物处理点;I表示各检测中心;R表示再利用再制造中心;S表示拆解中心，初级回收点分散在各区县的各个村。由于大多数市的各区县分布在市区的周围，考虑到集中回收处理中心的作用以及城市的交通状况，选择在市区的边缘地区根据实际情况建立多个集中回收处理中心。C处对固体废弃物分类处理，其中部分废弃物将被直接送往D处，剩余部分则进行分类送检或是直接送往R。经检测还可利用的废弃物和拆解处理后的部件可用的均送往R进行加工再造。

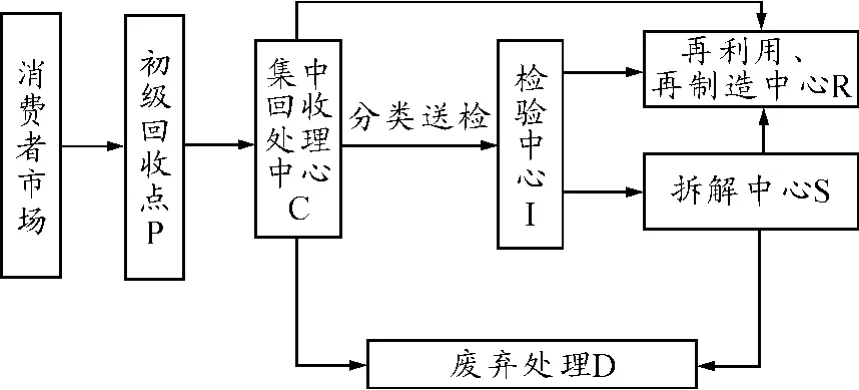
图1 逆向物流网络

1.2 模型假设

1)所有回收任务由初级回收点完成;新建初级回收中心除回收废品外都作为初级回收代理点使用。

2)在初级回收点回收的废品种类是不确定的，但各初级回收点废旧产品的回收量、单位运营成本、设施间的运输费用、单位废弃处理费用等已知。

3)假定同一区县的各初级回收点对同一种类废品的单位回收成本和单位运输成本相同。

4)回收品送至检测中心时不考虑材料损耗，在拆解中心则要考虑材料损耗，损耗部分全部流向废弃处理中心;拆解下来的有用零件仅受回收量限制。

5)假设物流系统中共有J种商品存在，j∈J。第j种商品在“单位重量·路程”的单位运输费用可根据该地区的消费情况获得。

6)由于新建以及场地等的影响，新建的初级回收代理点和集中回收处理中心的处理能力是有限的。

1.3 参数描述

1.3.1 序列集合

市周边有P个区县，p∈P，由于每区县只有一个初级回收代理点，则P也表示初级回收代理点的集合;Pn表示每个区县现有的初级回收点集合，有pn∈PN;C为集中回收处理中心的集合，c∈C;R为再利用再制造中心点，r∈R;I为检测中心地点集合，i∈I;S为拆解中心，s∈S;D为废弃处理点集合，d∈D;J表示初级回收点回收的废品的种类集合，j∈J;jK表示废品j的分类集合，k∈K，jk∈JK。

1.3.2参数

Apjk表示在一定时期内初级回收点p回收的废旧物品jk的数量(不同种类废弃物品单位不同，不具体标注)，pn∈PN，jk∈JK。Apjk表示在区县p废弃物品jk的单位回收成本，p∈P，jk∈JK;Ap表示在区县p新建(或扩建)一初级回收点并投入运营的成本费用;Ac表示新建集中回收处理中心c并投入运营的成本费用;Bpjk表示由初级回收点pn运往初级回收代理点p的回收品jk的单位运输费用，pn∈PN，jk∈JK;Bpcjk表示初级回收代理点p运往集中回收处理中心c的回收品jk的单位运输费用，p∈P，jk∈JK;Bcijk表示由集中回收中心c运往检测中心i的回收品jk的单位运输费用，i∈I，jk∈JK;Bcdjk为由集中回收处理中心c送往废弃处理中心d的废弃物品jk的单位运输费用，d∈D，jk∈JK;Bcrjk为由集中回收处理中心c运往再利用再制造中心r的回收品jk的单位运输费用，r∈R，jk∈JK;集中回收处理中心c对回收品jk的单位处理成本为jk∈JK;检测中心i对回收品jk的单位检测成本为Bi

jk，i∈I，jk∈JK;拆解中心s对回收品jk的单位拆解费用为Bsjk，s∈S，jk∈JK;在集中处理中心回收品jk不送往检测中心时，jk的材料损耗率为δj;在拆解中心s回收品jk的材料损耗率为φj;在一定时期内新建的集中回收处理中心c对废弃物jk的最大处理能力为ucjk;新建初级回收代理点p对废弃物jk的最大处理能力为vpjk。该市最多建立g个集中回收处理中心，h个初级回收代理处理点。

1.3.3 变量

Xpnjk为由初级回收点pn运往初级回收代理点p的回收品jk的运输量，pn∈PN，jk∈JK;Xpcjk为初级回收代理点p运往集中回收处理中心c的回收品jk的运输量，p∈P，c∈C，jk∈JK;Xcijk为由集中回收中心c运往检测中心i的回收品jk的运输量，c∈C，i∈I，jk∈JK;Xisjk为由检测中心i运往拆解中心s的回收品jk的运输量，i∈I，s∈S，jk∈JK;Xirjk为由检测中心i运往再利用再制造中心r的回收品jk的运输量，i∈I，r∈R，jk∈JK;Xcdjk为由集中回收处理中心c送往废弃处理中心d的废弃物品jk的数量，c∈C，d∈D，jk∈JK;Xcrjk为由集中回收处理中心c运往再利用再制造中心r的回收品jk的运输量，c∈C，r∈R，jk∈JK;Xsrjk为由拆解中心s运往再利用再制造中心r的回收品jk的运输量，s∈S，r∈R，jk∈JK;Xsdjk为由拆解中心s送往废弃处理中心d的废弃物品jk的运输量，d∈D，s∈S，jk∈JK; Yp为0－1变量，表示是否在区县p新建初级回收点，是取1，否取0;Yc为0－1变量，表示是否在区域c建立集中回收处理中心，是取1，否取0;Yijk为0－1变量，表示是否将集中回收处理中心的回收品运往检测中心i，是取1，否取0;Yrjk为0－1变量，表示是否将集中回收处理中心的回收品直接运往再利用再制造中心r，是取1，否取0。

1.4 模型建立c∈C

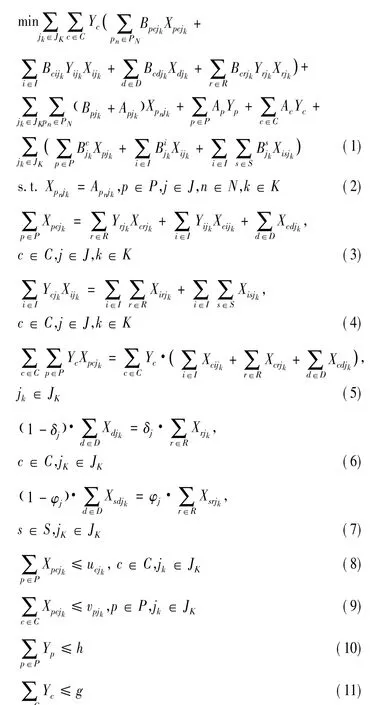
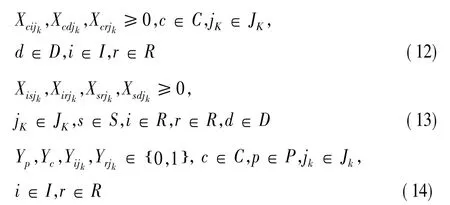
目标式(1)表示设计该回收逆向物流网络时，要使各物流量设施的投资、设施间的运输成本、回收成本以及回收品处理成本之和最小;式(2)表示初始条件;约束式(3)～(6)表示逆向物流守恒量条件;式(5)、(6)表示逆向物流过程中的材料损耗;式(7)、(8)表示新建设施的处理能力限制;式(9)、(10)表示新建设施的数量约束;式(11)～(13)规定了各变量的取值范围。

2 模型应用算例

2.1 算法分析

该模型为混合整数线性模型，其求解方法是多样的。为提高求解效率，本文采用Benders分解算法［6］。

2.2 算例应用

针对越来越多的产品回收逆向物流，需要考虑的信息越来越复杂，在专门针对多产品废旧物品回收建立的逆向物流网络优化系统中，暂不考虑企业的利润，只考虑假设条件下的成本问题。现对某一城市及其周边区县进行逆向回收网络规划，计划设初级回收中心和代理回收处理中心，以及集中回收处理中心，以方便各区县各村落的废旧物品回收。假设区县的个数是5，每个区县有n=3个初级回收点和1个代理回收处理中心，新建3个初级回收代理点，即h=3。拟在市区的c= 4个区域中建立2个集中回收处理中心，即g=2。有s=1个拆解中心，i=1个检测中心，d=1个废品处理点和r=1个回收再利用中心。部分数据如表1所示。

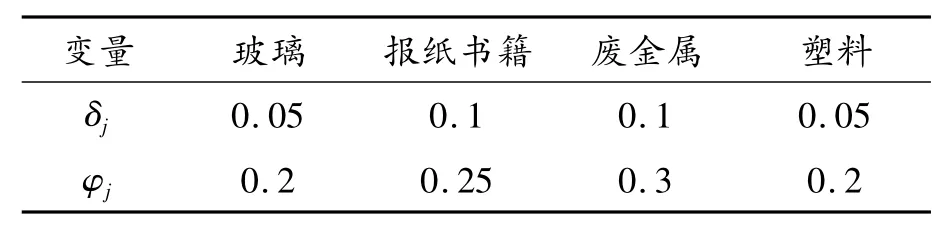
表1 j的损耗率

利用Visual C++6.0开发基于Benders分解方法的计算软件包，用于求解上述问题。结果见表2。该模型涉及的数据较多，但在所有数据的支持下可知该模型有效且实用。

表2 新建回收处理中心并投入运营的费用

3 结束语

本文针对农村地区废弃物堆积的状况，为农村废弃物的回收建立了一个混合整数线性模型，并利用Benders算法求解，最后通过算例验证了模型的有效性。通过对模型的求解，确定了多产品、侧重于回收、有条件限制时各初级回收代理中心和集中回收处理中心的选址以及物流量的合理分配。

新建立的回收及处理中心的处理能力有限，而逆向网络回收物流因环境等因素的影响具有高度的不确定性，因此还需进一步研究上述条件下多产品回收逆向物流网络的优化设计。

［1］欧阳建军.农业废弃物逆向物流现状分析与发展对策研究［J］.商业现代化，2009，18:66－67.

［2］王新利.论农村逆向物流及其网络模型设计［J］.中国流通经济，2007(2):19－21.

［3］董景峰，王刚，吕民，等.产品回收多级逆向物流网络优化设计模型［J］.计算机集成制造系统，2008，14 (1):33－38.

［4］马祖军，代颖.产品回收逆向物流网络优化设计模型［J］.管理工程学，2005，19(4):114－117.

［5］陈义华，许庆春.基于Markov过程的逆向物流回收量预测［J］.重庆理工大学学报:自然科学版，2012，26 (1):108－111.

［6］Benders JF.Partitioning procedures for solving mixed variables Programming problems［J］.Numersiche Mathematik，1962，4(1):238－252.

(责任编辑 刘舸)

Optim ization Model for Reverse Logistics Network for Rural Solid Wastes

CHAIYue－zhen
(College for Mathematics and Statistics，Chongqing University，Chongqing 401331，China)

In order to reduce waste and gain recycling benefits，this article designed a reverse logistics networks for the rural solid waste recycling.Based on mixed integer linear programming method formulti－commodity，we focused on recycling，capacitated optimization design model.The objective is tominimize the sum of investment and operating costs and processing costs.The primary recycling agency locations and the recycling center are determined too.Using Benders algorithm to solve the model，the validity of themodel is verified by an example.

rural area;multi－commodity;capacitated;reverse logistics;mixed integer liner programming

O21

A

1674－8425(2014)09－0143－04

10.3969/j.issn.1674－8425(z).2014.09.030

2013－11－29

柴月珍(1984—)，女，河南人，硕士研究生，主要从事物流网络优化研究。

柴月珍.农村固体废弃物回收逆向物流网络优化［J］.重庆理工大学学报:自然科学版，2014(9):143－146.

format:CHAIYue－zhen.Optimization Model for Reverse Logistics Network for Rural Solid Wastes［J］.Journal of Chongqing University of Technology:Natural Science，2014(9):143－146.