遗传神经网络在室内环境热舒适度融合评价中的应用研究

胡晓倩，张莲，蒋东荣

(重庆理工大学电子信息与自动化学院，重庆 400054)

遗传神经网络在室内环境热舒适度融合评价中的应用研究

胡晓倩，张莲，蒋东荣

(重庆理工大学电子信息与自动化学院，重庆 400054)

针对室内环境热舒适度评价，为解决影响PMV(predicted mean vote)指标的各因素之间复杂的非线性关系，利用核主成分分析KPCA(kernel principal component analysis)的非线性映射方法，对输入变量进行特征提取，以消除各因素之间的非线性关系，然后利用遗传神经网络GNN(genetic neural network)进行融合评价。对比GNN和KPCA+GNN的仿真评价结果可知:对于该室内热环境舒适度融合评价问题，KPCA能提取影响PMV指标的主要因素成分，KPCA+ GNN是有效的预测方法。

核主成分分析;遗传神经网络;热舒适度

随着居住水平的提高，人们越来越关心所处环境舒适与否，周围环境的热舒适度直接对人的感觉器官和心理舒适产生影响。影响人体热舒适度的因素涉及多指标、多属性的不确定性，且各因素之间存在耦合特性。目前，国际上较通用的热舒适度指标是预测平均投票值PMV(predicted mean vote)［1］。PMV指标综合考虑了环境因素和人的因素，包括人体活动情况(新陈代谢率)、衣着情况(服装、热阻)、空气温度、空气相对湿度、空气流速、平均辐射温度6个因素。

由于PMV指标的6个因素之间存在非常复杂的非线性关系，因此在进行室内环境热舒适度的预测和评价时，必须考虑除去各变量之间的高阶非线性相关性，提取完备、有效的样本特征。Scholkopf等提出的核主成分分析KPCA(kernel principal component analysis)［2］是非线性特征提取的有效方法，可用于故障诊断与辨识中，具有很强的应用价值。因此，本文采用KPCA的非线性映射方法，对输入变量即PMV指标的影响因素进行特征提取，以消除这6个因素之间的非线性关系;再利用遗传神经网络GNN(genetic neural network)进行融合评价，最终提取出影响PMV指标的主要因子，提高室内环境热舒适度的预测精度。

1 基于PMV指标方程的样本数据获取

一个良好的神经网络模型的性能在很大程度上取决于样本数据的选取。由于本文选择PMV指标作为室内环境热舒适度的评价指标，因此建立热舒适度神经网络评价模型所需要的样本数据必须基于PMV指标方程进行计算，这样才能最真实、准确地反映室内环境的热舒适度。本文根据文献［1］给出的PMV指标方程(1)，通过在Matlab中编写PMV计算程序求得PMV值。

式(1)～(4)中:M表示人体的能量代谢率，W/m2，决定人体的活动量大小;W表示人体所做的机械功，人体不同活动强度下对外输出的机械效率(一般取值为0)，W/m2;Pa表示人体周围空气的水蒸气分压力，Pa;ta表示人体周围环境的空气温度，℃;tmrt表示房间内的平均辐射温度，℃;Icl表示服装热阻，m2·K/W;fcl表示穿衣表面系数，为人体着装后实际表面积Fcl与其裸身人体表面积之比，与服装热阻有关，即:fcl=FclFD;tcl表示衣服的外表面温度，℃;hc表示表面传热系数，W/(m2·K);Va表示空气流速，m/s。

根据式(5)计算出预测不满意百分比PPD (predicted percent dissatisfied)值，构成本研究的样本数据。

选择神经网络各节点的激活函数为Sigmoid函数，考虑到Sigmoid函数在值域［0，0.1］和［0.9，1.0］区间的曲线变化极为平坦，为提高网络的训练速度，将各输入样本数据归一化至［0.1，0.9］区间，采用最小－最大标准化处理方法。

通过计算，共得到170组PMV和PPD值的样本数据，采取等间隔的方式从中抽取数据。其中85组样本数据用于训练所建立的神经网络，另外85组则用于测试神经网络性能，以确保预测能力。

2 融合神经网络模型的建立

本文采用3层BP网络结构，输入层节点数为6，分别对应PMV指标的6个影响因素。由于需要求取热舒适度指标PMV值和预测不满意百分比PPD值，故输出层节点数确定为2个。考虑到隐含层节点数的选取是网络训练成败与否的关键，为确定合理的隐含层节点数，本文采用结合试凑和经验公式的优化选择方法，先根据经验公式选择2n+1=13个(n为输入层节点数)，再左右偏差3，初步确定隐含层节点数范围为［10，16］。分别进行相关训练后，再进行收敛性及收敛速度试验。通过多次试验比较，最终确定所需要的最优的隐含层节点数为15。所建立的室内环境热舒适度的融合神经网络模型见图1。其中，隐含层的传递函数采用sigmoid型函数，输出层采用线性传递函数pureline型函数［2］。

图1 室内环境热舒适度的融合神经网络模型

本文利用遗传算法的全局优化搜索能力，对BP神经网络的初始权值和阈值进行寻优。然而，遗传算法的局部搜索能力较弱，一般只能搜索到次优解而不是最优解，而非线性规划的梯度下降法则具有极强的局部搜索能力及很高的迭代寻优效率。为寻找真正的全局最优解，避免局部极小值，将搜索范围缩小后，按照网络性能参数的负梯度方向调整BP网络的权值和阈值，以得到全局最优解，同时提高网络的训练速度［4－6］。

利用遗传算法优化BP网络初始权值和阈值的方法和步骤如下［7］:

步骤1初始化种群P，进行种群规模n、交叉概率Pc、变异概率Pm的初始化。首先采用实数进行编码，根据实际应用选择数值大小，取初始种群n=100。为优化种群的进化，采用可变交叉概率，在遗传算法的初期使用大的交叉概率Pc加剧种群的变化，以更快地寻找优良种群所处的区域;随着进化的进行，逐渐减小交叉概率，避免过大的交叉概率破坏适应度较高的个体，同时避免过小的交叉概率降低搜索速度。取Pc=0.4 n+0.5，n为当前的进化代数;变异概率Pm=0.02;遗传代数取为200。

步骤2计算出各个体评价函数，并将其排序，按式(6)给出的概率值选择网络个体。

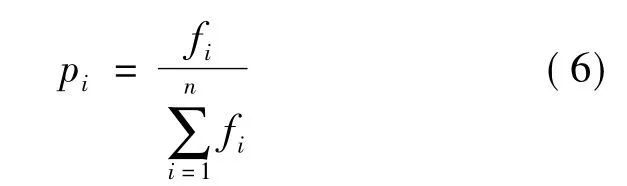
其中:fi为第i个个体的适配值，用误差平方和E来衡量，即:

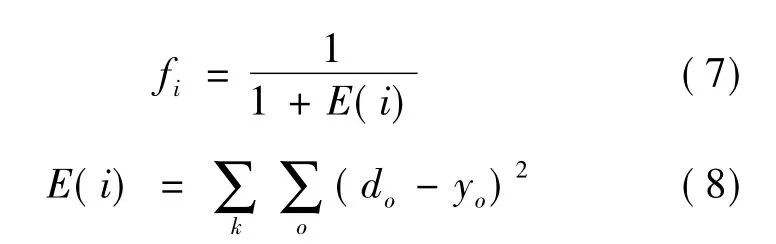
其中:i为染色体个数，i=1，2，…，100;o为输出层的节点数，o=1，2;k为学习样本数，k=1，2，…，85;y为网络的实际输出;d为期望输出。

步骤3以交叉概率Pc对个体Gi和Gi+1进行交叉操作，以产生新的个体G'i和G'i+1，没有进行交叉操作的个体则直接进行复制。

步骤4利用变异概率Pm突变产生Gj的新个体G'j。

步骤5将产生的新个体插入到种群P中，并计算新个体的评价函数。

步骤6根据预先设定的遗传代数200，判断遗传算法是否结束。若结束则转入步骤7;否则再次转入步骤2进入新一轮遗传操作，并计算误差平方和E。

步骤7将最终群体中的最优个体解码，得到优化后网络的初始连接权值和阈值。

整个遗传算法结束后，进入BP神经网络的运算。将遗传算法得到的最优个体解码作为BP网络的初始权值和阈值，然后利用BP算法进行学习，分为前馈计算和反向调节2个过程。学习样本经输入层送至隐含层，经隐含层节点的激励函数作用后，再把隐层节点的输出信号传播到输出层节点，经输出层处理后给出网络的输出值，这是信息前馈过程;然后，将网络输出值与学习样本的期望值相比较，其误差从输出层到隐含层再到输入层进行反向传播，逐层调节各连接权值和节点的阈值，这是误差反向调节过程。这2个过程反复进行多次，直到误差达到精度要求为止。BP算法学习规则的指导思想是:对网络权值和阈值的修正要沿着表现函数下降最快的方向——负梯度方向，即:

其中:ωk是当前的权值和阈值矩阵;gk是当前表现函数的梯度;αk是学习速率。

3 输入变量的特征提取

为解决影响PMV指标的各因素之间复杂的非线性关系，本文基于KPCA对输入变量进行相关特征提取，再利用神经网络进行融合，最终提取出影响PMV指标的主要因素成分，从而提高样本质量和预测精度。

3.1 核主成分分析KPCA

核主成分分析法KPCA的分析基础是核函数方法。核函数方法的基本原理如图2所示，它将原始空间S中的数据X通过选择适当的非线性函数Φ映射到高维特征空间Η中。由于S与Η具有同构性，故原始空间S中的非线性问题可转换成特征空间Η中的线性问题进行分析和解决。如何确定恰当的非线性变换函数Φ是核函数方法的关键。由Mercer定理可知，通过定义任意正定对称的核函数K(x，x)，如式(9)所示，均可将原始空间中的非线性问题恰好转化为特征空间中仅涉及内积运算的线性运算［3］。

图2 函数Φ将原始空间S中的数据映射到特征空间Η中

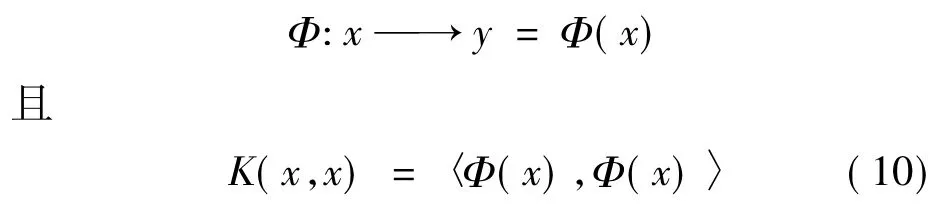
假设Φ是非线性变换函数，令其中:x为原始空间S中的数据;y为特征空间Η中的数据;Φ为所选择的隐式的非线性变换函数; K为正定对称的核函数。

KPCA方法本质上是利用核映射的原理，将原始空间中的非线性数据映射到高维特征空间，再在高维特征空间对映射后的数据实现线性主成分分析PCA，因此能实现样本空间的非线性特征的提取［3］，可用于非线性系统的故障检测与预测。

3.2 KPCA进行特征提取的实现过程

经过标准化处理的样本集为{x1，x2，…，xm}，E{x1，x2，…，xm}=0。其中xi∈Rl，l为样本数量，m为样本维数，形成l×m维的输入矩阵。通过非线性变换Φ(X)，将样本集映射到高维特征空间Η中。Φ(X)的协方差矩阵为

其特征向量vi就是原始样本空间xi在特征空间Φ (xj)上的主元方向，满足

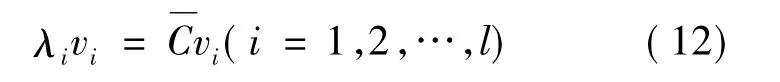
其中:特征值λi≥0，并按从大到小的顺序排列(λ1≥λ2≥…≥λl)。

将每个样本xj，j=1，2，…，l，变换为Φ(xj)后，与式(11)内积，得

由于vi是Φ(xi)的线性组合，于是存在αi，i=1，2，…，l，满足

其中:j=1，2，…，l，αi(j)表示向量αi的第j个元素。

将式(10)和(13)代入式(12)，得

其中，j=1，2，…，l。

在特征空间中，满足Mercer定理的核函数K对应非线性函数的内积运算，即

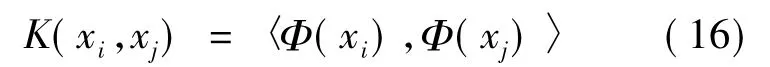
将核矩阵进行中心化处理。根据式(14)，式(13)可转换为

其中，α=[α1…αl]为特征向量。

在特征空间中，特征向量α=[α1…αl]经过线性主成分分析PCA特征提取后，将得到满足主元贡献率的前k个主元向量α=[α1…αk]，以及相应的主元特征向量v=[v1…vk]。因此，通过Φ(X)在主元方向V上的投影，可得到原始空间X的主元向量=(x1，x2，…，xk)，即

其中:p=1，2，…，k，αp(i)为特征向量αp中的第i个元素;vp为v的第p个特征向量;K( xi，x)为核函数［4－6］。

通过以上步骤，实现了从X∈Rl×n到∈Rl×k的非线性特征提取。

3.3 基于KPCA的特征提取结果

根据累计贡献率CPV(cumulative percent variance)确定主元数量k，KPCA的核函数选为高斯核函数，核函数宽度取为0.1。KPCA特征提取的结果见表1，取CPV为90%时的主元数为最终的特征提取主元数，即KPCA为71个主元。

表1 KPCA特征提取结果

4 仿真结果分析

直接利用遗传神经网络GNN和BP网络的仿真结果，以及利用KPCA进行特征提取，然后分别利用遗传神经网络和BP网络进行融合的Matlab仿真结果见图3～5。

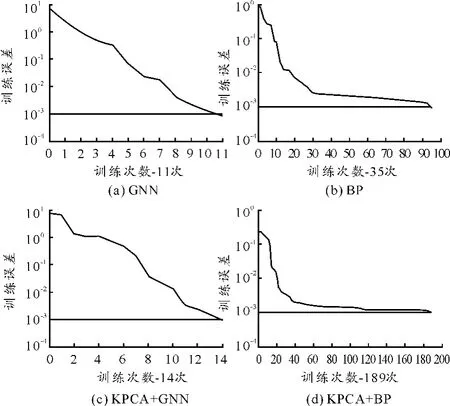
图3 训练误差曲线对比

由图3可知:KPCA+BP网络经过189次训练达到精度要求0.001，而KPCA+GNN网络仅经过14次训练就达到了同样的精度要求，验证了将遗传算法与神经网络结合可优化网络的权值和阈值，极大地提高了网络的收敛速度。但KPCA+ BP网络和KPCA+GNN的训练次数均多于BP网络和遗传神经网络，说明KPCA反而增加了该问题计算的复杂度，也验证了经KPCA特征提取后的维数一般高于原始输入向量的维数。

对比图4和5可知:经KPCA特征提取后的神经网络的预测误差明显小于未经特征提取的BP网络和遗传神经网络的预测误差。这说明KPCA方法能剔除变量中的高阶非线性相关信息，提取出变量中的主要成分。虽然计算的复杂度有所增加，同时导致了网络收敛速度的减慢，但相较于未经特征提取的神经网络，基于KPCA方法的网络预测精度明显提高。Matlab仿真结果表明:对于该室内环境热舒适度融合评价问题，KPCA+GNN是有效的预测方法。

图4 GNN和BP预测PMV值及PPD值实际输出与期望输出绝对误差曲线

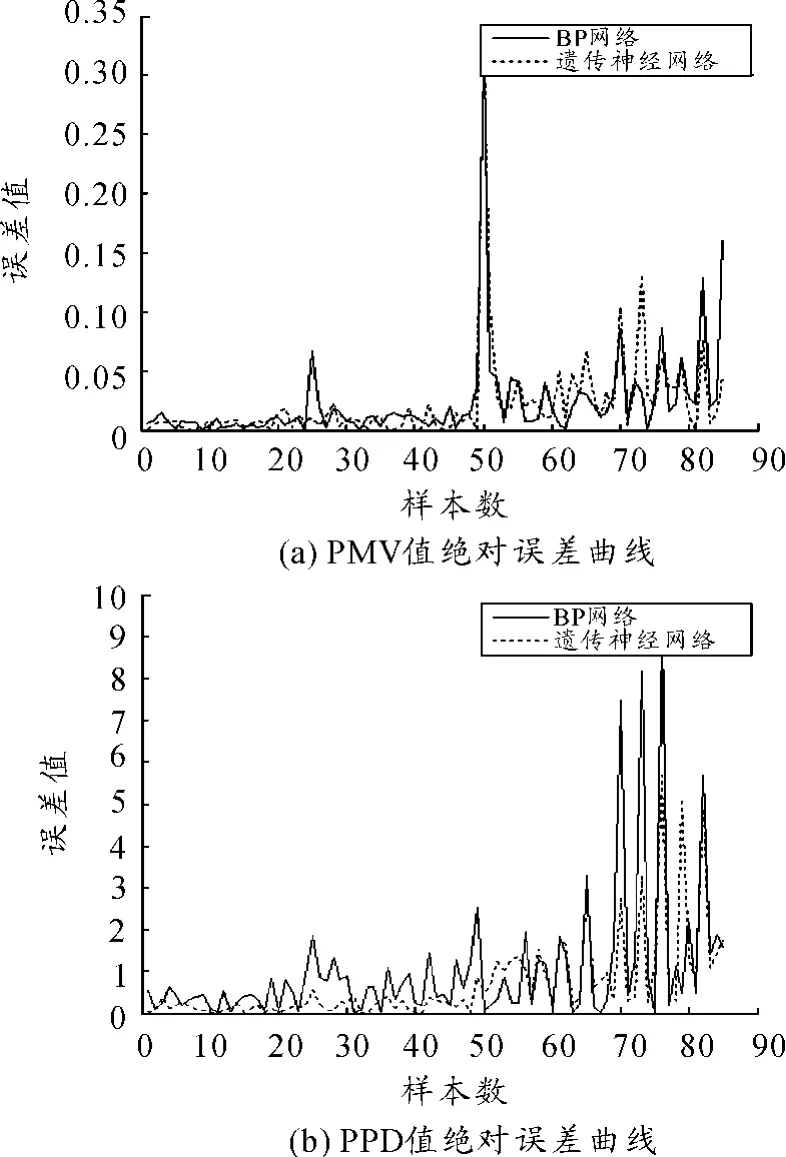
图5 基于KPCA的预测PMV及PPD值实际输出与期望输出的绝对误差曲线

5 结束语

针对室内环境热舒适度PMV的评价，本文建立了基于核主成分分析(KPCA)的遗传神经网络融合模型。首先利用KPCA的非线性映射方法对输入变量进行特征提取，以消除PMV指标各因素之间的非线性关系。然后建立遗传神经网络GNN进行融合评价，综合遗传算法的全局优化搜索能力和梯度下降法的局部搜索能力及很高的迭代寻优效率，优化BP神经网络的权值和阈值，寻找真正的全局最优解，并提高网络训练速度。对比GNN和KPCA+GNN的仿真评价结果可知:对于室内环境热舒适度融合评价问题，KPCA能提取出影响PMV指标的主要因素成分，KPCA+GNN是有效的预测方法。

［1］曾光，田永铮，赵华，等.环境因素及综合因素对PMV指标的影响分析［J］.建筑节能，2007，35(193):11－16.

［2］王泽平.基于GA－BP与多隐层BP网络模型的水质预测及比较分析［J］.水资源与水工程学报，2013，24 (3):154－160.

［3］吴洪艳，黄道平.基于特征向量提取的核主元分析法［J］.计算机科学，2009，36(7):185－255.

［4］闫建华，宇仁德，汪洋.基于主成分分析的道路交通事故预测［J］.交通与安全，2009(204):86－90.

［5］李岩，王东风，韩璞.基于核主元分析和多级神经网络集成的汽轮机故障诊断［J］.电力科学与工程，2009，25(6):67－71.

［6］薄翠梅，王执铨，张广明.基于KPCA－PNN的复杂工业过程集成故障辨识方法［J］.信息与控制，2009，38 (1):98－104.

［7］张方方.室内环境多信息融合算法的研究［D］.重庆:重庆理工大学，2010.

(责任编辑 杨黎丽)

Research on Genetic Neural Network Fusion for Evaluation of Indoor Thermal Com fort Degree

HU Xiao－qian，ZHANG Lian，JIANG Dong－rong
(School of Electronic Information and Automation，Chongqing University of Technology，Chongqing 400054，China)

Aiming at the evaluation of indoor thermal comfort degree，and in order to solve the complex nonlinear relationship between the influencing factors of PMV(Predicted Mean Vote)index，the non－linearmapping approach of KPCA(kernel principal component analysis)is introduced to extract characteristics of input variables and to eliminate the nonlinear relationship between variables.Then based on GNN(genetic neural network)，the fusion evaluation of indoor thermal comfort degree is implemented.By the comparison of GNN and KPCA+GNN，the simulative results show that:for the fusion evaluation of indoor thermal comfort degree，KPCA can extract the main influencing factors of PMV index，and KPCA+GNN is an effective forecasting approach with high accuracy.

KPCA;genetic neural network;heat comfort degree

TP183

A

1674－8425(2014)09－0102－06

10.3969/j.issn.1674－8425(z).2014.09.022

2014－04－08

重庆市教委科技计划项目(KJ120803)

胡晓倩(1977—)，女，硕士，讲师，主要从事控制理论及电气工程方面研究。

胡晓倩，张莲，蒋东荣.遗传神经网络在室内环境热舒适度融合评价中的应用研究［J］.重庆理工大学学报:自然科学版，2014(9):102－107.

format:HU Xiao－qian，ZHANG Lian，JIANG Dong－rong.Research on Genetic Neural Network Fusion for Evaluation of Indoor Thermal ComfortDegree［J］.Journal of Chongqing University of Technology:Natural Science，2014(9):102－107.