一种改进的毫米波图像超分辨率重建算法
徐蕊娟
(电子科技大学光电信息学院,四川成都610054)
一种改进的毫米波图像超分辨率重建算法
徐蕊娟
(电子科技大学光电信息学院,四川成都610054)
针对毫米波成像时,由于天线孔径受限使得获取的图像空间分辨率很低、高频信息损失严重的问题,提出一种改进的非凸集投影超分辨算法。该算法以非凸集阈值收缩迭代算法(Non-convex Shrinking Iteration,NCSHI)为基础,采用具有平移不变特性的双树复数小波作为稀疏基,引入了两步迭代过程,有效地利用了前两次的迭代信息。实验仿真结果表明,该算法有效地改善了伪吉布斯效应,收敛速度更快,具有良好的超分辨性能。
毫米波成像;非凸集投影;超分辨;图像重建
1 毫米波成像
毫米波成像机理类似于红外成像[1-2],其成像技术就是结合不同物体间辐射强度的差异,通过探测物体自身的毫米波辐射能量实现成像。但由于天线馈源尺寸的限制以及衍射受限效应,使得获取的图像分辨率很低。为了有效恢复衍射受限截止频率之外的图像高频信息,可以从信号处理的角度进行处理,即应用超分辨算法[3]来恢复更多被滤掉的高频信息。
在毫米波成像领域,目前提出了许多具有实用价值的超分辨算法。主要有最大后验(MAP)算法[4]、正交匹配追踪(OMP)算法[5]、凸集投影(POCS)算法[6]等。近年来,有学者提出了一种快速迭代算法[7],即两步迭代收缩算法(Two-step Iterative Shrinkage/Threshold,TwIST)。该算法由前两次的迭代结果得到新的估计值,能够更快速更有效地得到目标解。
为了得到更好的图像复原结果,可以有效地加入图像的稀疏先验信息,如近年来新兴的压缩感知(Compressed Sensing,CS)理论[8]。一般的重建算法通常选择具有三个方向的正交小波基作为图像的稀疏基,而正交小波基具有一定的局限性,不仅方向选择性差,而且不具备平移不变性,重构的图像会产生伪吉布斯效应。针对这一缺陷,本文选择了具有平移不变特性的双树复数小波[9]作为稀疏基对原始信号稀疏表示,在NCSHI算法基础上引入了两步迭代,有效地改善了重建图像质量。
2 超分辨算法数学模型
毫米波成像衍射受限系统如图1所示,其过程主要为:场景目标辐射能量,天线系统通过检测接收物体的亮温分布,再进行一系列的信号处理,如对接收到的信号进行放大、滤波、检波等,最后进行超分辨复原得到原始场景图像。其数学模型可以抽象为
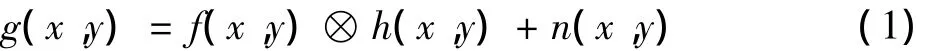
式中:g(x,y)表示观测到的图像;f(x,y)和h(x,y)分别为原始场景图像和系统的点扩散函数;n(x,y)是系统的加性噪声。在实际的建模过程中,如果忽略通道不一致性以及多波束的非均匀性影响因子,可以得到图1的成像模型。

图1 毫米波成像模型
由该模型可以看出,毫米波成像系统前端类似于一个低通滤波器,在成像过程中,空间频谱的高频分量被滤除。因此,对所得到的低质量图像进行超分辨复原的目的即利用毫米波图像的稀疏先验信息,尽可能多地恢复被滤除的截止频率之外的频谱分量,从而得到与原始图像误差量最小的一个估计值。
依据式(1)中的测量模型,由于系统中存在不可避免的噪声影响,所以实际的测量为

式中:Φ为测量矩阵,因为毫米波图像具有一定的稀疏特性,故式(2)中x是稀疏的。对于给定的参数ε,可以得到目标优化函数

其中,p范数的定义为

式中:参数ε可以根据x的稀疏性和解对于约束条件的满足程度进行相应的调整。
3 基于非凸集阈值收缩迭代图像复原方法
非凸集投影(NCSHI)算法[10]是以经典的空域重建算法凸集投影(POCS)算法为基础,通过不断地向一个p(p<1)范数球(lp-ball)进行近似正交投影得到的。该算法在每一次迭代过程中,相比于POCS算法,其阈值并不是固定不变的,而是自适应地根据前一次的迭代结果进行阈值计算,从而提高了重建精度以及算法的收敛速度。
非凸集投影算法是以任意一个起始点为初始值,通过不断地向超平面H和一个p(p<1)范数球进行投影。对于长度为N的信号x来说,对其目标优化函数求变分,可以得到变分方程[11]

该算法主要的迭代步骤如下[10]:
步骤1:任意选择一个起始点,向H超平面进行正交投影
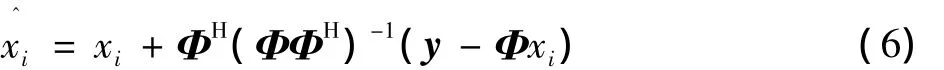
步骤2:通过自适应软阈值过程向非凸集近似正交投影

式中:Sε为当p<1时的软阈值过程,具体操作如下

式中:i=1,2,…,N。
由上述可以看出,非凸集投影算法的阈值过程是自适应的,并且由式(7)可知它是向一个非凸集投影。因此具有更好的收敛速度和重建性能。
4 改进的非凸集投影算法INCSHI
虽然NCSHI算法在投影过程中,其阈值计算是自适应的,但是还没有更充分地利用前面的迭代结果,其对图像的超分辨重建性能有限。改进的INCSHI算法选择具有平移不变特性的双树复数小波基作为图像的稀疏基,并引入了两步迭代过程,从而更多地利用了前两次的迭代信息,能够以更高的精度估计出原始信号。
该算法的核心就是在自适应阈值的基础上,加入了两步迭代过程,即利用前两次的迭代结果来估计当前的信号值。两步迭代收缩(TwIST)算法的更新过程如下[7]
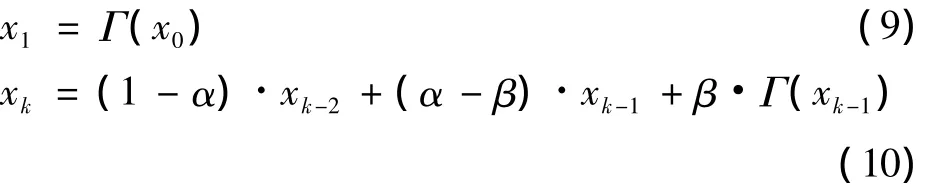
式中:x0表示迭代的初值,且k≥2;Γ(x)为降噪处理函数,α和β是决定该算法收敛速度的因子。本文中选择这两个参数值分别为
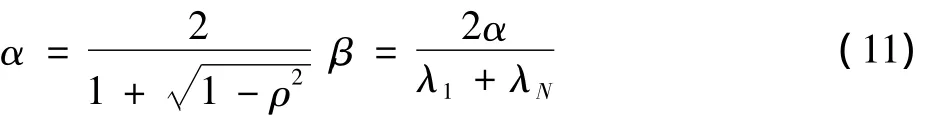
由于毫米波图像具有稀疏性,可以用稀疏基来表示。本文选取双树复数小波基作为图像的稀疏基,假设基为Ψ =(Ψ1,Ψ2,Ψ3,…,ΨN),则原始信号f可以表示为

进而得到以下投影迭代自适应阈值迭代公式
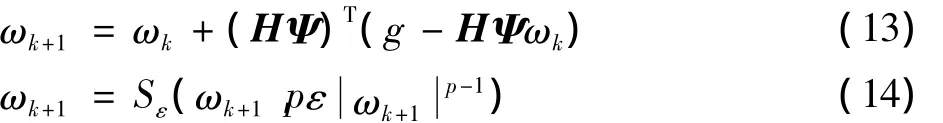
式中:H表示测量过程中的观测算子;ω为原始信号f在稀疏基Ψ下的表示系数;软阈值过程Sε同式(8)。再利用式(10)进行两步迭代,得到
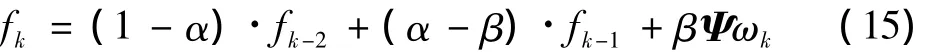
最后利用图像的非负先验信息,得到最终值

其中

流程图见图2。
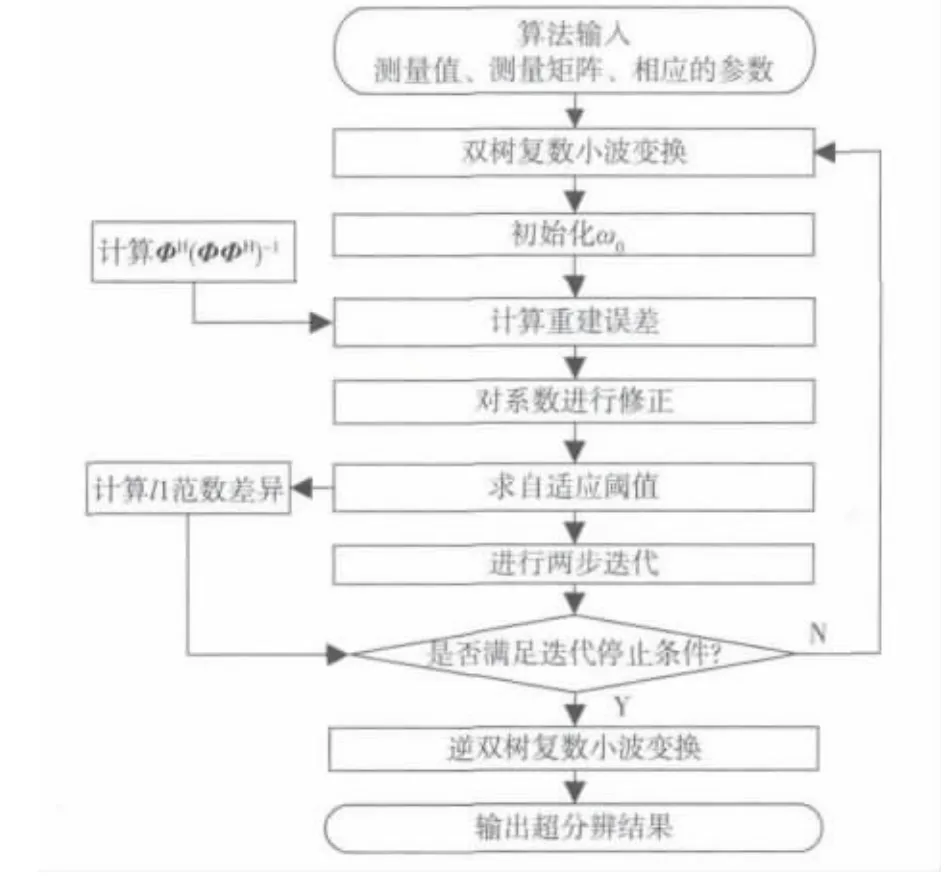
图2 INCSHI算法流程图
5 实验仿真结果与分析
为了验证INCSHI算法的有效性,本文采用一幅实际的毫米波图像(图3b),它的光学图像为图3a。分别用NCSHI算法和INCSHI算法进行仿真,将图3b作为原始的场景信号进行输入。为了更充分地说明比较效果,在实验中采用相同的参数(如迭代步长、迭代停止条件等),迭代次数为30次。超分辨重构的图像及其相对应的频谱如图4所示。通过图4可以看出,NCSHI算法和INCSHI算法都具有明显的超分辨能力,但在相同的迭代次数下,INCSHI算法相比NCSHI要更平滑一些。由频谱图可以看出,INCSHI算法更有效地抑制了高频噪声,同时具有更好的频谱外推能力。

图3 原始光学图像和毫米波图像
目前,有很多评估超分辨算法性能的客观评价准则,这里采用最常用的评估准则均方误差(MSE)

图4 NCSHI与INCSHI恢复图像及其频谱

式中:x(i,j)和x1(i,j)分别表示原始信号与重建的信号,这两种算法迭代次数与MSE之间的关系如图5所示。由图可以看出,当两种算法迭代次数相同时,INCSHI算法的MSE值要小于NCSHI算法的MSE值,并且衰减速度要快些。由此可以得出结论,在同一迭代次数条件下,本文算法的超分辨能力要优于NCSHI算法,而且收敛速度相对较快,从而可以在更短的时间内达到较好的重建效果。

图5 均方误差测量
6 结束语
本文从非凸集投影算法出发,详细分析了其算法原理。在迭代过程中引入了两步迭代步骤,并结合具有平移不变性的双树复数小波基对图像进行稀疏表示。从实验结果可以看出,本文的算法进一步改善了超分辨重建性能,同时提高了算法的收敛速度,因此,可以作为一种更有效的超分辨算法。
[1]LIL,YANG J.Method of passive MMW image detection and identification for close target[J].Journal of Infrared,Millimeter,and Terahertz Waves,2011,32(1):102-115.
[2]YUJIRI L,SHOUCRIM,MOFFA P.Passive millimeter-wave imaging[J].IEEEMicrowave Magazine,2003,4(9):39-50.
[3]LETTINGTON A,YALLOP R,DENNISD.Review of super-resolution techniques for passivemillimeter-wave imaging[C]//Proc.SPIE Infrared and Passive Millimeter-Wave Imaging Systems:Design,Analysis,Modeling,and Testing.Bellingham,USA:SPIE Press,2002:230-239.
[4]HUNT B,SEMENTILLIP.Description of a poisson imagery super-resolution algorithm[J].Astronomical Data Analysis Software and System I,1992(25):196-199.
[5]TROPP J,GILBERTA.Signal recovery from random measurement via orthogonalmatching pursuit[J].IEEE Trans.Information Theory,2007,53 (12):4655-4666.
[6]ELAD M,FEUER A.Restoration of a single super resolution image from several blurred,noisy and under-sampled measured images[J].IEEE Trans.Image Processing,1997,6(12):1646-1658.
[7]JOSEM,BIOUCASD,MARIO A,et al.A new TwIST:two-step iterative image,processing,shrinkage/thresholding algorithms for image restoration[J].IEEE Trans.Image Processing,2007,16(12):2992-3004.
[8]BARANIUK R.A lecture on compressive sensing[J].IEEE Signal Processing Magazine,2007,24(4):118-121.
[9]KINCSBURY N.The dual-tree complex wavelet transform:a new efficient tool for image restoration and enhancement[EB/OL].[2013-06-02].http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1. 47.5647.
[10]ZHOU Changlin,XIONG Jintao,LILiangchao.Research on passivemillimeter wave imaging using compressed sensing architecture[C]//Proc. ICACTE 2010.Chengdu:IEEE Press,2010:479-483.
[11]DAUBECHIES I,DEFRISE M,DE MOL C.An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Comm.Pure Appl.Math.,2004,57(11):1413-1457.
M odified M ethod of Passive M illimeter-wave Imaging Super-resolution Reconstruction
XU Ruijuan
(School of Optoelectronic Information,University of Electronic Science and Technology of China,Chengdu 610054,China)
To solve the problem of low resolution images caused by the low-pass effect of passive millimeter wave imaging system,a modified method based on the non-convex shrinking iteration(NCSHI)algorithm for reconstruction process is put forward in this paper.This paper presentsan algorithm using dual-tree complex wavelet transform and two-step iterative shrinkage,which makes effective use of the previous estimations in order to gain amore accurate value.Experimental results demonstrate this algorithm can overcome the pseudo-Gibbs effect,has better super-resolution performance and its convergence rate is faster.
passivemillimeter-wave imaging;non-convex shrinking iteration;super-resolution;image restoration
TP391
A
徐蕊娟(1987— ),女,硕士生,主研无源毫米波超分辨成像。
�� 雯
2013-07-24
【本文献信息】徐蕊娟.一种改进的毫米波图像超分辨率重建算法[J].电视技术,2014,38(13).

