永磁直线同步电机的模糊内模速度控制

方 涛，陈其工，陆华才

（安徽工程大学 安徽省检测技术与节能装置重点实验室，安徽 芜湖 241000）

传统的工业生产过程中，若要求被控对象执行直线形式的运动，很多驱动装置及系统都需要使用旋转电机＋中间转换器件（例如链条、传动带、齿条等）的形式，将旋转运动形式转换为直线运动的形式.由于这些中间环节才存在，会产生较大的转动惯量、弹性形变和反向间隙，进而会在运动过程中产生滞后、摩擦、噪声、振动和磨损等种种问题，日积月累，导致机器精度不高、寿命变短，且整体装置的体积大、精度低、效率低.永磁直线同步电机（Permanent Magnet Linear Synchronous Motor，PMLSM）具有推力大、电气时间常数小、损耗低、响应速度快等优点，可以从根本上消除传统的直线运动系统带来的弊端，因此，PMLSM在高速精度数控系统中有广阔的应用前景［1］.然而，并非不存在其他问题，如在PMLSM驱动时，由于采用零传动技术，系统参数会有摄动，加上负载扰动等一些不确定因素的影响，又加上没有任何中间环节的缓冲，控制难度很大，从而导致永磁直线同步电机运行不稳定.

内模控制理论由Garcia和Morari在1982年正式提出，以其简单、跟踪调节性能好、鲁棒性强、可消除不可测干扰等优点被控制界所重视.近年来，学者提出很多直线电机的控制策略（如模型参考自适应控制、自校正控制、H∞鲁棒控制等），都具有一定价值，但算法过于复杂［2］.本文针对永磁直线同步电机运行中一些不确定因素的影响，将内模控制与模糊控制相结合，利用模糊控制理论实现控制器参数实时调整.仿真实验表明，设计的控制器性能优于常规的反馈控制，可使系统具有较好的快速性、稳定性和鲁棒性.

1 永磁同步直线电机的数学模型

忽略端部效应和磁路中铁心的磁饱和，不计铁心的涡流损耗和磁滞损耗情况下，可根据直线电机的d－q模型的电压平衡方程和运动学平衡方程建立永磁同步直线电机的数学模型［3］.

d轴电压平衡方程：

q轴电压平衡方程：

电磁推力方程：

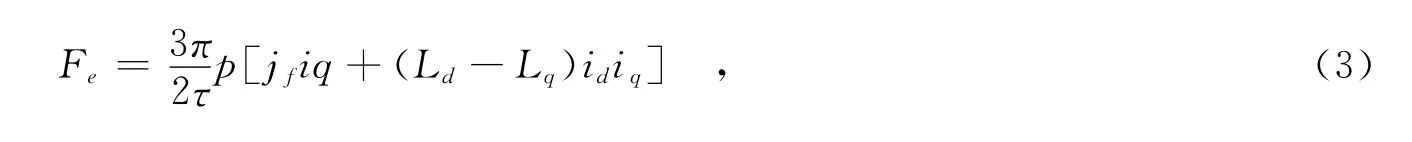
机械运动平衡方程：

其中id、iq为d、q轴电流；ud、uq为d、q轴电压；Rs为初级绕组电阻；Ld、Lq为d、q轴电感；jf为永磁体磁链；w＝πv/τ，v为动子线速度，Fload为负载；τ为极距；m为动子质量；D为粘性摩擦系数；Fe为电磁推力；p为极对数（为简化p取1）.当采用id＝0的磁场定向控制策略时，模型可简化为［4］：

方程中，状态变量x＝［iqv］T，输入变量u＝［uq］，输出变量y＝v，d＝－Fload/m是负载扰动项，

根据式（5）且负载为零的情况下，可得出速度v关于电流iq的传递函数为G＝Kf/（ms＋D）.

在PMLSM闭环控制系统中，为了使速度控制器的设计难度降低，可以将逆变器看作广义的“被控对象”，将电流环内的环节看作一个整体，由于电磁时间常数远小于机械时间常数，故电流环响应速度远快于速度环响应速度，所以可将系统的电流环近似简化为传递函数为1的环节［5］.由以上分析可得PMLSM控制系统如图1所示.

2 内模控制器设计

内模控制（Internal Model Control，简称IMC）是一种基于过程数学模型进行控制器设计的新型控制策略［6］，其系统的结构框图如图2所示.其中，Gp为被控对象，Gm为被控对象的数学模型，即内部模型，GIMC为内模控制器，R、Y、F、E分别是系统的输入、输出、扰动和误差.

根据内模控制的性质可知，当模型无误差即Gp＝Gm，只需Gm和GIMC都是稳定的，便可以保证内模控制系统的闭环稳定.在这种情况下，若存在模型的逆模，即可设计内模控制器GIMC＝G－1p，从而实现理想控制.在现实设计中，为了使GIMC可实现，且可调整，故需在内模控制器中加入低通滤波器f（s），其基本形式为f（s）＝1/（lS＋1）n，其中参数n为逆模的型.由上可知，GIMC＝G－1p（s）f（s）.

内模控制系统的等效结构框图如图3所示，其由图2等效而来的.其中，GC反馈控制器，两种结构之间的变换关系如：

根据图1简化的速度控制系统设计内模控制器如下：

由GIMC和GC的转换关系，即式（6）得

由（10）式可知，GC具有PI控制器的结构，其中l是唯一可调整的参数.

图1 PMSM速度控制系统简化图

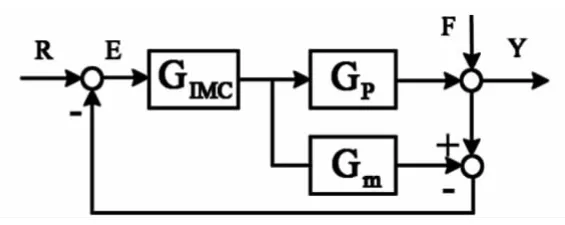
图2 内模控制系统结构框图

图3 内模控制系统等效结构框图

3 实时可调整l控制器设计

由GC的形式（10）可知，系统性能仅由l的大小决定.当l较小时，系统具有较好的快速性但鲁棒性较差；当l较大时，鲁棒性较好，但快速性较差［7］.故利用模糊控制的思想，将实时误差E和ED（即E的变化率）作为输入，经过模糊推理得出l，从而实现l根据误差和其变化率的实时可调整，即可兼顾系统的快速性和鲁棒性.

设定E的模糊集合A＝｛NB，NM，NS，ZE，PS，PM，PB｝分别代表负大、负中、负小、零、正小、正中、正大，其论域X＝｛－1，－0.6，－0.3，0，0.3，0.7，1｝.同样，设定ED的模糊集合B＝｛NB，NM，NS，ZE，PS，PM，PB｝代表同样的语言值，论域X＝｛－1，－0.6，－0.3，0，0.3，0.7，1｝.l的模糊集合为Z＝｛VS，

S，M，B，VB｝分别表示很小，小，中等，大，很大.论域Z＝｛1，2，3，4，5｝.该模糊控制器选取三角形隶属度函数.调整规则用“IFE＝AiANDED＝BjTHENl＝Cij”来描述，其中，i＝1，2，…，7；j＝1，2，…，7.其模糊规则如表1所示.运用Mamdani模糊推理规则，模糊判决采用重心法［8］.根据E和ED量化后的论域值通过模糊规则求得l的论域值，然后根据实际情况，乘以相应的比例因子就可以得到控制器的参数.

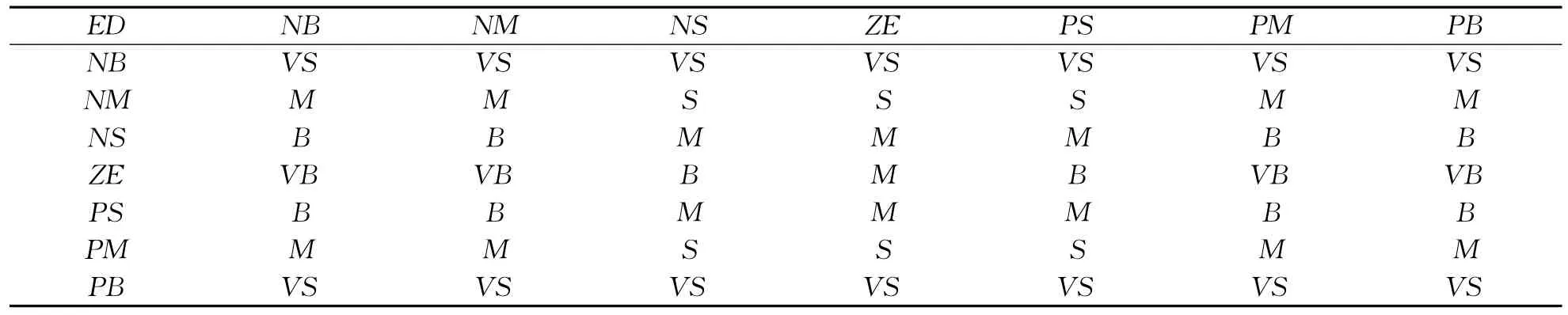
表1 模糊控制规则

4 仿真及实验结果分析

为了验证直线电机的模糊内模速度控制方法的正确性和有效性，利用Matlab/Simulink可搭建仿真模型如图4所示.其中，Fuzzy controller为在线实时调整l的模糊控制器，IMC controller为内模控制器，速度调节通过Fuzzy controller和IMC controller共同完成，电流调节为常规的PI调节.PMLSM的参数为：

R＝2.65Ω，Ld＝Lq＝2.67mH，m＝30kg，Kf＝89.25，D＝6N·s/m，Jf＝0.1Wb，τ＝16mm.

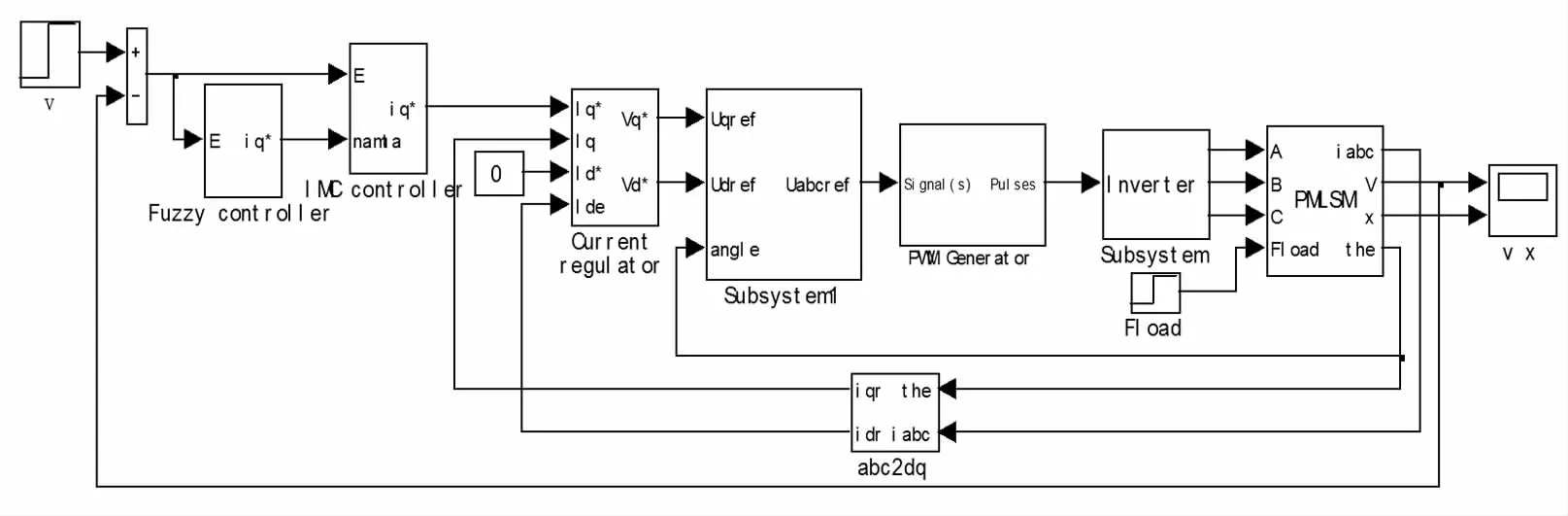
图4 系统仿真模型

为了检验设计系统速度响应的快速性和鲁棒性，同时还对常规的PI控制进行仿真（其中Kp＝32、KI＝290），对比验证设计系统的优越性，分别进行如下情况的仿真：

①无外界扰动且电机参数不变的情况下，永磁直线同步电机的速度响应如图5所示；②无外界扰动，但参数变为m＝50kg，D＝8N·s/m情况下，永磁直线同步电机的速度响应如图6所示；③参数变为m＝50kg，D＝8N·s/m，并在t＝1.4s时，加入100N的阶跃扰动的情况下，永磁直线同步电机的速度响应所图7所示.

由图5、图6和图7可知，当无外界扰动且电机参数不变的情况下，实时参数可调整内模控制和PI控制的速度阶跃响应的调整时间分别为0.09s和0.56s，且很明显前者的超调量小于后者.当参数发生改变，PI控制的速度响应的调整时间增加到0.64s，而实时参数可调的内模控制几乎不受影响.当受到干扰时，前者的速度响应会出现4.5%的波动和0.3s的回复稳态时间，而后者的只有0.1%和0.02s.

5 结论

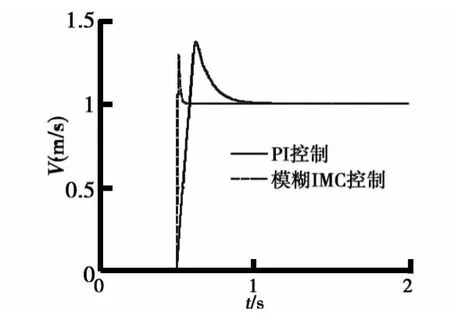
图5 情况1下的速度响应曲线

图6 情况2下的速度响应曲线

图7 情况3下的速度响应曲线

根据永磁同步电机在工作过程中的参数摄动和负载扰动等特点，结合内模原理和模糊控制的思想，设计出实时可调整参数的模糊内模控制器.在保证系统稳态性能的基础上，大幅度提高了系统的快速性和鲁棒性.通过仿真可观察到，相比于传统的PI控制，实时可调整参数的模糊内模控制对系统的速度响应较快且调整时间较短，能降低系统对于电机参数、负载扰动的敏感程度，具有较好的快速性、稳定性和鲁棒性.

［1］ 郭庆鼎，王成元，周美文，等.直线交流伺服系统的精密控制技术［M］.北京：机械工业出版社，2000.

［2］ 杨大磊，党选举，王占军.永磁直线同步电机的鲁棒自适应神经网络控制［J］.电气传动，2011，41（11）：54－57.

［3］ 徐月同，傅建中，陈子辰.永磁直线同步电机进给系统 H∞控制策略的研究［J］.浙江大学学报：工学版，2005，39（6）：789－794.

［4］ 陈伯时.电力拖动自动控制系统－运动控制系统［M］.北京：机械工业出版社，2003.

［5］ 陆华才，王军，田丽.永磁直线同步电机自适应内模控制研究［J］.安徽工程科技学院学报，2010，25（1）：25－27.

［6］ Yi Cui.Application of internal model control algorithm to pH process［D］.USA：University of Nevada Reno，2002.

［7］ 赵志诚，贾彦斌，张井岗.交流伺服模糊内模PID控制器设计［J］.火力与指挥控制，2008，33（11）：145－151.

［8］ 许力.智能控制与智能系统［M］.北京：机械工业出版社，2006.